MATERIALES ORTOTROPICOS
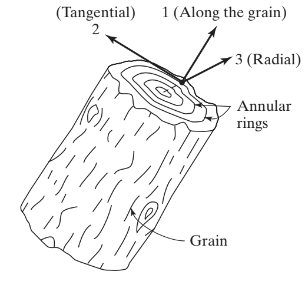
Antes de pasar por una explicación de las placas ortotrópicas, veamos algunos ejemplos de materiales ortotrópicos. Los materiales como los cristales de topacio y barita son ortotrópicos. (chandrapatla, 2012). Otro material ortotrópico muy común es la madera.. Figura 1 muestra los ejes principales en los que se definen las propiedades mecánicas de la madera.
Figura 1. La madera como material ortótropo (chandrapatla & Belegundu ,2012, página de referencia 233)
Eje 1 se define a lo largo del grano o fibras; eje 2 es tangencial y eje 3 corre radialmente. La ley de Hooke generalizada para este ejemplo (y para cualquier otro material ortótropo) Se puede escribir como
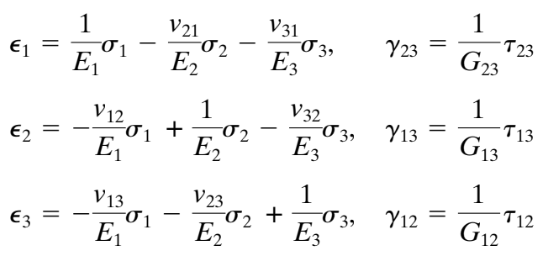
Ecuaciones 1. Ley de Hooke generalizada (chandrapatla & Belegundu,2012, página de referencia 233)
Dónde:
- mi1, mi2, mi3 son las cepas normales.
- C12, C13, C23 son las deformaciones cortantes.
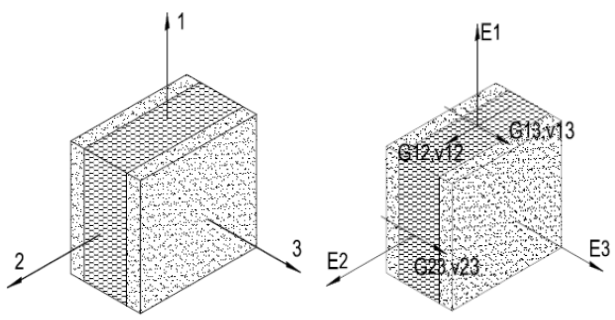
- E1, E2, y E3 son el módulo de Young a lo largo del eje principal.
- GRAMO12, GRAMO13, GRAMO23 son el módulo de corte.
- norte21, norte31, norte12, norte32, norte23 son las razones de Poisson.
- Para índices combinados, el primer número indica dónde se aplica la tensión y el segundo dónde se produce la deformación.
Por lo tanto, la principal diferencia en un material ortotrópico es que tenemos diferentes propiedades mecánicas a lo largo de los ejes principales, es decir, “x”, “y”, “z”.
PLACAS ORTOTROPICAS
Hay algunos casos de uso comunes para placas en ingeniería estructural, que podemos resumir de la siguiente manera: plano isotrópico, compuesto o sándwich y endurecido (W.Jiang et al, 1997).
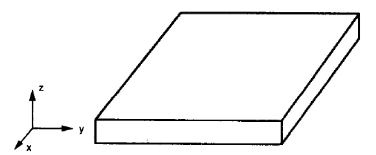
Las placas planas isotrópicas son placas regulares. (figura no.2), solo es necesario definir un valor uno para la relación de Poisson, Joven, y módulo de corte porque las propiedades mecánicas en cualquier dirección no cambian.
Figura no.2. Las placas planas son comúnmente isotrópicas. (W.Jiang et al, 1997, página de referencia 106)
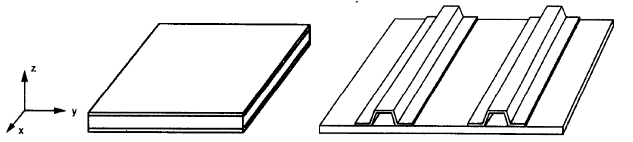
Para las dos últimas opciones, sándwich y placas rígidas (figura no.3), tenemos que definir diferentes propiedades mecánicas en su eje principal. Estos diferentes valores hacen que las placas sean ortotrópicas..
Figura 3. secciones (izquierda) y placas reforzadas con sombrero (verdad) (W.Jiang et al, 1997, página de referencia 106)
En una placa ortótropa, tendríamos dos ejes con la misma rigidez, figura no.3. Los ejes "x" e "y" se encuentran en un plano, y "z" es perpendicular a ella.
Podemos decir eso (W.Jiang et al, 1997):
- Ex = Ey ≠ Ez ; (Ex, Ey )> Ez .
- nortexz = norteyz ≠ nortexy ; (nortexz, norteyz) >nortexy
- GRAMOxy = GRAMOxz = GRAMOyz
Las expresiones indicadas anteriormente implican que las rigideces en las direcciones “x” e “y” son mayores que en “z”. Las relaciones de Poisson también muestran que hay más deformación en los planos relacionados con la dirección "z" que en un plano formado por los ejes "x" e "y"..
EJEMPLO
Descripción y configuración
Para resumir los conceptos aprendidos en las secciones anteriores, vamos a desarrollar un ejemplo en SkyCiv. Consiste en el análisis de un panel sándwich muro/losa construido con dos capas de hormigón proyectado separadas por un núcleo de poliestireno. Hemos elegido la siguiente referencia para las propiedades mecánicas que se utilizará en el modelado.: Torres Villavicencio et al. (2013).

Figura 4. Panel sándwich de pared/losa
Para capturar la diferencia de análisis en placas cuando seleccionamos las opciones avanzadas (ortotrópico), desarrollamos una breve comparación del panel sándwich descrito anteriormente y una aproximación en sus propiedades mecánicas usando un enfoque isotrópico. El último caso utiliza valores en propiedades mecánicas que no cambian a lo largo de sus ejes principales..
El objetivo de este ejemplo es comparar los resultados en términos de desplazamiento vertical. La configuración del modelo se muestra en la Figura 5.
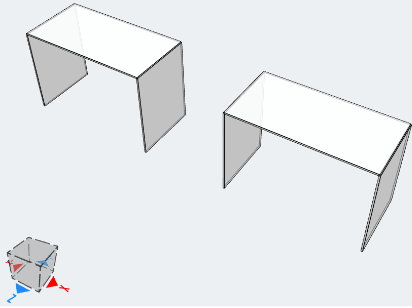 Figura 5. Configuración del modelo. ortotrópico (izquierda), Isotrópico (verdad)
Figura 5. Configuración del modelo. ortotrópico (izquierda), Isotrópico (verdad)
Propiedades mecánicas
Basado en diferentes informes de pruebas de laboratorio., las propiedades ortótropas del panel son (Torres Villavicencio et al, 2013):
| Propiedad | Valor |
|---|---|
| E1 (MPa) | 5613 |
| E2 (MPa) | 5613 |
| E3 (MPa) | 2807 |
| GRAMO12 (MPa) | 2245 |
| GRAMO23 (MPa) | 1123 |
| GRAMO13 (MPa) | 1123 |
| norte12 | 0.2 |
| norte23 | 0.25 |
| norte13 | 0.25 |
Cuadro nº 1. Propiedades mecánicas ortotrópicas del panel sándwich
Figura no.6. Ejes principales en elemento panel (Torres Villavicencio et al, 2013).
La aproximación para el caso isotrópico se indica en la siguiente tabla.
| Propiedad | Valor |
|---|---|
| E (MPa) | 5613 |
| GRAMO (MPa) | 2245 |
| norte | 0.20 |
Cuadro nº2. Aproximación de las propiedades mecánicas isotrópicas del panel sándwich
Modelado en SkyCiv
Ahora describimos de manera muy concisa los pasos necesarios para modelar el ejemplo.. (Para más detalles en el modelado de placas, consultar este enlace Modelado de placas SkyCiv). No he probado SkyCiv, seguir usando Structural 3D, simplemente Regístrate gratis aquí.
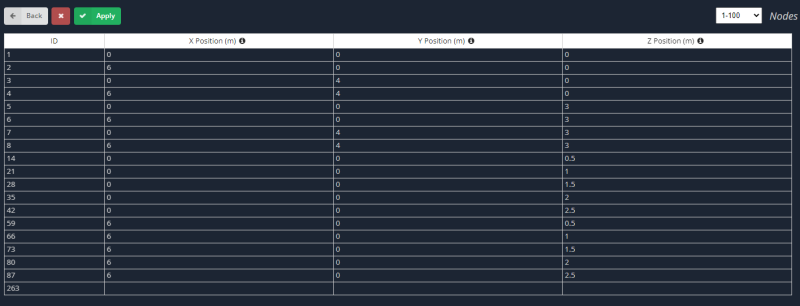
- Nodos: Para crear ambos casos, primero definimos los nodos correspondientes a las placas horizontal y vertical.

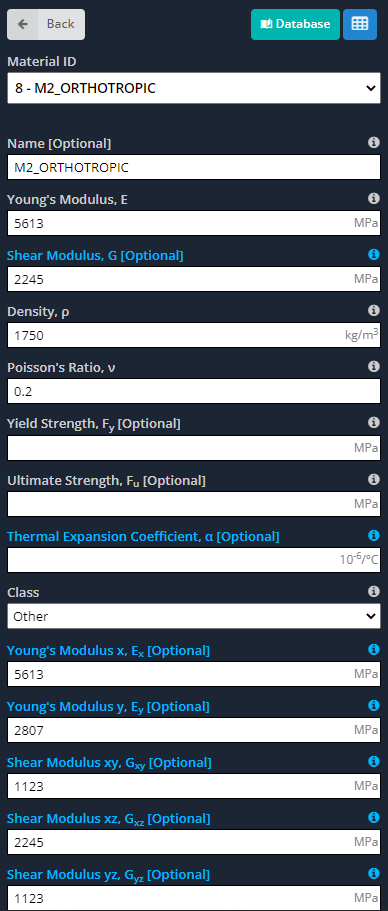
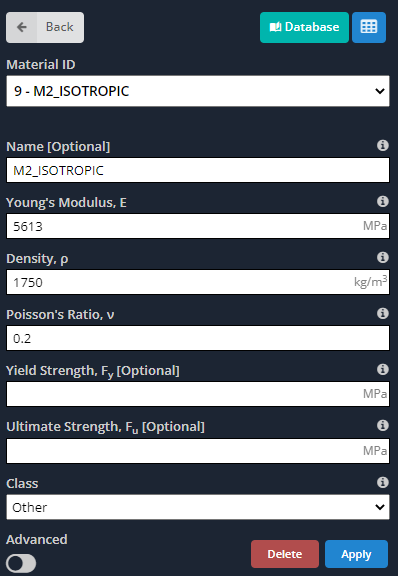
- Materiales: Como dijimos antes, Los materiales ortotrópicos tienen diferentes propiedades a lo largo de sus ejes principales.. Las siguientes imágenes indican las entradas que tenemos que definir para el modelo..


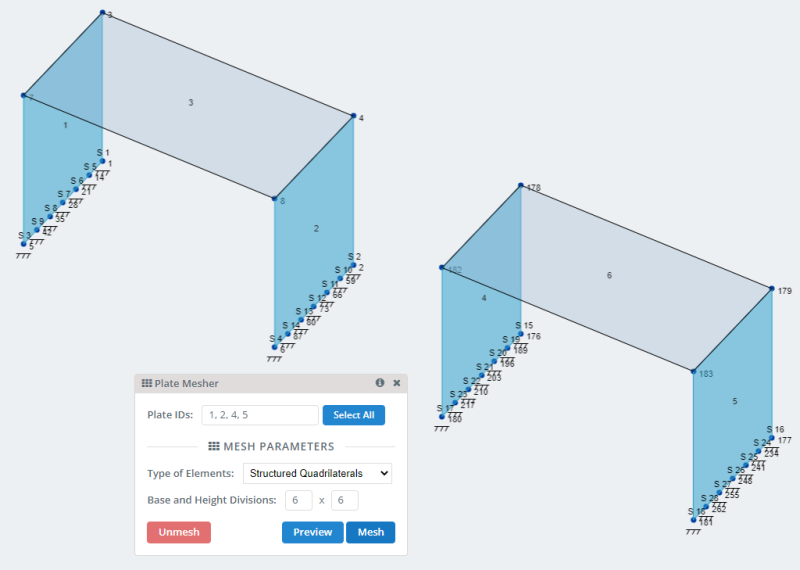
- Placas: A través de los nodos del modelo creamos las placas rectangulares.. Dos para el modelado de muros verticales y uno para el piso o losa.

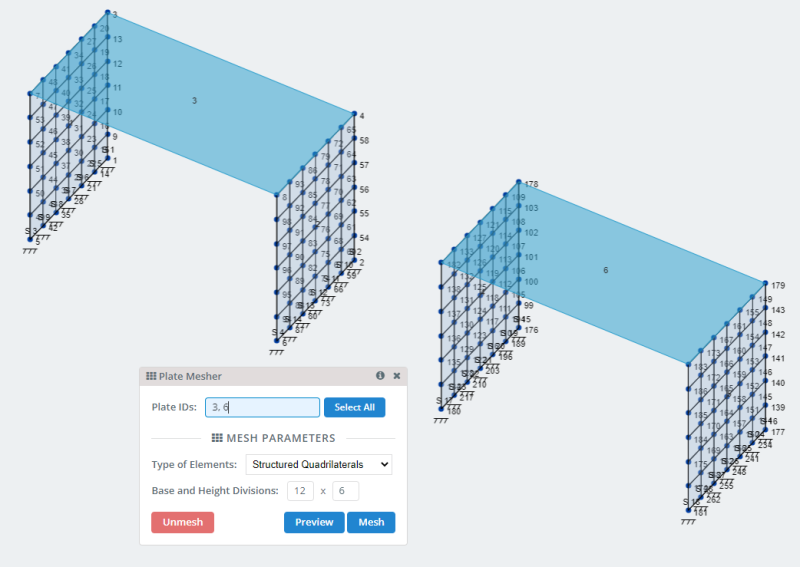
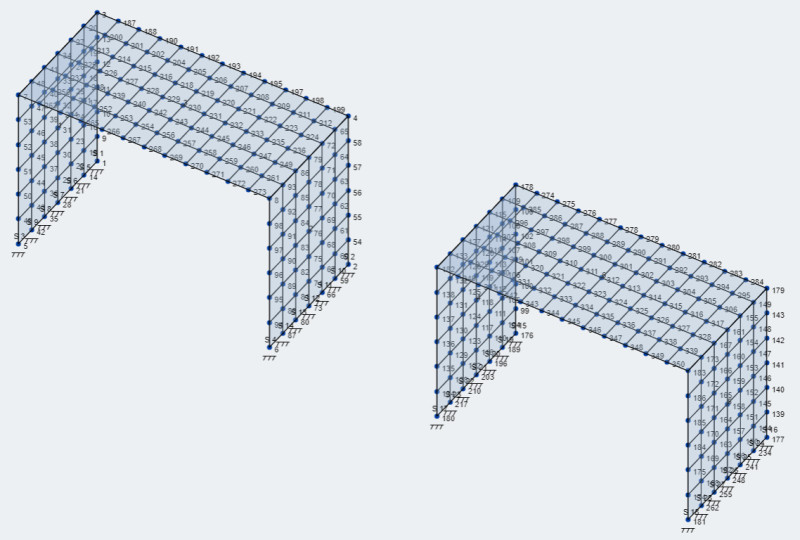
- Placas de malla: SkyCiv tiene muchas opciones para mallar placas y se puede consultar en Enredando tu plato . Para nuestro modelo usemos la opción de malla de cuadriláteros estructurados.



- Definición del caso de carga de peso propio: Solo consideraremos esta carga de peso propio para capturar el comportamiento estructural general de la placa..

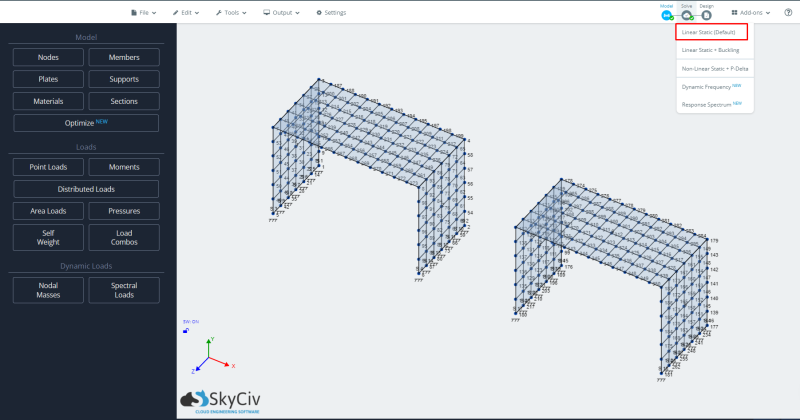
- Análisis de ejecución: Para ejecutar el modelo seleccionaremos el caso de análisis estático lineal.

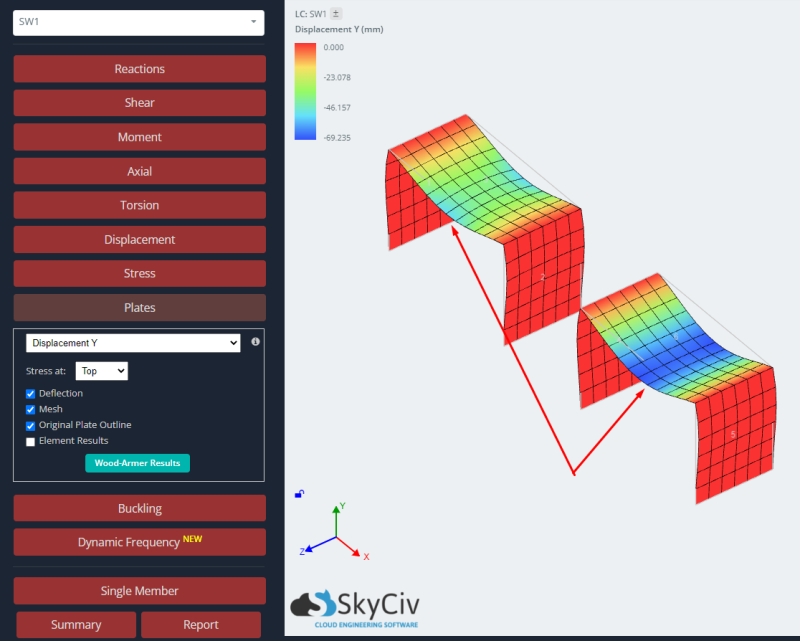
- Resultados: Finalmente, en este punto estudiamos la respuesta estructural para ambas placas, el caso isotrópico y ortotrópico. Para obtener más detalles sobre la lectura de resultados para el análisis de placas, puedes mirar este articulo Resultados del análisis de placa.

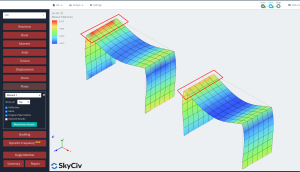
Estudiar la respuesta de ambos casos., comparamos los resultados del desplazamiento vertical y el momento flector. La placa ortotrópica muestra deflexiones más pequeñas y momentos de flexión más grandes que el caso isotrópico.. Podemos decir que el uso de un enfoque ortotrópico nos dará un elemento más rígido y esto afectará los resultados globales y locales en un análisis lineal elástico..
Empiece gratis
Vea SkyCiv Structural 3D gratis hoy para probar nuestro software!
Referencias:
- chandrapatla, Tirupathi R & Belegundu, Ashok (2012). “Introducción a los Elementos Finitos en Ingeniería” 4ª edición, educación Pearson.
- W. Jiang et al. (1997). “Modelado de elementos finitos de placas ortotrópicas rigidizadas y no rigidizadas”, Ordenadores & Estructuras Vol.63, No.1, páginas. 105-117, Elsevier Science Ltd.
- Torres Villavicencio et al (2013). “Trabajo monográfico: Ayudas de Diseño para Sistemas Portantes EMMEDUE de Paneles de Hormigón Armado con Núcleo de E.P.S (Sistema de Poliestireno Expandido)”. Universidad Nacional de Ingeniería.
- Todas las imágenes de software tomadas de Software de análisis estructural 3D SkyCiv