Descripción general
SkyCiv tiene un módulo robusto y avanzado para el diseño de losas de hormigón armado. Para acceder a esta función, primero debe haber construido un modelo en SkyCiv S3D y luego llamar al módulo para el cálculo automático con diferentes códigos de construcción como ACI-318, Estándares europeos y australianos, y así. El propósito principal del módulo para el diseño de placas es proporcionar la cantidad de barras de refuerzo de acero a lo largo de la placa..
Figura 1. Módulo de diseño de losa SkyCiv
Si eres nuevo en SkyCiv, Regístrese y pruebe el software usted mismo!
La documentación de SkyCiv proporciona un contenido excelente., incluyendo ejemplos y casos de análisis, tanto para aprender si eres nuevo en los módulos como para comparar los resultados del módulo de diseño de placas con cálculos manuales. No dude en consultar nuestros ejemplos de diseño según ACI-318, Eurocódigo, y AS3600.
Le sugerimos que lea este artículo antes de analizar en profundidad los sistemas de losas complejas. aquí, aprenderá cómo difieren los momentos de flexión según las dimensiones del plano de la losa. Hay dos casos de estudio., losas unidireccionales y bidireccionales. Entonces, empecemos a leer!
Comportamiento de losa en una dirección versus en dos direcciones
Consideremos el ejemplo de losa en la siguiente imagen, donde hay apoyo en cada borde de losa, y establecemos que esta se comportará como una placa de dos vías, es decir, que tiene un momento flector en las dos direcciones principales del plano.
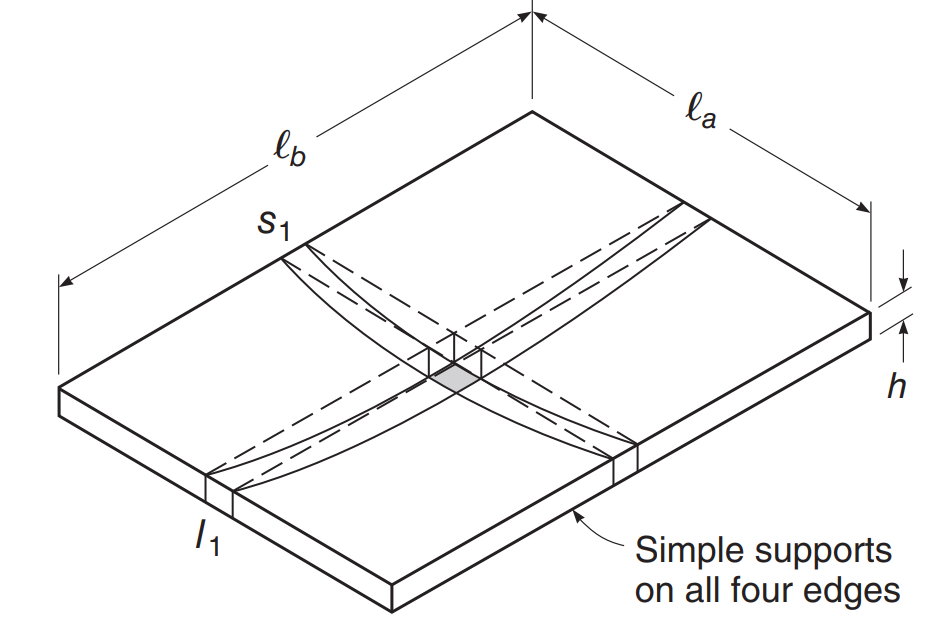
Figura 2. Ejemplo simple de losa en dos direcciones al doblar. (david darwin, Charles W. Dolan, arturo h. Nilson, “Diseño de Estructuras de Hormigón,” Decimoquinta edición, Educación McGraw-Hill)
Podemos definir el desplazamiento vertical como (\(la < l_b \)):
\(\Delta_a = frac{{5}{Washington}{l_a^4}}{384{E}{I}}\)
\(\Delta_b = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
Debido a que la losa es un sistema continuo, ambas deflexiones verticales tendrán el mismo valor. Podemos comparar las ecuaciones para expresar una relación entre la carga que lleva cada dirección en función de las dimensiones del plano.
\(\Delta_a = Delta_b to frac{{5}{Washington}{l_a^4}}{384{E}{I}} = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
\(\frac{Washington}{w_b} = {(\frac{l_b}{la}})^ 4 \)
Todas las referencias de hormigón armado para el diseño de losas se dividen en unidireccionales y bidireccionales si el cociente de \(\frac{l_b}{la}\) es mayor o menor que un valor de 2, respectivamente.
Usando las ecuaciones anteriores, Cuándo \(\frac{l_b}{la}=2), la carga transportada por la dirección corta es igual a \(w_a = {16}{w_b}\) y cuando el valor es \(\frac{l_b}{la}=1), la carga se distribuye por igual en ambas direcciones \(w_a ={w_b}\).
Momentos de losas en una dirección
Entonces, podemos ver que cuando el cociente de dimensiones es mayor que 2, prácticamente, todas las cargas y momentos de flexión se concentrarán solo en la dirección corta. Este caso es el comportamiento de losa unidireccional, y el momento flector máximo se puede obtener como una viga simplemente apoyada de ancho unitario.
\(METRO_{max,1,re}= frac{{Washington}{1 m}{l_a^2}}{8}\)
Momentos de losas en dos direcciones
La solución del caso de la losa en dos direcciones es un problema complejo y desafiante en mecánica estructural. Puede ver en la figura a continuación que el análisis general consiste en una placa con fuerzas y momentos completos en cada dirección..
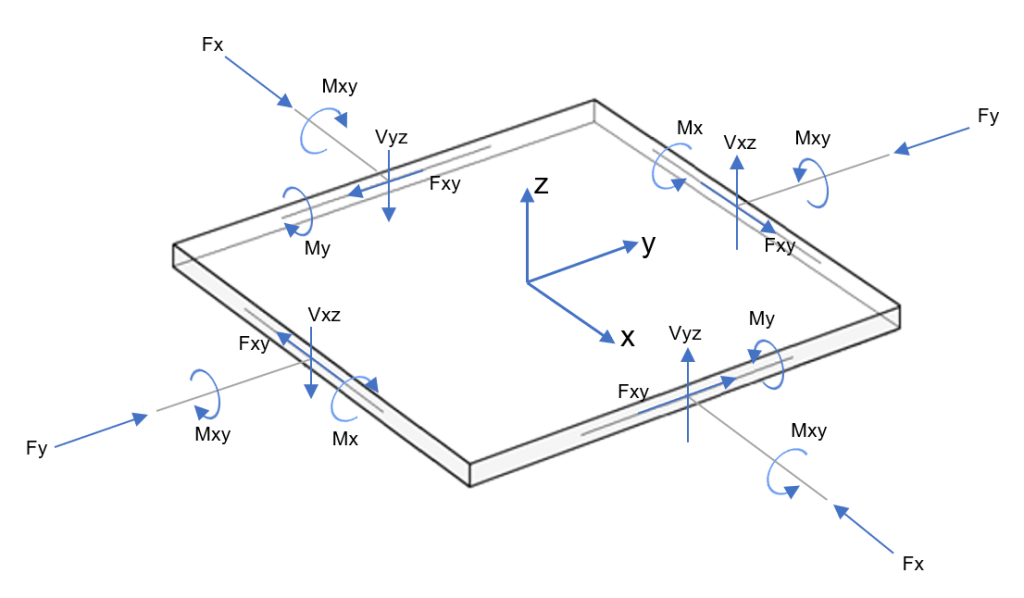
Figura 3. Acciones sobre elemento placa (momentos de flexión y torsión; fuerzas normales y cortantes)
Esta dificultad proviene del problema real a resolver es una ecuación diferencial parcial de cuarto orden que involucra la flexión en dos direcciones. La forma de esta ecuación es:
\(\frac{\parcial^4{w}}{{\parcial}{x^4}} + {2}\frac{{\parcial^4}{w}}{{{\parcial}{x^2}}{{\parcial}{y^2}}}+\frac{\parcial^4{w}}{{\parcial}{x^4}}-\frac{f_z}{re} = 0\)
Donde la rigidez de la placa (utilizando las propiedades mecánicas y geométricas elásticas) es \(D=frac{{E}{t ^ 3}}{{12}{(1-\no^2)}}\).
La solución analítica de esta ecuación solo está disponible para condiciones de apoyo sencillas.. La única forma de obtener una posible solución para casos reales y prácticos es a través de métodos numéricos como el Método de Elementos Finitos..
SkyCiv utiliza este enfoque para resolver el análisis de placas. En los siguientes enlaces, tendrás acceso a tutoriales para conocer las características de la plataforma SkyCiv: Diseño de Placas en S3D y Como modelar placas? .
Si eres nuevo en SkyCiv, Regístrese y pruebe el software usted mismo!

