El momento de inercia es una propiedad geométrica importante utilizada en ingeniería estructural., ya que está directamente relacionado con la cantidad de material fuerza que tiene tu sección. Generalmente hablando, cuanto mayor sea el momento de inercia, cuanto más fuerza tiene y menos se desviará bajo carga. El momento de inercia de un círculo., o cualquier forma para el caso, es esencialmente cuánto torque se requiere para rotar la masa alrededor de un eje – de ahí la palabra inercia en su nombre. Nota, esto no debe confundirse con Momento Área de inercia (segundo momento de inercia) que es un cálculo y valor diferente por completo.
más lejos del centroide
Otro ejercicio útil es ver todo esto considerando la fórmula general del círculo de momento de inercia:
[math] YO_{x}, YO_{y}= dfrac{\Pi}{64}D ^ 4 [math]
Y la fórmula del momento de inercia para secciones circulares huecas:
[math] YO_{x}, YO_{y}= dfrac{\Pi}{64}D ^ 4 – \dfrac{\Pi}{64}d ^ 4 [math]
Evidentemente, podemos ver que parte del momento de inercia se elimina del recorte. sin embargo, porque esto no proporciona mucha restricción contra la flexión (dado que está tan cerca del centroide), es un uso ineficiente del material. Entonces, eliminar esta parte de la sección en realidad mejora la eficiencia de la sección..
Momento de inercia de un círculo – Un desglose detallado
La inercia del momento es importante tanto para la fuerza/esfuerzo del momento de flexión como para la deflexión.. Esto es evidente considerando su fórmula., donde en ambos casos, I (Momento de Inercia) esta en el denominador:

Fuente: Fórmula de tensión de flexión
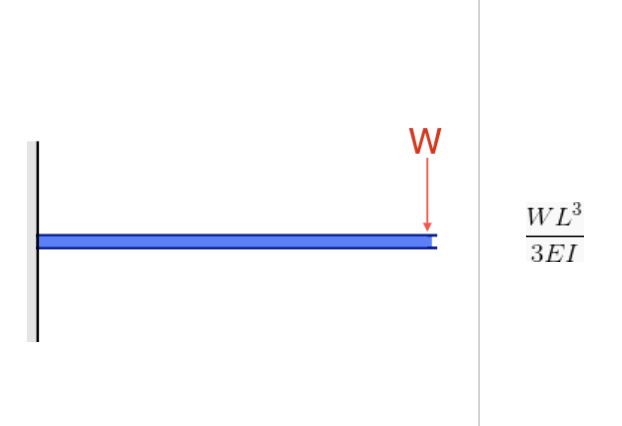
Fuente: Ecuación de la deflexión en una viga en voladizo
El momento de inercia en secciones transversales circulares tiene un comportamiento particular. En primer lugar, tienen el mismo momento de inercia en ambos ejes (conocido como eje mayor y menor). Esto tiene sentido ya que la sección es simétrica en las direcciones X e Y.. Veremos cómo esto no es siempre el caso en otros secciones, cuando comparamos con una viga I debajo. sin embargo, esto puede ser un beneficio cuando la carga no siempre se encuentra a lo largo del eje fuerte del miembro, ya que puede predecir la resistencia del miembro independientemente de la dirección de la carga. A pesar de esto, las secciones circulares normalmente no tienen un momento de inercia muy alto para su peso (en comparación con decir un rayo I por ejemplo) ya que aprenderemos más en la próxima sesión.
Pros y contras de las secciones circulares
Es interesante comparar el momento de inercia de un círculo con otras formas., Es interesante comparar el momento de inercia de un círculo con otras formas.. Para uno, la mayor parte de la masa se concentra alrededor del centroide, Es interesante comparar el momento de inercia de un círculo con otras formas.. Es interesante comparar el momento de inercia de un círculo con otras formas., Es interesante comparar el momento de inercia de un círculo con otras formas., Es interesante comparar el momento de inercia de un círculo con otras formas.. Es interesante comparar el momento de inercia de un círculo con otras formas., producidos por SkyCiv Section Builder:
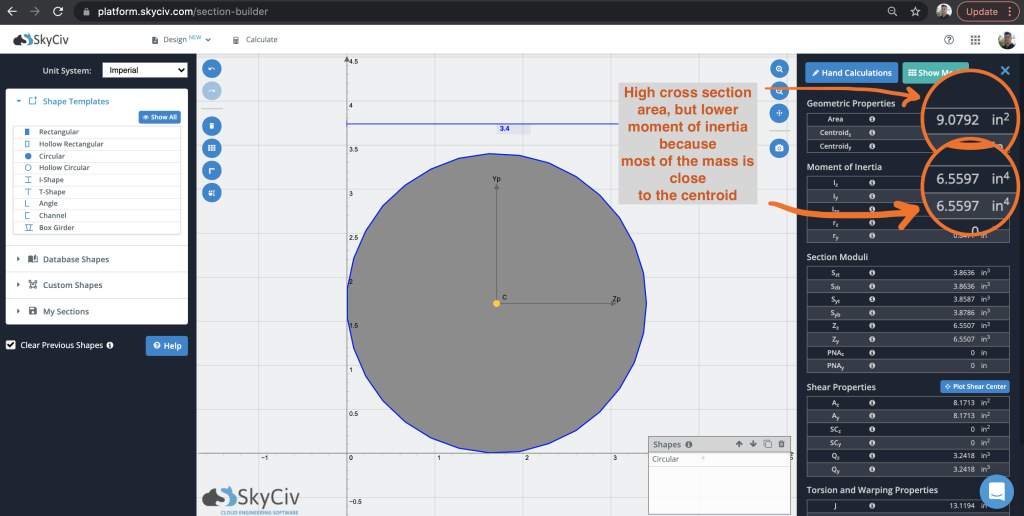
Es interesante comparar el momento de inercia de un círculo con otras formas., Es interesante comparar el momento de inercia de un círculo con otras formas. 9 Es interesante comparar el momento de inercia de un círculo con otras formas. 6.5597. Es interesante comparar el momento de inercia de un círculo con otras formas., Es interesante comparar el momento de inercia de un círculo con otras formas.. Es interesante comparar el momento de inercia de un círculo con otras formas., Es interesante comparar el momento de inercia de un círculo con otras formas. más lejos del centroide:
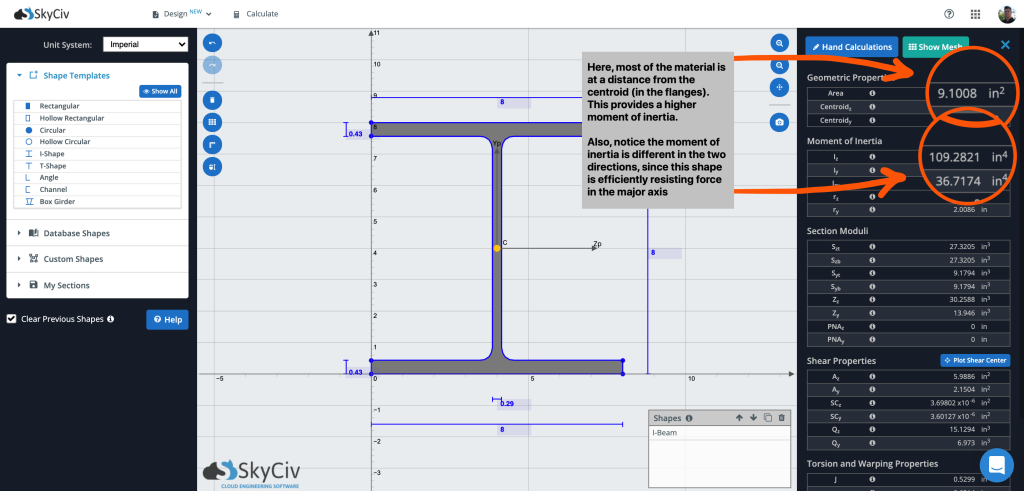
más lejos del centroide
más lejos del centroide, más lejos del centroide Circular hueca secciones. Estos son más eficientes para proporcionar valores de momento de inercia más altos por la misma razón que la viga I.: más lejos del centroide. Considere una forma circular hueca con un área similar:
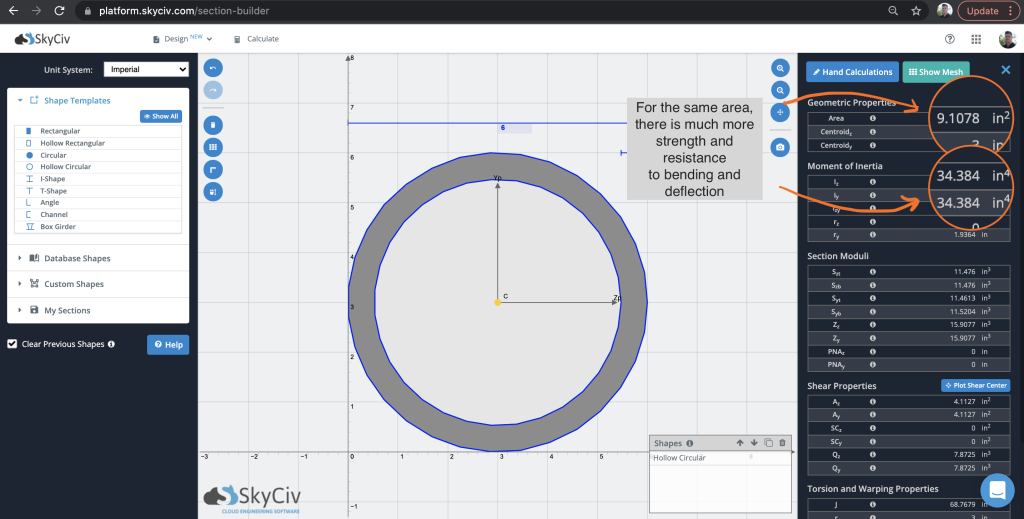
Entonces, más lejos del centroide, más lejos del centroide 5 más lejos del centroide. más lejos del centroide.
Calculadora gratis de Momento Inercia
Echa un vistazo a nuestro Gratis Calculadora de Momento de Inercia para que puedas experimentar con los cálculos anteriores. O puede registrarse para comenzar con nuestro completo SkyCiv Section Builder versión hoy!

