Un ejemplo de ASCE 7-16 cálculos de carga de viento (procedimiento direccional) para un edificio en forma de L

En este artículo, un ejemplo de cálculo de la presión de la carga del viento para un edificio en forma de L en Córdoba, Se mostrará Tennessee. Este cálculo estará de acuerdo con ASCE 7-16 cálculos de carga de viento (procedimiento direccional).

Para este estudio de caso, los datos de estructura son los siguientes:

Ubicación	Cordova, Memphis, Tennesse Elevación + 110.0m
Ocupación	Miscelánea – Estructura de la planta
Terreno	Campo plano
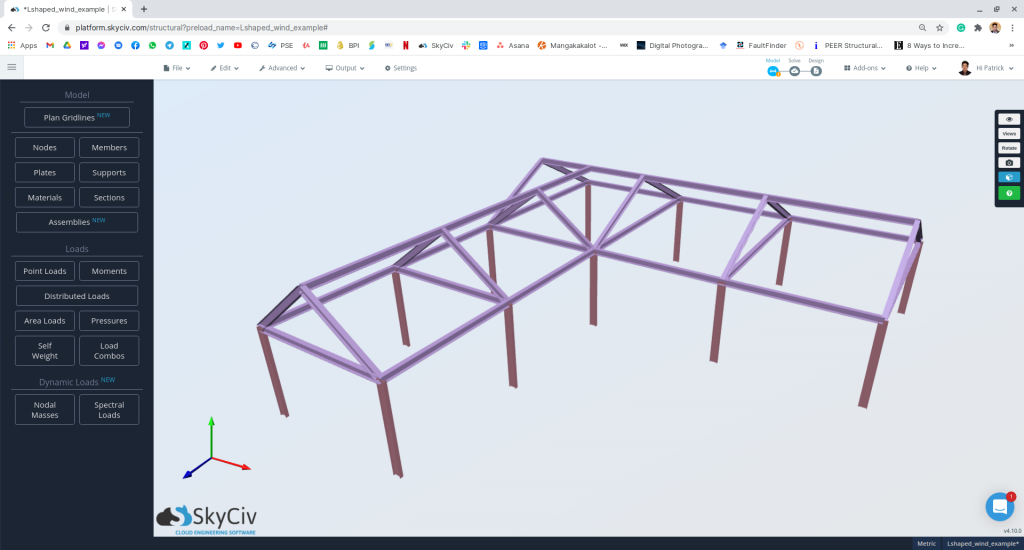
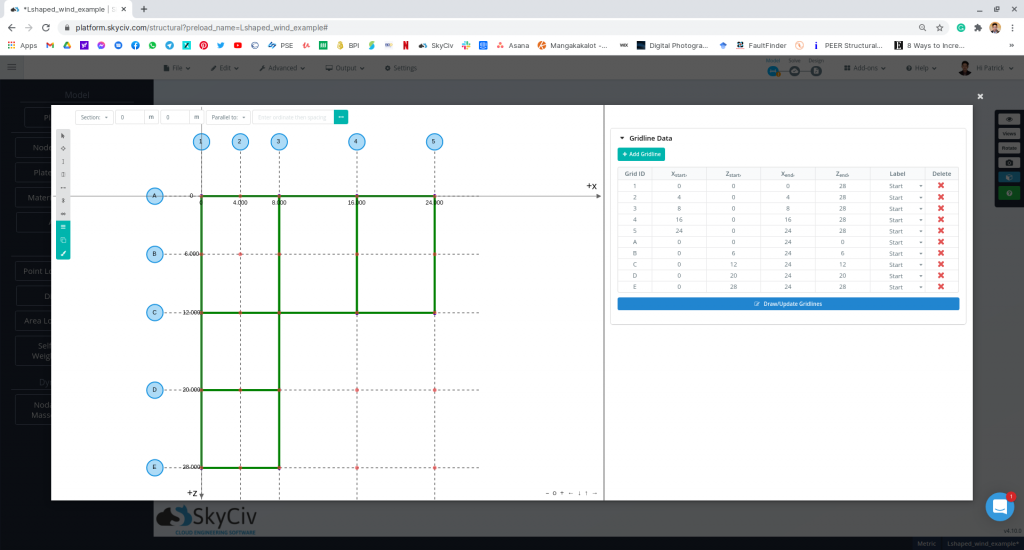
Dimensiones	28m (12m ancho) x 24m (8m ancho) en plan Altura del alero 5 m Altura del ápice. 8 m Inclinación del techo: 1:2 para marco principal (26.57°) 3:4 para extensión (36.87°) Con apertura

Un cálculo similar para una construcción de techo a dos aguas usando ASCE 7-10 (unidades imperiales) se hace referencia en este ejemplo y se puede acceder mediante este enlace. La fórmula para determinar la presión del viento de diseño son:

Para edificios cerrados y parcialmente cerrados:

\(p = qG{C}_ _{pag} -{q}_ _{i}({GC}_ _{pi})\) (1)

Para edificios abiertos:

\(p = q{G}_ _{F}{C}_ _{pag} -{q}({GC}_ _{pi})\) (2)

Dónde:

\(GRAMO) = Factor de efecto de ráfaga
\({C}_ _{pag}\) = coeficiente de presión externa
\(({GC}_ _{pi})\)= Coeficiente de presión interna
\(q ) = Presión de velocidad, en pa, dada por la fórmula:

\(q = 0.613{K}_ _{z}{K}_ _{zt}{K}_ _{d}V ^ 2 ) (3)

\(q ) = \({q}_ _{h}\) para paredes sotavento, paredes laterales, y techos,evaluado a la altura media del techo, \(h )
\(q ) = \({q}_ _{z}\) para muros de barlovento, evaluado en altura, \(desde)
\({q}_ _{i}\) = \({q}_ _{h}\) para la evaluación de presión interna negativa, \((-{GC}_ _{pi})\) evaluación y \({q}_ _{z}\) para la evaluación de presión interna positiva \((+{GC}_ _{pi})\) de edificios parcialmente cerrados, pero puede tomarse como \({q}_ _{h}\) para un valor conservador.
\({K}_ _{z}\) = coeficiente de presión de velocidad
\({K}_ _{zt}\)= factor topográfico
\({K}_ _{d}\)= factor de direccionalidad del viento
\(V ) = velocidad básica del viento en m / s

Categoría de Riesgo

Lo primero para determinar las presiones del viento de diseño es clasificar la categoría de riesgo de la estructura., que se basa en el uso u ocupación de la estructura. Dado que este ejemplo es una estructura de planta, se clasifica como Categoría de riesgo IV. Ver Tabla 1.5-1 de ASCE 7-16 para obtener más información sobre la clasificación de categorías de riesgo.

Velocidad Básica del Viento, \(V )

En ASCE 7-16, los datos de velocidad del viento se pueden obtener de Cifras 26.5-1 a 26.5-2. Desde Figura 26.5-1A, Cordova, Memphis, Tennessee está cerca del punto rojo que se muestra en la Figura 3 a continuación, y posteriormente, la velocidad básica del viento, \(V ), es 52 em. Tenga en cuenta que los valores deben interpolarse entre contornos de viento conocidos.

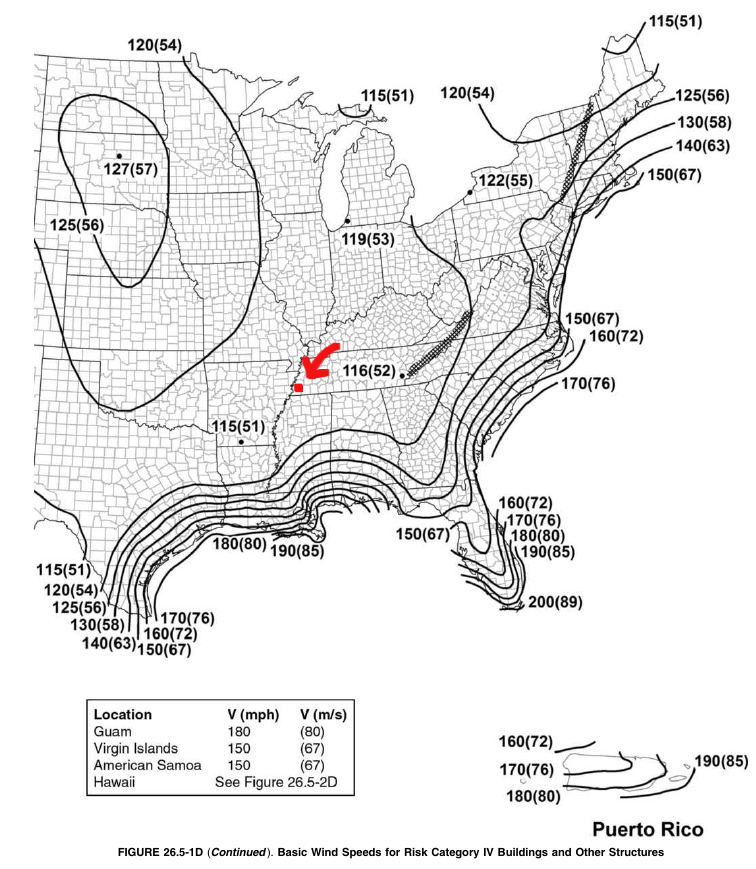
SkyCiv puede automatizar los cálculos de la velocidad del viento usando solo unos pocos parámetros. Pruebe nuestro herramienta gratuita de viento de SkyCiv.

Calculadora de carga de viento SkyCiv

Categoría de Exposición

Ver Sección de 26.7 de ASCE 7-16 detalla el procedimiento para determinar la categoría de exposición.

Dependiendo de la dirección del viento seleccionada, la exposición de la estructura se determinará a partir del sector de 45° a barlovento. La exposición que se debe adoptar será aquella que genere la mayor carga de viento desde dicha dirección. La descripción de cada clasificación de exposición se detalla en las Secciones 26.7.2 y 26.7.3 de ASCE 7-16.

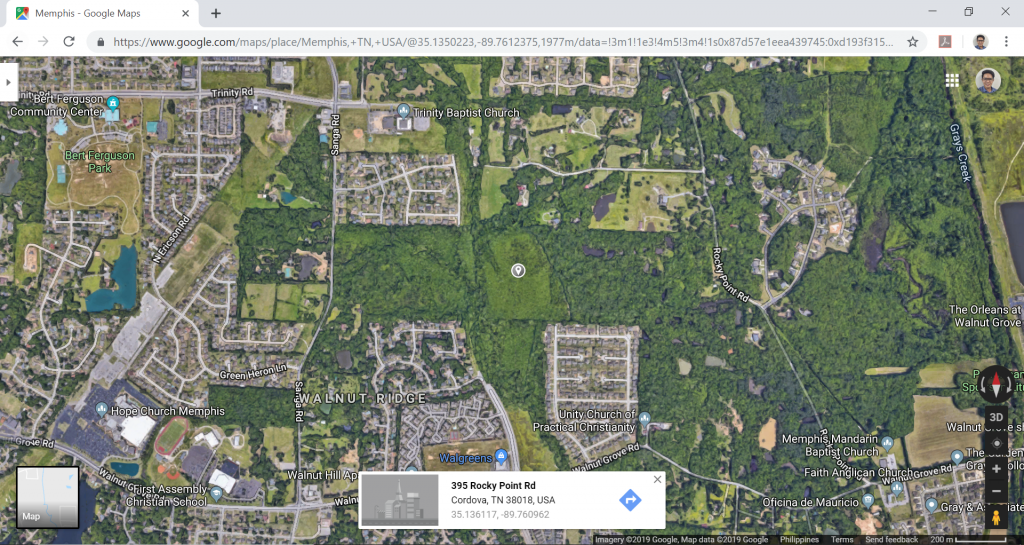
Para nuestro ejemplo, ya que la ubicación de la estructura está en tierras de cultivo en Córdoba, Memphis, Tennesse, sin edificios que superen los 30 ft, de altura, el área se clasifica como Exposición C. Una herramienta útil para determinar la categoría de exposición es ver el sitio potencial a través de una imagen satelital (como Google Maps, por ejemplo).

Factor de Direccionalidad del Viento, \({K}_ _{d}\)

Los factores de direccionalidad del viento, \({K}_ _{d}\), para nuestra estructura son ambos iguales a 0.85 ya que el edificio es el principal sistema de resistencia a la fuerza del viento y también tiene componentes y revestimientos adheridos a la estructura. Esto se muestra en Tabla 26.6-1 de ASCE 7-16.

Factor Topográfico, \({K}_ _{zt}\)

Dado que la ubicación de la estructura es en una tierra de cultivo plana, podemos asumir que el factor topográfico, \({K}_ _{zt}\), es 1.0. De lo contrario, el factor se puede resolver usando Figura 26.8-1 de ASCE 7-16. Para determinar si se requieren más cálculos del factor topográfico, ver Sección de 26.8.1, si su sitio no cumple con todas las condiciones listadas, el factor topográfico se puede tomar como 1.0.

Nota: Los factores topográficos se pueden calcular automáticamente usando el Software de diseño de viento SkyCiv. Para obtener más información sobre el cálculo del factor topográfico, Mira esto artículo.

Factor de elevación del suelo, \({K}_ _{mi}\)

El factor de elevación del suelo, \({K}_ _{mi}\), se introduce en ASCE 7-16 considerar la variación en la densidad del aire basada en la elevación del suelo sobre el nivel medio del mar. Este factor se puede calcular usando:

\( {K}_ _{mi} = {mi}^{-0.000119{z}_ _{gramo}}\) (4)

Dónde:
\({z}_ _{gramo}\) es la elevación del suelo sobre el nivel medio del mar en metros

Por lo tanto, para este estudio de caso, ya que la elevación del suelo es de + 110,0 m, \({K}_ _{mi}\) es igual a 0.987.

Coeficiente de Presión de Velocidad, \({K}_ _{z}\)

El coeficiente de presión de velocidad, \({K}_ _{z}\), se puede calcular utilizando la Tabla 26.10-1 de ASCE 7-16. Este parámetro depende de la altura sobre el nivel del suelo en el punto donde se considera la presión del viento, y de la categoría de exposición. Además, los valores mostrados en la tabla se basan en la siguiente fórmula:

Por 4.6 m < \({z}\) < \({z}_ _{gramo}\): \({K}_ _{z} = 2.01(con/{z}_ _{gramo})^{2/una}\) (5)
Por \({z}\) < 4.6 m: \({K}_ _{z} = 2.01(4.6/{z}_ _{gramo})^{2/una}\) (6)

Dónde:

Exposición	una	\({z}_ _{gramo}\)(m)
Exposición B	7.0	365.76
Exposición C	9.5	274.32
Exposición D	11.5	213.36

Normalmente, los coeficientes de presión de velocidad a la altura media del techo, \({K}_ _{h}\), y en cada nivel de piso, \({K}_ _{día}\), son los valores que necesitamos para calcular las presiones de diseño del viento. En este ejemplo, dado que la presión del viento en el lado de barlovento tiene una naturaleza parabólica, podemos simplificar esta carga asumiendo que se aplica una presión uniforme en las paredes entre los niveles de los pisos. Podemos simplificar la presión de barlovento y dividirla en 2 niveles, a la altura del alero (+5.0m), y a la altura media del techo (+6.5m). Además, una = 9.5 y \({z}_ _{gramo}\) es igual a 274.32 m ya que la ubicación de la estructura se clasifica como Exposición C.

Elevación (m)	\( {K}_ _{z} \)
5 (altura del alero)	0.865
6.5 (altura media del techo)	0.914

Presión de Velocidad, \( q \)

A partir de la Ecuación (3), podemos resolver la presión de velocidad, \( q \) en pa, para cada elevación considerada.

Elevación, m	\( {K}_ _{z} \)	\( {K}_ _{zt} \)	\( {K}_ _{d} \)	\( {K}_ _{mi} \)	\( V \), em	\( q \), Bien
5 (altura del alero)	0.865	1.0	0.85	0.987	52	1202.87
6.5 (altura media del techo)	0.914	1.0	0.85	0.987	52	\( {q}_ _{h} \) = 1271.01

Factor de Efecto de Ráfaga, \( G \)

El factor de efecto de ráfaga, \( G \), se establece en 0.85 ya que se asume que la estructura es rígida (Sección de 26.11 de ASCE 7-16).

Clasificación del Cerramiento y Coeficiente de Presión Interna, \( ({GC}_ _{pi}) \)

Se asume que la estructura de la planta tiene aberturas que satisfacen la definición de un edificio parcialmente cerrado in Sección de 26.2 de ASCE 7-16. Así, el coeficiente de presión interna, \( ({GC}_ _{pi}) \), será de +0.55 y -0.55 Residencia en Tabla 26.13-1 de ASCE 7-16. Por lo tanto:

\(+{pag}_ _{i} = {q}_ _{i}(+G{C}_ _{pi}) \) = (1271.01)(+0.55) = 699.06 Bien
\(-{pag}_ _{i} = {q}_ _{i}(-G{C}_ _{pi}) \) = (1271.01)(-0.55) = -699.06 Bien

 

Coeficiente de presión externa, \({C}_ _{pag}\)

Para edificios cerrados y parcialmente cerrados, el coeficiente de presión externa, \({C}_ _{pag}\), se calcula utilizando la información proporcionada en Figura 27.4-1 mediante Figura 27.4-3. Para un edificio parcialmente cerrado con techo a dos aguas, usar Figura 27.4-1. Los coeficientes de presión externa para las paredes y el techo se calculan por separado utilizando los parámetros de construcción L, B y h, que se definen en la Nota 7 de Figura 27.4-1.

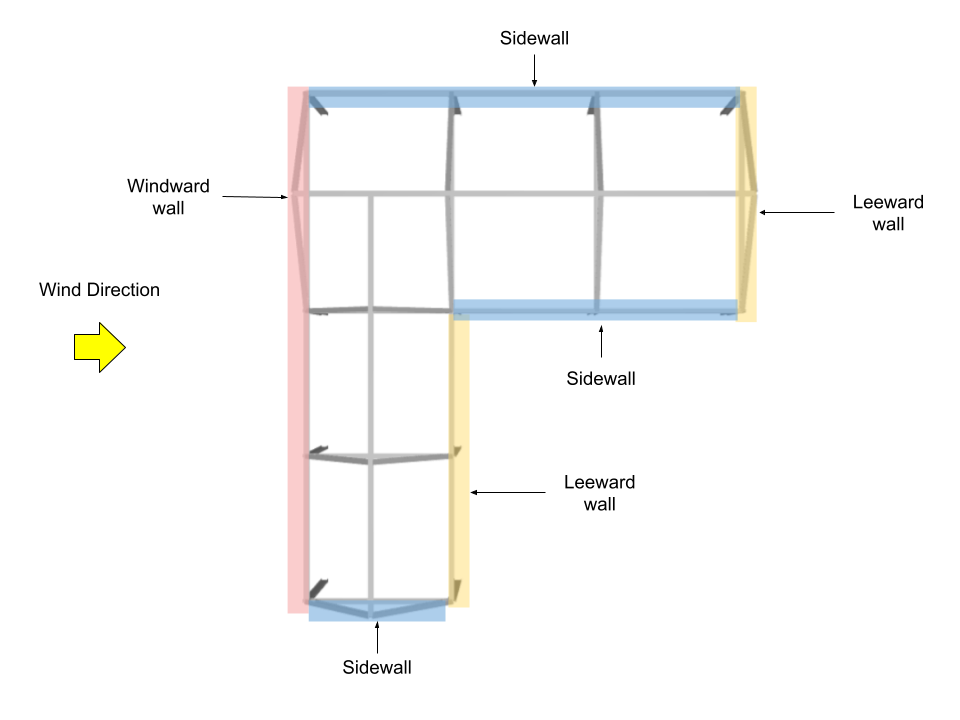
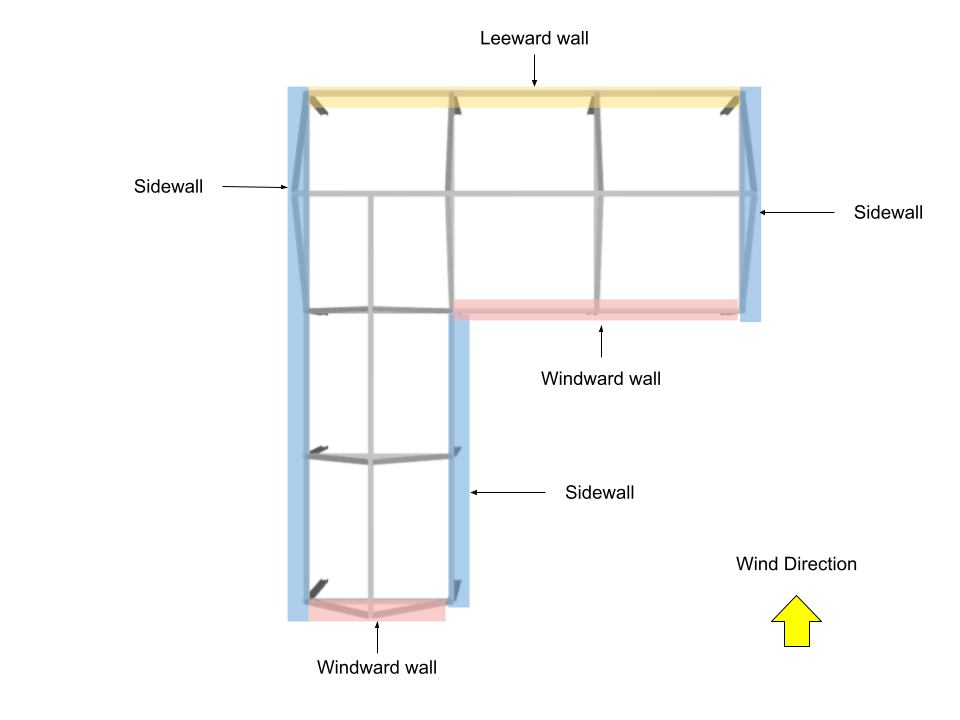
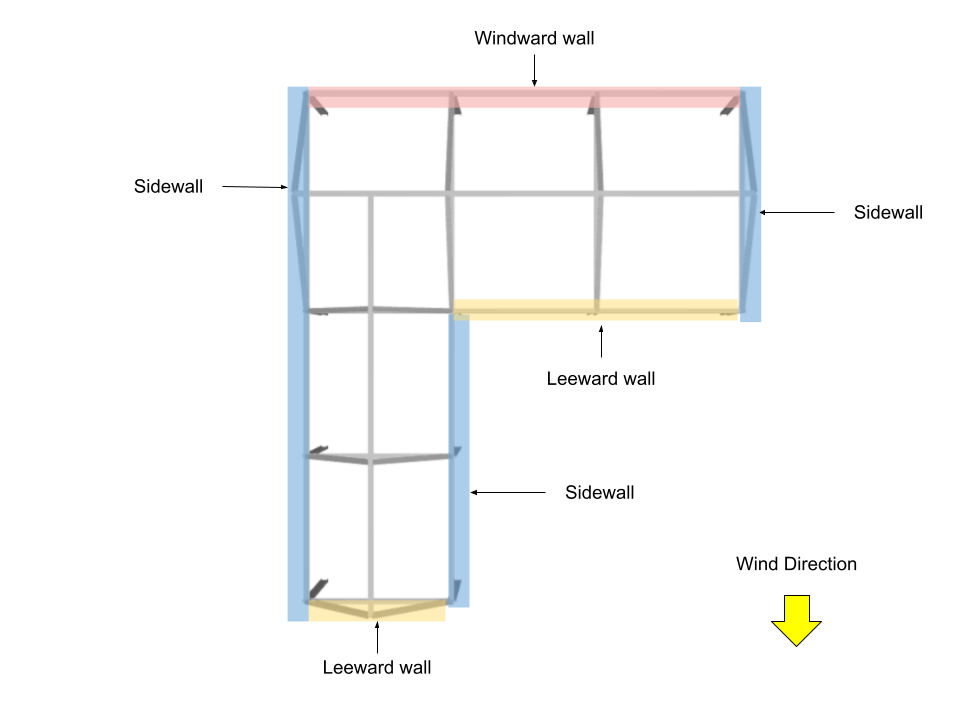
En este ejemplo, ya que la estructura es asimétrica, se considerarán cuatro direcciones del viento: dos (2) para dirección del viento paralela al lado de 24 m, y dos (2) para dirección del viento paralela al lado de 28 m.

Para dirección del viento paralela al lado de 24 m

Así, necesitamos calcular el L / B y h / L:

Altura media del techo, h = 6.5 m
Longitud del edificio, L = 24 m
Ancho de construcción, B = 28 m
L / B = 0.857
h / L = 0.271
h / B = 0.232

Coeficientes de presión de pared, \({C}_ _{pag}\), y presión externa, \({pag}_ _{mi}\)

.Para paredes, los coeficientes de presión externa se calculan a partir de la Figura 27.3-1 de ASCE 7-16 dónde \({q}_ _{h}\) = 1271.011 Bien y \( G \) = 0.85.

Superficie	h, m	Coeficientes de presión de pared, \({C}_ _{pag}\)	\({pag}_ _{mi}\), Bien
Muro de barlovento	5.0	0.8	817.953
	6.5	0.8	864.288
Muro de sotavento	6.5	-0.5	-540.180
Paredes laterales	6.5	-0.7	-756.252

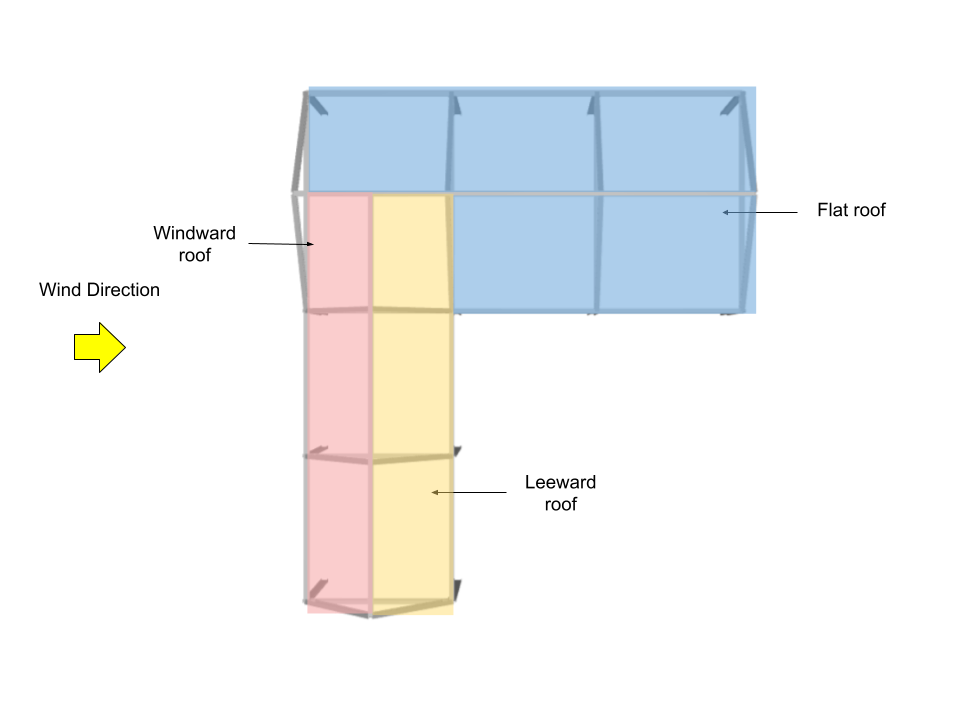
Coeficientes de presión del techo, \({C}_ _{pag}\), y presión externa, \({pag}_ _{mi}\)

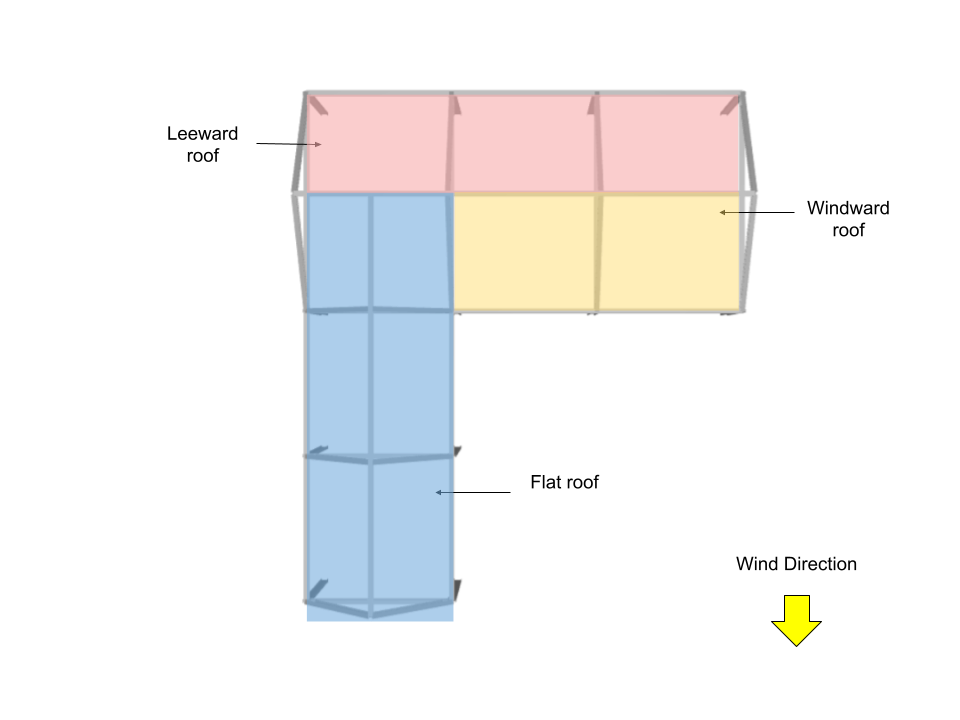
Para techo, los coeficientes de presión externa se calculan a partir de la Figura 27.3-1 de ASCE 7-16 dónde \({q}_ _{h}\) = 1271.011 Bien. Tenga en cuenta que para esta dirección del viento, presiones del techo de barlovento y sotavento (superficies del techo 1 y 2) se calculan usando θ = 36,87 ° y θ = 0 ° para superficies de techo 3 y 4.

Superficie	Ubicación	Coeficientes de presión del techo, \({C}_ _{pag}\)	\({pag}_ _{mi}\), Bien
Techo de barlovento	–	0.4	432.144
Techo de sotavento	–	-0.6	-648.216
Paralelo al viento (a lo largo de la cresta)	0 ah desde el borde	-0.9 -0.18	-972.324 -194.465
	ha 2 h desde el borde	-0.5 -0.18	-540.180 -194.465
	> 2h desde el borde	-0.3 -0.18	-324.108 -194.465

Por lo tanto, combinatorio \({pag}_ _{mi}\) y \({pag}_ _{i}\), se pueden obtener las presiones de diseño correspondientes:

Tipo	Superficie	Elevación / Ubicación, m	\({pag}_ _{mi}\), Bien	\({pag}_ _{mi}\) – +\({pag}_ _{i}\), Bien	\({pag}_ _{mi}\) – -\({pag}_ _{i}\), Bien
Paredes	Muro de barlovento	5.0	817.953	118.897	1517.009
		6.5	864.288	165.231	1563.344
	Muro de sotavento	–	-540.180	-1239.236	158.876
	Paredes laterales	–	-756.252	-1455.308	-57.196
Techo	Barlovento	–	432.144	-266.912	1131.200
	Sotavento	–	-648.216	-1347.272	50.840
	Departamento (a lo largo de la cresta)	0 a h	-972.324 -194.465	-1671.380 -893.521	-273.267 504.592
		ha 2 h	-540.180 -194.465	-1239.236 -893.521	158.876 504.592
		> 2h	-324.108 -194.465	-1023.164 -893.521	374.948 504.592

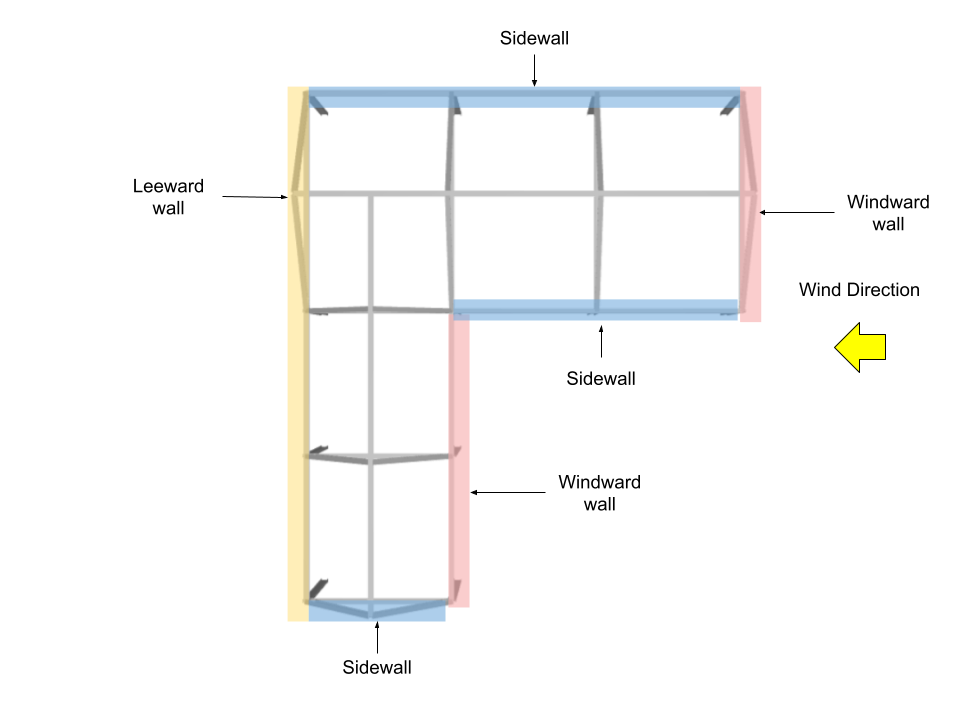
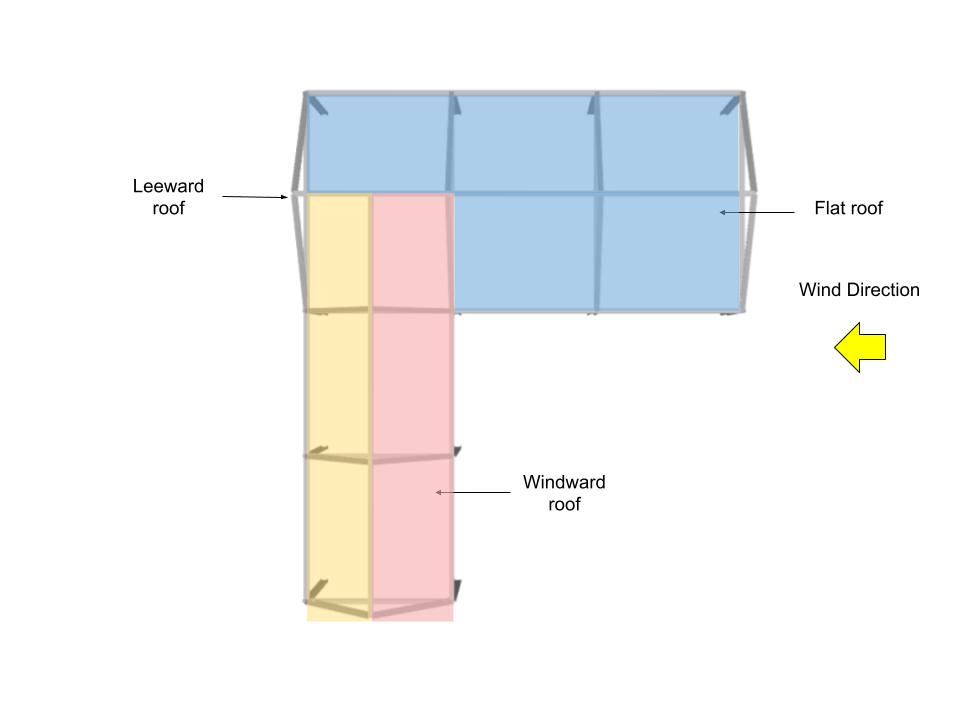
Para dirección del viento paralela al lado de 28 m

Así, necesitamos calcular el L / B y h / L:

Altura media del techo, h = 6.5 m
Longitud del edificio, L = 28 m
Ancho de construcción, B = 24 m
L / B = 0.857
h / L = 0.232
h / B = 0.271

Coeficientes de presión de pared, \({C}_ _{pag}\), y presión externa, \({pag}_ _{mi}\)

.Para presión de pared de diseño, los coeficientes de presión externa se calculan a partir de la Figura 27.3-1 de ASCE 7-16 dónde \({q}_ _{h}\) = 1271.011 Bien y \( G \) = 0.85.

Superficie	h, m	Coeficientes de presión de pared, \({C}_ _{pag}\)	\({pag}_ _{mi}\), Bien
Muro de barlovento	5.0	0.8	817.953
	6.5	0.8	864.288
Muro de sotavento	6.5	-0.467	-504.528
Paredes laterales	6.5	-0.7	-756.252

Coeficientes de presión del techo, \({C}_ _{pag}\), y presión externa, \({pag}_ _{mi}\)

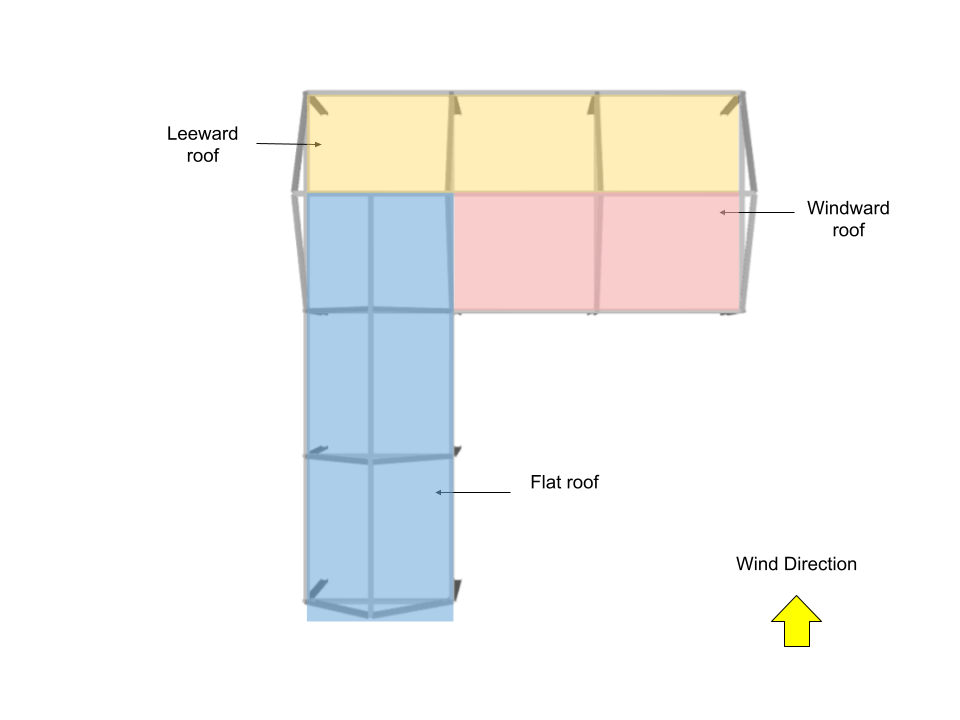
Para techo, los coeficientes de presión externa se calculan a partir de la Figura 27.3-1 de ASCE 7-16 dónde \({q}_ _{h}\) = 1271.011 Bien. Tenga en cuenta que para esta dirección del viento, presiones del techo de barlovento y sotavento (superficies del techo 3 y 4) se calculan usando θ = 26,57 ° y θ = 0 ° para superficies de techo 1 y 2.

Superficie	Ubicación	Coeficientes de presión del techo, \({C}_ _{pag}\)	\({pag}_ _{mi}\), Bien
Techo de barlovento	–	-0.2 0.3	-216.072 324.108
Techo de sotavento	–	-0.6	-648.216
Paralelo al viento (a lo largo de la cresta)	0 ah desde el borde	-0.9 -0.18	-972.324 -194.465
	ha 2 h desde el borde	-0.5 -0.18	-540.180 -194.465
	> 2h desde el borde	-0.3 -0.18	-324.108 -194.465

Por lo tanto, combinatorio \({pag}_ _{mi}\) y \({pag}_ _{i}\), se pueden obtener las presiones de diseño correspondientes:

Tipo	Superficie	Elevación / Ubicación, m	\({pag}_ _{mi}\), Bien	\({pag}_ _{mi}\) – +\({pag}_ _{i}\), Bien	\({pag}_ _{mi}\) – -\({pag}_ _{i}\), Bien
Paredes	Muro de barlovento	5.0	817.953	118.897	1517.009
		6.5	864.288	165.231	1563.344
	Muro de sotavento	–	-504.528	-1203.584	194.528
	Paredes laterales	–	-756.252	-1455.308	-57.196
Techo	Barlovento	–	-216.072 324.108	-915.128 -374.948	482.984 1023.164
	Sotavento	–	-648.216	-1347.272	50.840
	Departamento (a lo largo de la cresta)	0 a h	-972.324 -194.465	-1671.380 -893.521	-273.267 504.592
		ha 2 h	-540.180 -194.465	-1239.236 -893.521	158.876 504.592
		> 2h	-324.108 -194.465	-1023.164 -893.521	374.948 504.592

 

Referencias:

• Coulbourne, W. L., & Stafford, T. E. (2020, abril). Cargas de viento: Guía de las disposiciones de carga de viento de ASCE 7-16. Sociedad Americana de Ingenieros Civiles.
• Sociedad Americana de Ingenieros Civiles. (2017, junio). Cargas mínimas de diseño y criterios asociados para edificios y otras estructuras.. Sociedad Americana de Ingenieros Civiles.