Los fundamentos del centroide
Es importante tener en cuenta que en una sección transversal, cuya área es uniforme en todo, el centroide se puede encontrar tomando la suma de momentos con respecto a un eje establecido arbitrariamente, pero generalmente se coloca en la fibra superior o inferior. Consulte nuestro artículo anterior sobre cómo encontrar el centroide de una sección de viga y calculadora de centroide gratuita SkyCiv.
Fundamentalmente, el centroide puede obtenerse tomando la suma de momentos sobre la suma del área. Que se expresa de esta manera.
[math]
\bar{x}= frac{1}{A}\int xf left ( x right )dx
[math]

Resumen de ecuaciones centroides
En la ecuación anterior, F(x) es la función y x es el brazo de momento. Para ilustrar mejor esto, derivaremos el centroide y de un triángulo arbitrario con su base coincidente con el eje x. En esta situación, la forma del triángulo, ya sea equilátero, isósceles o escaleno es irrelevante ya que todo es relativo solo al eje x. Tenga en cuenta que la forma es irrelevante si la base del triángulo es coincidente o paralela con respecto al eje. Este no será el caso al resolver para el centroide x. En lugar, puedes imaginarlo obteniendo el centroide de dos triángulos rectángulos con respecto al eje y. Por conveniencia, imaginemos un triángulo isósceles similar a la tabla de referencia a continuación. Encontrar la relación entre b y h producirá la siguiente relación.
[math]
\frac{-y}{x}= frac{-h}{b}
[math]
Tenga en cuenta que la pendiente es negativa ya que estamos imaginando que el triángulo está en posición vertical. Si imaginamos que el triángulo se invierte, la pendiente sería positiva. Independientemente, la relación sigue siendo la misma. Como x = f(y), la relación anterior se puede reescribir de la siguiente manera.
[math]
x = f izquierda ( y right )= frac{b}{h}y
[math]
Ahora podemos resolver el centroide. Ajustando la primera ecuación anterior, obtenemos lo siguiente.
[math]
\bar{y}= frac{1}{A}\int yf left ( y right )dos
[math]
Conectar valores adicionales y sustituir la relación anterior producirá la siguiente ecuación.
[math]
\bar{y}= frac{2}{bh}\En t_{0}^{h} \frac{b}{h}y^{2}dos
[math]
Simplificando,
[math]
\bar{y}= frac{2}{h ^{2}}\izquierda [ \frac{y^{3}}{3} \verdad ]_ _{0}^{h}
[math]
[math]
\bar{y}= frac{2}{h ^{2}}\izquierda [ \frac{h ^{3}}{3}-0 \verdad ]
[math]
[math]
\bar{y}= frac{2}{3}h
[math]
Tenga en cuenta que esta solución se toma desde arriba. El centroide tomado del fondo debe ser igual a 1/3 de h.
Fórmula para centroides de formas y secciones de vigas comunes
A continuación se muestra una lista de un variedad de formas de sección de viga y la distancia a los centroides de la sección. Las ecuaciones muestran cómo encontrar el centroide de una sección particular desde la base o el punto más alejado de la sección. Para suscripciones de SkyCiv para estudiantes y estructurales, esta referencia también se puede descargar como una referencia en PDF para llevarla a donde quiera que vaya. Los centroides de una sección de la viga son extremadamente importantes ya que localizan el eje neutral y son uno de los primeros pasos requeridos al analizar una sección de la viga..
SkyCiv también ofrece una tabla completa de resumen de secciones que contiene todas las ecuaciones y fórmulas relacionadas con las secciones de la viga. (momento de inercia, área, etc.…).
La ecuación para varios centroides se enumeran a continuación:
| REFERENCIA | Cy (Distancia desde el fondo) |
Cx (Distancia desde el punto izquierdo más alejado) |
Centroide de rectángulo o secciones rectangulares |
||
|---|---|---|
 |
[math] \dfrac{h}{2} [math] |
[math] \dfrac{b}{2} [math] |
Centroide de una sección rectangular hueca |
||
 |
[math] \dfrac{b}{2} [math] |
[math] \dfrac{h}{2} [math] |
Centroide de un círculo o sección circular |
||
 |
[math] \dfrac{re}{2} [math] |
[math] \dfrac{re}{2} [math] |
Ecuación centroide de una sección circular hueca |
||
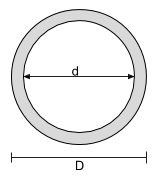 |
[math] \dfrac{re}{2} [math] |
[math] \dfrac{re}{2} [math] |
Centroide de un triángulo isósceles |
||
 |
[math] \dfrac{h}{3} [math] |
[math] \dfrac{b}{2} [math] |
Centroide de una viga I |
||
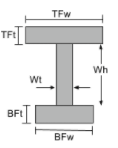 |
[math] \frac{TFw times TFt times left ( BFt + Wh + \frac{TFt}{2} \verdad )}{TFw times TFt + Wt times Wh + BFw times BFt} + [math] [math] \frac{Wt times Wh times left ( BFt + \frac{Wh}{2} \verdad )}{TFw times TFt + Wt times Wh + BFw times BFt} + [math] [math] \frac{BFw times BFt times left ( \frac{BFt}{2} \verdad )}{TFw times TFt + Wt times Wh + BFw times BFt} [math] |
[math] TFw > BFw, \frac{TFw}{2}[math] [math] BFw > TFw, \frac{BFw}{2} [math] |
Centroide de una sección en T |
||
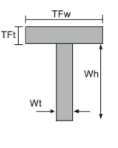 |
[math] \frac{Wt times Wh times left ( \frac{Wh}{2} \verdad )}{TFw times TFt + Wt times Wh } + [math] [math] \frac{TFw times TFt times left ( Wh + \frac{TFt}{2} \verdad ) }{TFw times TFt + Wt times Wh } [math] |
[math] \frac{TFw}{2} [math] |
Centroide de una cesárea |
||
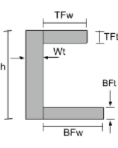 |
[math] \frac{TFw times TFt times left ( h – \frac{TFt}{2} \verdad )}{TFw times TFt + Wt times Wh + BFw times BFt} + [math] [math] \frac{Wt times h times left ( \frac{h}{2} \verdad )}{TFw times TFt + Wt times Wh + BFw times BFt} + [math] [math] \frac{BFw times BFt times left ( \frac{BFt}{2} \verdad )}{TFw times TFt + Wt times Wh + BFw times BFt} [math] |
[math] \frac{TFt times TFw times left ( Wt + \frac{TFw}{2} \verdad )}{TFt times TFw + h times Wt + BFt times BFw} + [math] [math] \frac{h times Wt times left ( \frac{Wt}{2} \verdad )}{TFt times TFw + h times Wt + BFt times BFw} + [math] [math] \frac{BFt times BFw times left ( Wt + \frac{BFw}{2} \verdad )}{TFt times TFw + h times Wt + BFt times BFw} [math] |
Centroide de ángulos |
||
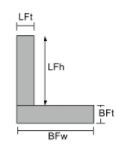 |
[math] \frac{LFt times LFh times left ( BFt + \frac{LFh}{2} \verdad ) }{LFt veces LFh + BFw times BFt} + [math] [math] \frac{BFw times BFt times left ( \frac{BFt}{2} \verdad )}{LFt veces LFh + BFw times BFt} [math] |
[math] \frac{LFh veces LFt veces izquierda ( \frac{LFt}{2} \verdad )}{LFh veces LFt + BFt times BFw} + [math] [math] \frac{BFt times BFw times left ( \frac{BFw}{2} \verdad )}{LFh veces LFt + BFt times BFw} [math] |
Ecuaciones automáticas para el centroide de la viga
Consulte nuestro Calculadora de centroides gratis, una versión simplificada de SkyCiv Section Builder, para calcular el centroide de la viga automáticamente sin necesidad de cálculos manuales. O regístrate hoy para empezar!


