Tabla de contenido

• Cálculo del diagrama de momento flector
• Cálculo manual del diagrama del momento flector
• Convención de signos para diagramas de momento de flexión
• Cómo calcular la flexión usando SkyCiv Beam

Cálculo del diagrama de momento flector

A continuación hay instrucciones simples sobre cómo calcular el diagrama de momento de flexión de una viga simplemente apoyada. Estudie este método ya que es muy versátil. (y se puede adaptar a muchos tipos diferentes de problemas. La capacidad de calcular el momento de una viga es una práctica muy común para los ingenieros estructurales y, a menudo, surge en los exámenes de la universidad y la escuela secundaria. Es bueno comentar, que el software SkyCiv Beam puede mostrar estos los cálculos manuales instantánea y automáticamente! Seguiremos el tutorial de hoy con un ejemplo tomado directamente del módulo de cálculo manual en SkyCiv Beam.

En primer lugar, ¿qué es un momento de flexiónt? Un momento es una fuerza de rotación que ocurre cuando una fuerza se aplica perpendicularmente a un punto a una distancia dada de ese punto. Se calcula como la fuerza perpendicular multiplicada por la distancia desde el punto. Un momento flector es simplemente el doblez que ocurre en una viga debido a un momento.

Es importante recordar dos cosas al calcular los momentos de flexión; (1) las unidades estándar son Nm y (2) cuando la fibra superior se comprime, la flexión se considera positiva. Con las definiciones fuera del camino, Veamos los pasos para calcular un diagrama de momento flector:

Calculadora gratis de vigas

Cálculo manual del diagrama del momento flector

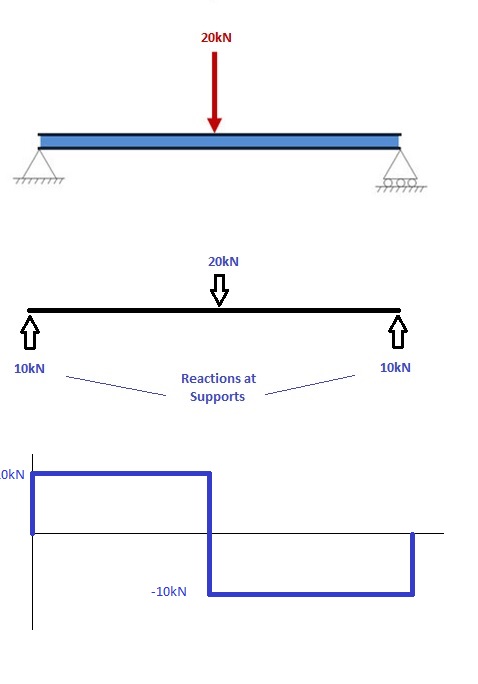
1. Calcular reacciones en soportes y dibujar Diagrama de cuerpo libre (FBD)

Si no estás seguro de cómo determinar las reacciones en los soportes – por favor mira este tutorial primero. Una vez que tengas las reacciones, dibuja tu diagrama de cuerpo libre y Diagrama de fuerza de cortante debajo de la viga. Finalmente, el cálculo de los momentos se puede hacer en los siguientes pasos:

2. De izquierda a derecha, hacer “cortes” antes y después de cada reacción / carga

Para calcular el momento flector de una viga, debemos trabajar de la misma manera que lo hicimos para el diagrama de fuerza de corte. Comenzando en x = 0 nos moveremos a través de la viga y calcularemos el momento flector en cada punto.

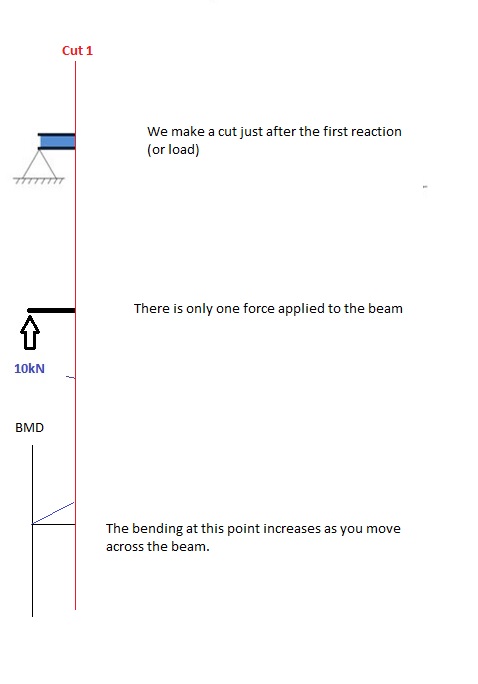
Corte 1

Hacer un “corte” justo después de la primera reacción de la viga. En nuestro sencillo ejemplo:

Entonces, cuando cortamos la viga, solo consideramos las fuerzas que se aplican a la izquierda de nuestro corte. En este caso, tenemos una fuerza de 10 kN en dirección ascendente. Ahora como lo recuerdas, un momento flector es simplemente la fuerza x distancia. Entonces a medida que nos alejamos de la fuerza, la magnitud del momento flector aumentará. Podemos ver esto en nuestra DMO. La ecuación para esta parte de nuestro diagrama de momento flector es:

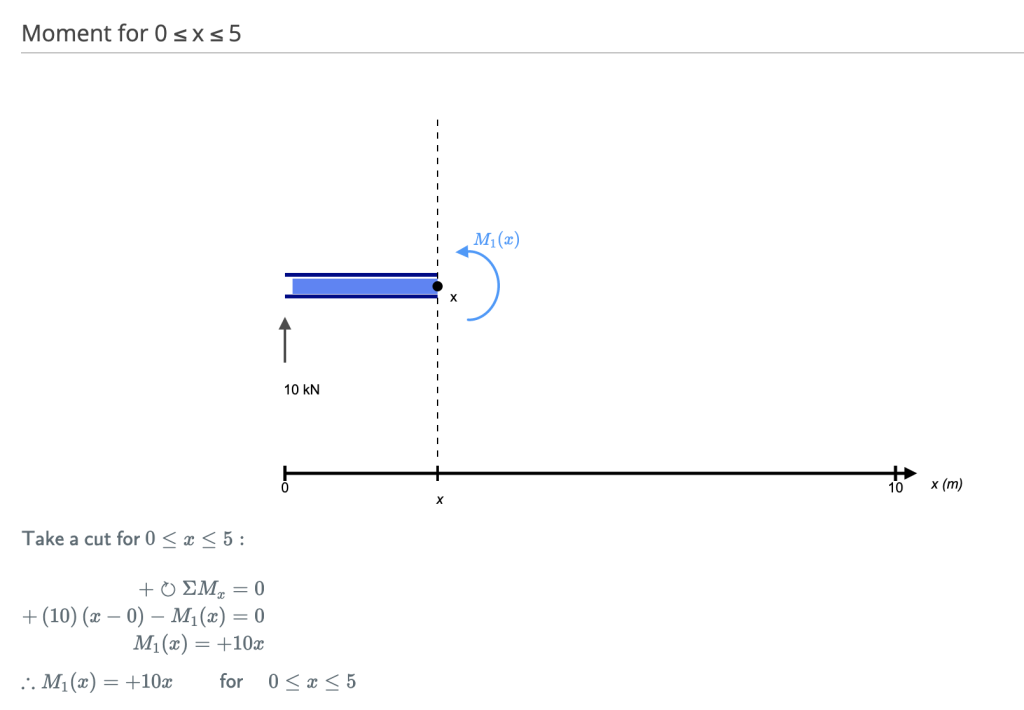
[Fuente: SkyCiv Módulo de cálculo manual de una viga]

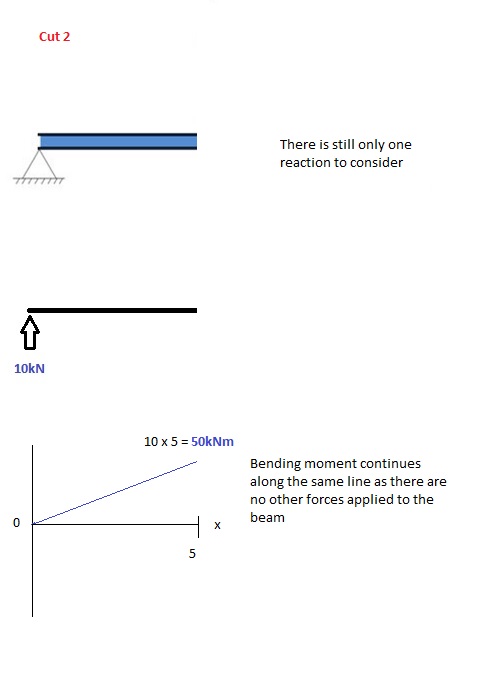
Corte 2

Este corte se realiza justo antes de la segunda fuerza a lo largo de la viga.. Como no hay otras cargas aplicadas entre el primer y el segundo corte, la ecuación del momento de flexión seguirá siendo la misma. Esto significa que podemos calcular el momento flector máximo (en este caso en el punto medio, o x = 5) simplemente sustituyendo x = 5 en la ecuación anterior:

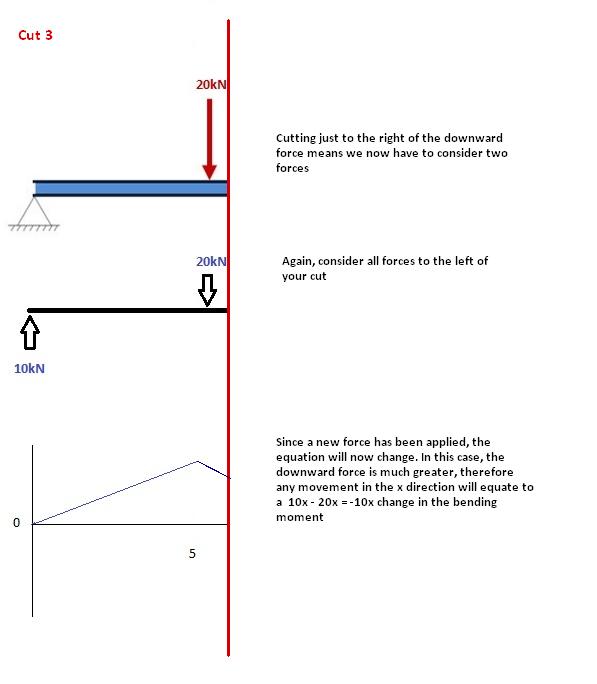
Corte 3

Este corte se realiza justo después de la segunda fuerza a lo largo de la viga.. Ahora tenemos DOS fuerzas que actúan a la izquierda de nuestro corte.: una reacción de soporte de 10kN y una carga de acción descendente de -20kN. Así que ahora debemos considerar ambas fuerzas a medida que avanzamos a lo largo de nuestra viga. Por cada metro que nos movemos a través de la viga, habrá un momento de + 10kNm agregado desde la primera fuerza y ​​-20kNm desde la segunda.

Entonces después del punto x = 5, nuestra ecuación de momento flector se convierte en: M(x) = 50 +10(x-5) – 20(x-5) M(x) = 50 -10(x-5) para 5 ≤ x ≤ 10 NOTA: La razón por la que escribimos (x-5) es porque queremos saber la distancia desde el pt x = 5 solamente. Cualquier cosa antes de este punto usa una ecuación previa.[Fuente: SkyCiv Módulo de cálculo manual de una viga]

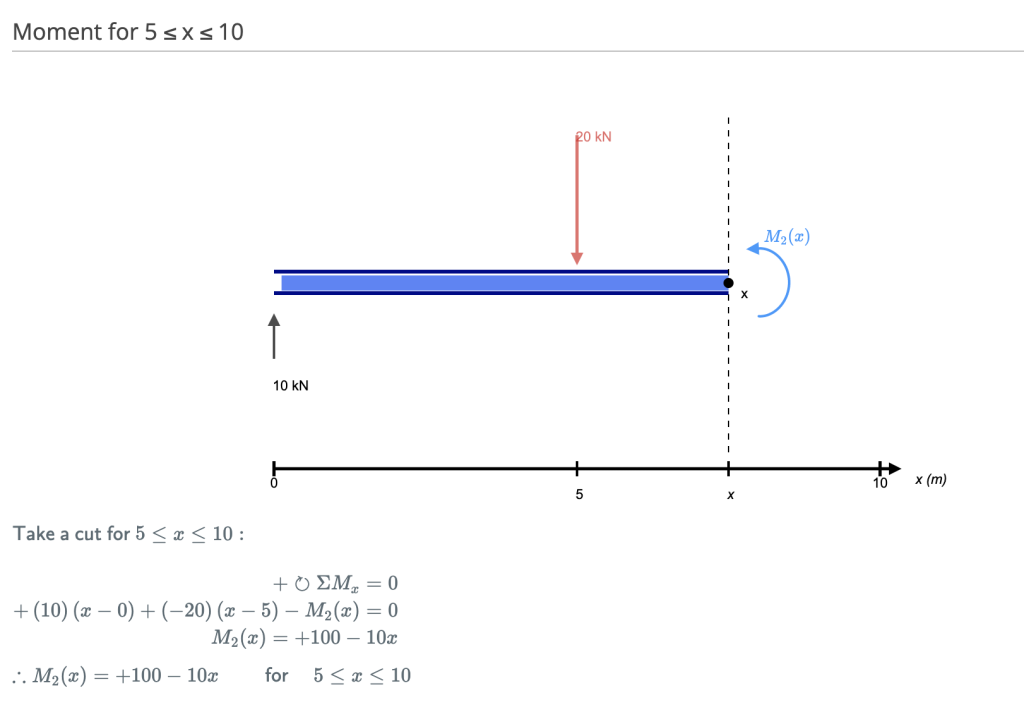
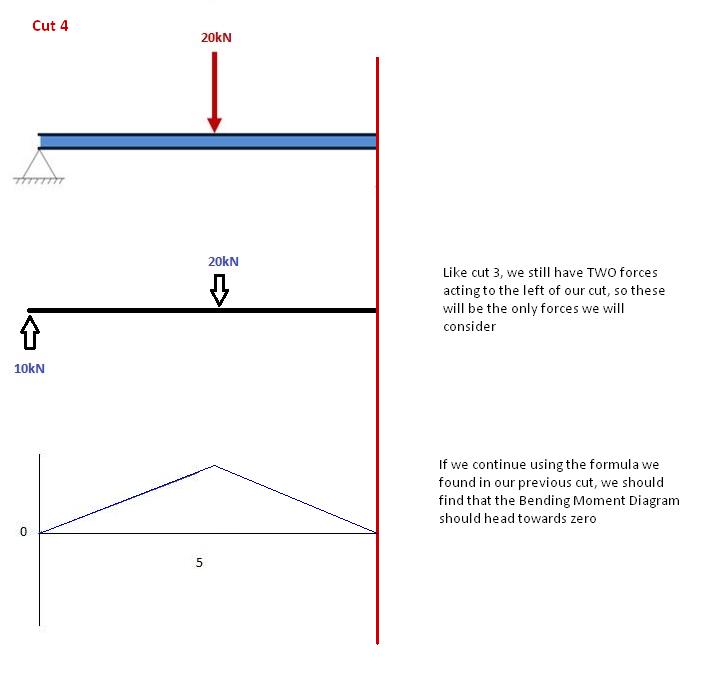
Corte 4

De nuevo, movámonos a la derecha de nuestra viga y hagamos un corte justo antes de nuestra próxima fuerza. En este caso, nuestro próximo corte ocurrirá justo antes de la reacción del soporte derecho. Como no hay otras fuerzas entre el soporte y nuestro corte anterior, la ecuación seguirá siendo la misma: M(x) = 50 -10(x-5) para 5 ≤ x≤ 10 Y sustituyamos x = 10 en esto para encontrar el momento de flexión de búsqueda al final de la viga: M(x) = 50 – 10(10-5) = 0kNm Esto tiene mucho sentido. Como nuestra viga es estática (y sin rotación) tiene sentido que nuestra viga deba tener cero momentos en este punto cuando consideramos todas nuestras fuerzas. También satisface una de nuestras condiciones iniciales., que la suma de momentos en el apoyo es igual a cero. NOTA: Si sus cálculos lo llevan a cualquier otro número que no sea 0, ha cometido un error!

El resultado final, como se muestra en SkyCiv Beam:

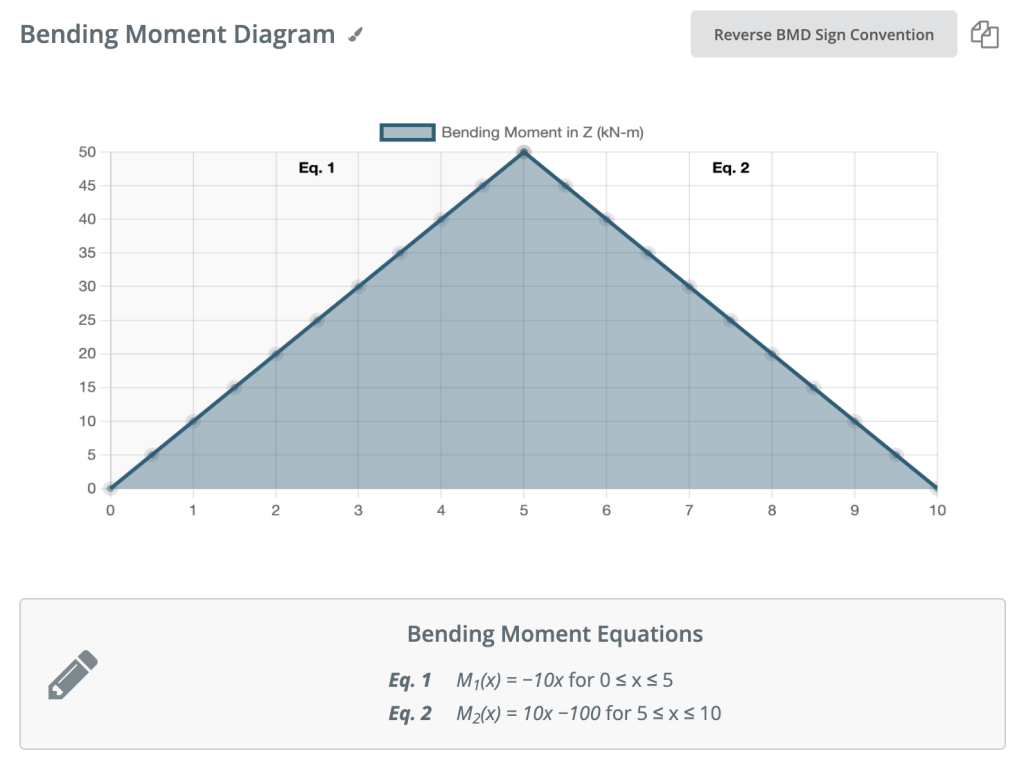
Convención de signos para diagramas de momento de flexión

Los diagramas de momentos de flexión pueden ser algo confusos cuando se trata de convenciones de signos. Es posible que vea el mismo diagrama dibujado en direcciones opuestas dependiendo de la fuente. La convención de signos utilizada por SkyCiv se muestra a continuación..

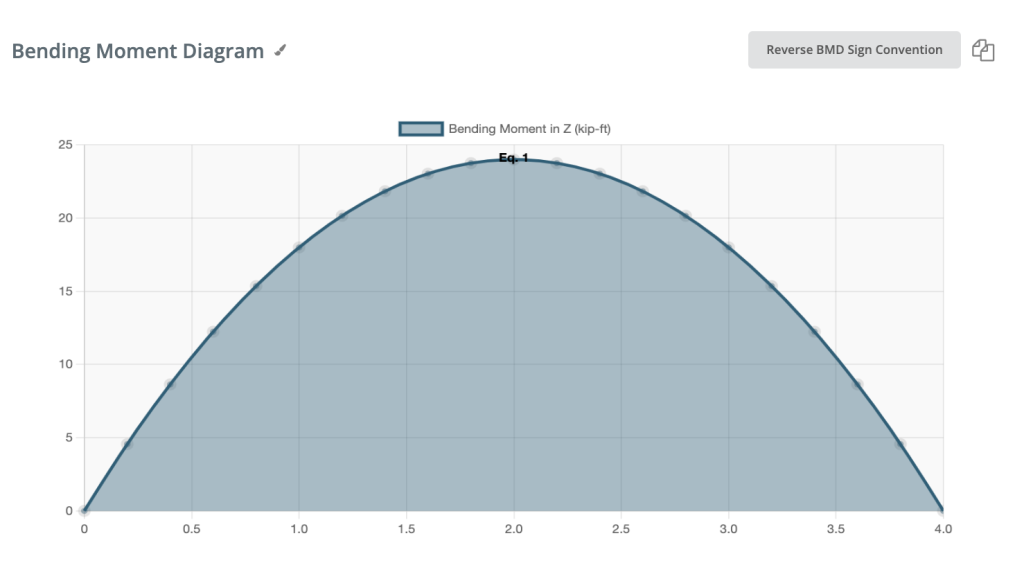
Momento de flexión positivo:

Si el momento flector es positivo, la fibra superior de la viga está comprimida.

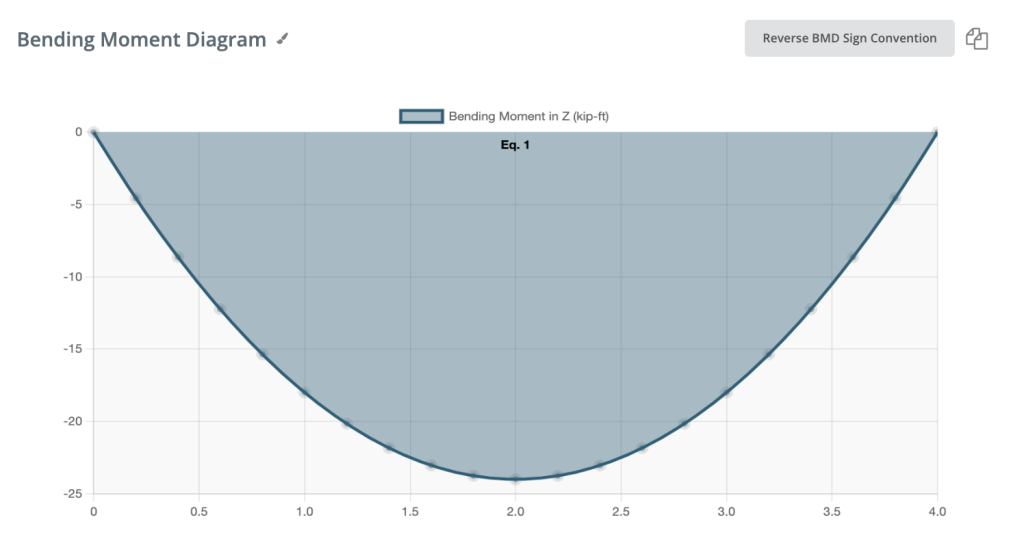
Momento de flexión negativo:

Si el momento flector es negativo, la fibra inferior de la viga está comprimida.

BONO: ¿Cómo calcular la flexión con SkyCiv Beam?

Bajo nuestra versión paga de SkyCiv Beam la calculadora incluso te mostrará los cálculos manuales completos, mostrando los pasos dados para calcular a mano los diagramas de momento flector. Simplemente modele su viga usando la calculadora, y pulse resolver. Le mostrará los cálculos paso a paso de cómo dibujar un diagrama de momento de flexión (incluyendo cortes):