Un ejemplo completamente trabajado de NBCC 2015 cálculos de carga de nieve
La acumulación de nieve en las estructuras puede ser muy peligrosa para los miembros del techo u otros elementos estructurales expuestos.. El Código Nacional de Construcción de Canadá (2015) División B – Sección de 4.1.6 proporciona un cálculo detallado de las cargas de nieve y las cargas de lluvia asociadas. Usando esta guía, demostraremos cómo calcular las cargas de nieve usando un ejemplo de Structural 3D (S3D) modelo de almacén, Como se muestra abajo:
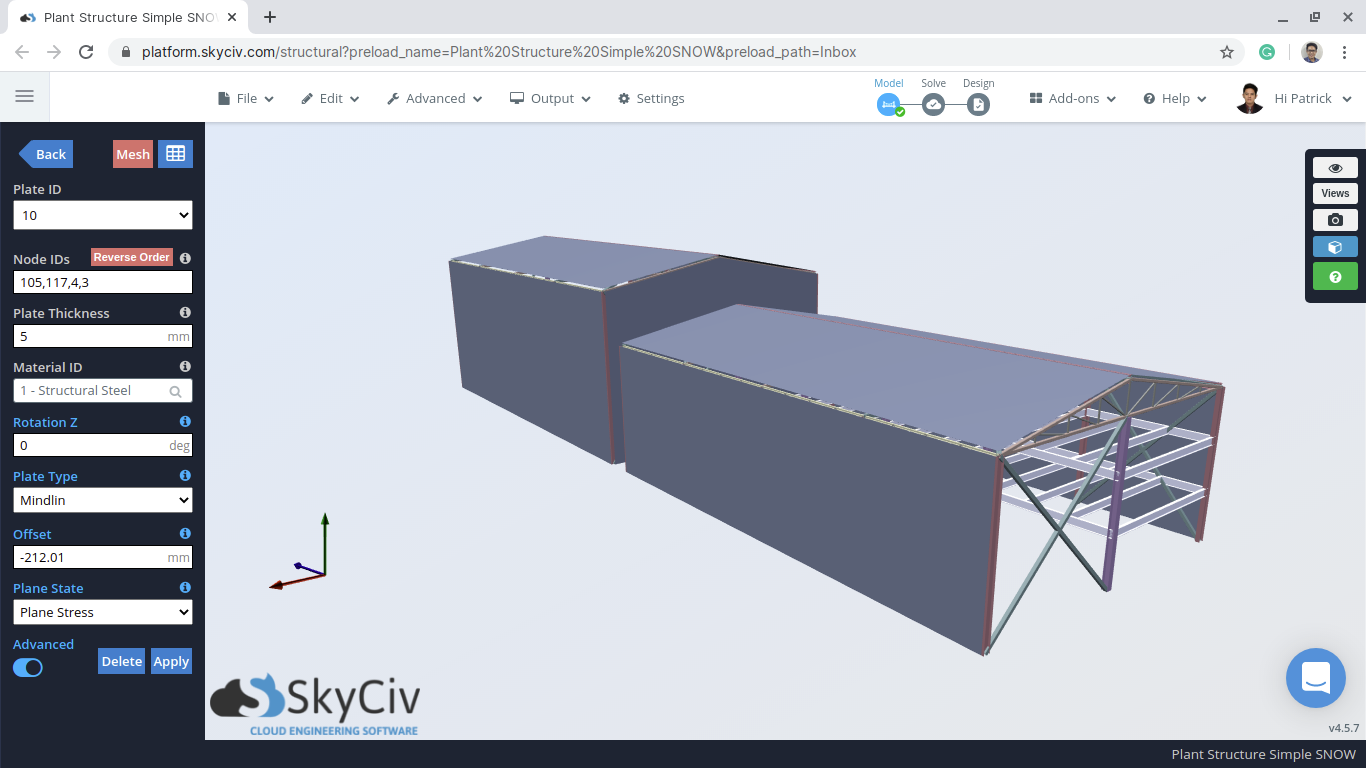
Figura 1: Ejemplo de modelo de almacén S3D

Figura 2: Ubicación del sitio de ejemplo usando Google Maps (solo para ilustracion).
Tabla 1: Datos de construcción necesarios para nuestro cálculo de carga de nieve.
| Ubicación | Ogden, Calgary, Alberta (solo para ilustracion) |
| Ocupación | Almacén o almacenamiento de materiales |
| Dimensiones | 19.508 m x 31.70 m para cada estructura Altura del alero de un edificio más pequeño 9.144 m Altura del ápice de un edificio más pequeño 11.941 m La diferencia de techo superior e inferior es 3.50 m Ángulo de inclinación del techo 16° |
| Detalles adicionales | El techo tiene una superficie resbaladiza El espacio entre estructuras es 2.30 m |
De la tabla 1, la carga de nieve especificada, \(S), se puede calcular usando la fórmula:
\(S = {I}_ _{s}[{S}_ _{s}{C}_ _{b}{C}_ _{w}{C}_ _{s}{C}_ _{a} +{S}_ _{r}]\) (1)
Dónde:
\({I}_ _{s}\) = factor de importancia para la carga de nieve, Tabla 4.1.6.2-A
\({S}_ _{s}\) = 1-carga de nieve en el suelo en 50 años, kPa, Subsección 1.1.3
\({C}_ _{b}\) = factor de carga de nieve del techo básico, 4.1.6.2 (2)
\({C}_ _{w}\) = basado en el factor de exposición al viento, 4.1.6.2 (3) y (4)
\({C}_ _{s}\) = factor de pendiente, 4.1.6.2 (5), (6), y (7)
\({C}_ _{a}\) = factor de acumulación, 4.1.6.2 (8)
\({S}_ _{r}\) = Carga de lluvia asociada a 1 de cada 50 años, kPa, Subsección 1.1.3, pero no mayor que \({S}_ _{s}{C}_ _{b}{C}_ _{w}{C}_ _{s}{C}_ _{a}\)
Cada parámetro se examinará individualmente en las siguientes secciones. Se calcularán los siguientes casos de carga de nieve: carga de nieve equilibrada y desequilibrada en cada techo (viento normal a la cresta), así como la deriva generada en el techo inferior considerando la acumulación por deslizamiento.
Factor de importancia, \({I}_ _{s}\)
Lo primero que se determina es el factor de importancia, \({I}_ _{s}\), que se encuentra usando Tabla 4.1.6.2-A como se hace referencia. Dado que la estructura es un edificio de almacenamiento que tiene un bajo impacto directo en la vida humana en caso de falla., la categoría de importancia es Bajo. Además, el cálculo estará en el estado límite último (ULS). Entonces de Tabla 4.1.6.2-A, \({I}_ _{s}\) es igual a 0.80.
| Categoría de importancia | Factor de importancia, \({I}_ _{s}\) | |
|---|---|---|
| ULS | SLS | |
| Bajo | 0.8 | 0.9 |
| Normal | 1.0 | 0.9 |
| Alto | 1.15 | 0.9 |
| Después del desastre | 1.25 | 0.9 |
Carga de nieve en el suelo, \({S}_ _{s}\), y carga de lluvia asociada, \(({S}_ _{r})\)
La carga de nieve del suelo, \({S}_ _{s}\), y carga de lluvia asociada, \(({S}_ _{r})\), los valores están tabulados en Apéndice C, División B de NBCC 2015 dependiendo de la ubicación y la provincia. En este ejemplo, el correspondiente \({S}_ _{s}\) y \(({S}_ _{r})\) in Calgary, Alberta es igual a 1.10 kPa y 0.1 kPa, respectivamente.
Tener dificultades para buscar la nieve del suelo y la carga de lluvia asociada para NBCC 2015? Prueba la Herramienta generadora de carga libre SkyCiv para acelerar su búsqueda y obtener el correspondiente \({S}_ _{s}\) y \({S}_ _{r}\) basado en la ubicación de su estructura.
Factor de exposición al viento, \({C}_ _{w}\)
Para el factor de exposición al viento, \({C}_ _{w}\), se permitirá que sea igual a 1.0 Residencia en 4.1.6.2 (3). Este factor aún puede reducirse siempre que las condiciones en 4.1.6.2 (4) Está satisfecho. En este ejemplo, \({C}_ _{w}\) será igual a 1.0 ya que la ubicación no es un terreno abierto que exponga completamente la estructura al viento.
Factor básico de carga de nieve en el techo, \({C}_ _{b}\)
El factor de carga de nieve básico del techo, \({C}_ _{b}\), se puede calcular usando las siguientes fórmulas, como se menciona en 4.1.6.2 (2):
\({C}_ _{b} = 0.8\) (2) para \({l}_ _{c} ≤ (70/{{C}_ _{w}}^{2})\) y
\({C}_ _{b} = (1/{C}_ _{w}) [1 – (1 – 0.8{C}_ _{w})Exp(-0.01({l}_ _{c}{{C}_ _{w}}^{2} – 70))] \) (3) para \({l}_ _{c} > (70/{{C}_ _{w}}^{2})\)
Dónde:
\({l}_ _{c}\) = longitud característica del techo superior o inferior definido como: \(2w -{w}^{2}/l )
\(l ) = dimensión en planta más grande del techo
\(w\) = dimensión en planta más pequeña del techo
En este ejemplo,\(l ) y \(w\) es igual a 31.7 my 19.51 m, respectivamente, por lo tanto, \({l}_ _{c}\) es igual a 27.01. Ya que \({l}_ _{c}\) es menos que \((70/{1.0}^{2})\), el factor básico de carga de nieve del techo, \({C}_ _{b}\), es igual a 0.8.
Factor de pendiente, \({C}_ _{s}\)
El cálculo del factor de pendiente es \({C}_ _{s}\) detallado en 4.1.6.2 (5), (6), y (7) se muestra a continuación.
Para techo resbaladizo sin obstrucciones:
\({C}_ _{s} = 1.0\) para \(α ≤ 15°\)
\({C}_ _{s} = 0\) para \(una > 60° )
\({C}_ _{s} = (60° – una)/45° ) para \(15° < α ≤ 60°\)
Para otros casos:
\({C}_ _{s} = 1.0\) para \(α ≤ 30°\)
\({C}_ _{s} = 0\) para \(una > 70° )
\({C}_ _{s} = (70° – una)/40° ) para \(30° < α ≤ 70°\)
Peso específico de la nieve, \(γ\)
El peso específico de la nieve se especifica en 4.1.6.13 y se tomará como:
\(γ = 0.43{S}_ _{s} + 2.2 kN /{m}^{3} ≤ 4.0 kN /{m}^{3}\) (4)
En este ejemplo, \(γ\) es igual a \(2.673 kN /{m}^{3}\).
Factor de acumulación, \({C}_ _{a}\)
Factor de acumulacion, \({C}_ _{a}\), w w 4.1.6.2 (8). w.
Carga de nieve especificada, \(S)
En esta sección, la carga de nieve especificada, \(S), se calculará para los casos equilibrado y derivado.
Estuche equilibrado / sin aros
Para el caso equilibrado / sin derrames, la factor de acumulación \({C}_ _{a}\) es igual a 1.0. Además, w \(α\) es \(16° ) y se asume que la superficie del techo está resbaladiza sin obstrucciones, el factor de pendiente, \({C}_ _{s}\), para nuestro ejemplo es igual a 0.978. Usando la ecuación (1), la carga de nieve especificada, \(S), para caso equilibrado / sin derrames es:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa
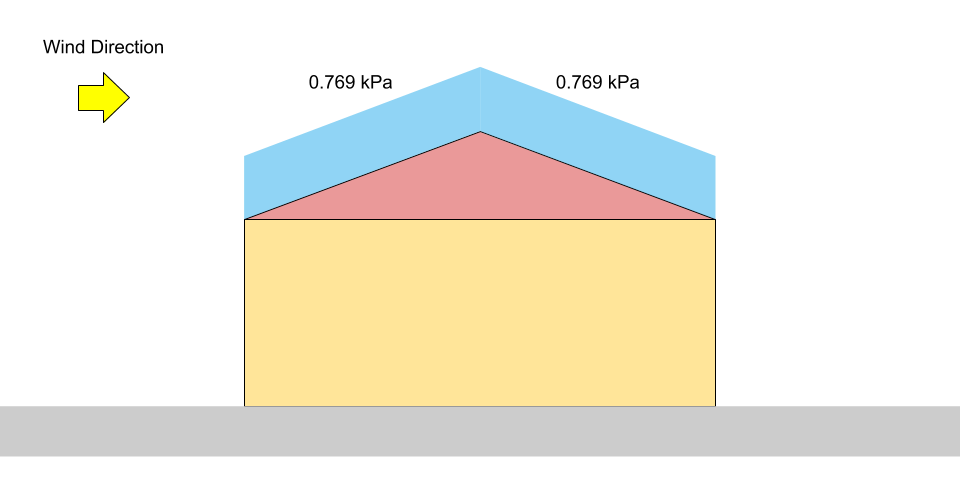
Figura 3: Diagrama de carga para carga de nieve equilibrada en un techo a dos aguas.
Estuche desequilibrado / desviado
El viento actúa de forma normal a la cresta
Dado que las estructuras tienen techos a dos aguas, la carga de nieve desequilibrada (viento actuando normal a la cresta) factor de acumulación \({C}_ _{a}\) se encuentra usando 4.1.6.9:
\({C}_ _{a, contra el viento} = 0\)
\({C}_ _{a, viento abajo} = 0.25 +α/20\) para \(15° ≤ α ≤ 20°\)
\({C}_ _{a, viento abajo} = 1.25\) para \(20° < α ≤ 90°\)
Debido a que ambas estructuras tienen un ángulo de inclinación del techo igual a 16 °, los factores de acumulación \({C}_ _{a, contra el viento}\) y \({C}_ _{a, viento abajo}\) son iguales a 0 y 1.05, respectivamente. Además, w \(α\) es \(16° ) y se asume que la superficie del techo está resbaladiza sin obstrucciones, el factor de pendiente, \({C}_ _{s}\), para nuestro ejemplo es igual a 0.978.
En el caso desbalanceado / desviado normal a la cresta, \({C}_ _{a}\) se calculará sobre la base de 4.1.6.9 para una caja de techo a dos aguas. Del cálculo anterior, \({C}_ _{a, contra el viento} = 0\) y \({C}_ _{a, viento abajo} = 1.05\). Por lo tanto, las cargas de nieve especificadas para cada lado son:
\({S}_ _{contra el viento} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({pag}_ _{1}\)
\({S}_ _{viento abajo} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({pag}_ _{2}\)
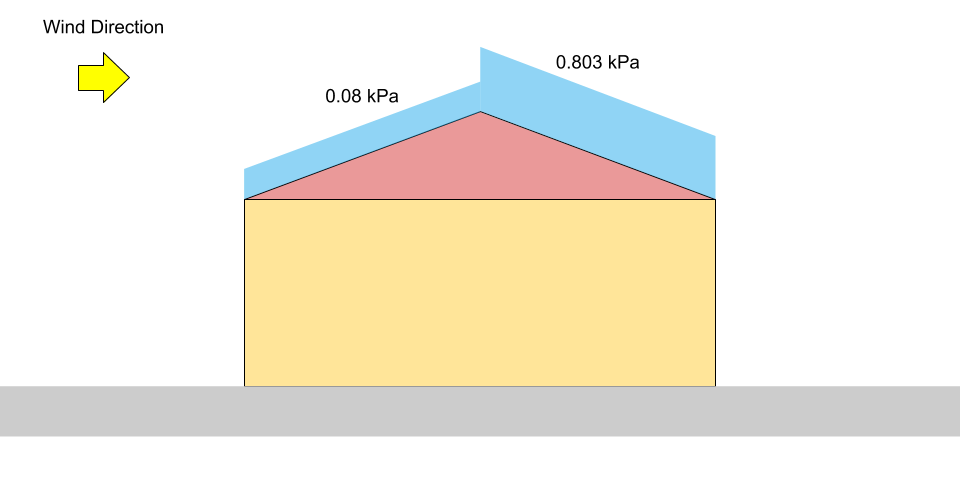
Figura 4: Diagrama de carga para carga de nieve desequilibrada en un techo a dos aguas (no escalar).
El viento actúa en paralelo a la cresta – Caso I – Viento desde el techo superior al inferior
Cuando el viento actúa paralelo a la cresta, lo más probable es que se desarrolle un ventisquero en el techo inferior. w factor de acumulación \({C}_ _{a}\), las siguientes fórmulas de 4.1.6.2 (8) son usados:
\({C}_ _{a} ={C}_ _{a0} – ({C}_ _{a0} – 1)(X/{x}_ _{d})\) para \(0 ≤ x ≤ {x}_ _{d}\)
\({C}_ _{a} = 1.0\) para \(x > {x}_ _{d}\)
Dónde:
\({C}_ _{a0}\) = valor pico de \({C}_ _{a0}\) en x = 0
\(X) = distancia desde el escalón del techo
\({x}_ _{d}\) = longitud de la deriva como se muestra en la Figura 3 a continuación

Figura 5: Ilustración de los parámetros de las dimensiones del techo

Figura 6: Carga de deriva correspondiente en el techo inferior basado en Figura 4.1.6.5-A.
\({C}_ _{a0}\) y \({x}_ _{d}\) se puede calcular usando las siguientes fórmulas:
\({C}_ _{a0} = frac{βγh}{{C}_ _{b}{S}_ _{s}}\) o \({C}_ _{a0} = frac{F}{{C}_ _{b}}\) (5), lo que sea menor
\({x}_ _{d} = 5 \frac{{C}_ _{b}{S}_ _{s}}{C}({C}_ _{a0} – 1)\) (6)
\(F = 0.35β\sqrt{\frac{C({l}_ _{cs} – 5{{h}_ _{pag}}^{"})}{{S}_ _{s}}} +{C}_ _{b}\) pero \(F ≤ 5\) para \({C}_ _{ws} = 1.0\) (7)
\({h}^{"} = h – \frac{{C}_ _{b}{C}_ _{w}{S}_ _{s}}{C}\) (8)
\({{h}_ _{pag}}^{"} ={h}_ _{pag} – \frac{0.8{S}_ _{s}}{C}\) pero \(0 ≤ {{h}_ _{pag}}^{"} ≤ \frac{{l}_ _{cs}}{5}\) (9)
Dónde:
\({h}_ _{pag}\) = altura del parapeto en el techo superior (0 en este caso ya que no hay parapeto)
\(h ) = diferencia de altura entre el nivel del techo superior e inferior
\({C}_ _{ws}\) = valor de \({C}_ _{w}\) aplicable a la fuente de la deriva
\({l}_ _{cs}\) = longitud característica del área fuente definida como: \(2{w}_ _{s} -{{w}_ _{s}}^{2}/{l}_ _{s}\)
\({l}_ _{s}\) = dimensión en planta más grande del área de origen como se muestra en la Figura 7 y 8, mostrada a continuación
\({w}_ _{s}\) = dimensión en planta más pequeña del área de origen como se muestra en la Figura 7 y 8, mostrada a continuación
\(β ) = 1.0 para el caso I, y 0.67 para los casos II y III.
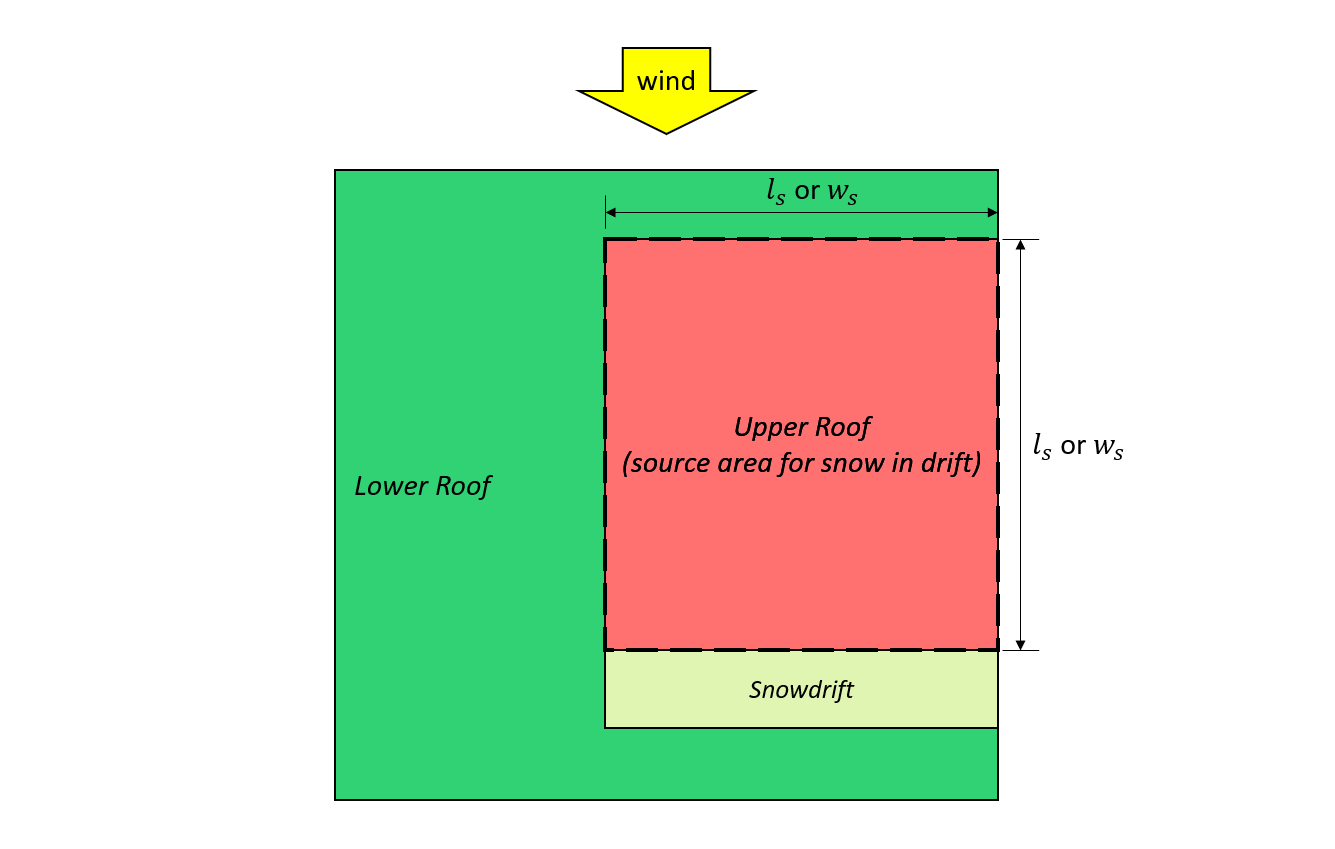
Figura 7: Caso I – ventisquero formado por el viento proveniente del techo superior basado en Figura 4.1.6.5-B.
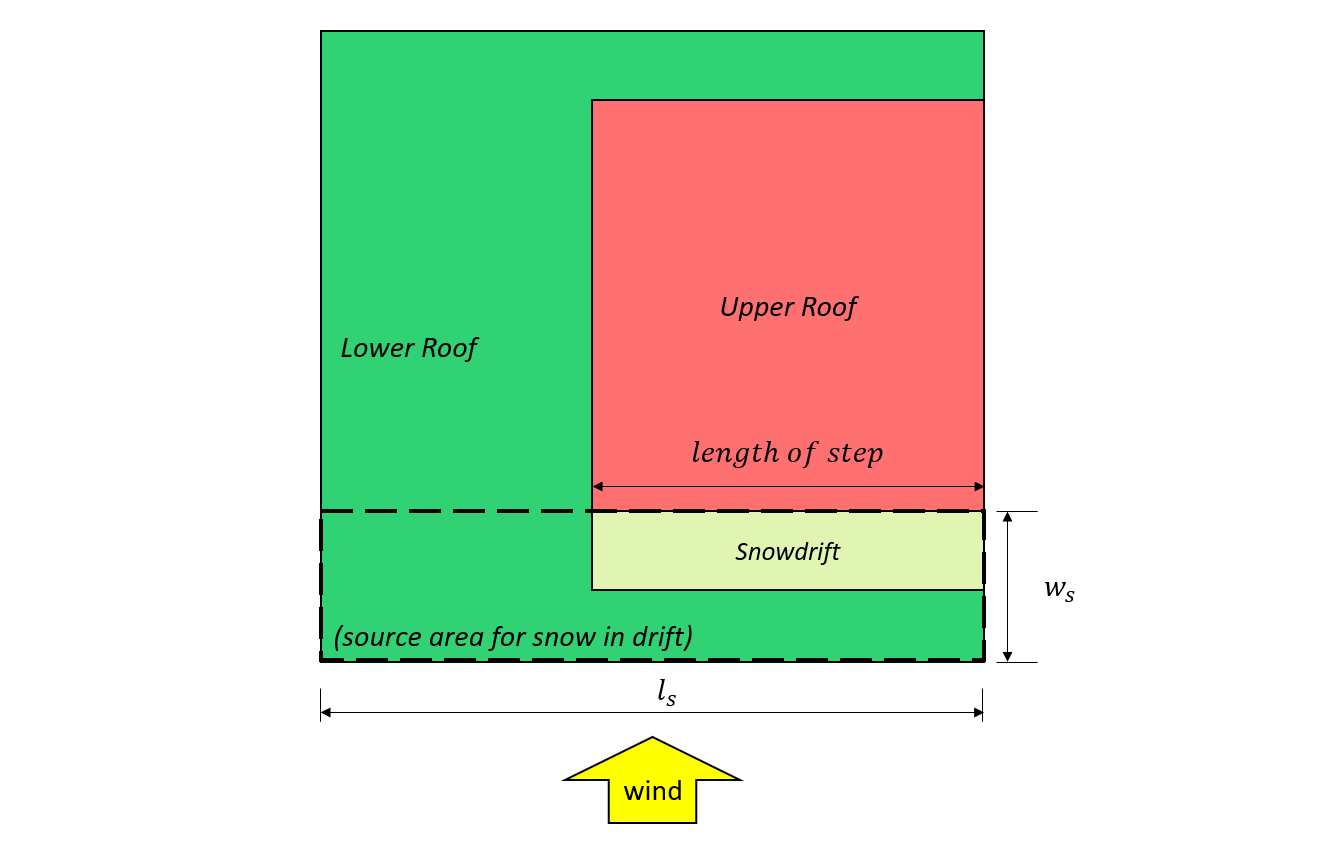
Figura 8: Caso II – ventisquero formado por el viento procedente del techo inferior basado en Figura 4.1.6.5-B.
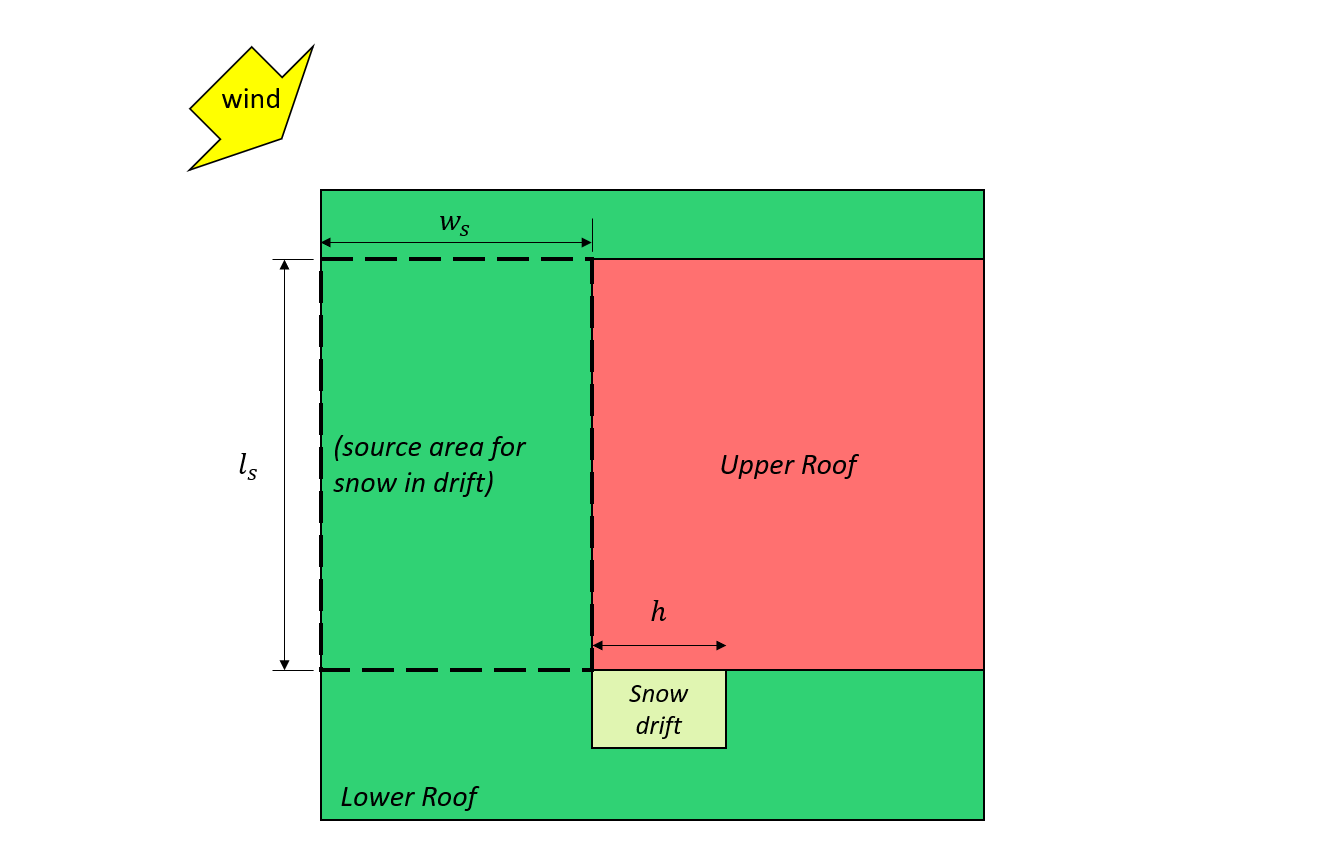
Figura 7: Caso III – ventisquero parcial formado por el viento procedente del techo inferior basado en Figura 4.1.6.5-B.
En este ejemplo, Se considerarán los casos I y II.
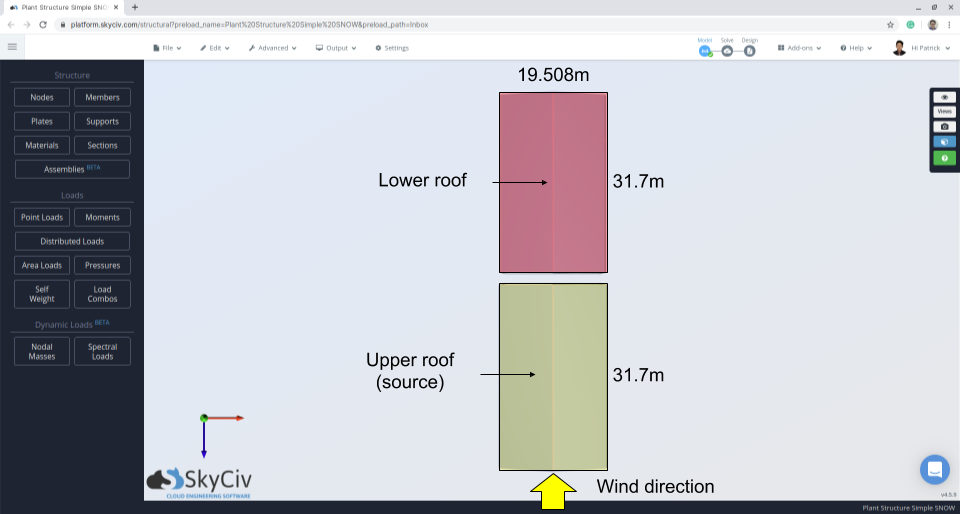
Figura 10: Plano de la estructura que indica la dirección del viento y el área de la fuente.
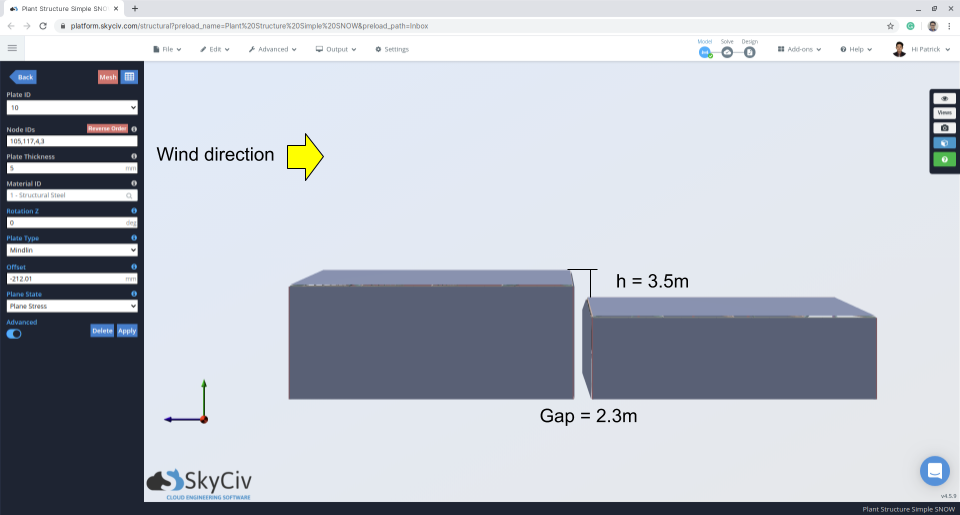
Figura 11: Vista de elevación que indica el espacio y la diferencia del techo superior e inferior.
Para el caso desbalanceado / derivado paralelo a la cresta, \({C}_ _{a}\) se calculará para el Caso I y el Caso II sobre la base de 4.1.6.5 para el techo de varios niveles. Para el caso I, Estos siguientes parámetros deben calcularse primero utilizando las diversas ecuaciones mencionadas anteriormente en este ejemplo.:
\(β = 1.0\)
\({h}^{"} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 metro)
\({h}_ _{pag} = 0\)
\({{h}_ _{pag}}^{"} =0\)
\({l}_ _{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 metro)
\(F = 0.35(1.0)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({C}_ _{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) o \({C}_ _{a0} = frac{3.66}{0.8} = 4.544\)
\({C}_ _{a0} = 4.544\)
\({x}_ _{d} = 5 \frac{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 metro)
De estos parámetros, el factor de acumulación, \({C}_ _{a}\), se puede calcular sustituyendo el valor de \({C}_ _{a0}\) en cada \(X) distancia. Tenga en cuenta que tenemos que calcular \({C}_ _{a}\) a \(x = a\) dónde \(una) es el espacio entre el techo, ya que el espacio del techo es menor que 5 m como se especifica en 4.1.6.6.
a \(x = 0\): \({C}_ _{a} = 4.544 – (4.544 – 1)(0/5.835) = 4.544\)
a \(x = a\): \({C}_ _{a} = 4.544 – (4.544 – 1)(2.3/5.835) = 3.147\)
a \(x = {x}_ _{d}\): \({C}_ _{a} =1.0\)
a \(x = 10{h}^{"}\): \({C}_ _{a} =1.0\)
w w w, \({C}_ _{s} = 1.0\). Además, al encontrar la carga de nieve especificada en el techo superior, el factor de acumulación, \({C}_ _{a}\), y factor de pendiente, \({C}_ _{s}\), son ambos iguales a 1.0. Por lo tanto, la magnitud de las cargas de nieve especificadas en cada ubicación son:
a \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa)
a \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {pag}_ _{1}\)
a \(x = {x}_ _{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={pag}_ _{2} = {pag}_ _{3}\)
en el nivel superior del techo: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa)
El viento actúa en paralelo a la cresta – Caso II – Viento desde el techo inferior al superior
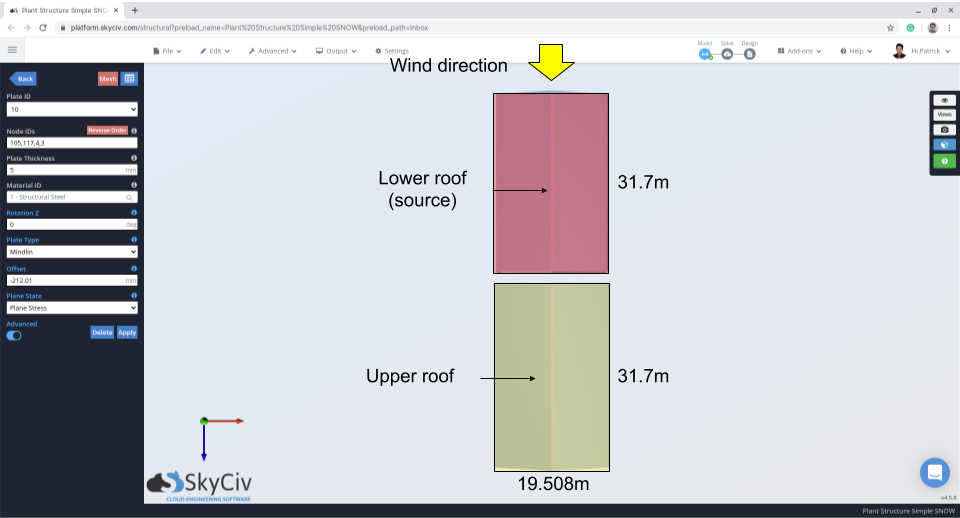
Figura 12: Plano de la estructura que indica la dirección del viento y el área de la fuente – viento desde el techo inferior al superior.
Para el caso II, el cálculo es similar al caso I, pero tiene una diferencia \(β = 0.67\):
\(β = 0.67\)
\({h}^{"} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 metro)
\({h}_ _{pag} = 0\)
\({{h}_ _{pag}}^{"} =0\)
\({l}_ _{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 metro)
\(F = 0.35(0.67)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({C}_ _{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) o \({C}_ _{a0} = frac{2.70}{0.8} = 3.375\)
\({C}_ _{a0} = 3.375\)
\({x}_ _{d} = 5 \frac{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 metro)
a \(x = 0\): \({C}_ _{a} = 3.375 – (3.375 – 1)(0/3.909) = 3.375\)
a \(x = a\): \({C}_ _{a} = 3.375 – (3.375 – 1)(2.3/3.909) = 1.978\)
a \(x = {x}_ _{d}\): \({C}_ _{a} =1.0\)
a \(x = 10{h}^{"}\): \({C}_ _{a} =1.0\)
a \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa)
a \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {pag}_ _{1}\)
a \(x = {x}_ _{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {pag}_ _{2} = {pag}_ _{3}\)
en el nivel superior del techo: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa)
Por ilustracion, el correspondiente \({pag}_ _{1}\), \({pag}_ _{2}\), y \({pag}_ _{3}\) se muestran en figuras 13 y 14 a continuación para los casos I y II, respectivamente.
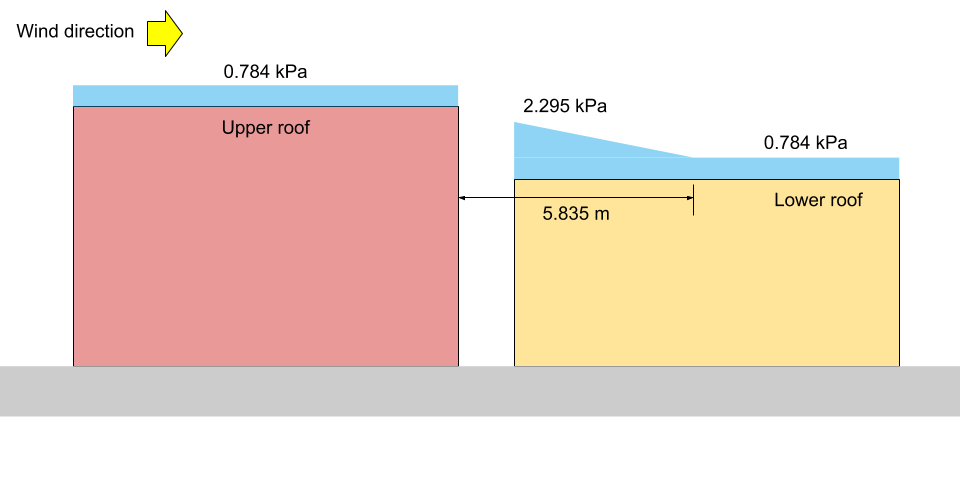
Figura 13: Ilustración de carga de nieve para el caso I (no escalar).
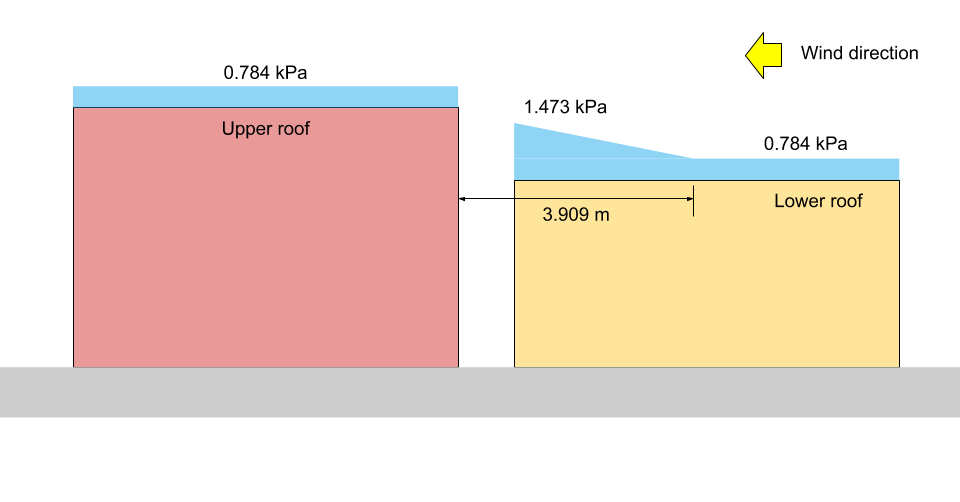
Figura 14: Ilustración de carga de nieve para Case II (no escalar).
Complete estos cálculos automáticamente en minutos
Eso fue un calculo largo, ¿Qué puede hacer como ingeniero para acelerar este proceso para sus proyectos futuros?? Recientemente, SkyCiv ha lanzado un generador de carga de nieve automatizado como parte del generador de carga SkyCiv., que también puede generar cargas de viento. Para encontrar las cargas de nieve del ejemplo mostrado, solo se necesitan unos pocos clics con la herramienta:
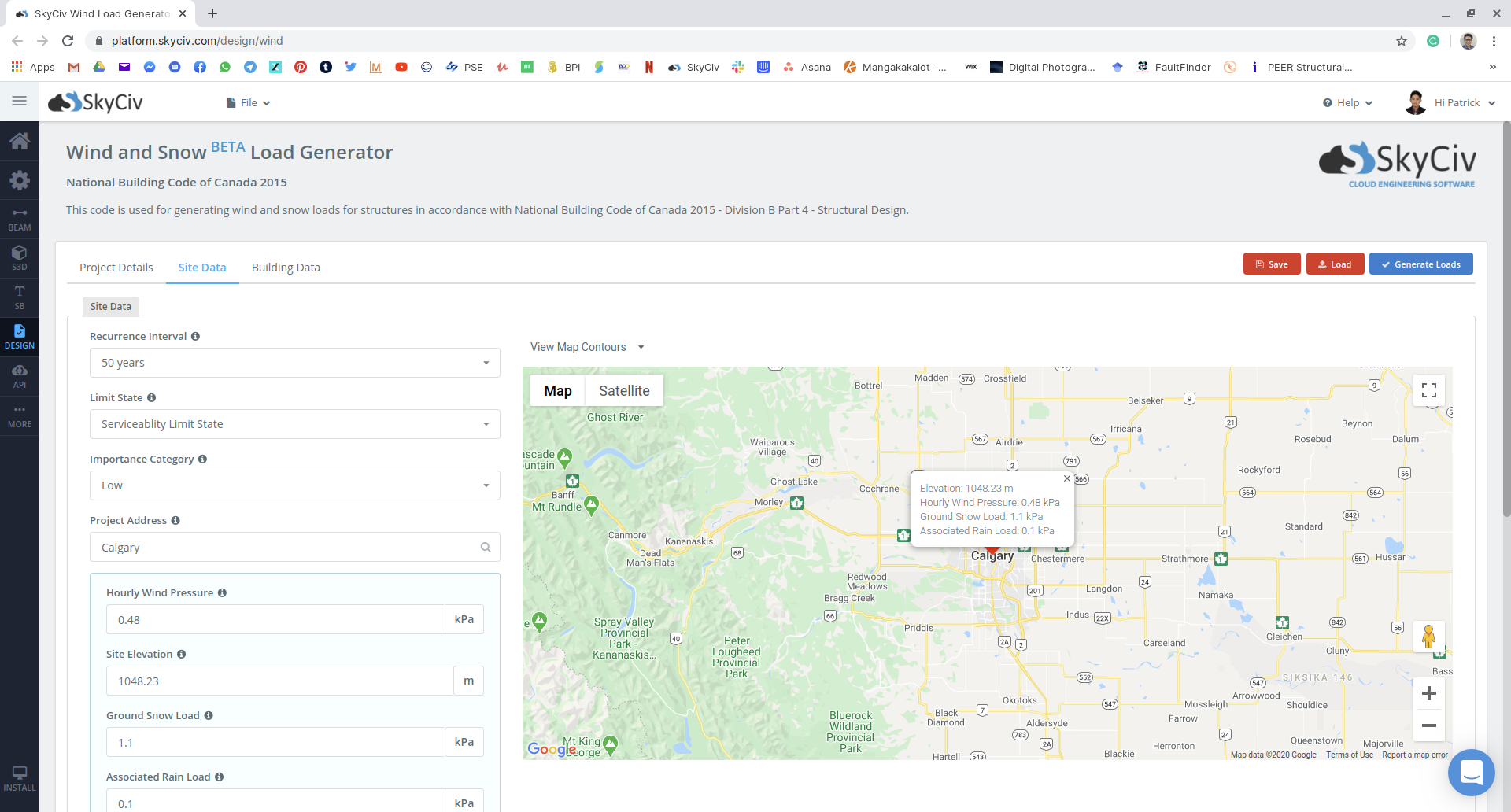
Figura 15: Entrada de datos del sitio en el módulo SkyCiv Load Generator usando nuestro ejemplo.
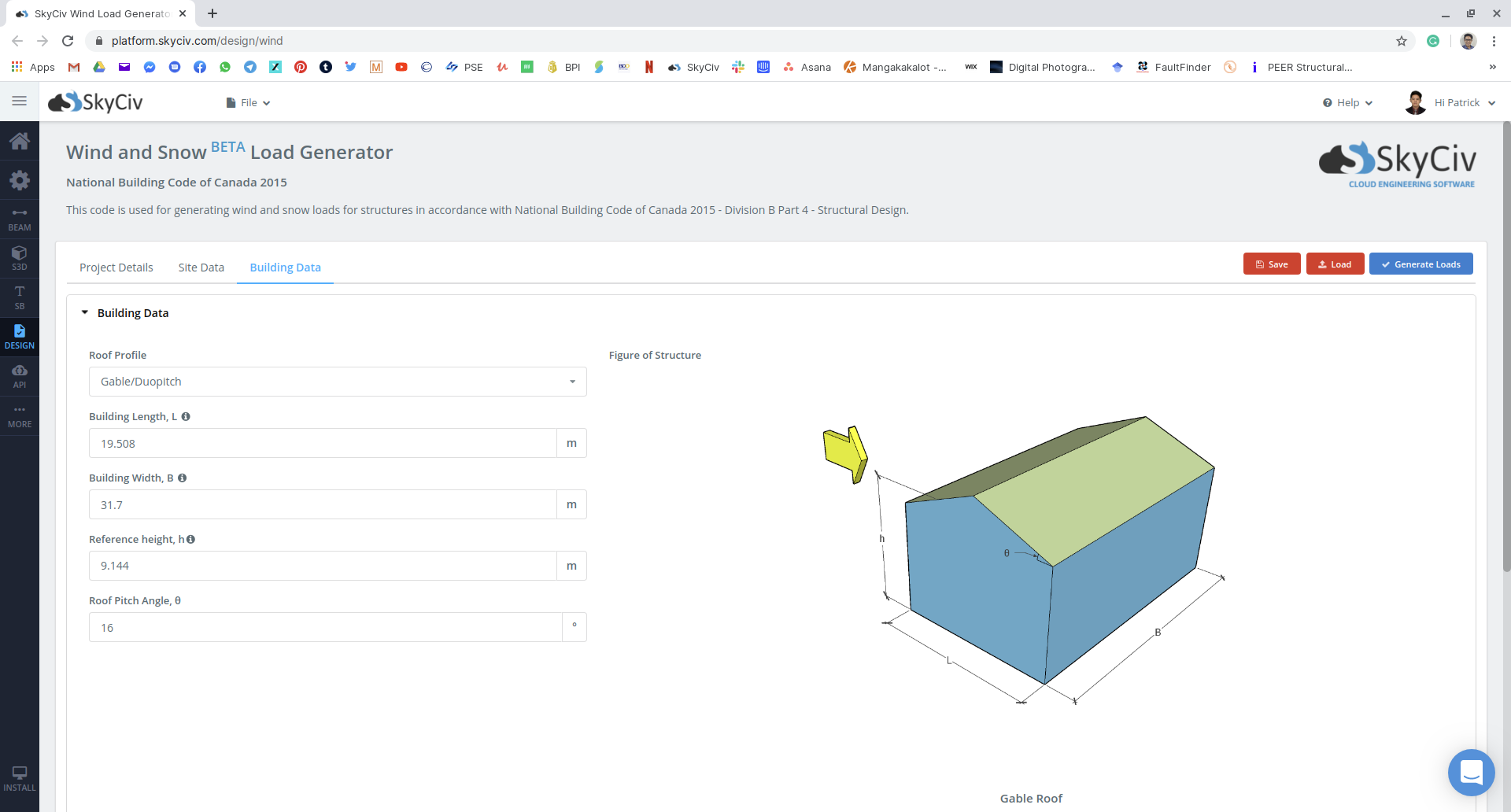
Figura 16: Entrada de parámetros de construcción y nieve en el módulo generador de carga SkyCiv usando nuestro ejemplo.
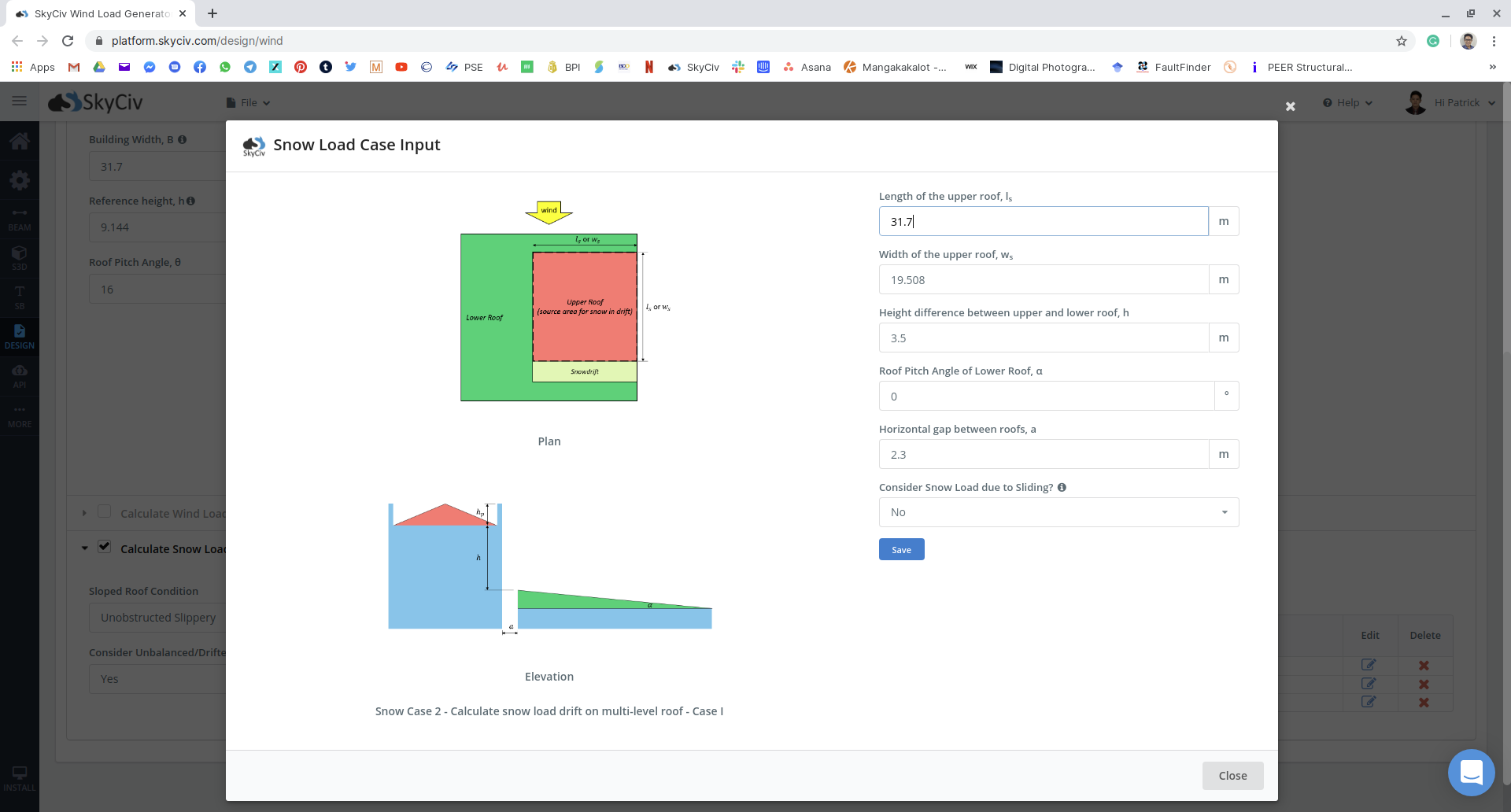
Figura 17: Entrada de carga de nieve para múltiples casos no balanceados para el ejemplo.
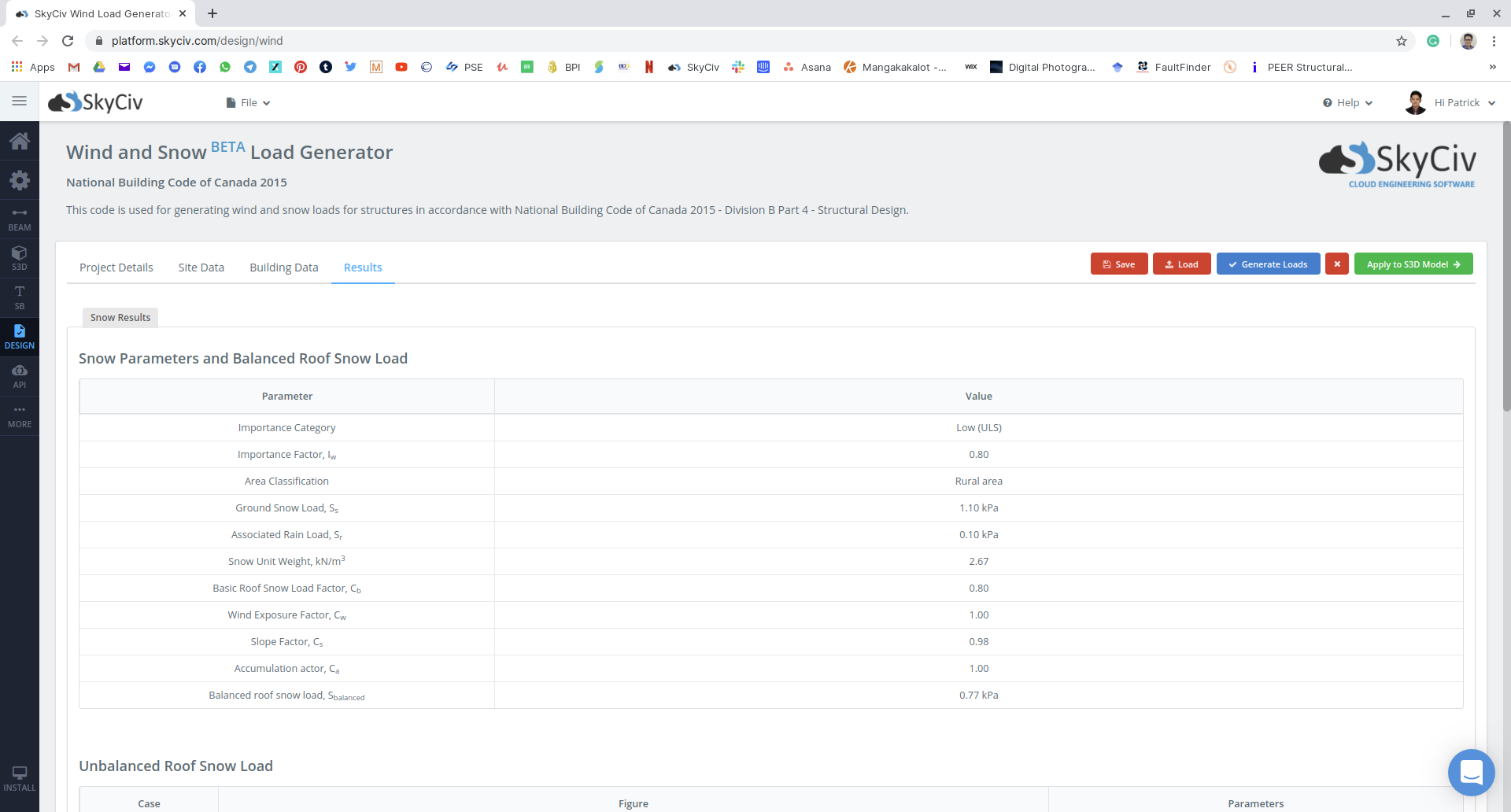
Figura 18: Resumen de los parámetros de carga de nieve utilizados y la carga de nieve equilibrada que se aplicará a la estructura.
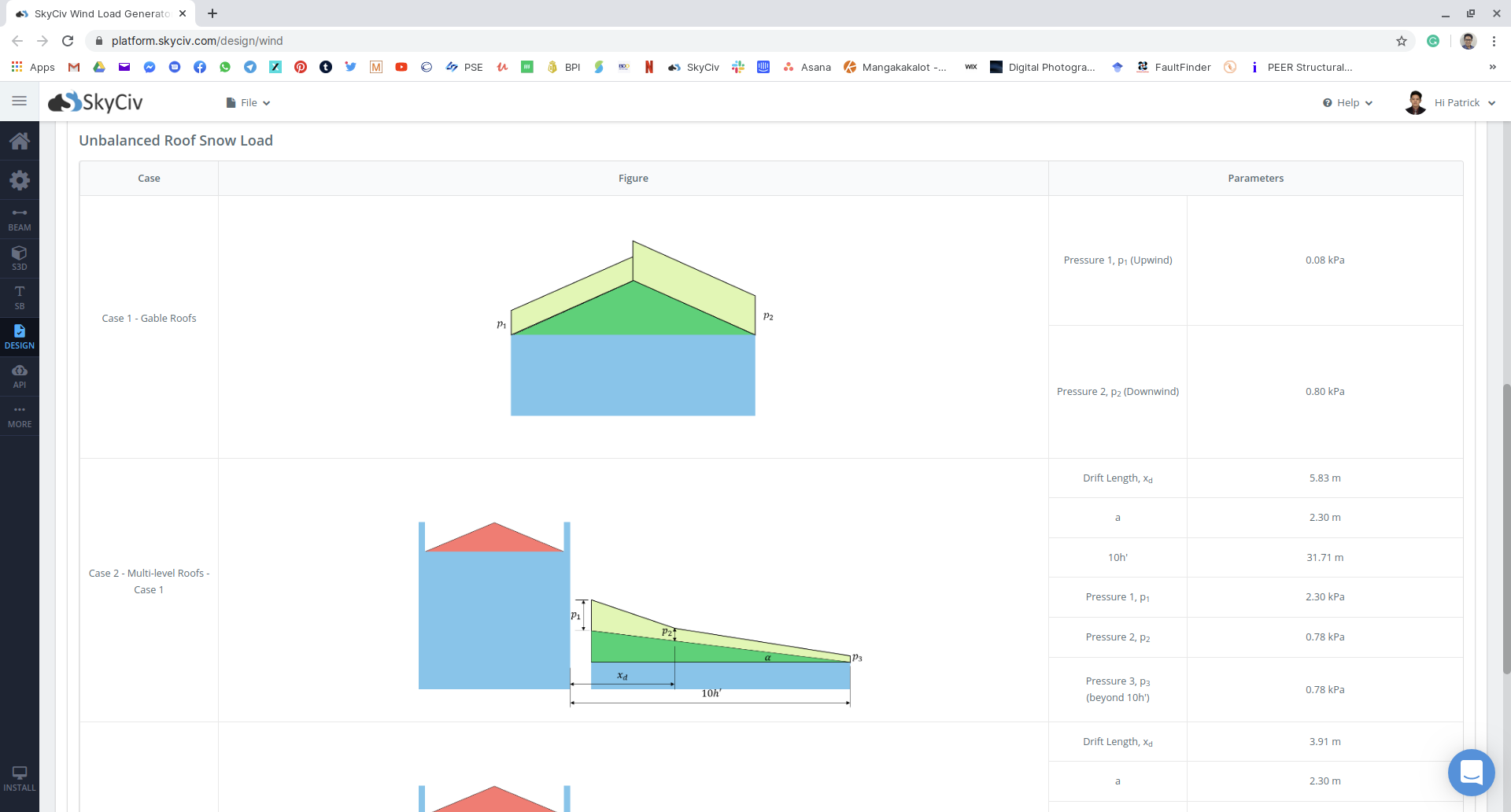
Figura 19: Resumen de resultados de carga de nieve desequilibrada.
Los cálculos de carga de nieve en el módulo del generador de carga SkyCiv están respaldados por códigos de referencia como ASCE 7-10, 7-16, EN 1991-1-3, NBCC 2015, y AS / NZS 1170.3, y está disponible en el Ser único (Solo generador de carga) y Profesional cuentas. Familiarizado con la programación y las API? Esta funcionalidad se puede automatizar con el uso de la SkyCiv API .
Ingeniero estructural, Desarrollo de Producto
Maestría en Ingeniería Civil
Referencias:
- Consejo Nacional de Investigaciones de Canadá. (2015). Código Nacional de Construcción de Canadá, 2015. Consejo Nacional de Investigaciones de Canadá.
Nota:
- Referencia del código NBCC para el “Factor básico de carga de nieve en el techo” — buscar 4.1.6.2 Frase (2)
- Referencia del código NBCC para el “Factor de exposición al viento” — buscar 4.1.6.2 Oraciones (3) y (4)
- Referencia del código NBCC para el “Factor de pendiente” — buscar 4.1.6.2 Oraciones (5), (6), y (7)
- Referencia del código NBCC para el “Factor de acumulación” — buscar 4.1.6.2 Frase (8), 4.1.6.5 para techos multinivel, 4.1.6.6 para tejados con hueco, y 4.1.6.9 para tejado a dos aguas



