Cómo calcular la capacidad de carga máxima de un solo pilote

Capacidad de carga

---

La evaluación de la capacidad de carga máxima de un solo pilote es uno de los aspectos más importantes del diseño del pilote., y a veces puede ser complicado. Este artículo recorrerá las ecuaciones que rigen el diseño de un solo pilote, así como un ejemplo..

Para comprender fácilmente el mecanismo de transferencia de carga de un solo pilote, imagina una pila de hormigón de longitud L con diámetro D, como se muestra en la figura 1.

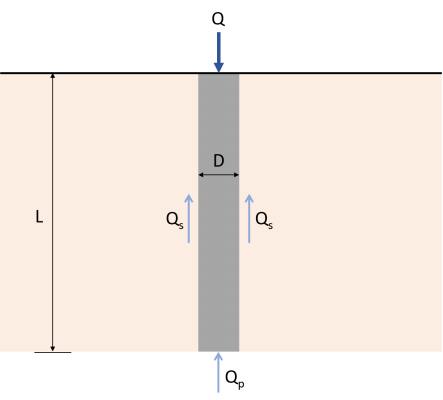
Figura 1: Mecanismo de transferencia de carga para pilotes

La carga Q aplicada sobre el pilote se transferirá directamente al suelo en la parte inferior del pilote.. Parte de esta carga será resistida por los lados del pilote usando algo llamado “fricción de piel” desarrollado a lo largo del eje (Q_s), y el resto será resistido por el suelo sobre el que se apoya el pilote (Q_pag). Por lo tanto, la máxima capacidad de carga (Qu) de una pila vendrá dado por la ecuación (1). Hay varios métodos disponibles para estimar los valores de Q_pag y Q_s.

\( {Q}_ _{tu} = {Q}_ _{pag} + {Q}_ _{s} \) (1)

Q_tu = Capacidad de carga máxima

Q_pag = Capacidad de carga del cojinete de extremo

Q_s = Resistencia a la fricción cutánea

¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta gratuita permite a los usuarios realizar cálculos de transporte de carga sin ninguna descarga o instalación.!

Calculadora de diseño de cimientos

Capacidad de carga final, Q_pag

---

La capacidad de carga final última es teóricamente la carga máxima por unidad de área que puede soportar el suelo en la carga., sin fallas. La siguiente ecuación de Karl Von Terzaghi, el padre de la mecánica del suelo, es una de las primeras y más utilizadas teorías para evaluar la capacidad portante última de las cimentaciones. La ecuación de Terzaghi para la capacidad de carga última se puede expresar como:

\( {q}_ _{tu} = (c × {norte}_ _{c}) + (q × {norte}_ _{q}) + (\frac{1}{2} × γ × B × {norte}_ _{C}) \) (2)

q_tu = Capacidad máxima de carga en los extremos

c = Cohesión del suelo

q = Presión efectiva del suelo

γ = Peso unitario del suelo

B = Profundidad o diámetro de la sección transversal

norte_c, norte_q, norte_C = Factores de apoyo

Dado q_tu es en términos de carga por unidad de área o presión, multiplicarlo por el área de la sección transversal del pilote dará como resultado la capacidad de carga de soporte final (Q_pag) de la pila. El valor resultante del último término de la ecuación 2 es insignificante debido a un ancho de pila relativamente pequeño, por lo tanto, puede eliminarse de la ecuación. Así, la capacidad de carga de carga final del pilote se puede expresar como se muestra en la ecuación (3). Esta versión modificada de la ecuación de Terzaghi se utiliza en el módulo SkyCiv Foundation al diseñar pilotes..

\( {Q}_ _{pag} = {A}_ _{pag} × [(c × {norte}_ _{c}) + (q × {norte}_ _{q}) ] \) (3)

A_pag = Área de la sección transversal del pilote

Factores de carga N_c y N_q son adimensionales, derivado empíricamente, y son funciones del ángulo de fricción del suelo (Fi). Los investigadores ya han completado los cálculos necesarios para encontrar factores de cojinete.. Tabla 1 resume los valores de N_q según el Comando de Ingeniería de Instalaciones Navales (NAVFAC DM 7.2, 1984). El valor de N_c es aproximadamente igual a 9 para pilotes bajo suelos arcillosos.

Factor de rodamiento (norteq)
Ángulo de fricción (Ø)	26	28	30	31	32	33	34	35	36	37	38	39	40
Pilotes conducidos	10	15	21	24	29	35	42	50	62	77	86	120	145
Montones aburridos	5	8	10	12	14	17	21	25	30	38	43	60	72

Tabla 1: norte_q valores de NAVFAC DM 7.2

Capacidad de resistencia a la fricción de la piel, Q_s

---

La resistencia a la fricción de la piel de los pilotes se desarrolla a lo largo del pilote.. Generalmente, la resistencia a la fricción de un pilote se expresa como:

\( {Q}_ _{s} = ∑ (p × ΔL × f) \) (4)

p = perímetro del pilote

ΔL = Longitud de pilote incremental sobre la que se toman p y f

f = Unidad de resistencia a la fricción a cualquier profundidad

Estimación del valor de la unidad de resistencia a la fricción. (F) requiere varios factores importantes a considerar, como la naturaleza de la instalación de pilotes y la clasificación del suelo. Ecuaciones (5) y (6) muestra el método computacional para encontrar la unidad de resistencia a la fricción de pilotes en suelos arenosos y arcillosos, respectivamente. Mesas 2 y 3 Presentar el coeficiente de presión de tierra efectivo recomendado (K) y el ángulo de fricción suelo-pilote (δ ’), según NAVFAC DM7.2.

Para suelos arenosos:

\( f = K × σ ’× tan(δ ’) \) (5)

K = coeficiente de presión de tierra efectiva

σ’ = Esfuerzo vertical efectivo a la profundidad considerada

D’ = Ángulo de fricción suelo-pilote

Para suelos arcillosos:

\( f = α × c \) (6)

α = factor de adherencia empírico

Ángulo de fricción suelo-pilote (δ ’)
Tipo de pila	D’
Pila de acero	20º
Pila de madera	3/4 × Φ
Pila de hormigón	3/4 × Φ

Tabla 2: Valores de ángulo de fricción de suelo-pilote (NAVFAC DM7.2, 1984)

Coeficiente de presión de tierra lateral (K)
Tipo de pila	Pila de compresión	Pila de tensión
Pilotes en H impulsados	0.5-1.0	0.3-0.5
Pilotes de desplazamiento impulsados (ronda, rectangular)	1.0-1.5	0.6-1.0
Pilotes de desplazamiento impulsados (afilado)	1.5-2.0	1.0-1.3
Pilotes impulsados ​​a chorro	0.4-0.9	0.3-0.6
Montones aburridos (<24″ Diámetro)	0.7	0.4

Tabla 3: Coeficiente de presión de tierra lateral (K) Valores (NAVFAC DM7.2, 1984)

Factor de adherencia (una)
c / pa	una
≤ 0.1	1.00
0.2	0.92
0.3	0.82
0.4	0.74
0.6	0.62
0.8	0.54
1.0	0.48
1.2	0.42
1.4	0.40
1.6	0.38
1.8	0.36
2.0	0.35
2.4	0.34
2.8	0.34

Nota: pag_a = presión atmosférica ≈ 100 kN / m²

Tabla 4: Valores del factor de adherencia (Terzaghi, Picotear, y Mesri, 1996)

Ejemplo: Calcular la capacidad de pilotes en arena.

---

Un pilote de hormigón de 12 metros de largo con un diámetro de 500 mm se introduce en múltiples capas de arena sin presencia de agua subterránea. Encuentre la máxima capacidad de carga (Q_tu) de la pila.

Detalles
Sección de
Diámetro	500 mm
Longitud	12 m
Propiedades del suelo de la capa 1
Grosor	5 m
Unidad de peso	17.3 kN / m3
Ángulo de fricción	30 Grados
Cohesión	0 kPa
Nivel freático	No presente
Propiedades del suelo de la capa 2
Grosor	7 m
Unidad de peso	16.9 kN / m3
Ángulo de fricción	32 Grados
Cohesión	0 kPa
Nivel freático	No presente

Paso 1: Calcule la capacidad de carga del cojinete del extremo (Q_pag).

En la punta de la pila:

A_pag = (π / 4) × D² = (π / 4) × 0.5²

A_pag = 0.196 m²

c = 0 kPa

θ = 32º

norte_q = 29 (De la tabla 1)

Presión efectiva del suelo (q):

q = (C₁ × t₁) + (C₂ × t₂) = (5 m × 17.3 kN / m³) + (7 m × 16.9 kN / m³)

q = 204.8 kPa

Luego usa la ecuación (3) para la capacidad de carga final:

Q_pag = A_pag × [(c × N_c) + (q × N_q)]

Q_pag = 0.196 m² × ( 204.8 KPa × 29)

Q_pag = 1,164.083 kN

Paso 2: Calcule la resistencia a la fricción de la piel (Q_s).

Usando ecuaciones (4) y (5), calcular la fricción de la piel por capa de suelo.

Q_s = ∑ (p × ΔL × f)

p = π × D = π × 0.5 m

p = 1.571 m

Capa 1:

ΔL = 5 m

F₁ = K × σ’₁× bronceado(δ ’)

K = 1.25 (Tabla 3)

D’ = 3/4 × 30º

D’ = 22,50º

σ’₁ = γ₁ × (0.5 × t₁) = 17.3 kN / m³ × (0.5 × 5 m)

σ’₁ = 43.25 kN / m²

F₁ = 1.25 × 43.25 kN / m² × bronceado(22.50º)

F₁ = 22.393 kN / m²

Q_s1 = p × ΔL × f₁ = 1.571 m × 5 m × 22.393 kN / m²

Q_s1 = 175.897 kN

Capa 2:

ΔL = 7 m

F₂ = K × σ’₂× bronceado(δ ’)

K = 1.25 (Tabla 3)

D’ = 3/4 × 32º

D’ = 24º

σ’₂ = (C₁ × t₁) + [C₂ × (0.5 × t₂)] = (17.3 kN / m³ × 5 m) + [16.9 kN / m³ ×(0.5 × 7 m)]

σ’₂ = 145.65 kN / m²

F₂ = 1.25 × 145.65 kN / m² × bronceado(24º)

F₂ = 81.059 kN / m²

Q_s2 = p × ΔL × f₂ = 1.571 m × 7 m × 81.059 kN / m²

Q_s2 = 891.406 kN

Resistencia total a la fricción cutánea:

Q_s = Q_s1+ Q_s2 = 175.897 kN + 891.406 kN

Q_s = 1,067.303 kN

Paso 3: Calcule la capacidad de carga máxima (Q_tu).

Q_tu = Q_pag+ Q_s = 1,164.083 kN + 1,067.303 kN

Q_tu = 2,231.386 kN

Ejemplo 2: Calcular la capacidad de pilotes en arcilla.

---

Considere un 406 pilote de hormigón de mm de diámetro con una longitud de 30 m incrustado en capas, arcilla saturada. Encuentre la máxima capacidad de carga (Q_tu) de la pila.

Detalles
Sección de
Diámetro	406 mm
Longitud	30 m
Propiedades del suelo de la capa 1
Grosor	10 m
Unidad de peso	8 kN / m3
Ángulo de fricción	0º
Cohesión	30 kPa
Nivel freático	5 m
Propiedades del suelo de la capa 2
Grosor	10 m
Unidad de peso	19.6 kN / m3
Ángulo de fricción	0º
Cohesión	0 kPa
Nivel freático	Completamente sumergido

Paso 1: Calcule la capacidad de carga del cojinete del extremo (Q_pag).

En la punta de la pila:

A_pag = (π / 4) × D²= (π / 4) × 0.406²

A_pag = 0.129 m²

c = 100 kPa

norte_c = 9 (Valor típico de la arcilla)

Q_pag = (c × N_c) × A_pag = (100 kPa × 9) × 0.129 m²

Q_pag = 116.1 kN

Paso 2: Calcule la resistencia a la fricción de la piel (Q_s).

Usando ecuaciones (4) y (6), calcular la fricción de la piel por capa de suelo.

Q_s = ∑ (p × ΔL × f)

p = π × D = π × 0.406 m

p = 1.275 m

Capa 1:

ΔL = 10 m

una₁ = 0.82 (Tabla 4)

c₁ = 30 kPa

F₁= α₁ × c₁ = 0.82 × 30 kPa

F₁ = 24.6 kN / m²

Q_s1 = p × ΔL × f₁ = 1.275 m × 10 m × 24.6 kN / m²

Q_s1 = 313.65 kN / m²

Capa 2:

ΔL = 20 m

una₂= 0.48 (Tabla 4)

c₂ = 100 kPa

F₂ = α₂ × c₂ = 0.48 × 100 kPa

F₂ = 48 kN / m²

Q_s2 = p × ΔL × f₂ = 1.275 m × 20 m × 48 kN / m²

Q_s2 = 1,224 kN / m²

Resistencia total a la fricción cutánea:

Q_s = Q_s1+ Q_s2 = 313.65 kN + 1224 kN

Q_s = 1,537.65 kN

Paso 3: Calcule la capacidad de carga máxima (Q_tu).

Q_tu = Q_pag+ Q_s = 116.1 kN + 1537.65 kN

Q_tu = 1,653.75 kN

¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta gratuita permite a los usuarios realizar cálculos de transporte de carga sin ninguna descarga o instalación.!

Calculadora de diseño de cimientos

Referencias:

• los, B.M. (2007). Principios de la ingeniería de cimientos (7a edición). Ingeniería global
• Rajapakse, R. (2016). Regla básica de diseño y construcción de pilotes (2nd edición). Elsevier Inc.
• Tomlinson, M.J. (2004). Práctica de diseño y construcción de pilotes (4a edición). E & FN Spon.