Los cimientos son un elemento esencial de una estructura para proporcionar estabilidad general al transmitir y distribuir las cargas totales de la estructura al suelo.. Cimientos poco profundos, como cimientos aislados rectangulares o cuadrados, son el tipo preferido de cimentación debido a la simplicidad de su construcción y costo total en comparación con las cimentaciones profundas. Estimar la presión base afecta dramáticamente el diseño y el tamaño de la zapata. Típicamente, la relación de utilidad entre la capacidad de carga permisible del suelo y la presión base gobernante debajo de la zapata es la base del tamaño inicial de la zapata. Una vez establecidas las dimensiones iniciales de la zapata, más controles de diseño para la seguridad y la estabilidad, como corte unidireccional y bidireccional, capacidad de flexión, y controles de longitud de desarrollo, se comprueban según el código de diseño que se utilice.

Cuando una zapata se somete a una flexión biaxial (M_x, M_z), se supone que la carga axial (PAG) actúa sobre una coordenada de excentricidad (mi_x, mi_z) donde hay una tendencia a girar desde el centro. La interacción entre el suelo y la zapata depende principalmente de la dimensión de la zapata y la excentricidad resultante de las cargas aplicadas.. Dependiendo de la ubicación de la excentricidad resultante, la presión base hace que la zapata esté en compresión total o parcial. En la práctica, se recomienda diseñar una zapata en compresión total. No se debe despreciar la compresión parcial o la pérdida de contacto entre el suelo y la zapata., pero la mayoría de los diseñadores evitan este escenario debido a su complejidad de cálculo. La zapata está en compresión total cuando la excentricidad resultante se encuentra dentro del núcleo o debajo de la Zona C. La excentricidad fuera de la Zona C pone la zapata en compresión parcial. Figura 1 muestra las diferentes zonas designadas en una base rectangular.

Este artículo se centrará en calcular las presiones en las esquinas bajo diferentes clasificaciones de zona basadas en Bellos. & Rastro (2017) y S.S.. de Ray (1995) estudios.

Clasificaciones de zonas de una zapata rectangular

Las clasificaciones de zona de una zapata rectangular se derivan de múltiples estudios realizados por diferentes autores para desarrollar un enfoque práctico para estimar la distribución de la presión del suelo en las condiciones de carga esperadas.. Como se muestra en la figura 1, hay cinco regiones diferentes (Zonas A-E) dependiendo de la ubicación de la excentricidad resultante. Cada zona corresponde a una carga diferente, distribución de presión base, y deformación. Zona C, también conocido como el núcleo, es el núcleo principal. Es la región ideal para diseñar una zapata, dando como resultado una compresión total en la zapata. Las dimensiones de esta región son equivalentes a 1/6 de su respectiva longitud de pie.

Figura 1: Clasificaciones de zonas de una zapata rectangular

 

El núcleo secundario es el área elíptica. (delimitado por la línea discontinua en la figura 1) con sus semiejes mayor y menor iguales a 1/3 de su respectiva longitud de pie. Esta región cubre la totalidad de las zonas B & C y algunas partes de las zonas D & E. El núcleo secundario da como resultado una compresión parcial de la zapata. Es una buena práctica mantener la excentricidad dentro de la zona secundaria para un diseño de zapata aceptable..

La excentricidad más allá de la zona secundaria es el resultado de una alta carga biaxial. Cubre toda la zona A y el resto de las zonas D & E. Se recomienda evitar diseñar la zapata en estas regiones ya que se corre el riesgo de volcar. Por lo tanto, es recomendable rediseñar las dimensiones de la zapata para este tipo de carga.

 

A continuación se enumeran las fórmulas analíticas para resolver las presiones de esquina en cada clasificación de zona.

Zona C (Núcleo principal, Zona de compresión completa)

Como se mencionó, este es el caso más preferido para diseñar zapatas ya que es capaz de comprimir toda la base de la zapata, como se muestra en la figura 2. Este caso está representado por una pequeña excentricidad dentro del kern o sin excentricidad. Figura 2 muestra la excentricidad dentro del núcleo con su máxima presión en las esquinas P3 & P4 y presión mínima en las esquinas P1 & P2.

Figura 2: Excentricidad (-mi_x, -mi_z) en la Zona C & área de compresión completa

Máximo & presiones mínimas en las esquinas (Bellos & Rastro, 2017):

 

 

Presiones en las esquinas basadas en la excentricidad
	PAG1	PAG2	PAG3	PAG4
+mix, +miz	PAGmax	PAGmax	PAGmin	PAGmin
+mix, -miz	PAGmax	PAGmax	PAGmin	PAGmin
-mix, -miz	PAGmin	PAGmin	PAGmax	PAGmax
-mix, +miz	PAGmin	PAGmin	PAGmax	PAGmax

Zona A (Zona de compresión triangular)

Este caso corresponde a cuatro áreas rectangulares en cada esquina de la zapata. Por lo general, ocurre con una gran excentricidad biaxial., imponiendo una alta área compresiva triangular en una de las esquinas, como se muestra en la región sombreada de la figura 3. Las esquinas restantes pierden contacto con el suelo.. Por lo tanto, este caso no es recomendable para el diseño.

Figura 3: Excentricidad (-mi_x, -mi_z) en la Zona A & área de compresión triangular alrededor de P3

 

Factor de seguridad recomendado para rodamiento (Bellos & Rastro, 2017):

 

 

Presiones en las esquinas basadas en la excentricidad
	PAG1	PAG2	PAG3	PAG4
mix(+), miz(+)	PAGmax	0	0	0
mix(+), miz(-)	0	PAGmax	0	0
mix(-), miz(-)	0	0	PAGmax	0
mix(-), miz(+)	0	0	0	PAGmax

Zona D (Zona de compresión trapezoidal)

La zona D también corresponde a grandes excentricidades en las áreas adosadas en la dirección x de la zapata, como se muestra en la figura 4. La excentricidad en la dirección z (mi_z) es mucho mayor que en la dirección x (mi_x). En este caso, dos esquinas de la zapata pierden contacto con el suelo y producen un área de compresión trapezoidal. En comparación con la zona A, que está completamente fuera de la zona secundaria, una porción de la zona D todavía está cubierta por la zona secundaria.

 

Figura 4: Excentricidad (-mi_x, -mi_z) en la Zona D & área de compresión trapezoidal alrededor de P3

 

Máximo & presiones mínimas en las esquinas (Bellos & Rastro, 2017):

 

 

 

Alturas verticales del área compresiva trapezoidal (Bellos & Rastro, 2017):

 

 

 

 

Presiones en las esquinas basadas en la excentricidad
	PAG1	PAG2	PAG3	PAG4
mix(+), miz(+)	PAGmax	0	0	PAGmin
mix(+), miz(-)	0	PAGmax	PAGmin	0
mix(-), miz(-)	0	PAGmin	PAGmax	0
mix(-), miz(+)	PAGmin	0	0	PAGmax

 

Zona E (Zona de compresión trapezoidal)

Similar a la zona D, este caso también produce un área de compresión trapezoidal pero es causada por una gran excentricidad en la dirección x(mi_x).

Figura 5: Excentricidad (-mi_x, -mi_z) en la Zona E & área de compresión trapezoidal alrededor de P3

 

Máximo & presiones mínimas en las esquinas (Bellos & Rastro, 2017):

 

 

 

Bases horizontales del área compresiva trapezoidal (Bellos & Rastro, 2017):

 

 

 

 

Presiones en las esquinas basadas en la excentricidad
	PAG1	PAG2	PAG3	PAG4
mix(+), miz(+)	PAGmax	PAGmin	0	0
mix(+), miz(-)	PAGmin	PAGmax	0	0
mix(-), miz(-)	0	0	PAGmax	PAGmin
mix(-), miz(+)	0	0	PAGmin	PAGmax

Zona B (Zona de compresión pentagonal)

Este caso se presenta cuando las cargas aplicadas sobre las zapatas generan una excentricidad moderada dentro de la zona secundaria. Las áreas cubiertas por la zona B están delimitadas por dos lados curvos y una base plana alrededor de los exteriores de la zona C. En este caso, se produce un área de compresión pentagonal, y solo una esquina de la zapata pierde contacto con el suelo. sin embargo, las soluciones proporcionadas a continuación son un poco complejas y requieren métodos de resolución numérica para las presiones de las esquinas y la x & y intersecciones del área de compresión.

Presiones de esquina (Bellos & Rastro, 2017):

 

 

 

Lados pentagonales del área compresiva (Bellos & Rastro, 2017):

 

 

 

 

 

Presiones en las esquinas basadas en la excentricidad
	PAG1	PAG2	PAG3	PAG4
mix(+), miz(+)	PAGmax	PAGq	0	PAGpag
mix(+), miz(-)	PAGpag	PAGmax	PAGq	0
mix(-), miz(-)	0	PAGpag	PAGmax	PAGq
mix(-), miz(+)	PAGq	0	PAGpag	PAGmax

 

Alternativamente, una solución más directa por S.S. Rayo (1995) se puede utilizar para las presiones de las esquinas y las intersecciones de la zona de compresión pentagonal. Las ecuaciones se dan a continuación.:

Presiones de esquina (SS. Rayo, 1995):

 

 

 

 

Lados pentagonales del área compresiva (SS. Rayo, 1995):

 

 

---

SkyCiv's Módulo de diseño de cimientos es capaz de resolver las presiones de base de una zapata rectangular de hormigón. Controles de diseño adicionales de acuerdo con diferentes códigos de diseño (ACI 318-14, estándar australiano 2009 & 2018, Eurocódigo, y estándares canadienses) también están disponibles.

Última actualización

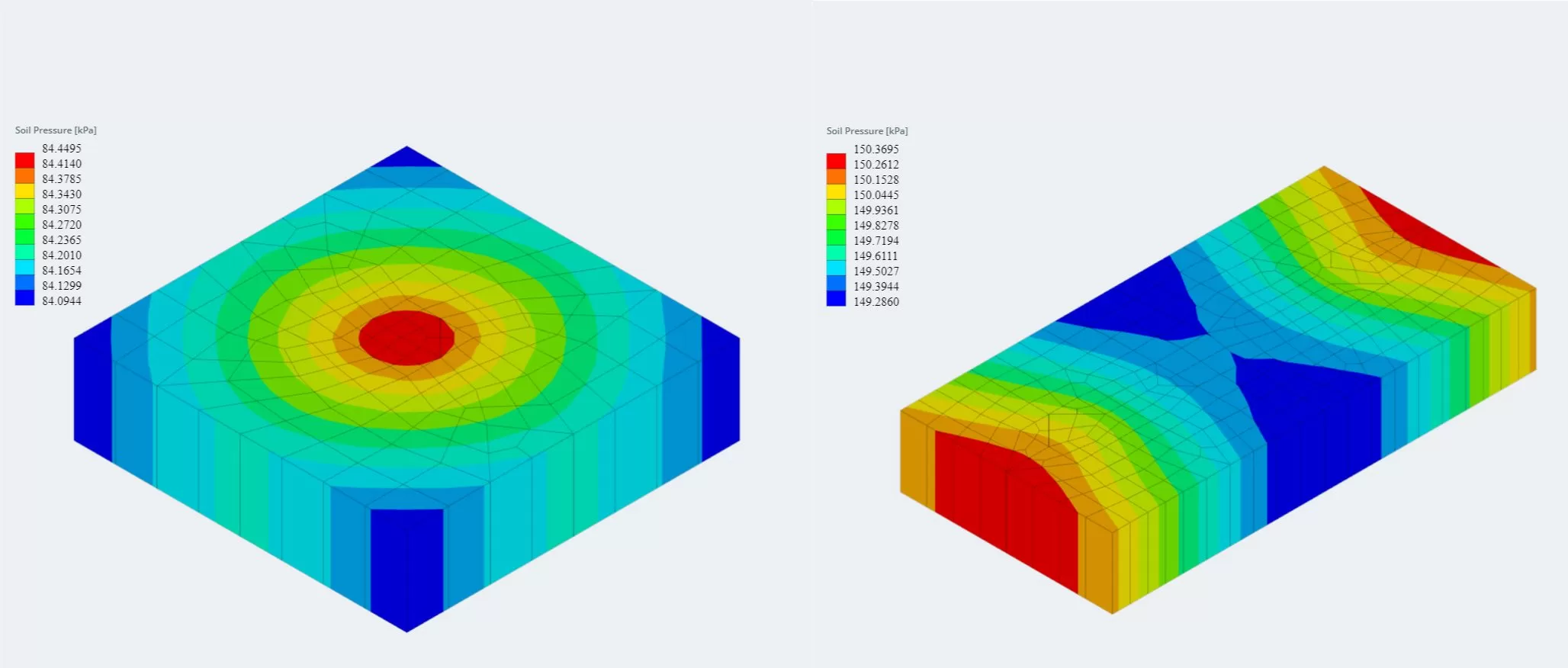
La última versión del módulo básico ahora está integrada con el Análisis de elementos finitos (FEA), que ofrece un análisis de presión del suelo más potente e introduce un análisis de armer de madera que se utilizará para una verificación de flexión mucho más detallada.. Los resultados de FEA para la presión del suelo y los momentos de armado de la madera se pueden ver en 3D y se agregaron a los informes..

 

¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta gratuita permite a los usuarios realizar cálculos de zapatas de concreto sin ninguna descarga o instalación!

Calculadora de pie de hormigón gratis

Referencias:

• Bellos, j, Rastro, norte. (2017). Solución analítica completa para la distribución lineal de la presión del suelo bajo zapatas rectangulares rígidas.
• los, B.M. (2007). Principios de la ingeniería de cimientos (7a edición). Ingeniería global
• Rawat, S., y. Alabama. (2020). Zapatas rectangulares aisladas bajo flexión biaxial: Una Metodología de Evaluación Crítica y Análisis Simplificado.
• Rayo, SS. (1995). Concreto reforzado. Ciencia de Blackwell