Tabla de Contenidos

• Vista general – ¿Cuál es el momento de inercia?
• Ejemplo – Cómo calcular el momento de inercia
• Fórmulas y ecuaciones
• Calculadoras
• Preguntas de práctica

Vista general – ¿Cuál es el momento de inercia??

En el contexto de la ingeniería estructural., El momento de inercia es una propiedad de la sección que se utiliza para determinar la capacidad de un elemento estructural para resistir fuerzas de flexión y torsión.. Suele ser un buen indicador de la rigidez y resistencia de las secciones bajo carga.. Un mayor momento de inercia significa que la estructura está mejor equipada para resistir la flexión y la deflexión., convirtiéndolo en un factor esencial en el diseño de vigas., columnas, y otros componentes portantes. Como curiosidad: A veces esto se define incorrectamente como segundo momento de inercia, sin embargo esto es incorrecto. Los otros nombres del momento de inercia son: momento de inercia del área, o segundo momento de zona.

Ejemplo – ¿Cómo calcular el momento de inercia de una sección de una viga?

Antes de encontrar el momento de inercia de una sección de viga (también conocido como segundo momento de área de una sección de viga), su centroide (o centro de masa) debe ser conocido. Por ejemplo, si el momento de inercia de la sección sobre su horizontal (XX) eje fue requerido entonces el vertical (y) centroide sería necesario primero (Por favor vea nuestros tutoriales calcular el centroide de una sección de viga y calcular el momento estático/primer momento de área).

Antes que empecemos, si estabas buscando nuestra Calculadora gratis de Momento Inercia haga clic en el enlace para obtener más información. Esto calculará el centroide, momento de inercia, y otros resultados e incluso mostrará los cálculos paso a paso! Pero por ahora, veamos una guía paso a paso y un ejemplo de cómo calcular el momento de inercia:

Paso 1: Segmente la sección de la viga en partes

Al calcular el área de momento de inercia, debemos calcular el momento de inercia de segmentos más pequeños. Intenta dividirlos en secciones rectangulares simples. Por ejemplo, considera la sección de I-beam a continuación, que también se presentó en nuestro tutorial de centroide. Hemos elegido dividir esta sección en 3 segmentos rectangulares:

 

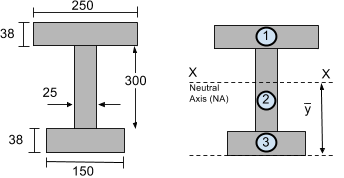
Paso 2: Calcular el eje neutro (EN)

El eje neutro (EN) o el eje horizontal XX está ubicado en el centroide o centro de masa. En nuestro tutorial de centroide, el centroide de esta sección se encontró previamente siendo 216.29 mm desde la parte inferior de la sección – esto está cubierto en nuestro cómo encontrar el centroide de una forma tutorial. Estos también se pueden calcular simplemente a partir de nuestra calculadora de centroide o ecuaciones de centroide.

Calculando el centroide, o eje neutro, es esencial en cómo calcular el momento de inercia de una viga, ya que este es el eje en el que actúa el momento de inercia.

Paso 3: Calcular Momento de Inercia

Para calcular el momento total de inercia de la sección, necesitamos usar el “Teorema del Eje Paralelo”:

Como lo hemos dividido en tres partes rectangulares, debemos calcular el momento de inercia de cada una de estas secciones. Es ampliamente conocido que el momento de inercia de la ecuación de un rectángulo sobre su eje centroide es simplemente:

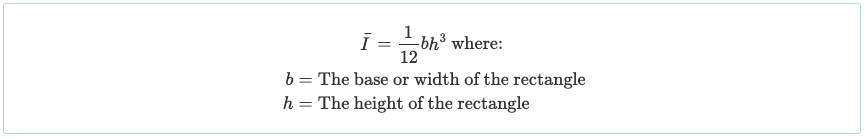
El momento de inercia de otras formas se indica a menudo en el inicio / reverso de los libros de texto o en esta guía del momento de inercia de formas. Sin embargo, la forma rectangular es muy común para las secciones de viga., entonces probablemente valga la pena memorizarla.

Ahora tenemos toda la información que necesitamos para usar el “Teorema del Eje Paralelo” y encontrar el momento total de inercia de la sección de viga en I. En nuestro momento de inercia ejemplo:

Ahí tienes nuestra guía para calcular el área de momento para secciones de viga. Este resultado es crítico en la ingeniería estructural y es un factor importante en la deflexión de una viga.. Esperamos que hayas disfrutado el tutorial y esperamos cualquier comentario que tengas. Para más información, visita nuestro tutorial en Momento de fórmula de inercia y ecuaciones.

Fórmulas y ecuaciones

Cada tipo de sección (rectangular, Viga en I, Circular) tiene su propia fórmula para un cálculo rápido. Estas son ecuaciones simplificadas que permiten a los ingenieros calcular rápida y fácilmente esta importante propiedad..

Las ecuaciones son una expresión simplificada de los pasos anteriores.. Por ejemplo, la fórmula para el momento de inercia de un rectángulo hueco es básicamente el MOI de la sección más grande – el más pequeño (interno) sección:

[math] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [math]

SkyCiv ha creado un recurso útil para usuarios comunes. Fórmula del momento de inercia.

Calculadoras

Hay muchas formas de calcular el momento de inercia, uno de los cuales es usar software para facilitar el proceso.

SkyCiv Section Builder es una herramienta de diseño de secciones totalmente capaz que va mucho más allá de la calculadora de momento de inercia. También te mostrará los cálculos paso a paso de cómo encontrar el momento de inercia.:

Alternativamente, puedes ver los resultados de nuestra Calculadora gratis de Momento Inercia para revisar tu trabajo. Esto calculará todas las propiedades de tu sección transversal y es una referencia útil para calcular el centroide, Area, y momento de inercia de las secciones de la viga! El beneficio adicional es que también puedes incluir el radio en las esquinas., para cálculos más precisos.

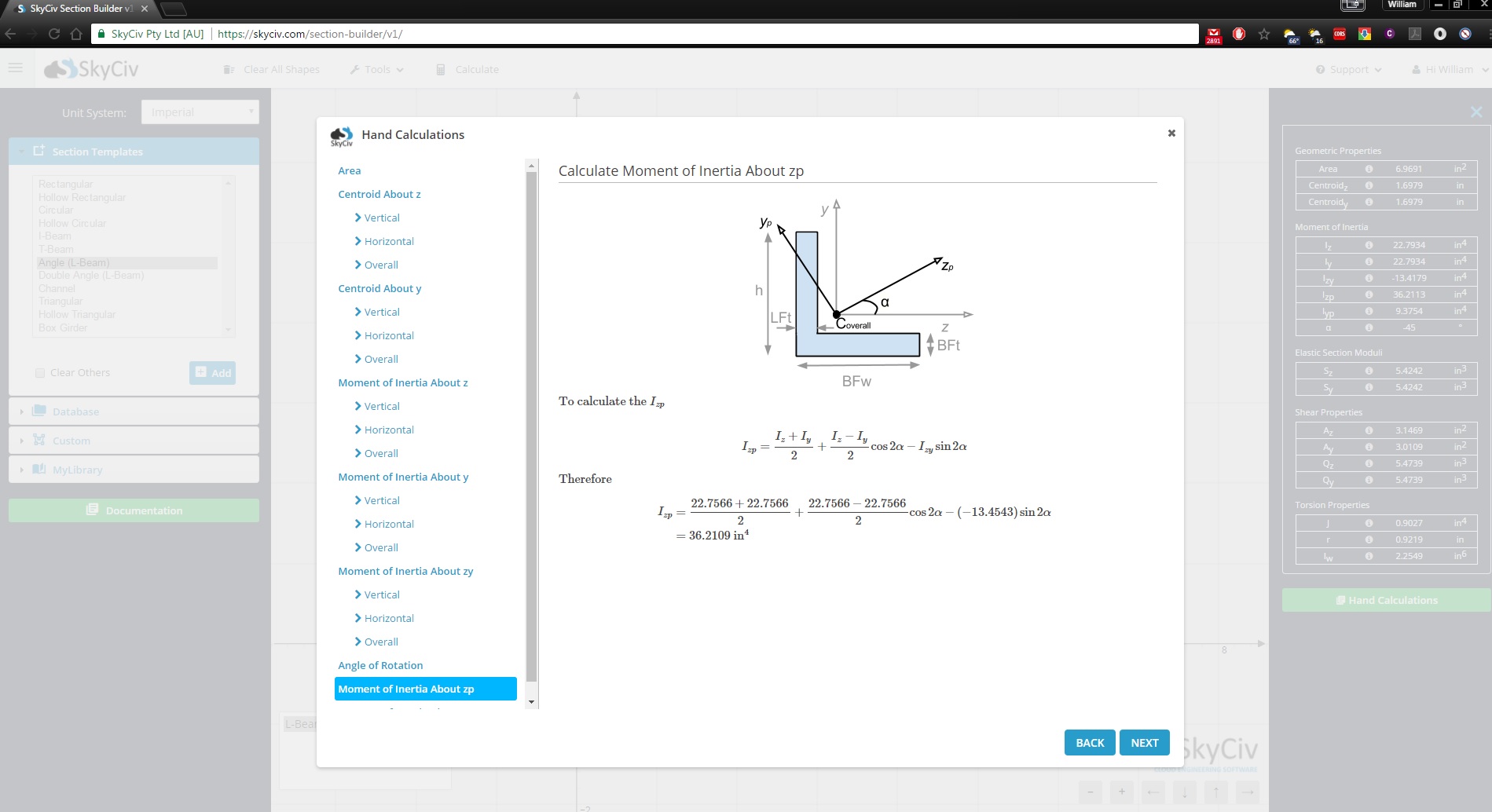
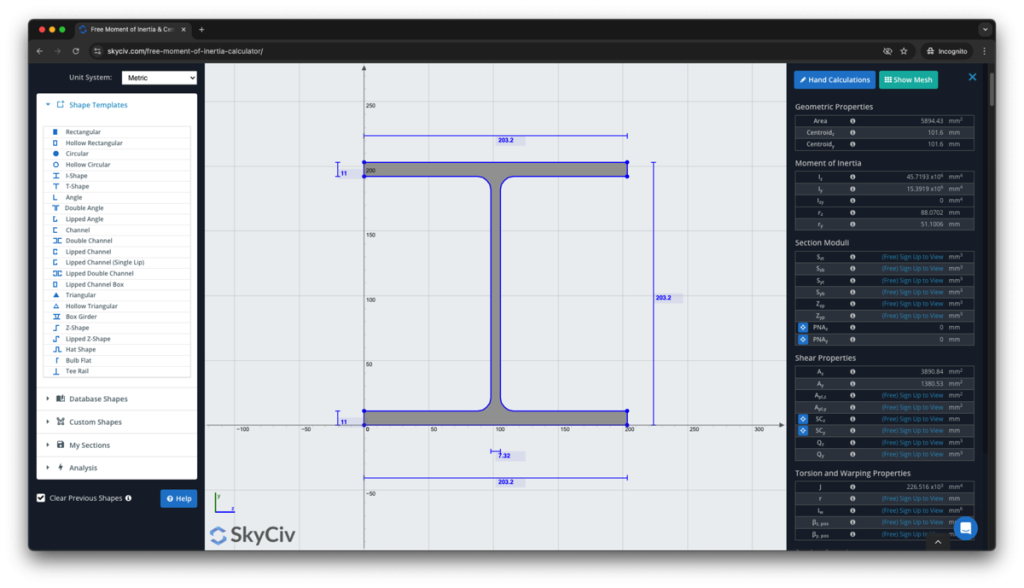
Regístrese hoy para explorar más sobre el software SkyCiv, o reserve una PRUEBA GRATIS para obtener asistencia con sus proyectos de ingeniería para usuarios existentes!

Adicionalmente, SkyCiv tiene un Calculadora de propiedades de sección como parte de la biblioteca de Diseño Rápido. Es una herramienta simplificada, pero también calculará el momento de inercia de formas de sección comunes.

Regístrate hoy

Preguntas de práctica

Pregunta 1: Sección rectangular

Problema: Calcular el momento de inercia. (Ixx y Iyy) para una sección rectangular con un ancho (b) de 200 mm y una altura (h) de 300 mm.

Solución: Las fórmulas para el momento de inercia de un rectángulo son:

[math] \dfrac{bh ^ 3}{12} [math]​

Sustituyendo los valores dados:

• ancho=200 mm
• altura=300 mm

Para Ixx:

[math] \dfrac{bh ^ 3}{12} = dfrac{200(300^ 3)}{12} = 450×10^6mm^4 ​ [math]​

Para Iyy:

[math] \dfrac{bh ^ 3}{12} = dfrac{300(200^ 3)}{12} = 200×10^6mm^4 ​ [math]​

Pregunta 2: Viga en I

Problema: Calcular el momento de inercia del eje mayor. (IXX) de una sección de viga I con las siguientes dimensiones:

• Ancho del ala superior (TFw) = 6 in
• Espesor del ala superior (TFt) = 0.43 in
• Profundidad de la sección = 6 in
• Grosor de la red (Wt) = 0.29 in
• Ancho del ala inferior (BFw) = 6 in
• Espesor del ala inferior (BFt) = 0.43 in

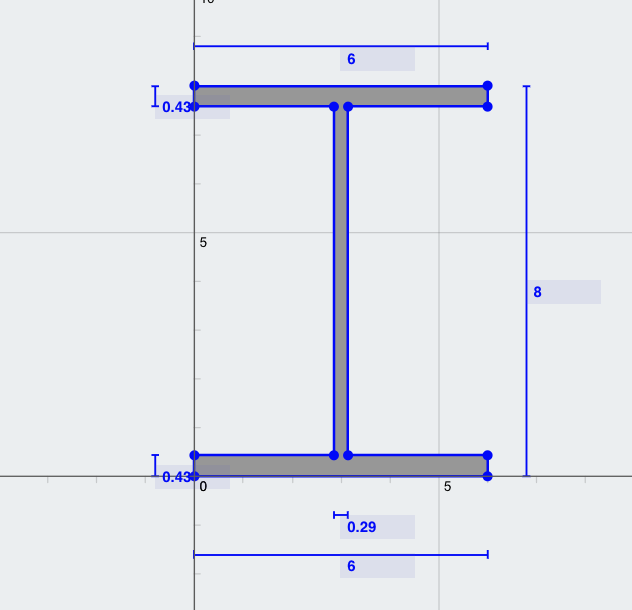
Solución:

[math] YO_{xx} = 82.8 en^4​ [math]​