Fundamentos del momento de inercia

El momento de inercia se puede derivar obteniendo el momento de inercia de las partes y aplicando la fórmula de transferencia: Yo = yo₀ + Anuncio². Tenemos un artículo completo que explica el enfoque para resolviendo el momento de inercia.

Fundamentalmente, el momento de inercia es el segundo momento del área, que se puede expresar como lo siguiente:

[math] YO_{x}= int int y ^{2}da [math] [math] YO_{y}= int int x ^{2}da [math]

Para observar la derivación de las fórmulas siguientes, intentamos encontrar el momento de inercia de un objeto como un rectángulo alrededor de su eje mayor usando solo la fórmula anterior. Para conseguir el momento de inercia, los límites deben determinarse de manera que se tomen desde el eje de rotación hasta su fibra extrema. Estos serían los límites de la integral externa. La integral interna tiene un límite de 0 a b. Eso dicho, también podemos expresar dA como xdy, que se convertirá en bdy. Como el eje de rotación está en el eje neutral, el momento de inercia se puede integrar con un límite superior de h / 2 y un límite inferior de 0 y multiplicado dos veces debido a la simetría del rectángulo. Esto nos deja con la integral a continuación.

[math] YO_{x}= 2 int_{0}^{\frac{h}{2}} y^{2}bdy [math] Integrando, [math] YO_{x}= 2b left [ \frac{y^{3}}{3} \verdad ]_ _{0}^{\frac{h}{2}} [math] [math] YO_{x}= 2b left [ \frac{h ^{3}}{24}-0 \verdad ] [math] [math] YO_{x}= frac{bh ^{3}}{12} [math]

Fórmula del momento de inercia para secciones de vigas

SkyCiv ha compilado un resumen de las ecuaciones de momento de inercia para secciones de viga (segundo momento de área). Las ecuaciones de momento de inercia son extremadamente útiles para cálculos rápidos y precisos. Las fórmulas se han resumido en sus formas más simples para su conveniencia..

SkyCiv también ofrece un Calculadora gratis de Momento Inercia para cálculos rápidos o para comprobar que ha aplicado la fórmula correctamente. La fórmula del momento de inercia para un rectángulo, circulo, Se han dado secciones de vigas huecas y triangulares.. Algunas cosas importantes para recordar con respecto al momento de inercia del área de una viga son:

• El momento de inercia del área es diferente del momento de inercia de la masa
• También se lo conoce como el segundo momento del área.
• Es un factor de deflexión significativo (cuanto mayor es el yo_x, la deflexión más baja será)
• Las unidades tienen una longitud equivalente a la potencia de 4
• Las siguientes ecuaciones dan el momento de inercia con respecto al centroide de la sección

REFERENCIA	Ixx	Iaa
Momento de la ecuación de inercia para secciones rectangulares o rectangulares
	[math] \dfrac{bh ^ 3}{12} [math]	[math] \dfrac{b ^{3}h}{12} [math]
Momento de la ecuación de inercia para una sección rectangular hueca
	[math] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [math]	[math] \dfrac{b ^ 3h}{12} – \dfrac{b_1 ^ 3h_1}{12} [math]
Momento de la ecuación de inercia para un círculo o sección circular
	[math] \dfrac{\pi}{64}D ^ 4 [math]	[math] \dfrac{\pi}{64}D ^ 4 [math]
Momento de la ecuación de inercia para una sección circular hueca
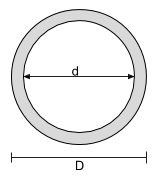	[math] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [math]	[math] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [math]
Momento de la ecuación de inercia para un triángulo isósceles
	[math] \dfrac{bh ^ 3}{36} [math]	[math] \dfrac{3b ^ 3h}{144} [math]
Momento de la ecuación de inercia de una sección en I
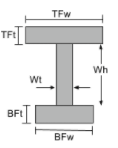	[math] \frac{TFw veces TFt ^{3}}{12} +\frac{Wt times Wh ^{3}}{12} + \frac{BFw times BFt ^{3}}{12} +[math] [math] TFw times TFt times left ( BFt + Wh + frac{TFt}{2} -\bar{y}_ _{larva del moscardón} \verdad )^{2} +[math] [math] Wt times Wh times left ( BFt + frac{Wh}{2} -\bar{y}_ _{larva del moscardón} \verdad )^{2} +[math] [math] BFw times BFt times left ( \frac{Wh}{2} -\bar{y}_ _{larva del moscardón} \verdad )^{2} [math]	[math] \frac{TFt veces TFw ^{3}}{12} + \frac{Wh times Wt ^{3}}{12} + \frac{BFt veces BFw ^{3}}{12} [math]
Momento de la ecuación de inercia de una sección en T
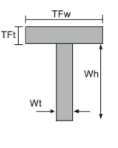	[math] \frac{TFw veces TFt ^{3}}{12} + \frac{Wt times Wh ^{3}}{12} +[math] [math] TFw times TFt left ( Wh + \frac{TFt}{2} -\bar{y}_ _{larva del moscardón} \verdad )^{2} +[math] [math] Wt times Wh times left ( \frac{Wh}{2} – \bar{y}_ _{larva del moscardón} \verdad )^{2} [math]	[math] \frac{TFt veces TFw ^{3}}{12} + \frac{Wh times Wt ^{3}}{12} [math]
Momento de la ecuación de inercia de una sección de canal
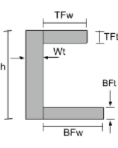	[math] \frac{TFw veces TFt ^{3}}{12} + \frac{BFw times BFt ^{3}}{12} + \frac{Peso veces h ^{3}}{12} +[math] [math] TFw times TFt times left ( h – \frac{TFt}{2} – \bar{y}_ _{larva del moscardón} \verdad )^{2} +[math] [math] BFw times BFt times left ( \frac{BFt}{2} – \bar{y}_ _{larva del moscardón} \verdad )^{2} +[math] [math] Wt times h times left ( \frac{h}{2} – \bar{y}_ _{larva del moscardón} \verdad )^{2} [math]	[math] \frac{TFt veces TFw ^{3}}{12} + \frac{BFt veces BFw ^{3}}{12} + \frac{h veces Wt ^{3}}{12} +[math] [math] TFt times TFw times left ( Wt + \frac{TFw}{2} – \bar{x}_ _{izquierda} \verdad )^{2} +[math] [math] BFt times BFw times left ( Wt + \frac{BFw}{2} – \bar{x}_ _{izquierda} \verdad )^{2} +[math] [math] h times Wt times left ( \frac{Wt}{2} – \bar{x}_ _{izquierda} \verdad )^{2} [math]
Momento de inercia Ecuación de ángulos
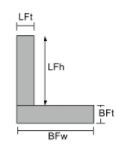	[math] \frac{BFw times BFt ^{3}}{12} + \frac{ LFt veces LFh ^{3}}{12} +[math] [math] BFw times BFt times left ( \frac{BFt}{2}-\bar{y}_ _{larva del moscardón} \verdad )^{2} +[math] [math] LFt times LFh times left ( BFt + \frac{LFh}{2}-\bar{y}_ _{larva del moscardón} \verdad )^{2} [math]	[math] \frac{BFt veces BFw ^{3}}{12} + \frac{ LFh veces LFt ^{3}}{12} +[math] [math] BFt times BFw times left ( \frac{BFw}{2}-\bar{x}_ _{izquierda} \verdad )^{2} +[math] [math] LFh times LFt times left ( \frac{LFt}{2}-\bar{x}_ _{izquierda} \verdad )^{2} [math]

Utilice SkyCiv Section Builder para cálculos manuales

En este artículo, lo hemos guiado a través de la fórmula del momento de inercia. Para más información sobre este tema, visita nuestro tutorial en Momento de inercia de la sección de la viga.

Sabías SkyCiv Section Builder también muestra los cálculos a mano completa para las siguientes formas?

• Rectangular, Rectangular Hueca
• Circular, Circular hueca
• Viga en I, Viga en T
• Ángulo (Viga en L), Canal
• Secciones triangulares

Esperamos que la tabla anterior le resulte útil para calcular el momento de inercia de un círculo., triángulo, y momento de inercia rectangular entre otras formas. También tenemos un útil Calculadora de Momento de Inercia, un simplificado de SkyCiv Section Builder, que maneja estos cálculos por usted o regístrese hoy para comenzar con el software SkyCiv!