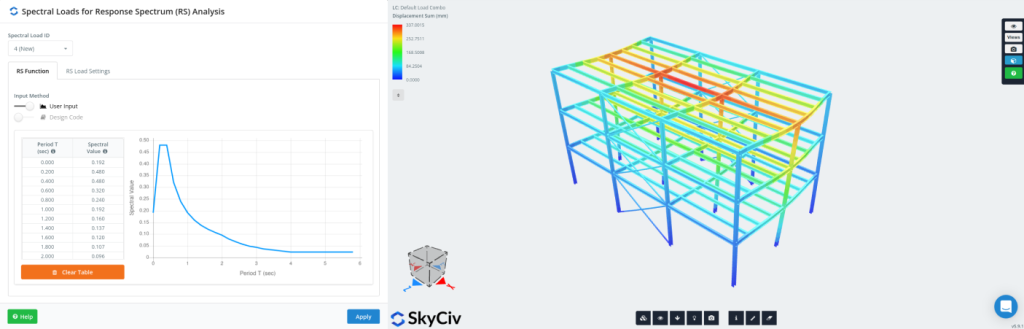
Al ejecutar un Análisis del espectro de respuesta en una estructura, uno de los pasos más importantes para obtener los resultados deseados es la definición del método de combinación modal que utilizará el software para obtener un resultado único para el desplazamiento, reacciones, fuerzas internas, etc.… para cada grado de libertad de los resultados brutos obtenidos para cada modo de vibración (respuestas modales). Esos resultados modales combinados son los que se utilizan para diseñar la estructura., es por eso que definir correctamente el método de combinación modal es extremadamente importante. En este artículo, nos sumergiremos en algunos métodos de combinación modal para el análisis del espectro de respuesta.
Es importante mencionar que uno de los pasos más importantes durante un Análisis de Espectro de Respuesta es la evaluación de la frecuencia natural para cada modo de vibración y su contribución de masa., consulte nuestra documentación sobre análisis dinámico de frecuencia.
Métodos de combinación modal para el análisis del espectro de respuesta
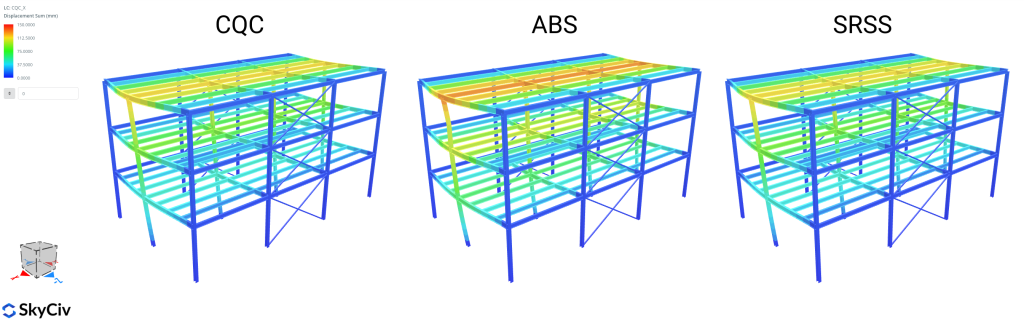
Algunos de los métodos más conocidos y utilizados para la combinación modal son:
- abdominales: suma absoluta
- SRSS: Raíz cuadrada de la suma de los cuadrados
- CQC: Combinación cuadrática completa
En general, valores pico de la respuesta total (\(r_o)) para desplazamientos, fuerzas internas, y las reacciones son de interés. Como se mencionó anteriormente, ese valor máximo se obtiene al combinar adecuadamente las respuestas modales máximas (\(r_{norte, los}\))
suma absoluta (abdominales)
El método de combinación modal Absolute Sum toma el valor absoluto del resultado (desplazamiento o fuerza interna) para cada modo de vibración y suma todos esos valores absolutos. Físicamente, asume que todas las respuestas modales máximas ocurren al mismo tiempo. Haciendo eso, es el método más conservador, ya que hace que cada contribución modal sea positiva, y por lo tanto, no es popular en aplicaciones de diseño estructural. La fórmula para calcular el valor pico de la respuesta total es:
\(r_o=\sum_{n=1}^{norte} |r_{norte,los}|\)
Dónde,
\(n\) es el \(n^{th}\) modo de vibración considerado en el análisis
\(N\) es el número total de modos de vibración considerados en el análisis
\(r_o) es la respuesta total pico
\(r_{norte,los}\) es la respuesta modal pico para el \(n^{th}\) modo de vibración
Raíz cuadrada de la suma de los cuadrados (SRSS)
El método de combinación modal de la raíz cuadrada de la suma de los cuadrados toma la raíz cuadrada de la suma de los cuadrados del resultado para cada modo de vibración, proporcionando una estimación del pico de la respuesta total. Este método de combinación modal proporciona excelentes estimaciones de respuesta para estructuras con frecuencias naturales bien separadas, para los casos en los que las frecuencias naturales de la estructura no estén bien separadas, no se debe utilizar este método. Formalmente, la respuesta total máxima se puede expresar de la siguiente manera:
\(r_o=\left(\flexion en vigas por el metodo de area de momentos{n=1}^{norte} r^{2}_ _{norte,los}\verdad)^{1/2}\)
Dónde,
\(n\) es el \(n^{th}\) modo de vibración considerado en el análisis
\(N\) es el número total de modos de vibración considerados en el análisis
\(r_o) es la respuesta total pico
\(r_{norte,los}\) es la respuesta modal pico para el \(n^{th}\) modo de vibración
Combinación cuadrática completa (CQC)
El método de Combinación Cuadrática Completa supera la limitación mencionada para SRSS al combinar respuestas modales en una estructura con frecuencias naturales muy próximas. En este método, la respuesta total máxima se obtiene aplicando la siguiente fórmula:
\(r_o=\left(\flexion en vigas por el metodo de area de momentos{i = 1}^{norte}\flexion en vigas por el metodo de area de momentos{n=1}^{norte} \rho_{in} \cdot r_{yo} \cdot r_{No} \verdad)^{1/2}\)
Dónde,
\(norte, \; i\) es el \(n^{th}, \; yo^{th}\) modo de vibración considerado en el análisis
\(N\) es el número total de modos de vibración considerados en el análisis
\(r_o) es la respuesta total pico
\(r_{norte,los}, \; r_{i,los}\) es la respuesta modal pico para el \(n^{th}, \; yo^{th}\) modo de vibración
\(\rho_{in}\) es el coeficiente de correlación para los dos modos que se combinan en cada paso de suma
La fórmula anterior se puede reescribir como dos grupos separados de sumas, siendo el primero idéntico al método de combinación modal SRSS. La segunda sumatoria doble incluye toda la cruz. (\(i \neq n\)) condiciones, cada uno de los cuales puede ser positivo o negativo, esto produce el hecho de que la estimación de la respuesta total máxima utilizando CQC podría ser mayor o menor que la estimación proporcionada por el SRSS :
\(r_o=\left( \flexion en vigas por el metodo de area de momentos{n=1}^{norte} r^{2}_ _{norte,los} + \refuerzo inferior{\flexion en vigas por el metodo de area de momentos{i = 1}^{norte}\flexion en vigas por el metodo de area de momentos{n=1}^{norte}}_ _{i \neq n} \rho_{in} \cdot r_{yo} \cdot r_{No} \verdad)^{1/2}\)
Solo un término en la ecuación para CQC no ha sido definido: el coeficiente de correlación. Una de las ecuaciones más utilizadas para este coeficiente es:
\(\rho_{in} = frac{\xi^2(1+\beta_{in})^ 2}{(1-\beta_{in})^2+4\xi^2\beta_{in}}\)
Dónde,
\(\beta_{in}\) es la relación entre las frecuencias naturales de los \(yo^{th}\) y \(n^{th}\) modos (\(\omega_i / \omega_n\))
\(\xi) es el coeficiente de amortiguamiento de la estructura
Referencias
Chopra, A. (2015, junio 4). Dinámica de Estructuras (4El d.). Educación superior Pearson.
Nuevo en SkyCiv Estructural 3D? Inscríbete hoy gratis!
Desarrollador de producto
BEng (Civil)



