Tutorial: Cómo resolver una estructura de armadura utilizando el método de secciones

En este tutorial, exploraremos y aprenderemos los beneficios de usar el Método de las Secciones para resolver su estructura de truss. ¿Qué son las armaduras?? Si no estás seguro de esto, visita nuestro ¿Qué es un braguero? artículo. El método de secciones se utiliza para resolver estructuras de celosía más grandes de forma rápida., manera simple. Implica tomar un corte ‘’ a través de una serie de miembros para evaluar sus fuerzas axiales y usar esto como nuestra base para resolver el resto de la estructura del truss.

la gran cosa es, Armadura SkyCiv hace esto automáticamente por ti. Modele sus propios trusses y el software le mostrará paso a paso de forma interactiva el método de las secciones!

Ver el videotutorial

Pregunta de muestra

Para nuestro ejemplo resuelto, estaremos viendo la siguiente pregunta:

Pregunta: Usando el método de secciones, determinar las fuerzas en los miembros 10, 11, y 13 de la siguiente estructura de celosía:

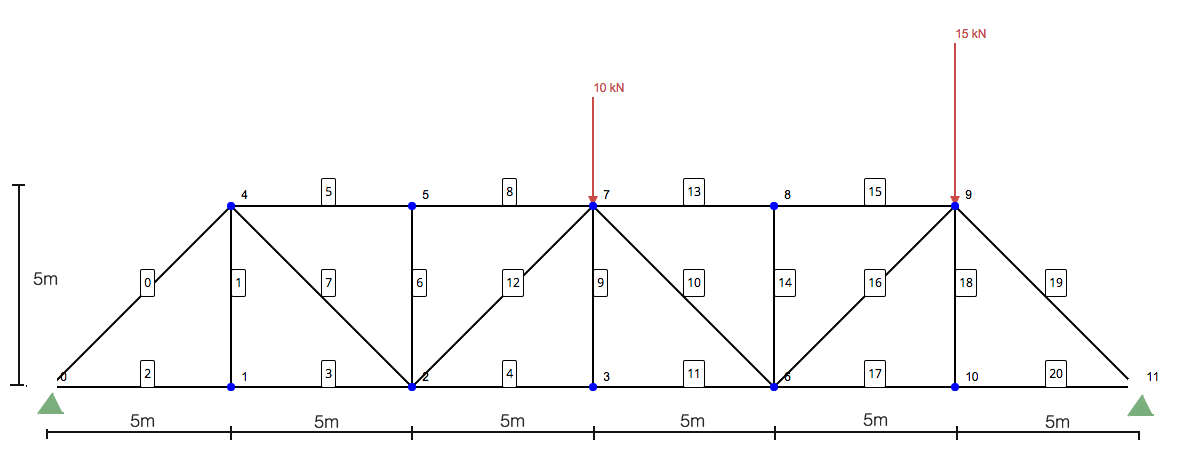
Paso 1: Calcular las reacciones a los soportes

Como la mayoría de los análisis estructurales estáticos, primero debemos empezar por localizar y resolver el reacciones en soportes. Esto nos dará las condiciones de contorno que necesitamos para progresar en la resolución de la estructura de celosía.. Simplificando la estructura para incluir solo las cargas y soportes:

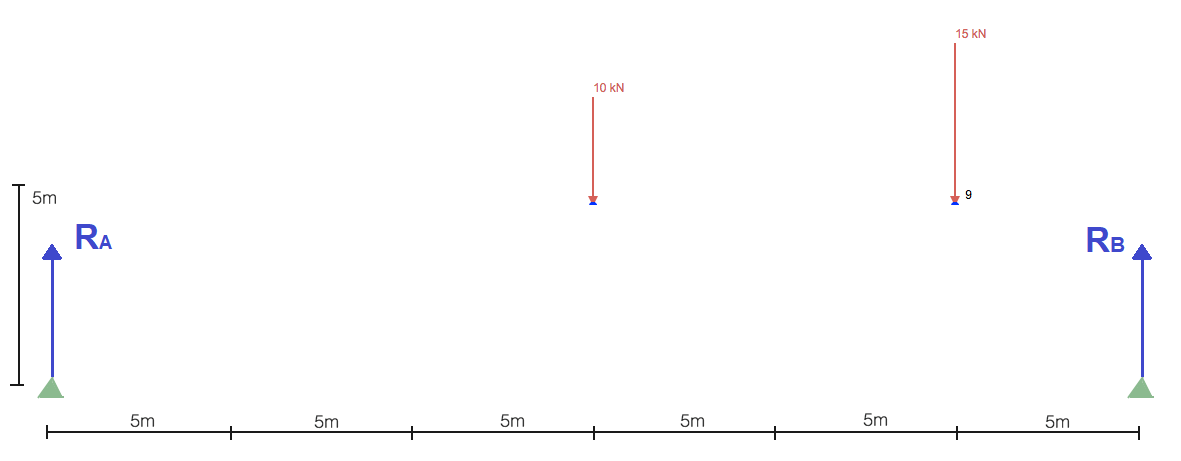
Sin perder demasiado tiempo calculando las reacciones, generalmente comienzas tomando la suma de momentos sobre un punto. Tomar la suma de momentos sobre el soporte izquierdo nos lleva:

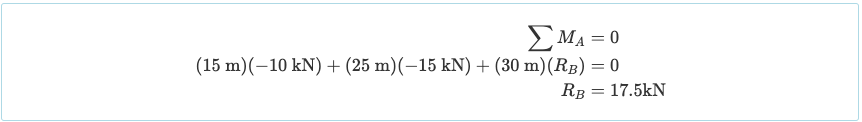
Entonces la reacción en el soporte correcto (R_B) es 17.5 kN en una dirección ascendente. Ahora, tomando la suma de fuerzas en el y nos da la reacción R_A como 7.5kN en una dirección ascendente:

Paso 2: Haga un corte a lo largo de los miembros de interés.

Aquí viene la parte más importante de resolver una armadura usando el método de las secciones. Implica hacer un corte a través de los miembros que desea resolver. Este método de análisis estructural es extremadamente útil cuando se intenta resolver algunos de los miembros sin tener que resolver toda la estructura mediante el método de juntas.. Entonces, en nuestro ejemplo aquí sería nuestro segmento:

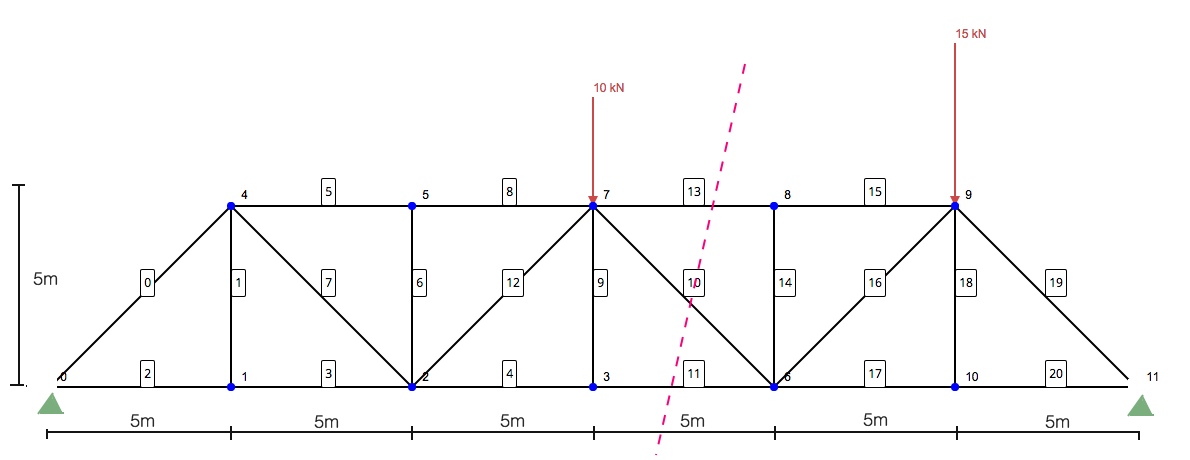
Enfocando solo en el lado izquierdo, te queda la siguiente estructura:

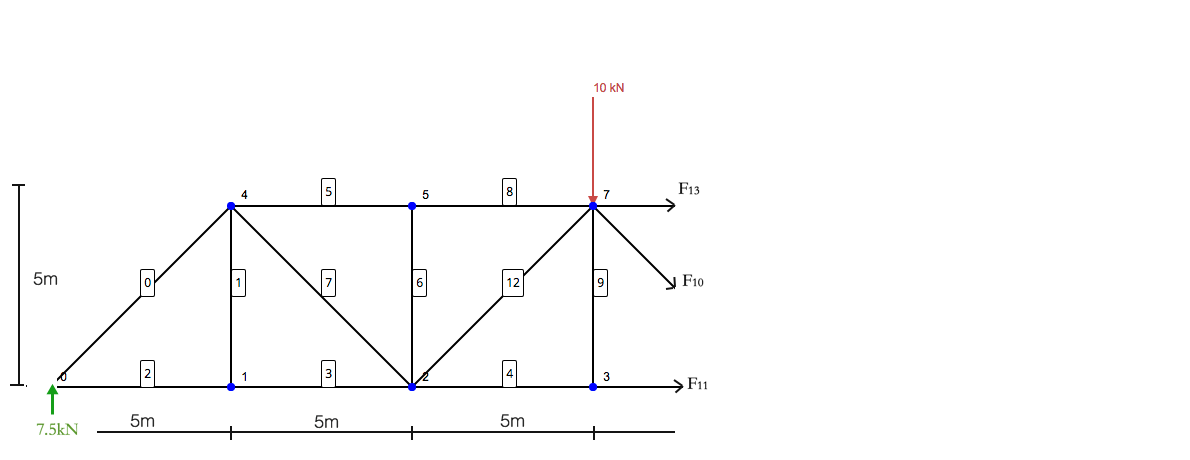
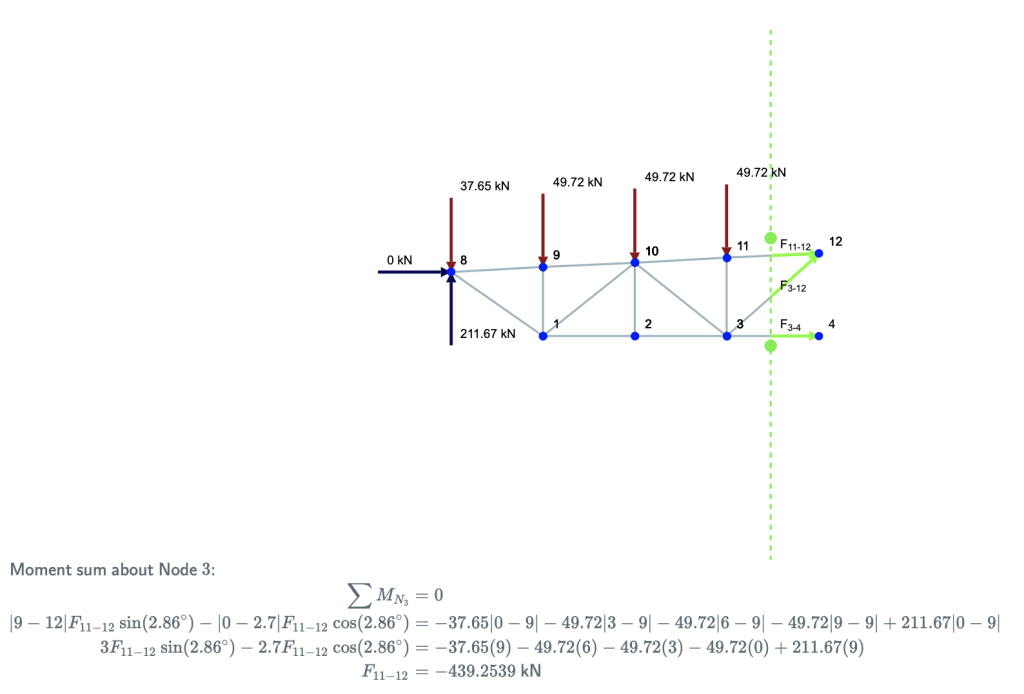
Ahora piense en esta estructura como una estructura de pie único. Las leyes de la estática todavía se aplican. – entonces la suma de momentos y fuerzas debe ser igual a cero. Los miembros con flechas (F₁₃, F₁₀, F₁₁) son los que estabilizan la reacción y las fuerzas aplicadas a la estructura. Tenga en cuenta que la suma de momentos se toma sobre el nodo 7 – como excluiría las fuerzas de los miembros 13 y 10 – dejando F₁₁ estar aislado.

Usando el diagrama de cuerpo libre anterior, podemos obtener las siguientes fórmulas:

Suma de fuerzas en la dirección y:

[math]
\empezar{alinear}
+\flecha arriba text{ } \suma{F_y} &= 0\\
7.5\texto{ kN} – 10 \texto{ kN} – F_{10}sin(45^{\circo}) &= 0\\
F_{10} &= -3.536 \texto{ kN}
\final{alinear}
[math]

Suma de momentos sobre el nodo 7:

[math]
\empezar{alinear}
+\círculoflechaizquierda text{ } \suma{M_7} &= 0\\
-(15 \texto{ m})(7.5 \texto{ kN}) + (5 \texto{ m})F_{11} &= 0\\
F_{11} &= 22.5 \texto{ kN}
\final{alinear}
[math]

Suma de fuerzas en la dirección x:

[math]
\empezar{alinear}
+\flecha derecha text{ } \suma{F_x} &= 0\\
F_{13} + F_{11} + F_{10}cos(45^{\circo}) &= 0\\
F_{13} &= -F_{11} – F_{10}cos(45^{\circo}) \\
F_{13} &= – (22.5 \texto{ kN}) – (-3.536 \texto{ kN})cos(45^{\circo}) \\
F_{13} &= -22.5 \texto{ kN} + (3.536 \texto{ kN})cos(45^{\circo}) \\
F_{13} &= -20 \texto{ kN}
\final{alinear}
[math]

Solución final

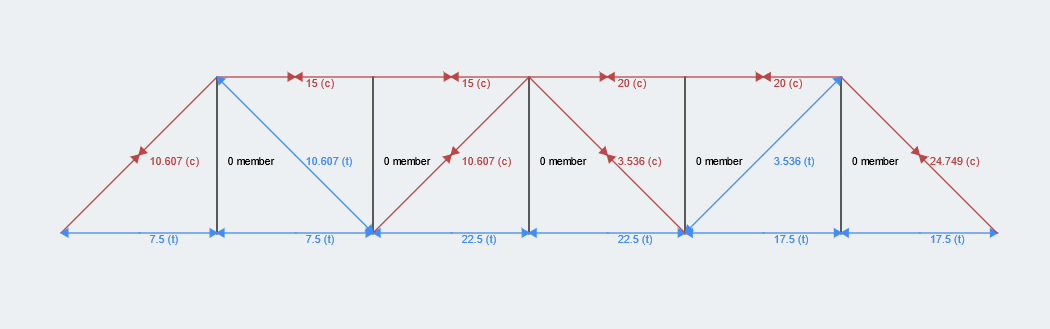
Podemos usar estos resultados para resolver los miembros restantes en la estructura de celosía. Esperamos que este ejemplo de cálculo de truss haya sido útil y no dude en comentar sus preguntas a continuación.. Como una referencia, Los resultados para toda la estructura Truss se pueden encontrar a continuación. (usando nuestro Calculadora de Armaduras) lo cual es genial para verificar tus respuestas!

Resumen de pasos

• Comience siempre calculando las reacciones en los soportes
• Haz un corte a través de los miembros que deseas resolver
• Trate la media estructura como su propia armadura estática
• Resuelve la armadura tomando la suma de fuerzas = 0
• Tómese el momento sobre un nodo de más de un miembro desconocido

Software SkyCiv Truss

Esperamos que este tutorial te haya resultado útil para tus proyectos.. Visita nuestro tutoriales de armadura para obtener más información útil sobre truss y no olvide consultar nuestro guía para resolver truss por el método de juntas.

Armadura SkyCiv puede calcular el método de las secciones automáticamente para usted. O prueba nuestro Calculadora Gratuita de Cerchas que te dará la respuesta final (sin cálculos manuales).

Para explorar más funciones del software SkyCiv, Regístrese hoy para comenzar!

Empiece gratis