Cómo calcular el factor de seguridad contra el deslizamiento de un muro de contención – Ejemplo de cálculo del momento de vuelco
Este ejemplo de cálculo del deslizamiento de un muro de contención es una guía sencilla sobre cómo calcular el factor de seguridad contra el deslizamiento en un muro de contención como parte de las comprobaciones de estabilidad.. Este ejemplo de cálculo del deslizamiento de un muro de contención es una guía sencilla sobre cómo calcular el factor de seguridad contra el deslizamiento en un muro de contención como parte de las comprobaciones de estabilidad.. Básicamente, Este ejemplo de cálculo del deslizamiento de un muro de contención es una guía sencilla sobre cómo calcular el factor de seguridad contra el deslizamiento en un muro de contención como parte de las comprobaciones de estabilidad..
Eso dicho, Ejemplo de cálculo del momento de vuelco:
Ejemplo de cálculo del momento de vuelco:
Ejemplo de cálculo del momento de vuelco
- Altura: 3.124 m
- Anchura: 0.305 m
- Compensar: 0.686 m
Base
- Anchura: 2.210 m
- Grosor: 0.381 m
Ejemplo de cálculo del momento de vuelco
- Ejemplo de cálculo del momento de vuelco: 18.85 kN / m3
- Ángulo de fricción: 35 grados
Subestructura Suelo
- Ejemplo de cálculo del momento de vuelco: 18.85 kN / m3
- Ángulo de fricción: 35 grados
- Coeficiente de fricción suelo-concreto: 0.55
- Presión de rodamiento admisible: 143.641 kPa
capas de suelo:
- Activo: 3.505 m
- Pasivo: 0.975 m
- Infraestructura: 0.792 m
Valor de carga de recargo: -17.237 kN / m
Todas las cargas asociadas con el Cálculo de Deslizamiento de Muro de Contención se muestran en la siguiente imagen:
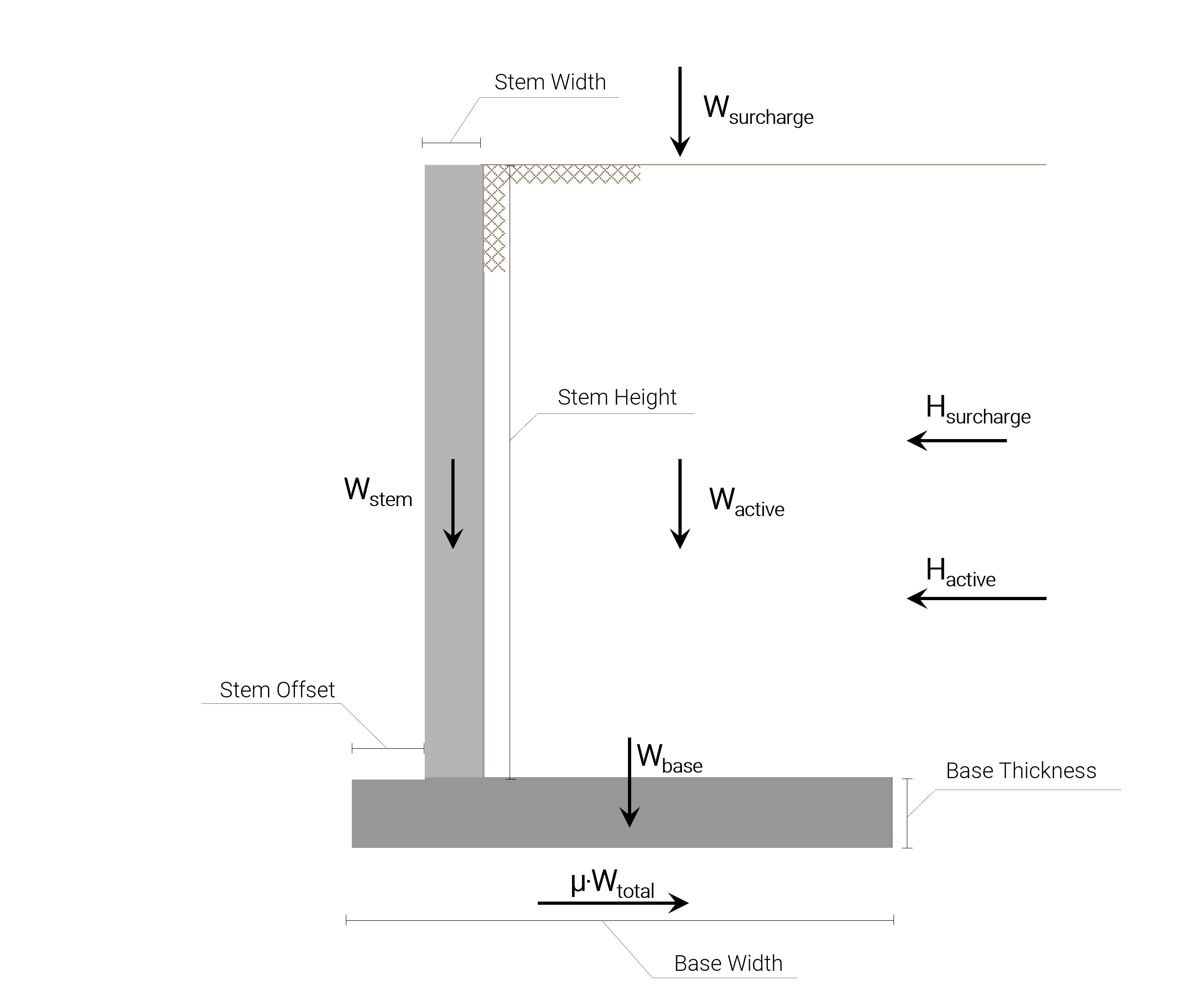
fuerza de deslizamiento
Como se mencionó, la fuerza de deslizamiento es la suma de la fuerza horizontal resultante de la presión activa del suelo en el lado del suelo activo y la fuerza horizontal resultante de la presencia de la sobrecarga.
se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales, se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales:
\( K_a = frac{1-\sin(\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{suelo,\;activo})}{1+\sin(\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{suelo,\;activo})} \)
\( K_a = frac{1-\sin(35º)}{1+\sin(35º)} = 0.271 \)
se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales, se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales:
\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo} = frac{1}{2} \cdotgamma_{suelo,\;activo} \cdot (madre_{la altura} + base_{grosor})^{2} \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales \)
\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo} = frac{1}{2} \cdot 18.85\;kN/m^3 cdot 3,505^{2} \cdot 0.271 \)
\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo} = 31.377\;kN / m \)
Para el cálculo de la fuerza horizontal relacionada con la presencia de sobrecarga, primero se calcula una altura equivalente del suelo, y luego la fuerza real:
\( h_{suelo,\;equivalente} = frac{recargo_{valor}}{\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{suelo,\;activo}} = frac{17.237 \;kN / m}{17.237 \;kN / m} \)
\( h_{suelo,\;equivalente} = 0.914 \; m \)
\( se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} = \gamma_{suelo,\;activo} \cdot h_{suelo,\;equivalente} \cdot (madre_{la altura} + base_{grosor}) \cdot K_a\)
\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} =\cdot 18.85\;kN/m^3 cdot 0.914 \; m cdot 3.505 \; m cdot 0.271 \)
\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} = 16.372\;kN / m \)
Con esas dos cargas calculadas, ahora es posible calcular la fuerza de deslizamiento sumando las dos cargas:
\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{H} = H_{activo} + se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} = 31.377\;kN / m + 16.372\;kN / m \)
\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{H} = 47.749 \; kN \)
Fuerza de fricción
Para calcular la fuerza de rozamiento que resiste la fuerza de deslizamiento, es necesario evaluar primero la carga vertical total:
\(W_{madre} = gamma_{hormigón} \cdot (madre_{la altura} \tallo cdot_{anchura} ) = 23.58 \;kN/m^3 cdot 3.124\;m cdot 0.305\;metro)
\( W_{madre}= 22.467\;kN/m)
\(W_{base} = gamma_{hormigón} \cdot (base_{grosor} \cdot base_{anchura} ) = 23.58 \;kN/m^3 cdot 0.381\;m cdot 2.210\;metro)
\( W_{base}= 18.855\;kN/m)
\(W_{activo} = gamma_{suelo,\;activo} \cdot (madre_{la altura}\cdot (base_{anchura}-madre_{compensar}-madre_{anchura}) ) \)
\( W_{activo} = 18.85 \;kN/m^3 cdot 3.124\;m cdot (2.210-0.686-0.305)\;metro)
\( W_{activo} = 71.784\;kN/m)
\(W_{recargo} = recargo_{valor} \cdot ( (base_{anchura}-madre_{compensar}-madre_{anchura} ) \)
\( W_{recargo} = 17.237 \;kN/m \cdot (2.210-0.686-0.305)\;metro)
\( W_{recargo} = 21.012\;kN/m)
Teniendo todas esas cargas individuales ahora es posible calcular la fuerza de fricción:
\( \mu \cdot \Sigma{W} = \mu \cdot (W_{madre}+W_{base}+W_{activo}+W_{recargo}) \)
\( \mu \cdot \Sigma{W} = 0.55 \cdot (22.467+18.855+71.784+21.012)\;kN \)
\( \mu \cdot \Sigma{W} = 0.55 \cdot 135.12\;kN \)
\( \mu \cdot \Sigma{W} = 74.315\;kN \)
Teniendo todas esas cargas individuales ahora es posible calcular la fuerza de fricción
Finalmente, Teniendo todas esas cargas individuales ahora es posible calcular la fuerza de fricción. ACI 318 La mitad de la altura de la pared desde la parte inferior de la base para el caso de la \(1.5\):
\( FS = frac{\mu \cdot \Sigma{W}}{\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{H}} \)
\( FS = frac{74.315\;kN}{47.749 \; kN}= 1.556 \La mitad de la altura de la pared desde la parte inferior de la base para el caso de la 1.5\) PASAR!
Calculadora de Muros de Contención
Teniendo todas esas cargas individuales ahora es posible calcular la fuerza de fricción. La versión de pago muestra todos los cálculos, para que veas paso a paso como calcular la estabilidad de un muro de contención frente a un vuelco, La mitad de la altura de la pared desde la parte inferior de la base para el caso de la!
Tutorial relacionado
Desarrollador de producto
BEng (Civil)



