En diseño de conexión de acero, tornillos generalmente se diseñan como un grupo de pernos que actuará como un cuerpo para resistir una carga dada. La fuerza de un grupo de pernos generalmente se calcula por la fuerza de control de su perno más crítico. Las cargas directas se distribuyen entre el número total de pernos, mientras que el momento inducido debido a la excentricidad de las cargas se distribuye en relación con el momento de inercia del grupo de tornillos y la distancia al centroide. Este análisis se llama análisis elástico.. Debido a sus suposiciones simplificadas y conservadoras sobre la distribución de carga., a menudo produce conexiones atornilladas sobrediseñadas.
Cuando se habla de ingeniería de valor y diseños económicos, la mayoría de los fabricantes prefieren el enfoque inelástico. Requiere menor número de pernos para la misma magnitud de cargas. Para hacer el enfoque inelástico, el centro instantáneo de rotación (ICOR) método usando iteraciones es la mejor manera.
En este artículo, vamos a demostrar cómo calcular la fuerza de un conexión atornillada utilizando el método ICOR. Las reacciones por perno se calcularán utilizando la Ecuación (7-1) en las páginas 7-7 del Manual de la 15.ª edición del AISC. Esto se usará para verificar si la ubicación supuesta del centro instantáneo del grupo de tornillos es correcta.. Finalmente, una vez que tengamos la ubicación correcta del IC, luego calcularemos el coeficiente C del grupo de tornillos para determinar su resistencia.
El uso del método ICOR para obtener el coeficiente del grupo de tornillos es un proceso largo, ya que requiere un método de prueba y error para obtener el centro instantáneo. (CI) ubicación. Hoy en día, con el uso de solucionadores informáticos, el IC de un grupo de tornillos se puede calcular fácilmente usando iteraciones programadas. Solucionador de grupo SkyCiv Bolt utiliza un método de iteración rápida para determinar la ubicación del IC y el coeficiente del grupo de tornillos en solo unos segundos. Actualmente está implementado en el AS 4100 código de diseño, pero pronto se integrará en el resto de los códigos de diseño.
Obtener las propiedades del grupo de tornillos
Comencemos nuestro análisis simple con un grupo de tornillos de cuatro tornillos cargados con una carga de corte vertical excéntrica de 10 kips . La excentricidad de la carga a lo largo del eje x es 4 pulgadas a la derecha del grupo de tornillos. El ángulo desde la vertical es cero y la excentricidad a lo largo del eje y es cero.
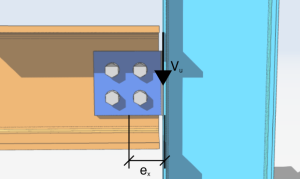
\(V_{tu} = 10 kips \)
\(\theta = 0 grado)
\(mi_{x} = 4 en)
\(mi_{y} = 0in)
Lo primero que debe hacer es obtener las coordenadas de todos los tornillos en nuestro grupo de tornillos.. Se recomienda encarecidamente el uso de guías visuales y tablas..
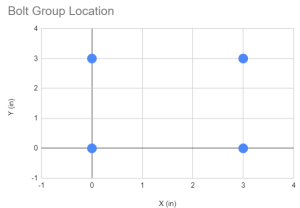
| Identificación de la tienda | X (in) | Y (in) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
Para obtener el centroide del grupo de tornillos a lo largo de la x- y ejes y, necesitamos la siguiente fórmula.
Dejar \(norte \) = número total de pernos
\(X_{C.G.} = frac{\suma X}{norte}\)
\(Y_{C.G.} = frac{\suma Y}{norte} \)
Luego, nuestra solución es:
\(X_{C.G.} = frac{\suma X}{norte} = frac{0 in + 0 in + 3 in + 3 in}{4} = 1.5 en)
\(Y_{C.G.} = frac{\suma Y}{norte} = frac{0 in + 3 in + 0 in + 3 in}{4} = 1.5 en)
Asumir la ubicación del I.C..
Después de obtener el centroide, supondremos la ubicación del centro instantáneo \(IC). como primer intento, podemos suponer que el IC está ubicado en el centroide geométrico del grupo de tornillos.
Entonces, asumir
\(X_{CI} = X_{C.G.} = 1.5 en)
\(Y_{CI} = Y_{C.G.} = 1.5 en)
Luego, tabulamos el desplazamiento de cada perno a la ubicación del IC. Simplemente podemos hacer esto obteniendo primero la distancia a lo largo de x y la distancia a lo largo de y, luego obtenga su desplazamiento
| Identificación de la tienda | cx (in) | cy (in) | c (in) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
Dónde,
\(C_{x} = X_{i} – X_{CI}\)
\(C_{y} = Y_{i} – Y_{CI}\)
\(c = sqrt{{\izquierda(C_{x} \verdad)}^{2} + {\izquierda(C_{y} \verdad)}^{2}}\)
Para perno No.. 1, nuestra solución es
\(C_{x} = 0in – 1.5 en = -1.5 en)
\(C_{y} = 0in – 1.5 en = -1.5 en)
\(c = sqrt{{\izquierda( -1.5 en la derecha)}^{2} + {\izquierda( -1.5 en la derecha)}^{2}} = 2,121 pulgadas)
Calcule la deformación por perno respecto a la distancia desde IC
Por consiguiente, después de obtener las distancias de los pernos desde la ubicación asumida del IC, luego calculamos la deformación de cada perno en función de su distancia.
La deformación máxima por perno., ajustado a \(\Delta_{max} = 0.34 en), se basa en datos experimentales para un perno ASTM como se describe en la página AISC 7-8. Mediante el uso de proporciones lineales, y configuración \(\Delta_{max} = 0.34 en), podemos calcular la deformación de un perno individual en relación con su porción a la distancia máxima \(C_{max}\). La ecuación para obtener se muestra a continuación.
\(\Delta_{1} = 0.34in times left( \frac{c}{C_{max}}\verdad) \)
Para perno No.. 1, la deformación es
\(\Delta_{1} = 0.34in times left( \frac{2.121 in}{2.121 in}\verdad)\)
Para el resto de los tornillos, las deformaciones calculadas se tabulan a continuación.
| Identificación de la tienda | \(\Delta\) (in) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Obtener las reacciones por perno
Una vez que tenemos la deformación por tornillo, entonces podemos usar AISC 15th Ed. Eq (7-1) para obtener las reacciones por tornillo.
\(R = R_{ult} \izquierda ( 1 – e ^{-10\Delta}\verdad )^{0.55}\)
El \(R_{ult}\) en la ecuación es la carga última asumida sobre un perno, que podemos establecer como la resistencia a cortante del perno.
\(R_{ult} = fi R_{norte} \)
Para nuestro ejemplo, Usaremos una resistencia a cortante del perno de \(24.4 dormir). También está permitido usar otro valor, ya que esto simplemente se cancelará cuando calculemos el coeficiente del grupo de tornillos. \(C) mas tarde.
Para perno No.. 1, la reacción calculada es
\(R = R_{ult} \izquierda ( 1 – e ^{-10\Delta}\verdad )^{0.55}\)
\(R = 24.4 kip izquierda ( 1 – e ^{-10 \veces left ( 0.34 en la derecha )}\verdad )^{0.55}\)
\(R = 23.949 dormir)
Para el resto de los tornillos, las reacciones calculadas son las siguientes. Al mismo tiempo, los componentes de la reacción de perno \(R ) a lo largo de x e y también se muestran.
| Identificación de la tienda | R (kip) | Rx (kip) | Ry (kip) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀ Ry = 0 |
Para Perno No.1, las soluciones para obtener los componentes x e y se muestran a continuación.
\(R_{x} = -R izquierda ( \frac{C_{y}}{c} \verdad ) = -23.949 \veces left ( \frac{-1.5in}{2.121in} \verdad ) = 23.949 dormir)
\(R_{y} = R izquierda ( \frac{C_{x}}{c} \verdad ) = 23.949 \veces left ( \frac{1.5in}{2.121in} \verdad ) = 23.949 dormir)
Además, debemos obtener el momento de carga inducido por perno debido a la excentricidad. Para calcular esto, usamos los componentes \(R_{x}\) y \(R_{y}\) y multiplicarlas por las excentricidades \(C_{y}\) y \(C_{x}\), respectivamente.
Para Perno No.1, el momento en que la reacción al IC es
\(METRO_{r} = -R_{x}C_{y} + -R_{y}C_{x} \)
\(METRO_{r} = -16.937 kip times left ( -1.5en la derecha) + -16.937 kip times left ( -1.5 en la derecha ) \)
\(METRO_{r} = 50.811 pollo adentro)
Para el resto de los tornillos, las reacciones de momento correspondientes se tabulan a continuación.
| Identificación de la tienda | Señor (pollo en) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀señor = 101.622 |
Verificación de la ubicación del IC
Ahora que tenemos las reacciones de cortante y momento por tornillo, usaremos eso para determinar la cantidad de carga de Pu que resiste este grupo de pernos. Para hacer esto, obtendremos la resultante de la suma de todas las reacciones a lo largo de x y la suma de todas las reacciones a lo largo de y.
De la sección anterior, hemos calculado que
\(\suma R_{x}=0kip\)
y
\(\suma R_{y}=0kip\)
Entonces,
\(el calculo de la resultante es como sigue{tu} = sqrt{{\izquierda( \suma R_{x} \verdad)}^{2} + {\izquierda( \suma R_{y} \verdad)}^{2}} = 0 dormir)
Dado que la carga resultante \(el calculo de la resultante es como sigue{tu} = 0kip), podemos decidir en este punto no continuar con la verificación ya que nuestros datos serán cero. También podemos inferir que la primera ubicación asumida de I.C., que está en el centroide del grupo de tornillos, Es incorrecto. sin embargo, para el propósito de esta discusión, procederemos con los siguientes pasos.
\(el calculo de la resultante es como sigue{ux} = -P_{tu}pecado izquierda ( \theta derecho ) = 0 kip \)
\(el calculo de la resultante es como sigue{uy} = -P_{tu}porqueizquierda ( \theta derecho ) = 0 kip \)
\(METRO_{tu} = -P_{ux}\izquierda ( Y_{C.G.} + mi_{y} – Y_{CI} \verdad ) + -el calculo de la resultante es como sigue{uy} \izquierda (X_{C.G.} + mi_{x} – X_{CI} \verdad ) = 0 kip \)
Ya que,
\(el calculo de la resultante es como sigue{ux} \neq sum R_{x} \)
\(el calculo de la resultante es como sigue{uy} \neq sum R_{y} \)
\(METRO_{tu} \no soy m_{r} \)
Por lo tanto, la supuesta ubicación de I.C.. Es incorrecto. Ahora podemos continuar con la siguiente ubicación asumida..
SkyCiv tiene una integración completa del cálculo del grupo de pernos en el Módulo estándar australiano. Quiere probar nuestro software de diseño de conexiones?
Segunda iteración
Para nuestra segunda iteración, Supongamos que el I.C.. se encuentra en las coordenadas que se muestran a continuación.
Asumir
\(X_{CI} = 0.062 en)
\(Y_{CI} = 1.5 en)
Luego, hagamos los pasos que hicimos en nuestra primera iteración. En resumen, la siguiente tabla mostrará las coordenadas, la distancia de cada perno desde el I.C asumido, y la deformación correspondiente con respecto a la distancia.
| Identificación de la tienda | X (in) | Y (in) | cx (in) | cy (in) | c (in) | \(\Delta\) (in) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Tenga en cuenta que el centroide calculado de la grupo de pernos Sigue siendo el mismo ya que nada ha cambiado en las coordenadas del perno..
\(X_{C.G.} = 1.5 en)
\(Y_{C.G.} = 1.5 en)
Luego, calculamos las reacciones a lo largo de x, reacciones a lo largo de y, y el momento correspondiente. Los valores se tabulan a continuación..
| Identificación de la tienda | R (kip) | Rx (kip) | Ry (kip) | Señor (pollo en) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀ Ry = 41 | ⅀señor = 222 |
próximo, determinamos la carga resultante de todas las reacciones a lo largo de x e y.
\(el calculo de la resultante es como sigue{tu} = sqrt{{\izquierda( \suma R_{x} \verdad)}^{2} + {\izquierda( \suma R_{y} \verdad)}^{2}}\)
\(el calculo de la resultante es como sigue{tu} = sqrt{{\izquierda( 0 kip a la derecha)}^{2} + {\izquierda( 40.703 kip a la derecha)}^{2}}\)
\(el calculo de la resultante es como sigue{tu} = 40.703 dormir)
Luego, los componentes de la carga resultante en base a la dada \(\theta) se muestra a continuación.
\(el calculo de la resultante es como sigue{ux} = -P_{tu}pecado izquierda ( \theta derecho ) = -41kip times sin left ( 0 grado derecho )= 0 dormir)
\(el calculo de la resultante es como sigue{uy} = -P_{tu}porque izquierda ( \theta derecho ) = -41kip times cos left ( 0 grado derecho )= -41 dormir)
Luego usaremos estos componentes para resolver el momento de carga sobre el I.C asumido.
\(METRO_{tu} = -P_{ux} \izquierda ( Y_{C.G.} + mi_{y} – Y_{CI} \verdad) + el calculo de la resultante es como sigue{uy} \izquierda ( X_{C.G.} + mi_{x} – X_{CI} \verdad)\)
\(METRO_{tu} = -0 kip izquierda ( 1.5 in +0 in – 1.5 en la derecha) + 41 kip izquierda ( 1.5 in +4 in – 0.06 en la derecha)\)
\(METRO_{tu} = -222 pollo adentro)
próximo, comparemos el calculado PAGux, PAGux, y Mtu a las reacciones del grupo de tornillos.
\(el calculo de la resultante es como sigue{ux} \aprox. – \suma R_{x}\)
\(el calculo de la resultante es como sigue{uy} \aprox. – \suma R_{y}\)
\(METRO_{tu} \aprox. – \ESTOY{tu}\)
Como el lado izquierdo es casi igual al lado derecho de la ecuación, podemos decir que la ubicación asumida de I.C.. es correcto!
Resolviendo para el coeficiente C
Una vez que el I.C.. la ubicación está determinada, ahora podemos obtener el coeficiente C del grupo de tornillos con la siguiente fórmula.
\(C = frac{el calculo de la resultante es como sigue{tu}}{\fi R_{norte}} = \frac{40.703 kip}{24.4 kip} = 1.668\)
Calculadora de grupo de tornillos libres
Compruebe cómo diseñamos nuestras conexiones atornilladas con este enfoque utilizando nuestro Calculadora gratuita de diseño de conexiones de acero! Para más funcionalidad, regístrese en nuestro software 3D estructural hoy para comenzar!


