Ejemplo de diseño de placa base usando EN 1993-1-8-2005, EN 1993-1-1-2005 y EN 1992-1-1-2004
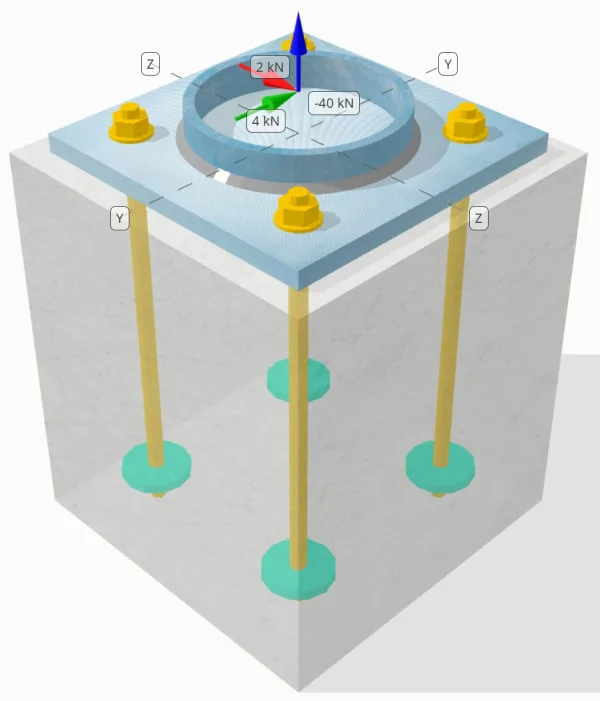
Declaración del problema
Determinar si la conexión de placa de columna a base diseñada es suficiente para un 50-carga de tensión kN, 4-kN Vy carga de corte, y 2-kN Vz carga de corte.
Datos dados
Columna:
Sección de columna: CHS193.7×10
Área de columna: 5770.0 mm²
Material de columna: S460
Plato base:
Dimensiones de placa base: 300mm x 300 mm
Espesor de la placa base: 18mm
Material de placa base: S235
Lechada:
Espesor de la lechada: 0 mm
Hormigón:
Dimensiones concretas: 350mm x 350 mm
Espesor de concreto: 400 mm
Material de hormigón: C35/45
Agrietado o sin crack: Agrietado
Ancla:
Diámetro de anclaje: 16 mm
Longitud de incrustación efectiva: 350 mm
Diámetro de placa incrustada: 70 mm
Espesor de la placa incrustada: 10 mm
Material de anclaje: 4.8
Soldaduras:
Tipo de soldadura: Filete
Tamaño de soldadura: 7mm
Clasificación de metal de relleno: E42
Aniquilar datos (de Calculadora de SkyCiv):
Modelo en la herramienta gratuita SkyCiv
Modele el diseño de la placa base anterior utilizando nuestra herramienta gratuita en línea hoy! No es necesario registrarse.
Notas
El propósito de este ejemplo de diseño es demostrar los cálculos paso a paso para verificaciones de capacidad que involucran cargas axiales y de corte simultáneas.. Algunas de las comprobaciones requeridas ya se han comentado en los ejemplos de diseño anteriores.. Consulte los enlaces proporcionados en cada sección..
Cálculos paso a paso
Cheque #1: Calcular la capacidad de soldadura
el completo carga de tracción es resistida por el toda la sección de soldadura, mientras que la componentes de carga de corte se distribuyen sólo a una porción de la longitud total de la soldadura. Esta porción se determina proyectando una 90°sector desde el centro de la columna hasta su circunferencia. Por lo tanto, solo la mitad de la circunferencia total está diseñado para resistir la carga de corte.
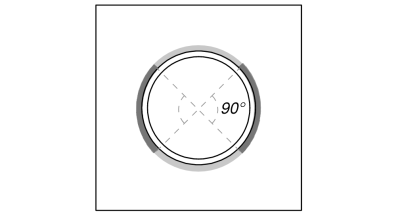
Primero calculamos el Longitud total de soldadura y el parte de la soldadura dentro de la proyección de 90°.
\(L_{soldar,lleno} = pid_{columna} = pi veces 193.7\ \texto{mm} = 608.53\ \texto{mm}\)
\(L_{soldar} = frac{\Pi D_{columna}}{2} = frac{\Pi Times 193.7\ \texto{mm}}{2} = 304.26\ \texto{mm}\)
próximo, calculamos el carga de corte resultante.
\(V_r = sqrt{(V_Y)^ 2 + (V_Z)^ 2} = sqrt{(4\ \texto{kN})^ 2 + (2\ \texto{kN})^ 2} = 4.4721\ \texto{kN}\)
Luego calculamos el normal y tensiones cortantes, teniendo en cuenta la distribución de carga supuesta.
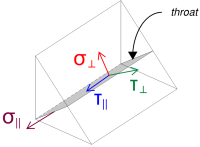
\( \sigma_{\perpetrador} = frac{N_X}{L_{soldar,lleno}\,a,sqrt{2}} = frac{40\ \texto{kN}}{608.53\ \texto{mm} \veces 4.95\ \texto{mm} \veces sqrt{2}} = 9.39\ \texto{MPa} \)
\( \tu_{\perpetrador} = frac{N_X}{L_{soldar,lleno}\,a,sqrt{2}} = frac{40\ \texto{kN}}{608.53\ \texto{mm} \veces 4.95\ \texto{mm} \veces sqrt{2}} = 9.39\ \texto{MPa} \)
\( \tu_{\paralelo} = frac{V_r}{L_{soldar}\,a} = frac{4.4721\ \texto{kN}}{304.26\ \texto{mm} \veces 4.95\ \texto{mm}} = 2.9693\ \texto{MPa} \)
Después, calculamos el tensiones combinadas usando EN 1993-1-8:2005 Eq. (4.1).
\(F_{w,Ed1} = sqrt{(\sigma_{\perpetrador})^ 2 + 3\grande((\tu_{\perpetrador})^ 2 + (\tu_{\paralelo})^2grande)}\)
\(F_{w,Ed1} = sqrt{(9.39\ \texto{MPa})^ 2 + 3\grande((9.39\ \texto{MPa})^ 2 + (2.9693\ \texto{MPa})^2grande)}\)
\(F_{w,Ed1} = 19.471\ \texto{MPa}\)
Al mismo tiempo, Determinamos el tensión en el metal base usando la misma ecuación.
\(F_{w,Ed2} =sigma_{\perpetrador} = 9.39\ \texto{MPa}\)
próximo, calculamos el capacidad de soldadura. Primero determinamos el resistencia máxima a la tracción (fu) del material más débil, y luego usar EN 1993-1-8:2005 Eq. (4.1) para obtener el resistencia de soldadura de filete y resistencia del metal base.
\(f_u = min!\izquierda(F_{tu,\texto{columna}},\ F_{tu,\texto{pb}},\ F_{tu,w}\verdad) = min!\izquierda(550\ \texto{MPa},\ 360\ \texto{MPa},\ 500\ \texto{MPa}\verdad) = 360\ \texto{MPa}\)
\(F_{w,Rd1} = frac{f_u}{\beta_w,(\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{M2,texto{soldar}})} = frac{360\ \texto{MPa}}{0.8 \veces (1.25)} = 360\ \texto{MPa}\)
\(F_{w,Td2} = frac{0.9\,f_u}{\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{M2,texto{soldar}}} = frac{0.9 \veces 360\ \texto{MPa}}{1.25} = 259.2\ \texto{MPa}\)
Ya que 19.471 MPa < 360 MPa, La capacidad de soldadura es suficiente.
Cheque #2: Calcule la capacidad de rendimiento de flexión de la placa base debido a la carga de tensión
Un ejemplo de diseño para la capacidad de fluencia a flexión de la placa base ya se analiza en el Ejemplo de diseño de placa base para tensión.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #3: Calcule la capacidad de ruptura de concreto en tensión
Un ejemplo de diseño para la capacidad del concreto en rotura debido a la carga de tensión ya se analiza en el Ejemplo de diseño de placa base para tensión.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #4: Calcular la capacidad de extracción de anclaje
En el Ejemplo de diseño de placa base para tensión ya se analiza un ejemplo de diseño para la capacidad de extracción del anclaje.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #5: Calcule la capacidad de reventón de la cara lateral en la dirección Y
Un ejemplo de diseño para la capacidad de explosión de la cara lateral en la dirección Y ya se analiza en el Ejemplo de diseño de placa base para tensión.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #6: Calcule la capacidad de reventón de la cara lateral en la dirección Z
Un ejemplo de diseño para la capacidad de explosión de la cara lateral en la dirección Z ya se analiza en el Ejemplo de diseño de placa base para tensión.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #7: Calcule la capacidad de carga de la placa base en los orificios de anclaje (Vy Shear)
Un ejemplo de diseño para la capacidad de carga de la placa base en los orificios de anclaje para corte Vy ya se analiza en el Ejemplo de diseño de placa base para compresión y corte.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #8: Calcule la capacidad de carga de la placa base en los orificios de anclaje (Cizalla de vz)
Un ejemplo de diseño para la capacidad de carga de la placa base en los orificios de anclaje para corte Vz ya se analiza en el Ejemplo de diseño de placa base para compresión y corte.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #9: Calcular la capacidad de rotura del hormigón. (Vy Shear)
Un ejemplo de diseño para la capacidad del concreto en caso de falla por rotura debido a corte Vy ya se analiza en el Ejemplo de diseño de placa base para corte.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #10: Calcular la capacidad de rotura del hormigón. (Cizalla de vz)
Un ejemplo de diseño para la capacidad del concreto en caso de falla por rotura debido a corte Vz ya se analiza en el Ejemplo de diseño de placa base para corte.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #11: Calcular la capacidad de extracción
Ya se analiza un ejemplo de diseño para la capacidad de extracción de concreto en el Ejemplo de diseño de placa base para corte.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #12: Calcular la capacidad de corte de la barra de anclaje
El efecto de la carga de tensión en la capacidad de la varilla de anclaje se considera en esta verificación si el La fuerza cortante actúa con un brazo de palanca.. sin embargo, en este ejemplo, los actos de corte sin brazo de palanca. Por lo tanto, La interacción entre las tensiones de corte y de tracción en la varilla de anclaje se evaluará por separado en el verificación de interacción.
Para calcular paso a paso la capacidad de corte sin brazo de palanca, por favor consulte este enlace.
El software SkyCiv Base Plate Design puede realizar todas las comprobaciones necesarias para determinar si la carga de corte actúa con o sin un brazo de palanca.. determinar más eficiente prueba la herramienta gratuita hoy.
Cheque #13: Calcular la verificación de interacción del acero del anclaje
Usamos EN 1992-4:2018 Tabla 7.3 Eq. (7.54) para evaluar el Interacción entre las tensiones de corte y tracción. en la barra de anclaje. Sustituyendo el esfuerzo de tracción y la capacidad, así como el esfuerzo de corte y la capacidad en la ecuación, el resultado valor de interacción es:
\(YO_{entero} = left(\frac{NORTE_{Ed}}{NORTE_{Rd,s}}\verdad)^ 2 + \izquierda(\frac{V_{Ed}}{V_{Rd,s}}\verdad)^2)
\(YO_{entero} = left(\frac{10\ \texto{kN}}{49.22\ \texto{kN}}\verdad)^ 2 + \izquierda(\frac{1.118\ \texto{kN}}{38.604\ \texto{kN}}\verdad)^2 = 0.042117\)
Ya que 0.042 < 1.0, la verificación de la interacción de falla del acero de la varilla de anclaje es suficiente.
Cheque #14: Calcular la verificación de interacción de falla concreta
Un adicional de verificación de interacción es necesario para fallas concretas bajo cargas simultáneas de corte y tracción. Para esto, usamos EN 1992-4:2018 Tabla 7.3 Eq. (7.55) y Eq. (7.56).
Aquí están las proporciones resultantes para todos controles de tracción.
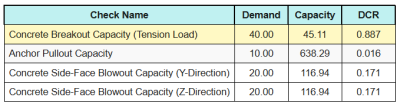
Aquí están las proporciones resultantes para todos controles de corte.
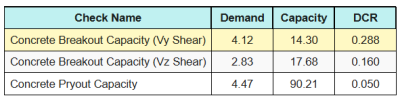
primero, comprobamos usando Eq. (7.55) y comparar el resultado con el límite máximo de interacción de 1.0.
\(YO_{\texto{caso1}} = left(\izquierda(\frac{NORTE_{Ed}}{NORTE_{Rd}}\verdad)^{1.5}\verdad) + \izquierda(\izquierda(\frac{V_{Ed}}{V_{Rd}}\verdad)^{1.5}\verdad)\)
\(YO_{\texto{caso1}} = left(\izquierda(\frac{40}{45.106}\verdad)^{1.5}\verdad) + \izquierda(\izquierda(\frac{4.1231}{14.296}\verdad)^{1.5}\verdad) = 0.99\)
próximo, comprobamos usando Eq. (7.56) y comparar el resultado con el límite máximo de interacción de 1.2.
\(YO_{\texto{Caso2}} = frac{NORTE_{Ed}}{NORTE_{Rd}} + \frac{V_{Ed}}{V_{Rd}} = frac{40}{45.106} + \frac{4.1231}{14.296} = 1.1752\)
Ya que 0.99 < 1.0 y 1.175 < 1.2, la verificación de interacción de falla concreta es suficiente.
Resumen de diseño
El Software de diseño de placa base de SkyCiv puede generar automáticamente un informe de cálculo paso a paso para este ejemplo de diseño. También proporciona un resumen de los controles realizados y sus proporciones resultantes, Hacer que la información sea fácil de entender de un vistazo. A continuación se muestra una tabla de resumen de muestra, que se incluye en el informe.
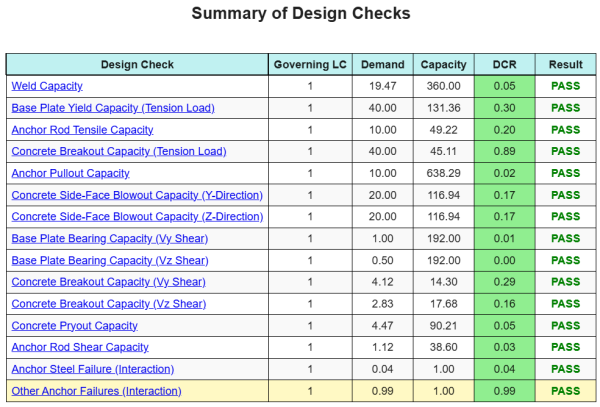
Informe de muestra de SkyCiv
Vea el nivel de detalle y claridad que puede esperar de un informe de diseño de placa base SkyCiv. El informe incluye todas las comprobaciones de diseño clave., ecuaciones, y resultados presentados en un formato claro y fácil de leer. Cumple totalmente con los estándares de diseño.. Haga clic a continuación para ver un informe de muestra generado con la calculadora de placa base SkyCiv.
(Informe de muestra que se agregará pronto)
Comprar software de placa base
Compre la versión completa del módulo de diseño de la placa base por sí solo sin ningún otro módulo SkyCiv. Esto le da un conjunto completo de resultados para el diseño de placa base, incluyendo informes detallados y más funcionalidad.


