El centroide o centro de masa de las secciones de vigas es útil para el análisis de vigas cuando se requiere el momento de inercia para cálculos como corte/Esfuerzo de flexión y deflexión. Este artículo lo guía a través de un proceso simple de cómo calcular el centroide y lo presenta a SkyCiv Free Centroid Calculator.
Cómo encontrar el centroide
En primer lugar, necesitas saber cómo encontrar el centroide. Las secciones de viga generalmente están formadas por una o más formas. Entonces, para encontrar el centroide de un área de sección de viga completa, primero debe dividirse en segmentos apropiados. Después de este, el área y el centroide de cada segmento individual deben considerarse para encontrar el centroide de toda la sección.
Considere la sección de viga en I que se muestra a continuación. Para calcular el centroide vertical (en la dirección y) se puede dividir en 3 segmentos como se ilustra:
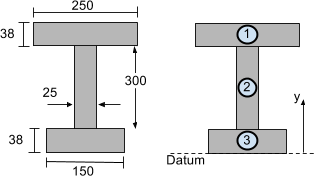
Ahora simplemente necesitamos usar la ecuación del centroide para encontrar la vertical. (y) centroide de una forma de múltiples segmentos:

Tomaremos el dato o la línea de referencia desde la parte inferior de la sección de la viga. Ahora busquemos Ai y yi para cada segmento de la sección del haz I que se muestra arriba, de modo que se pueda encontrar el centroide vertical o y.
[math]
\texto{Segmento 1:}\\
\empezar{alinear}
{A}_ _{1} &= 250 times38 = 9500 {\texto{ mm}}^{2}\\
{y}_ _{1} &= 38 + 300 + \tfrac{38}{2} = 357 \texto{ mm}\\\\
\final{alinear}
[math]
[math]
\texto{Segmento 2:}\\
\empezar{alinear}
{A}_ _{2} &= 300 times25 = 7500 {\texto{ mm}}^{2}\\
{y}_ _{2} &= 38 + \tfrac{300}{2} = 188 \texto{ mm}\\\\
\final{alinear}
[math]
[math]
\texto{Segmento 3:}\\
\empezar{alinear}
{A}_ _{3} &= 38 times150 = 5700 {\texto{ mm}}^{2}\\
{y}_ _{3} &= tfrac{38}{2} = 19 texto{ mm}\\\\
\final{alinear}
[math]

En el caso de que la sección transversal esté compuesta por dos materiales o un material compuesto, entonces uno de los materiales tendrá que multiplicarse por la relación modular de modo que toda la sección de la ecuación se vuelva uniforme.
[math]
n = frac{MI_{1}}{MI_{2}}
[math]
Típicamente, E1 es el módulo de elasticidad del material no predominante, y E2 es el módulo de elasticidad del material predominante, aunque cualquier orden preferido no afectará la solución del centroide. Ajuste para el segundo material, la ecuación del centroide se convierte en la siguiente.
[math]
\bar{y}= frac{\suma{A}_ _{i}{y}_ _{i}+\suma {norte}{A}_ _{i}{y}_ _{i}}{\suma{A}_ _{i}+\suma {norte}{A}_ _{i}}
[math]
Encuentra el centroide del haz con SkyCiv
Encontrar el centroide de la viga es importante, pero calcularlos manualmente puede llevar mucho tiempo.. SkyCiv ofrece una Calculadora de centroides gratis que automatiza este proceso para usted, ayudándote a encontrar la vertical (y) y horizontal (x) centroides de secciones de vigas de forma fácil y precisa!
Esta herramienta es una versión gratuita de SkyCiv Section Builder, un completo software de análisis de secciones en línea para analizar geometrías., de flexión, propiedades de corte y sección de torsión, así como FEA y diseño de hormigón armado. Con esta herramienta, puedes crear secciones personalizadas usando plantillas predefinidas o definir tus propias formas con puntos, líneas, o importaciones DXF desde CAD.
Para explorar todas las funciones SkyCiv Section Builder y experimente la facilidad de modelar y analizar su sección, Registrese gratis hoy!
Recursos Relacionados


