Cómo calcular una viga indeterminada – Método Integral Doble

Indeterminado vigas puede ser un desafío debido a los pasos adicionales necesarios para resolver las reacciones. Recuerde que las estructuras indeterminadas tienen lo que se llama un grado de indeterminación.. Para resolver la estructura, se deben introducir condiciones de contorno. Por consiguiente, cuanto mayor es el grado de indeterminación, Cuantas más condiciones de contorno tengan que ser identificadas. Pero antes de que podamos resolver un rayo indeterminado, primero necesitamos identificar si el haz es estáticamente indeterminado. Como las vigas son estructuras unidimensionales, usar la ecuación para determinar estructuras estáticamente indeterminadas externamente es suficiente.

[math]
yo_{mi}= R- izquierda ( 3+mi_{c} \verdad )
[math]

Dónde:

• i_mi = Grado de indeterminación
• R = número total de reacciones
• mi_c = Condiciones externas (ej. bisagra interna)

Típicamente, sin embargo, sin necesidad de resolver el grado de indeterminación, cualquier otra cosa que no sean luces simples o vigas en voladizo son estáticamente indeterminadas, asumiendo que tales vigas no vienen con bisagras internas.

Hay muchas formas de abordar la resolución de vigas indeterminadas.. Aunque por simplicidad y similitud con SkyCiv Beam los cálculos manuales, discutiremos el método de doble integración.

Doble integración

La doble integración es quizás el más simple de todos los métodos para el análisis de vigas.. El concepto de este método es bastante sencillo en comparación con otros métodos, ya que se basa principalmente en una comprensión básica del cálculo integral., de ahí el nombre. Se adapta un poco de cálculo integral de la relación de la curvatura de la viga al momento que se muestra a continuación.

[math]
\frac{1}{\rho}= frac{M}{EI}
[math]

Tenga en cuenta que 1 / ρ es la curvatura de la viga y que ρ es el radio de la curva. Fundamentalmente, la definición de curvatura es la tasa de cambio de la tangente con respecto a la longitud del arco. Como el momento es una función de la carga con respecto a la longitud del miembro, La integración de la curvatura con respecto a la longitud del miembro producirá la pendiente de la viga. De igual forma, La integración de la pendiente con respecto a la longitud del miembro dará lugar a la desviación del haz. Como las cargas estructurales típicas son de naturaleza algebraica, La integración de estas expresiones es tan simple como usar la fórmula de poder general.

[math]
\int f left ( x right )^{norte}dx = frac{f left ( x right )^{n + 1}}{n + 1}+C
[math]

Quizás la mejor manera de entender el concepto es proporcionando un ejemplo de una viga con lo siguiente dado.

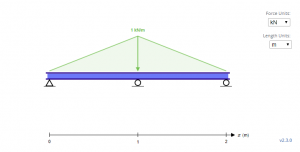
La viga de muestra de arriba es una viga indeterminada con cargas triangulares.. Con el soportes, A_y, B_y y C_y Por el primero, segundo, y terceros soportes respectivamente, El primer paso para resolver estas incógnitas es comenzar con las ecuaciones de equilibrio..

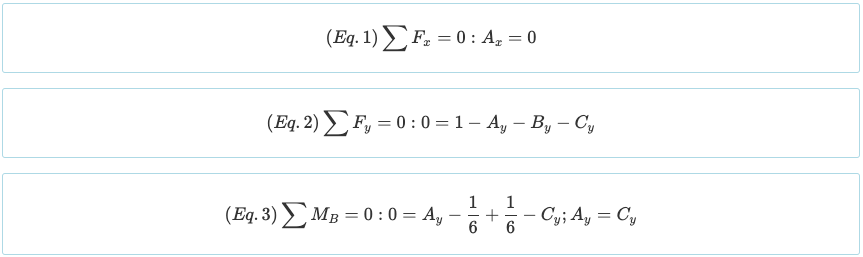
Tenga en cuenta que el haz tiene un grado de indeterminación estática de 1°. Como hay cuatro incógnitas (A_x, A_y, B_y, y C_y) y hay tres ecuaciones hasta ahora de las ecuaciones de equilibrio anteriores, es necesario crear una ecuación más a partir de las condiciones de contorno. Recuerde que el momento generado por una carga puntual y una carga triangular son los siguientes.

Carga puntual:

[math]
M = F veces x; M = Fx
[math]

Carga triangular:

[math]
M = frac{w_{0}\veces x}{2}\veces left ( \frac{x}{3} \verdad ); M = frac{w_{0}x ^{2}}{6}
[math]

Mediante el uso del método de doble integración, estas nuevas ecuaciones se hacen y se muestran a continuación.

Nota: Las ecuaciones anteriores se escriben como funciones de Macaulay donde una expresión es igual a cero cuando x < L. En este caso, L = 1.

En las ecuaciones anteriores, note que el cuarto término agregado parece salir de la nada. De hecho, la dirección de la carga es opuesta a la dirección de la gravedad. Esto se debe al hecho de que las ecuaciones para cargas triangulares solo funcionan cuando la carga asciende a medida que aumenta la longitud. Esto no es un gran problema para las ecuaciones para repartido y cargas puntuales por su simetría. En efecto, la carga equivalente para la viga de arriba se parece a la viga de abajo, así las ecuaciones se basan en ello.

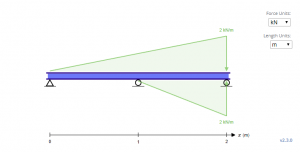
Para resolver por C₁ y C₂, las condiciones de contorno tienen que ser determinadas. En la viga de arriba, se puede observar que existen tres de estas condiciones límite en x = 0, x = 1, y x = 2, donde la desviación y es cero en las tres ubicaciones.

Condición límite 1

[math]
x = 0, y=0; C_{2}= 0
[math]

Condición límite 2

[math]
x = 0, y=0; C_{1}= frac{1}{120}-\frac{UNA_{y}}{6}
[math]

Después de determinar los valores de cada constante, Ahora se puede obtener la última ecuación utilizando la última condición de contorno.

Condición límite 3

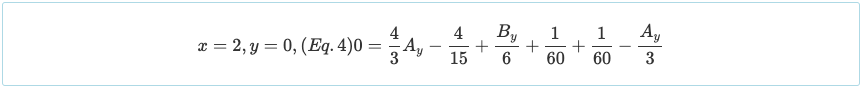
Tenga en cuenta que la condición límite de θ = 0 en x = 1 puede ser usado, aunque es aplicable solo para la reacción media de un haz continuo simétrico con carga simétrica.

Como se han determinado las cuatro ecuaciones, ahora pueden resolverse simultáneamente. Resolver estas ecuaciones producirá las siguientes reacciones.

Con las reacciones determinadas, los valores de las reacciones pueden sustituirse de nuevo a la ecuación de momento. Esto nos permitirá determinar el valor del momento en cualquier parte del sistema de haces..

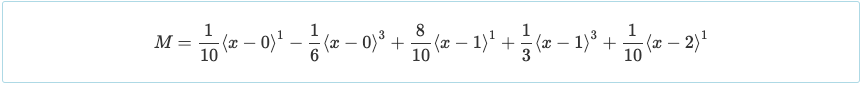
Otra conveniencia de Double Integration es que la ecuación de momento se presenta de una manera que se puede usar para resolver el corte con la relación que se muestra a continuación.

[math]
V = frac{dM}{dx}
[math]

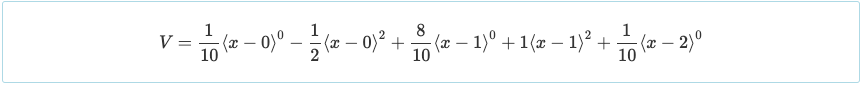
De nuevo, utilizando solo una comprensión básica del cálculo diferencial, equiparar la derivada de una función a cero produce el máximo o mínimo de esa función. Así, equiparando V = 0 dará como resultado un momento positivo máximo en x = 0.447 y x = 1.553 de M = 0.030

Por supuesto, todo esto se puede verificar con SkyCiv Beam.

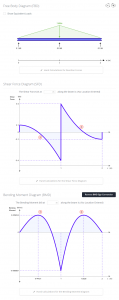
Software SkyCiv Beam

Software de análisis de vigas de SkyCiv permite a los usuarios analizar estructuras de vigas con facilidad y precisión. Puede obtener un análisis de su miembro de viga, entre ellos reacciones, fuerza de cortante, momento flector, deflexión, y tensiones en cuestión de segundos.

Si quiere probarlo primero, Calculadora gratis de vigas es una gran manera de empezar, o simplemente regístrese gratis hoy!