Tabla de Contenidos
- Tipos de soportes y sus reacciones
- Una guía paso a paso para determinar las reacciones de los soportes en vigas
- Software SkyCiv Beam
Tipos de soportes y sus reacciones
primero, También es importante comprender los diferentes tipos de soportes y qué reacciones producen en su modelo de análisis.. A continuación se muestra una breve tabla de resumen de los diferentes tipos de apoyo y sus reacciones.:
| Tipo de apoyo | Traducción | Rotación | Notas |
|---|---|---|---|
Soporte fijo |
Fijo en todas las direcciones Reacciones en X,Y,Z |
Fijo en todas las direcciones Reacciones en X,Y,Z |
FFFFFF – Reacciones en todos los grados de libertad. |
Soporte de rodillos horizontales |
Fijo en Y Reacciones en dirección Y solamente |
Liberado en todas las direcciones Sin reacciones rotacionales |
RFFRRR – Las reacciones son solo en la dirección Y. |
Soporte articulado o articulación |
Fijo en X,Y,Z Reacciones en X,Y,Z |
Liberado en todas las direcciones Sin reacciones rotacionales |
FFFRRR – Reacciones en toda la traducción., ninguno en rotación |
Soporte en voladizo |
Fijo en todas las direcciones Reacciones en X,Y,Z |
Fijo en todas las direcciones Reacciones en X,Y,Z |
Igual que el fijo |
Una guía paso a paso para determinar las reacciones de los soportes en vigas:
La determinación de las reacciones en los soportes es siempre el primer paso en el análisis de la estructura de una viga., y generalmente es el más fácil. Implica calcular tanto la fórmula de la fuerza de reacción como los momentos de reacción en los apoyos. (soportes A y B en el siguiente ejemplo) debido a las fuerzas que actúan sobre la viga. La fórmula de la fuerza de reacción se utiliza para encontrar las fuerzas ejercidas en los apoyos debido a las cargas que actúan sobre la viga.. Necesitará saber esto para avanzar y calcular diagramas de momento flector (DMO) y diagramas de fuerza de corte (SFD); una parte importante de sus cursos de estática y estructurales de la universidad. SkyCiv ofrece una poderosa Calculadora de reacción gratuita que le permite modelar cualquier viga y mostrar estos cálculos manuales por usted, pero también es un concepto importante para entender.
Videotutorial: Determine las reacciones en los apoyos.
Al resolver un problema como este, primero debemos recordar que la viga es estática; lo que significa que no se mueve. De física simple, esto significa que la suma de las fuerzas en la dirección y es igual a cero (Es decir. las fuerzas descendentes totales son iguales a las fuerzas ascendentes totales). Una segunda fórmula para recordar es que la suma de los momentos sobre cualquier punto dado es igual a cero. Esto se debe a que la viga es estática y, por lo tanto, no gira..
Para determinar las reacciones en los soportes., sigue estos sencillos pasos:
1. Suma de Momentos (ΣM = 0)
Todo lo que necesitamos saber sobre los momentos en esta etapa es que son iguales a la fuerza multiplicada por la distancia desde un punto. (Es decir. la fuerza x distancia desde un punto). Considere un ejemplo simple de una viga de 4 m con un soporte articulado en A y soporte de rodillo en B. El diagrama de cuerpo libre se muestra a continuación donde Ay y By son las reacciones verticales en los soportes: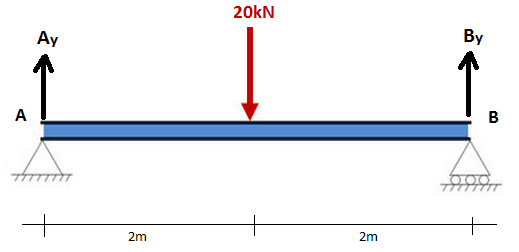
Primero queremos considerar la suma de momentos con respecto al punto B y dejar que sea igual a cero. Hemos elegido el punto B para demostrar que esto se puede hacer en cualquier extremo de la viga (siempre que sea soportado por un soporte articulado). sin embargo, podrías trabajar con la misma facilidad desde el punto A. Entonces, ahora sumamos los momentos sobre el punto B y dejamos que la suma sea igual 0:
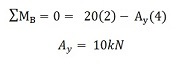
NOTA: La convención de signos que hemos elegido es que los momentos en sentido antihorario son positivos y los momentos en sentido horario son negativos. Esta es la convención de signos más común, pero depende de usted. SIEMPRE debe usar la misma convención de signos en todo el problema. Utilice siempre la misma convención de signos desde el principio. Ahora tenemos nuestra primera ecuación. Necesitamos resolver otra ecuación para encontrar By (la fuerza de reacción vertical en el soporte B).
2. Suma de fuerzas horizontales (ΣFy = 0)
Sume las fuerzas en el eje y (vertical) y deje que la suma sea igual a cero. Recuerde incluir todas las fuerzas, incluidas las reacciones y las cargas normales, como las cargas puntuales.. Entonces, si sumamos las fuerzas en la dirección y para el ejemplo anterior, obtenemos la siguiente ecuación:
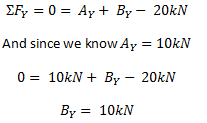
NOTA: Una vez más nos apegamos a la convención de signos que consiste en tomar fuerzas hacia arriba (nuestras reacciones) como fuerzas positivas y descendentes (la carga puntual) como negativa. Recuerde que la convención de signos depende de usted, pero SIEMPRE debe usar la misma convención de signos durante todo el problema..
Así que ahí lo tenemos, hemos usado las dos ecuaciones anteriores (suma de momentos es igual a cero y suma de fuerzas verticales es igual a cero) el calculo de la reacción en el soporte A es 10 kN y la reacción en el soporte B 10kN. Esto tiene sentido ya que la carga puntual está justo en el medio de la viga, lo que significa que ambos soportes deberían tener las mismas fuerzas verticales (Es decir. es simétrico).
Al determinar las fuerzas que actúan sobre la viga., Se utilizan tanto la suma de fuerzas como la suma de momentos.. La fórmula de la fuerza de reacción ayuda a calcular las fuerzas verticales y horizontales., mientras que sumar los momentos de reacción le permite garantizar que la viga permanezca en equilibrio estático.
En resumen, aquí están completos los cálculos manuales producidos por SkyCiv Beam:
Software SkyCiv Beam
A través de este artículo, Has aprendido a encontrar la fuerza de reacción.. Software de análisis de vigas de SkyCiv permite a los usuarios analizar estructuras de vigas con facilidad y precisión. Puede obtener un análisis de su miembro de viga, incluyendo reacciones, fuerza de cortante, momento flector, deflexión, tensiones, y vigas indeterminadas en cuestión de segundos.
Si quiere probarlo primero, Calculadora gratis de vigas es una gran manera de empezar, o simplemente regístrese gratis hoy!