Un ejemplo completamente trabajado de Ground-mounted Cálculo de carga de viento y presión de nieve del panel solar usando ASCE 7-16
[object Window], una de las industrias de rápido crecimiento como solución a este problema es el uso de la energía solar. Además, una de las industrias de rápido crecimiento como solución a este problema es el uso de la energía solar. En efecto, una de las industrias de rápido crecimiento como solución a este problema es el uso de la energía solar. La necesidad de calcular la carga del viento en los paneles solares, así como las presiones de la nieve, es fundamental para que estos alcancen la durabilidad.. En este artículo, discutiremos cómo calcular las cargas de nieve y viento en paneles solares montados en el suelo usando ASCE 7-16.
SkyCiv automatiza los cálculos de la velocidad del viento con unos pocos parámetros. Pruebe nuestro Calculadora de carga de viento del panel solar
Datos de estructura
En este ejemplo, utilizaremos los siguientes datos:
Tabla 1. Datos de construcción necesarios para nuestro cálculo de carga de viento y nieve.
| Ubicación | 395 Rocky Point Road, Cordova, Memphis, Tennesse |
| Ocupación | Miscelánea – Solar Panel |
| Terreno | Campo plano |
| Las dimensiones del panel solar | 16.25 ft |
| Las dimensiones del panel solar | 13.33 ft |
| Las dimensiones del panel solar | 8.33 ft |
| Las dimensiones del panel solar | 30° |
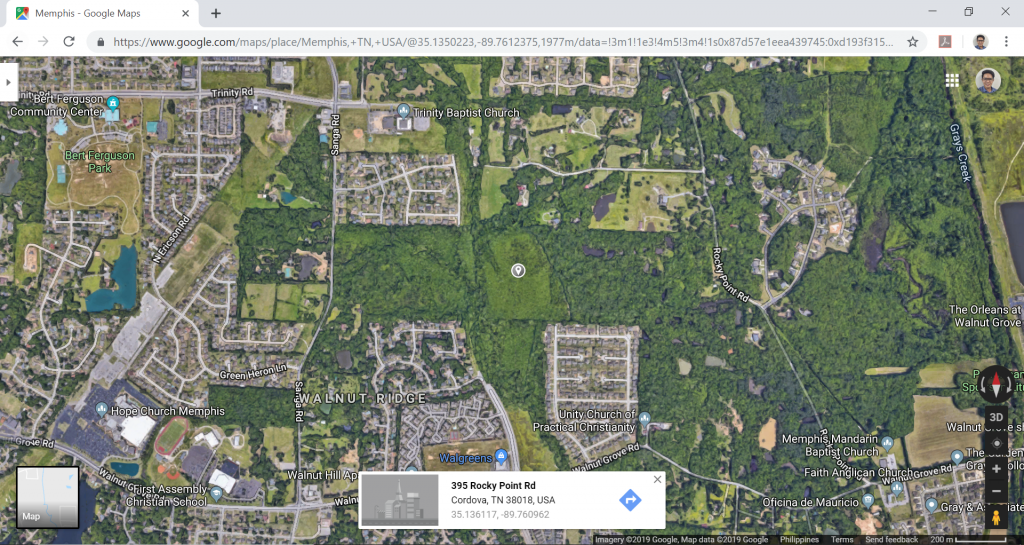
Figura 1. Ubicación del sitio (de Google Maps).
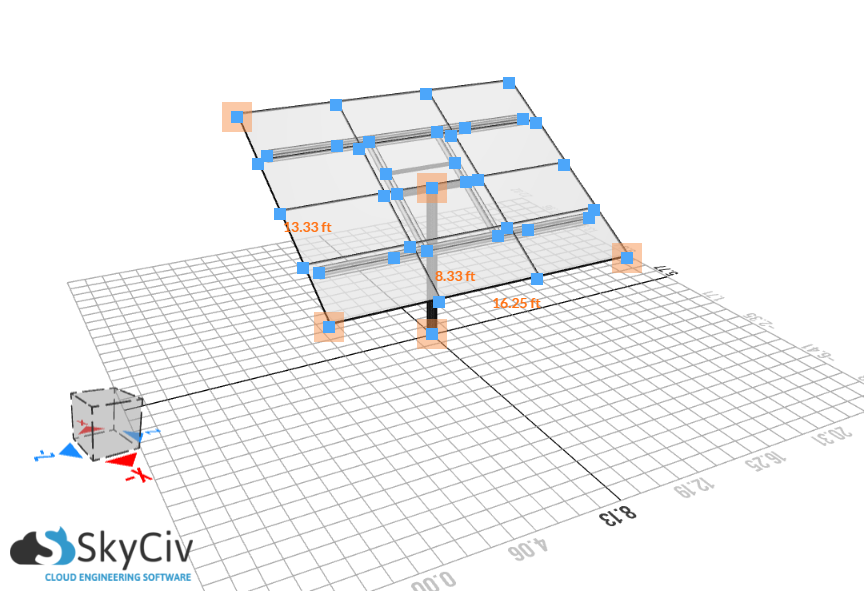
Figura 2. Las dimensiones del panel solar.
Carga de viento
En el cálculo de la carga de viento en los paneles solares, estaremos usando el ASCE 7-16 Capítulo 27 – Carga de viento – Consideraremos el panel solar montado en el suelo como un edificio de monopendiente abierto cuando el ángulo de inclinación sea menor o igual a 45° y como un signo sólido para un ángulo de inclinación mayor a 45°.. Consideraremos el panel solar montado en el suelo como un edificio abierto con techo monopendiente cuando el ángulo de inclinación sea menor o igual a 45° y como un signo sólido para un ángulo de inclinación mayor a 45°..
La fórmula para determinar las presiones de viento de diseño es la siguiente:
Para ángulo de inclinación ≤ 45° (considerado como un edificio abierto con techo de una sola pendiente):
\(p = {q}_{h}G{C}_{N}\) (1)
Para ángulo de inclinación > 45° (considerado como signo sólido):
\(p = {q}_{h}G{C}_{f}\) (2)
Dónde:
\(G\) = Factor de efecto de ráfaga
\({C}_{N}\) = coeficiente de fuerza neta para techo monopendiente abierto
\({C}_{f}\) = coeficiente de fuerza neta para señales sólidas
\({q}_{h}\) = presión de velocidad a la altura de referencia, \(h\), en psf, dada por la fórmula:
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\) (3)
\({K}_{z}\) = coeficiente de presión de velocidad
\({K}_{zt}\)= factor topográfico
\({K}_{d}\) = factor de direccionalidad del viento
\({K}_{e}\) = factor de elevación del suelo
\(V \) = velocidad básica del viento en mph
Tenga en cuenta que para el ángulo de inclinación > 45°, las dimensiones a utilizar son la proyección vertical del panel solar y luego usamos la fórmula para coeficientes de fuerza neta para señales sólidas. Vamos a profundizar en los detalles de cada parámetro a continuación.
Categoría de Riesgo
El primer paso es determinar la categoría de riesgo del panel solar en función del uso o la ocupación.. De la tabla 1.5-1 de ASCE 7-16, podemos clasificar el panel solar montado en el suelo en este ejemplo en la Categoría de riesgo I.
Velocidad Básica del Viento, \(V\)
La ASCE 7-16 proporciona un mapa de viento donde se puede obtener la velocidad básica del viento de una ubicación a partir de las Figuras 26.5-1A a 1C. De la figura 26.5-1A, Cordova, Memphis, Tennessee está cerca del punto rojo en la Figura 3 a continuación, y a partir de ahí, la velocidad básica del viento, \(V\), es 100 mph. Tenga en cuenta que el valor básico de la velocidad del viento se interpola a partir de los contornos de viento más cercanos.
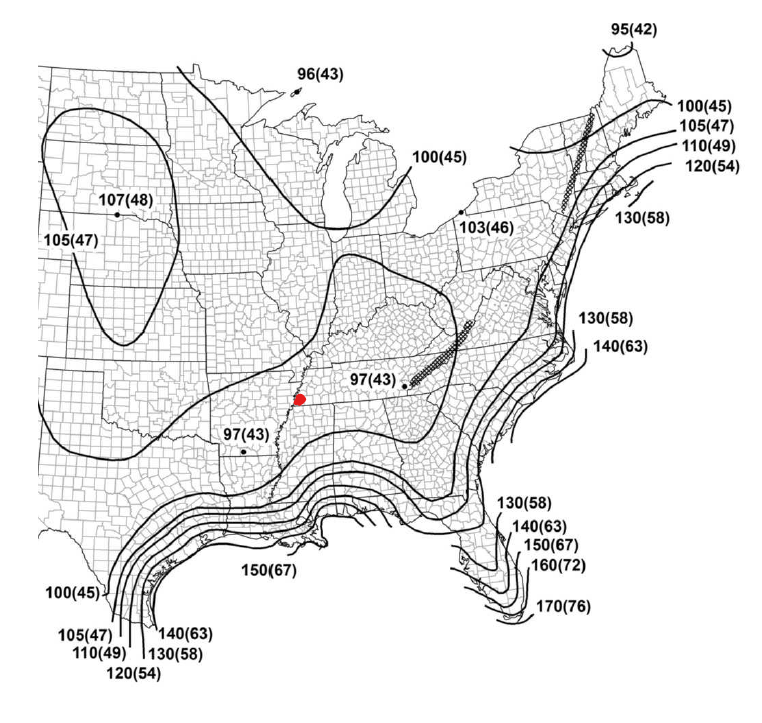
Figura 3. Mapa básico de velocidad del viento de la Figura 26.5-1A de ASCE 7-16 (Categoría de riesgo I) con punto rojo para indicar la ubicación de nuestro panel solar.
SkyCiv automatiza los cálculos de la velocidad del viento con unos pocos parámetros. Pruebe nuestro Calculadora de carga de viento del panel solar
Categoría de Exposición
Dependiendo de la dirección del viento que se analice, la categoría de exposición del panel solar se determinará a partir del sector de 45° contra el viento según la Sección 26.7 de ASCE 7-16. Además, La sección C26.7 proporciona fotografías aéreas que muestran ejemplos de exposiciones B, C, y D en las Figuras C26.7-5 a C26.7-7.
En este ejemplo, solo usaremos el viento que viene de la dirección Sur. Por lo tanto, basado en los ejemplos de fotografías aéreas, podemos clasificar el terreno a barlovento a Exposición C con base en la Figura C26.7-6(b) o “Terreno abierto con obstrucciones dispersas que tienen alturas generalmente menores a 30 ft (9.1 m)” como se muestra en la figura 4 a continuación. Usaremos la categoría de exposición para calcular el coeficiente de presión de velocidad \({K}_{z}\)durar> y/o factor topográfico \({K}_{zt}\) si es necesario.
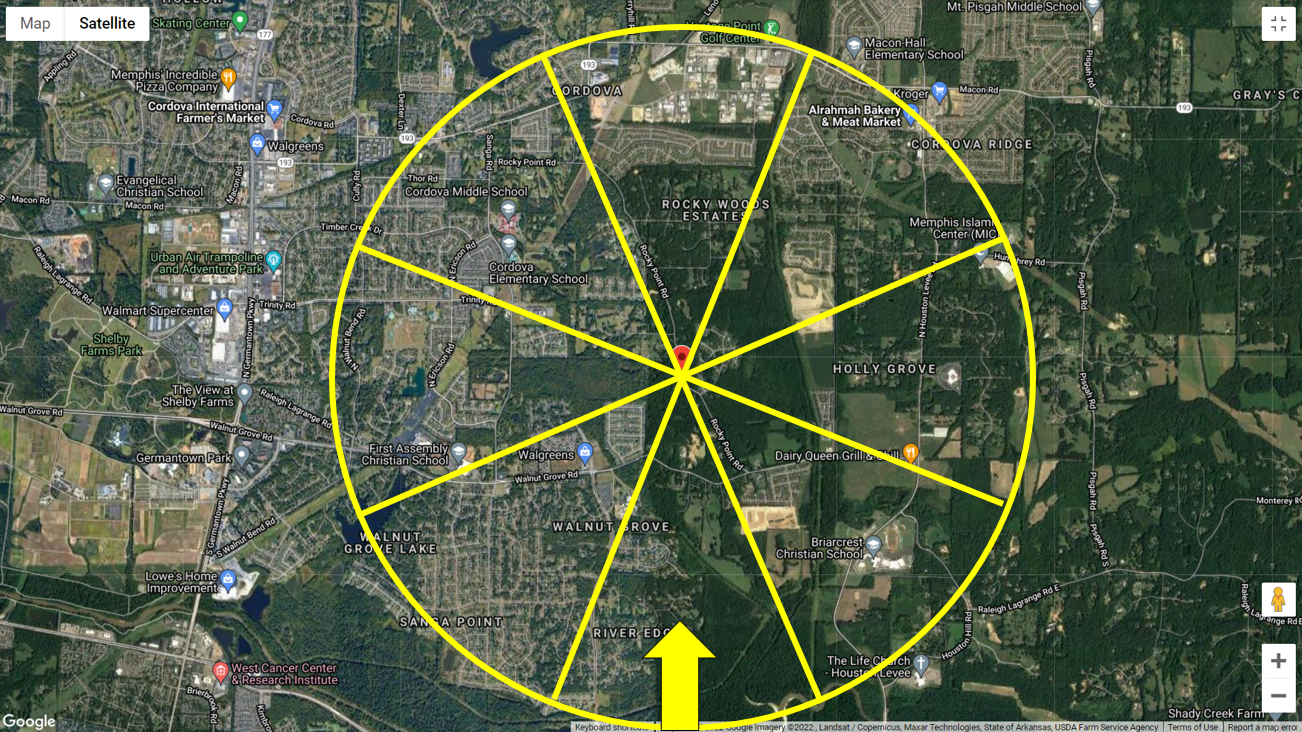
Figura 4. Fotografía aérea del terreno con viento proveniente del Sur.
Factor de Direccionalidad del Viento, \( {K}_{d} \)
El factor de direccionalidad del viento, \({K}_{d} \), para el panel solar es igual a 0.85 ya que el panel solar se puede considerar como MWFRS (asce7) cuando el ángulo de inclinación es menor o igual a 45° y como un signo sólido para un ángulo de inclinación mayor a 45° basado en la Tabla 26.6-1 de ASCE 7-16.
Factor de elevación del suelo, \( {K}_{e} \)
El factor de elevación del suelo, \({K}_{e} \), se puede calcular utilizando la Tabla 26.9-1 de ASCE 7-16. En este ejemplo, ya que la elevación del sitio es igual a 350.48 ft, \({K}_{e} \) se puede calcular usando la fórmula:
\( {K}_{e} = {e}^{-0.0000362{z}_{g}} \) (4)
\( {K}_{e} = {e}^{-0.0000362(350.48)} = 0.987\)
\( {K}_{e} = 0.987 \)
Usando la ecuación (4), \({K}_{e} \) es igual a 0.987.
Factor Topográfico, \( {K}_{zt} \)
Los parámetros para calcular el factor topográfico, \({K}_{zt}\), se detallan en la figura 26.8-1 de ASCE 7-16. Para determinar si se requieren más cálculos del factor topográfico, necesitamos verificarlo usando la Sección 26.8.1. Si el sitio no cumple con todas las condiciones enumeradas, el factor topográfico se puede tomar como 1.0. Desde la elevación del suelo generada a partir de las elevaciones de Google, podemos suponer que el terreno es plano, por lo tanto, \({K}_{zt}\) se puede suponer que es 1.0 para el viento que viene del Sur.
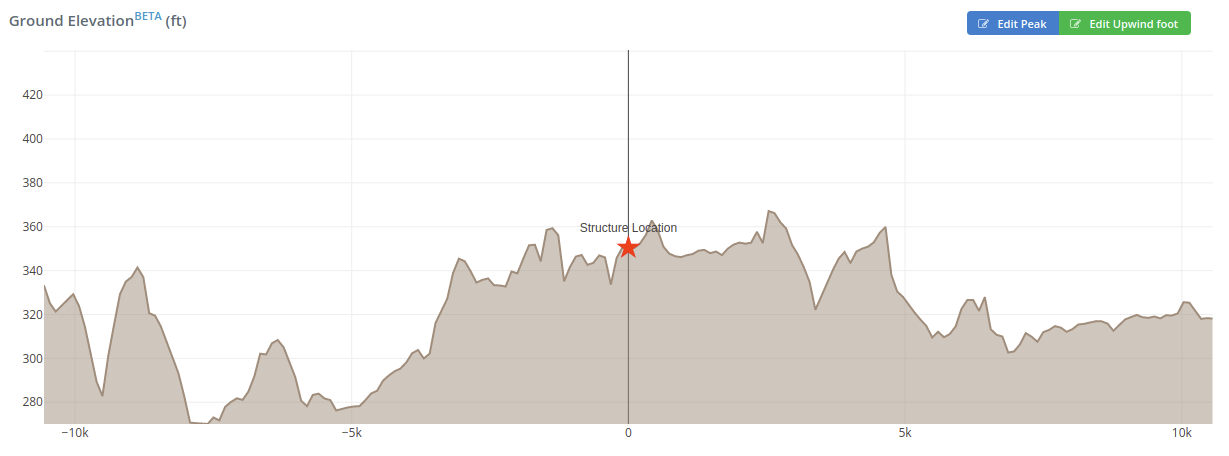
Figura 5. Perfil de elevación del sitio en la dirección del viento S-N.
Coeficiente de Presión de Velocidad, \({K}_{z}\)
El coeficiente de presión de velocidad, \({K}_{z}\), se puede calcular utilizando la Tabla 26.10-1 de ASCE 7-16. Este parámetro depende de la altura sobre el nivel del suelo en el punto donde se considera la presión del viento, y de la categoría de exposición. Además, los valores mostrados en la tabla se basan en la siguiente fórmula:
Para 15ft < \({z}\) < \({z}_{g}\): \({K}_{z} = 2.01(z/{z}_{g})^{2/α}\) (5)
Por \({z}\) < 15ft: \({K}_{z} = 2.01(15/{z}_{g})^{2/α}\) (6)
Dónde:
Tabla 3. Valores de α y \({z}_{g}\) según la tabla 26.11-1 de ASCE 7-16.
| Exposición | una | \({z}_{g}\) (ft) |
|---|---|---|
| B | 7 | 1200 |
| C | 9.5 | 900 |
| re | 11.5 | 700 |
En este ejemplo, consideraremos la elevación de la altura de montaje solar.
\({K}_{z} = 2.01((15)/(900))^{2/(9.5)} = 0.85 \)
\({K}_{z} = 0.85 \)
Presión de Velocidad
A partir de la Ecuación (3), podemos resolver la presión de velocidad, \( {q}_{h}\) en psf, a una altura de montaje igual a 8.33 ft.
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\)
\({q}_{h} = 0.00256(0.85)(1.0)(0.85)(0.987)(100)^2 = 18.256 psf\)
\({q}_{h} = 18.256 psf\)
Para calcular la presión del viento de diseño, estaremos usando la ecuación (1). Los detalles de estos parámetros se muestran a continuación..
Factor de Efecto de Ráfaga, \(G\)
En la determinación del factor de efecto de ráfaga, \(G\), primero necesitamos calcular la frecuencia natural fundamental de la estructura \( {n}_{1} \). Si \( {n}_{1} \) es menos que 1 Hz, se clasificará como estructura flexible, por lo tanto tendremos que calcular para \(G\) utilizando la sección 26.11.5. En este ejemplo, para un enfoque simplificado, supondremos que nuestro panel solar es rígido, dónde \(G\) es igual a 0.85 basado en la sección 26.11.1 de ASCE 7-16. Cabe señalar que se necesita la diligencia debida para verificar la frecuencia natural fundamental de la estructura para determinar el factor de efecto de ráfaga, especialmente para estructuras flexibles, ya que magnificará este parámetro..
Coeficiente de presión neta, \({C}_{N}\), Ángulo de inclinación ≤ 45°
Para determinar los coeficientes de presión neta, \( {C}_{N} \), asumiremos el panel solar como un edificio abierto con techo monopendiente. Podemos obtener estos valores de la Figura 27.3-4 de ASCE 7-16 con la suposición de “Flujo de viento claro.” Tenga en cuenta que estos valores solo son aplicables a paneles solares con un ángulo de inclinación menor o igual a 45°
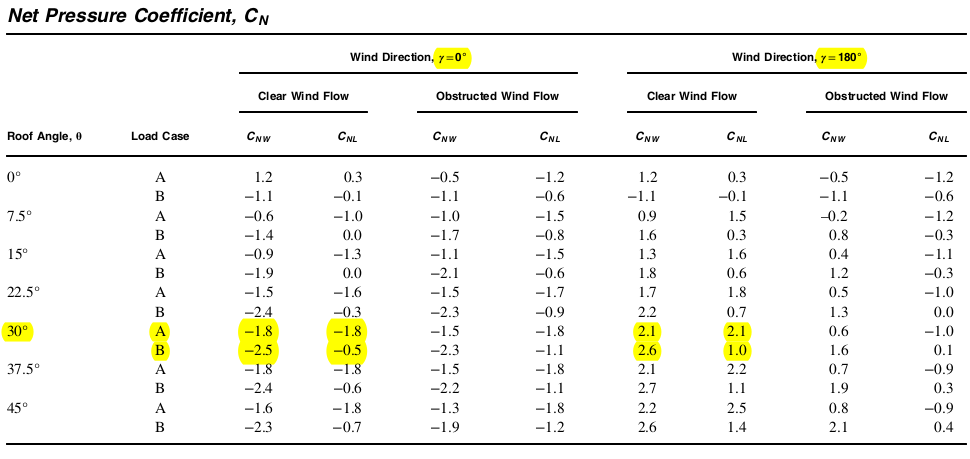
Figura 6. Coeficiente de presión neta, \( {C}_{N} \), a partir de la Figura 27.3-4 de ASCE 7-16 para edificio abierto con tejado a una pendiente.
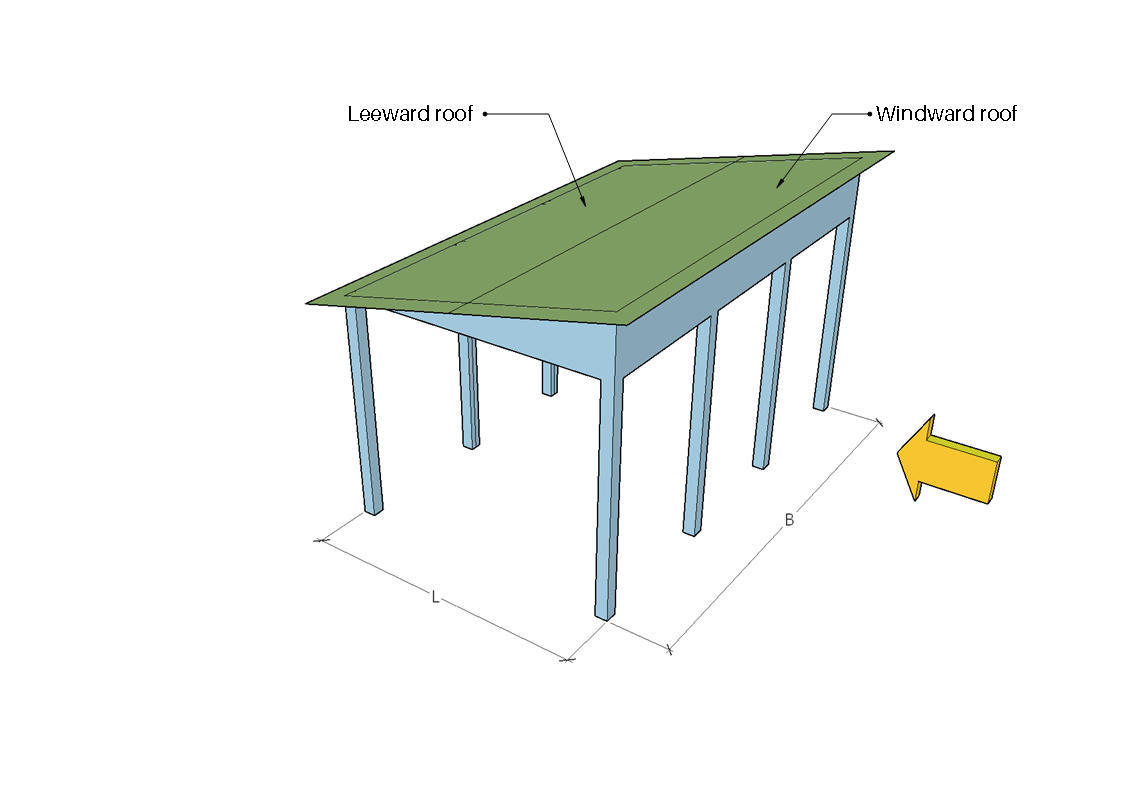
Figura 7. Zonas de barlovento y sotavento para ángulo de dirección igual a 0° .
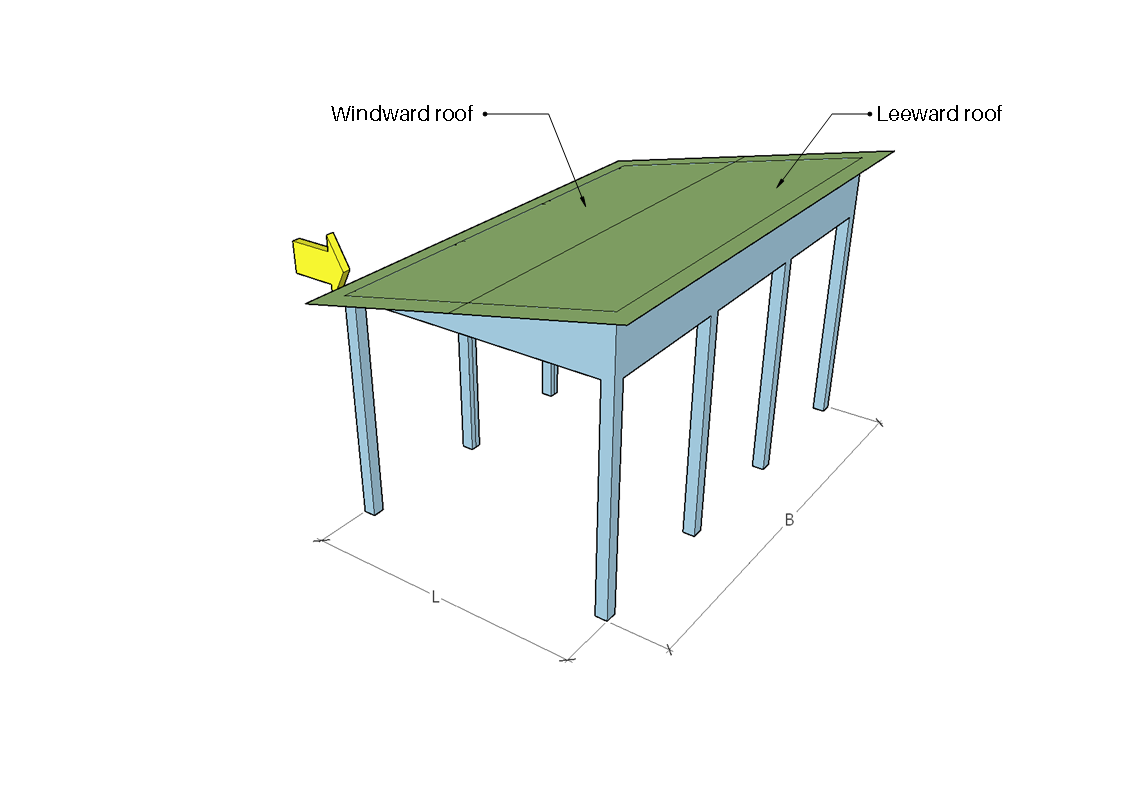
Figura 8. Zonas de barlovento y sotavento para ángulo de dirección igual a 180°.
Dado que el ángulo de inclinación del panel solar es igual a 30°, los correspondientes coeficientes de presión neta, \( {C}_{N} \), a utilizar son los siguientes:
Tabla 4. Valores de \( {C}_{N} \) para ser utilizado en base a la figura 27.3-4 de ASCE 7-16.
| Caso de carga | Dirección = 0° | Dirección = 180° | ||
|---|---|---|---|---|
| \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | |
| A | -1.8 | -1.8 | 2.1 | 2.1 |
| B | -2.5 | -0.5 | 2.6 | 1.0 |
Tenga en cuenta que un valor negativo significa que la presión del viento actúa alejándose de la superficie y un valor positivo indica que la presión del viento actúa hacia la superficie.. De la tabla 4, se puede inferir que consideraremos cuatro (4) casos de carga para carga de viento en nuestro panel solar.
Presiones de viento de diseño – Ángulo de inclinación ≤ 45°
En el cálculo de la carga de viento en paneles solares con ángulo de inclinación > 45°, estaremos usando la ecuación (1), por lo tanto, las cargas de viento en los paneles solares montados en el suelo:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
Tabla 5. Las cargas de viento calculadas en los paneles solares montados en el suelo que se aplicarán a la estructura..
| Caso de carga | Dirección = 0° | Dirección = 180° | ||
|---|---|---|---|---|
| Barlovento, psf |
Sotavento, psf | Barlovento, psf | Sotavento, psf | |
| A | -27.932 | -27.932 | 32.587 | 32.587 |
| B | -38.794 | -7.759 | 40.346 | 15.518 |
Por lo tanto, las cargas de viento en los paneles solares montados en el suelo cuando se aplican son las siguientes:
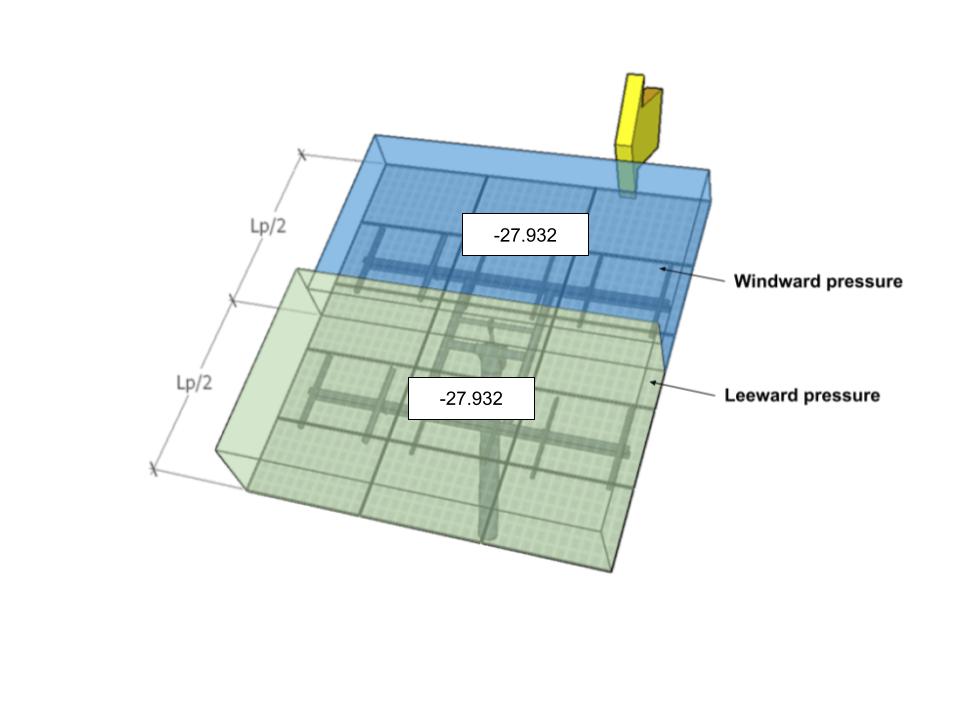
Figura 9. Presiones de viento de diseño para ángulo de dirección 0° – Caso de carga A.
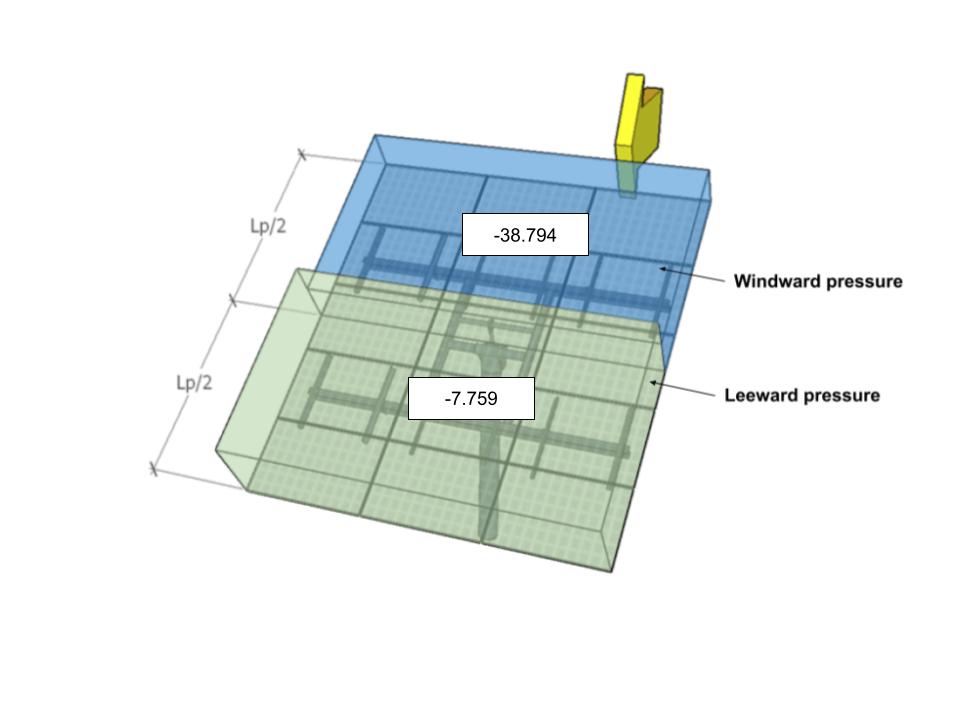
Figura 10. Presiones de viento de diseño para ángulo de dirección 0° – Caso de carga B.
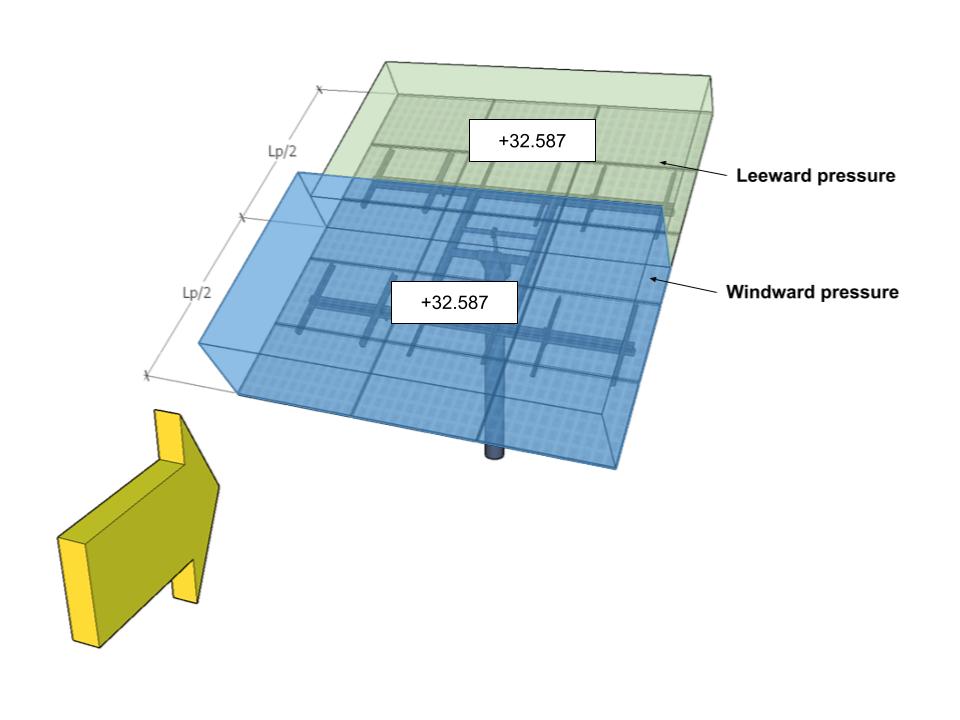
Figura 11. Presiones de viento de diseño para un ángulo de dirección de 180° – Caso de carga A.
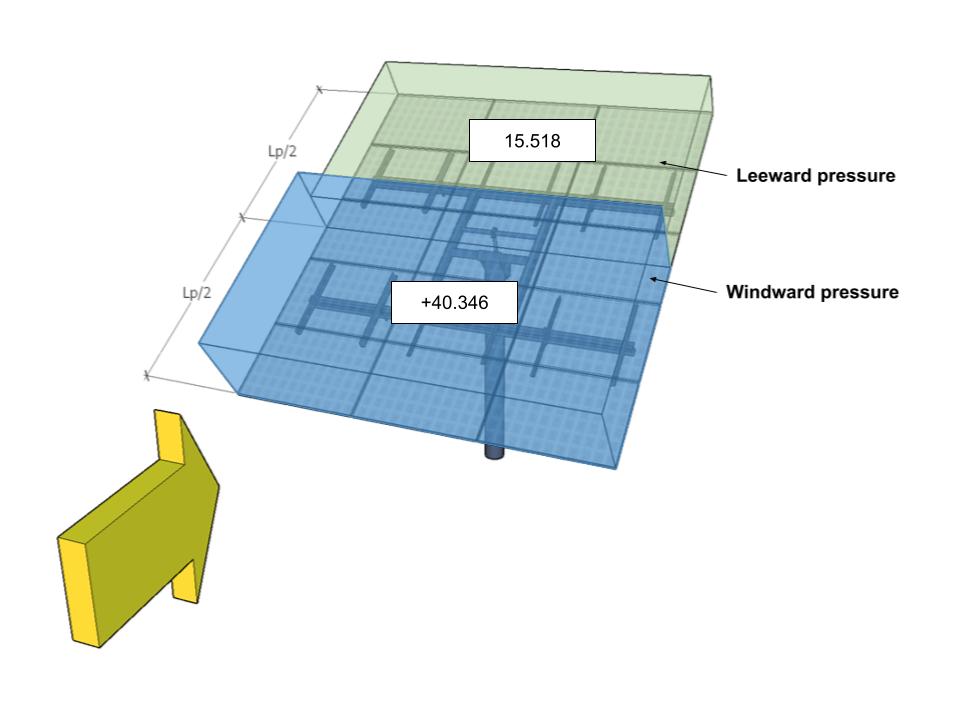
Figura 12. Presiones de viento de diseño para un ángulo de dirección de 180° – Caso de carga B.
Coeficiente de fuerza neta, \({C}_{f}\), – Las dimensiones del panel solar > 45°
Digamos que nuestro ángulo de inclinación del panel solar se cambió a 60°. Necesitamos usar la proyección vertical del panel solar y considerarlo como un signo sólido con la presión de velocidad calculada hasta la parte superior de esta proyección..
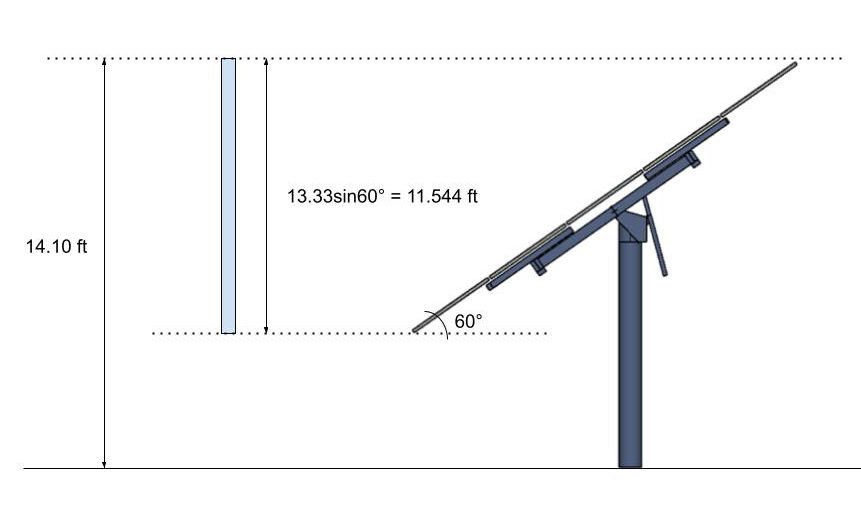
Figura 13. La proyección vertical del panel solar para ser considerado como signo sólido..
Dado que la altura desde el suelo hasta la parte superior del proyecto sigue siendo menor que 15 ft, todavía podemos usar nuestro calculado \( {K}_{z}\) encima. Por lo tanto, el valor calculado de \( {q}_{h}\) seguiría siendo el mismo. La red para el coeficiente, \( {C}_{f}\), a utilizar se puede obtener de la Figura 29.3-1 de ASCE 7-16. Además, en el cálculo de estos coeficientes de fuerza, solo consideraremos el Caso A para un enfoque simplificado. De la figura 29.3-1:
\({q}_{h} = 18.256 psf\)
\( B = 16.25 ft\)
\( s = 11.544 ft\)
\( h = 14.102 ft\)
\( s/h = 0.818\)
\( B/s = 1.408\)
A partir de los valores tabulados de \( {C}_{f} \) En figura 29.3-1, interpolaremos los valores conocidos de \( B/s \) igual a 1 y 2, y \( s/h \) igual a 0.9 y 0.7.
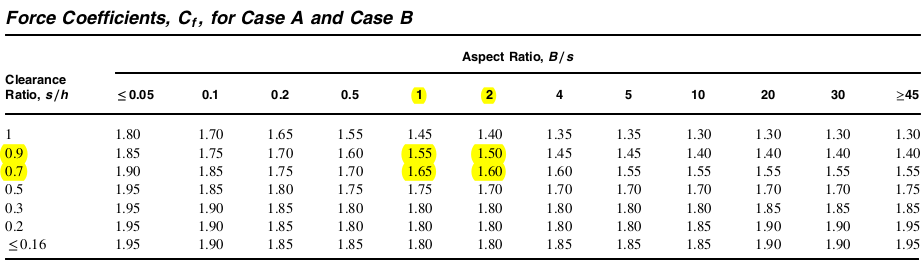
Figura 14. Coeficiente de fuerza neta, \( {C}_ _{F} \), a partir de la Figura 29.3-1 de ASCE 7-16 para señales sólidas.
Al interpolar los valores resaltados para obtener \( {C}_{f} \) de nuestro \( B/s \) y \( s/h \), obtenemos:
\( {C}_{f} = 1.5706 \)
Presiones de viento de diseño – Las dimensiones del panel solar > 45°
En el cálculo de la carga de viento en paneles solares con ángulo de inclinación > 45°, estaremos usando la ecuación (2), por lo tanto, las cargas de viento en los paneles solares montados en el suelo:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
\( {C}_{f} = 1.5706 \)
\(p = {q}_{h}G{C}_{f} = (18.256)(0.85)(1.5706) = 24.372 psf\)
\(p = 24.372 psf\)
Por lo tanto, las cargas de viento en los paneles solares montados en el suelo cuando se aplican: 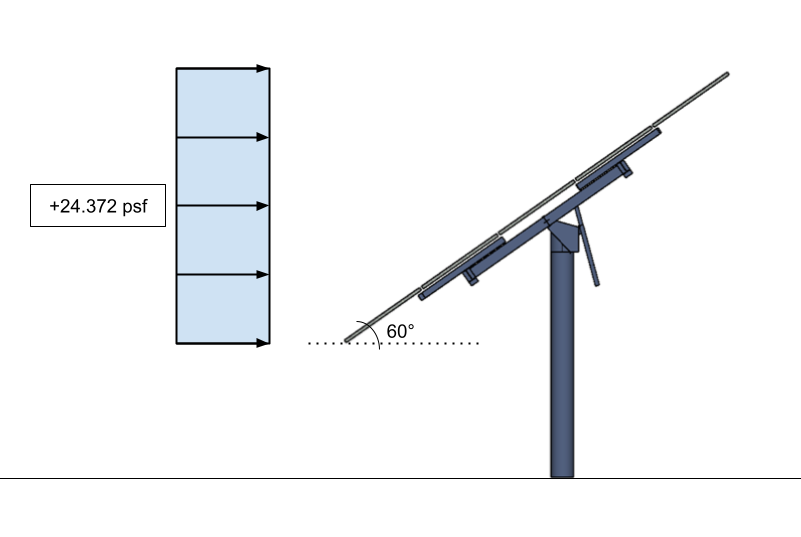
Figura 15. La presión del viento de diseño para el panel solar como señal sólida – aplicado a la proyección vertical.
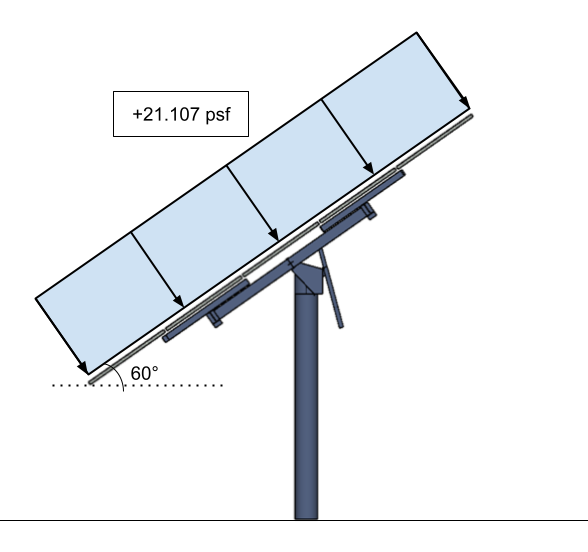
Figura 16. La presión del viento de diseño convertida para el panel solar como señal sólida – aplicado a la superficie del panel solar.
Todos los cálculos de viento se pueden realizar utilizando SkyCiv Load Generator para ASCE 7-16 (calculadora de carga de viento del panel solar). Los usuarios pueden ingresar la ubicación del sitio para obtener la velocidad del viento y los datos del terreno, ingrese los parámetros del panel solar y genere las presiones de viento de diseño. Con la versión independiente, puede optimizar este proceso y obtener un informe detallado de cálculo de carga de viento para paneles solares!
Carga de nieve
Para áreas que experimentan nieve, También se deben considerar las cargas de nieve en el panel solar.. Para calcular las cargas de nieve para nuestro panel solar, estaremos usando el capítulo 7 de ASCE 7-16. Consideraremos la estructura del panel solar como un edificio con techo de una sola pendiente y solo consideraremos la carga de nieve balanceada (carga de nieve de techo inclinado). Las fórmulas para determinar la carga de nieve para nuestro panel solar son las siguientes:
Para calcular la carga de nieve del techo plano \({p}_{f} \):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \) (7)
Dónde:
\({C}_{e} \) = factor de exposición
\({C}_{t} \) = factor térmico
\({I}_{s} \) = factor de importancia para la carga de nieve
\({p}_{g} \) = carga de nieve en el suelo, en psf
Para calcular la carga de nieve del techo inclinado \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \) (8)
Dónde:
\({C}_{s} \) = factor de pendiente del techo
\({p}_{r} \) = carga de recargo por lluvia sobre nieve
Factor de exposición, \({C}_{e} \)
El factor de exposición, \({C}_{e} \), se puede determinar a partir de la tabla 7.3-1 de ASCE 7-16 basado en la rugosidad de la superficie y la exposición del techo. De la imagen satelital de la ubicación que obtuvimos de Google Maps, podemos clasificar que la ubicación es Rugosidad de la superficie C (terreno abierto con obstrucciones dispersas que tienen alturas generalmente menores a 30 ft) y con el supuesto de que los paneles solares son completamente expuesto y sin obstrucciones. Por lo tanto, la Factor de exposición, \({C}_{e} \), de la estructura es igual a 0.9.
Factor Térmico, \({C}_{t} \)
El factor térmico, \({C}_{t} \), se puede determinar a partir de la tabla 7.3-2 de ASCE 7-16 basado en la condición térmica de la estructura durante el invierno. De la mesa, podemos clasificar nuestro panel solar como “Estructuras sin calefacción y al aire libre.” Por lo tanto, el correspondiente de Factor Térmico, \({C}_{t} \), es para la estructura es igual a 1.2.
Factor de importancia para la carga de nieve, \({I}_{s} \)
El factor de importancia para la carga de nieve, \({I}_{s} \), se puede determinar a partir de la tabla 1.5-2 de ASCE 7-16 en función de la Categoría de Riesgo de la estructura. Dado que la estructura está clasificada como Categoría de Riesgo I, de la mesa, \({I}_{s} \) es igual a 0.8.
Carga de nieve en el suelo, \({p}_{g} \)
La carga de nieve en el suelo, \({p}_{g} \), se puede determinar a partir de la figura 7.2-1 de ASCE 7-16 Como se muestra abajo. De esta figura, la carga de nieve del suelo, \({p}_{g} \) para nuestro panel solar es igual a 10 psf.
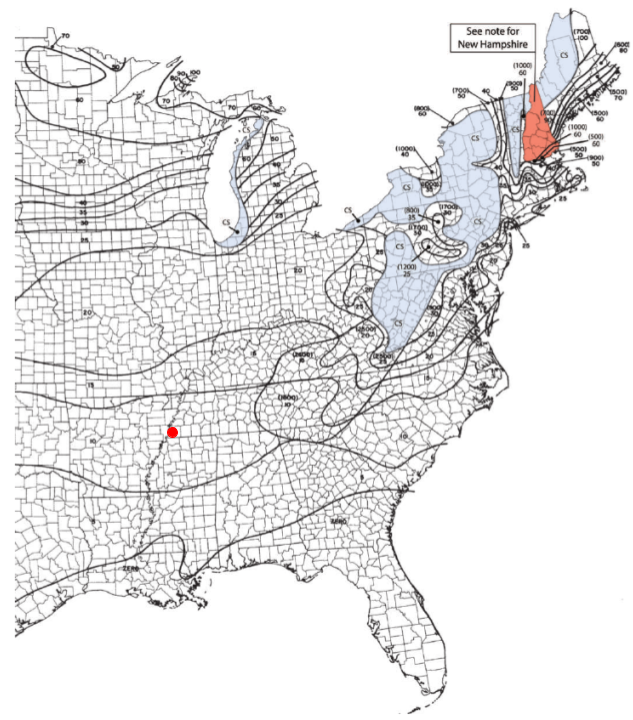
Figura 17. Mapa de carga de nieve en el suelo de la figura 7.2-1 de ASCE 7-16 con punto rojo para indicar la ubicación de nuestro panel solar.
SkyCiv también automatiza los cálculos de carga de nieve en el suelo con algunos parámetros. Pruebe nuestro Calculadora de carga de viento del panel solar
Carga de nieve en techo plano, \({p}_{f} \)
De los parámetros anteriores, ya podemos calcular la carga de nieve del techo plano, \({p}_{f} \), usando la ecuación (7):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \)
\({p}_{f} = 0.7(0.9)(1.2)(0.8)(10) = 6.048 psf \)
\({p}_{f} = 6.048 psf \)
Factor de pendiente del techo, \({C}_{s} \)
El factor de pendiente del techo se puede calcular a partir de la Figura 7.4-1 de ASCE 7-16 dependiendo del ángulo de inclinación, la obstrucción debajo de la superficie del techo, y el valor del factor térmico \({C}_{t} \). Para nuestro panel solar, supondremos que nuestro panel solar está clasificado como “Superficie resbaladiza.” Dado que el factor térmico \({C}_{t} \) es igual a 1.2, ya podemos interpolar el valor de \({C}_{s} \) de 7-2c. Del gráfico, los valores conocidos son:
\({C}_{s} = 1.0 \) for 15°
\({C}_{s} = 0.0 \) for 70°
Interpolando estos valores podemos obtener:
\({C}_{s} = 0.727 \) for 30°
Por lo tanto, \({C}_{s} = 0.727 \) para nuestro panel solar.
Carga con recargo por lluvia sobre nieve, \({p}_{r} \)
Un adicional de 5 carga psf de recargo por lluvia sobre nieve, \({p}_{r} \), debe ser considerado para lugares donde \({p}_{g} \) es menor o igual que 20 psf pero no cero, para todos los techos con ángulo de inclinación (en grados) con menos de \( W/50 \) grados donde \( W \) es la distancia horizontal desde el alero hasta la cumbrera. El valor de \({p}_{r} \) solo se aplica al techo inclinado (equilibrado) caso de carga. En este ejemplo:
\(W = 13.33 cos 30° = 11.544 ft \)
\( W/50 =0.231° \)
Ya que \({p}_{g} = 10 psf \) pero el ángulo de inclinación 30° es mayor que \( W/50 =0.231° \), \({p}_{r} \) puede despreciarse y es igual a 0.0
Carga de nieve de techo inclinado, \({p}_{s} \)
A partir de la Ecuación (8), podemos calcular la carga de nieve del techo inclinado \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \)
\({p}_{s} = (0.727)(6.048) + 0.0 = 4.397 psf \)
\({p}_{s} = 4.397 psf \)
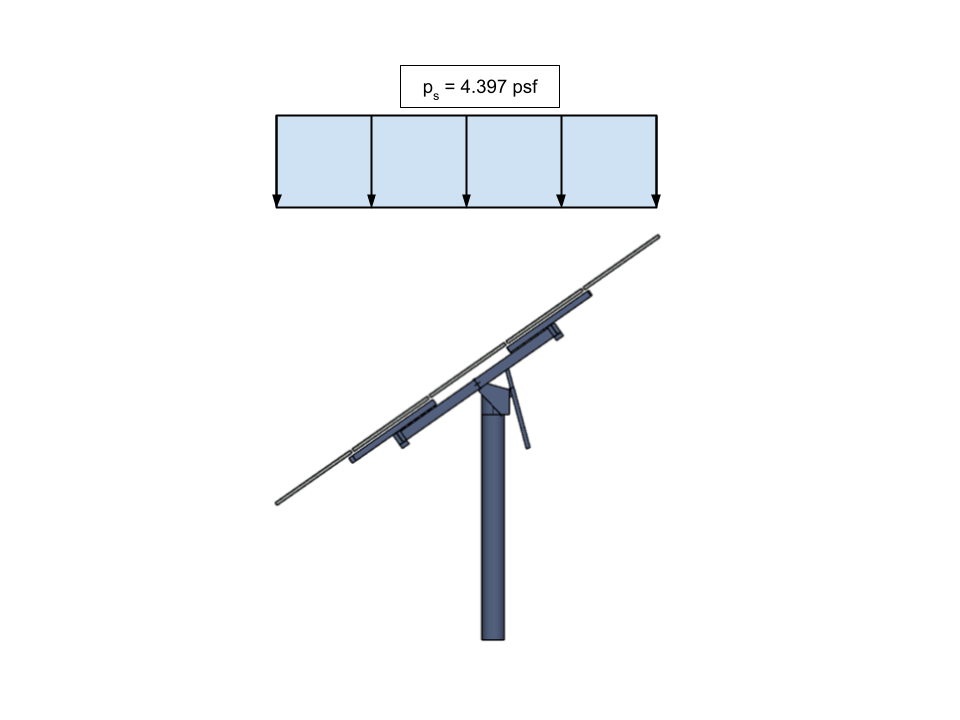
Figura 18. La carga de nieve equilibrada calculada (carga de nieve de techo inclinado) para el panel solar aplicado sobre la proyección horizontal de la estructura.
Tenga en cuenta que \({p}_{s} \) se aplica sobre la proyección horizontal de la estructura. Tendremos que convertir este valor a una carga de presión inclinada equivalente para poder aplicarlo a nuestro modelo.
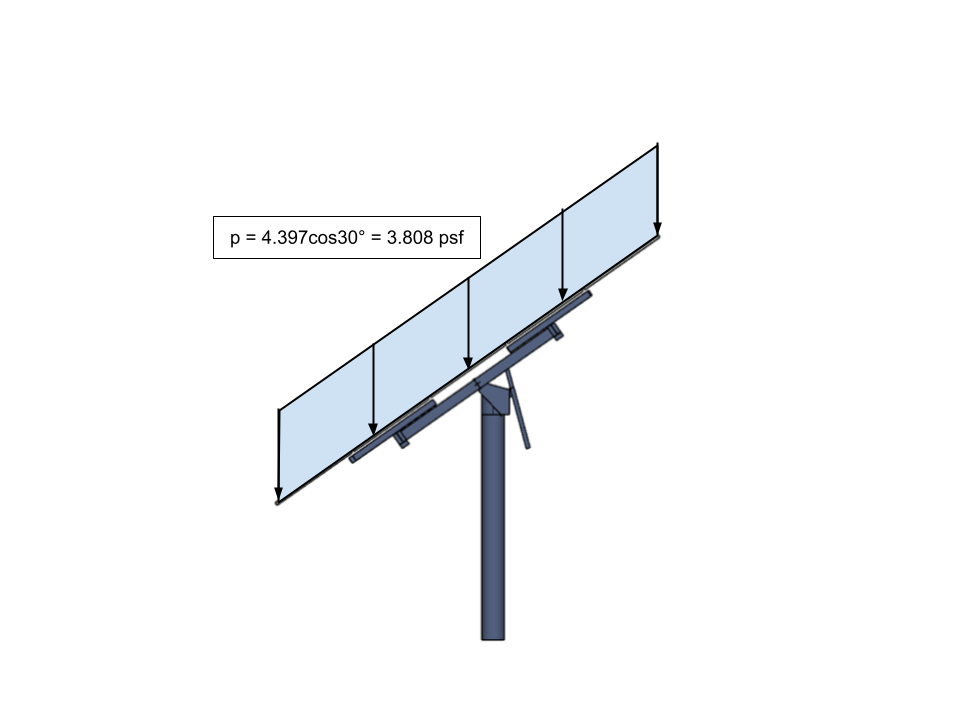
Figura 19. La carga de nieve equilibrada convertida (carga de nieve de techo inclinado) para que el panel solar se aplique a nuestro modelo.
Los cálculos de carga de nieve también se pueden realizar en SkyCiv Load Generator para ASCE 7-16. sin embargo, solo está disponible en nuestra versión independiente y cuenta profesional.
Generador de carga SkyCiv
Uso del generador de carga SkyCiv, puede obtener cargas de viento y nieve en paneles solares montados en el suelo con solo unos pocos clics y entradas. Cuando compra la versión independiente o se registra para una cuenta Profesional, podrá generar el informe detallado de cálculos de viento y nieve para su proyecto de panel solar!
Puede consultar el informe detallado de carga de viento y nieve para el panel solar a través de estos enlaces:
además, También puede crear su propia calculadora de carga de viento del panel solar utilizando la API del generador de carga de SkyCiv, tal como creamos una solución para uno de nuestros clientes.. Con solo unas pocas entradas, diseñará automáticamente el sistema de paneles solares para usted. Puede consultar la documentación de nuestra API a través de este enlace.
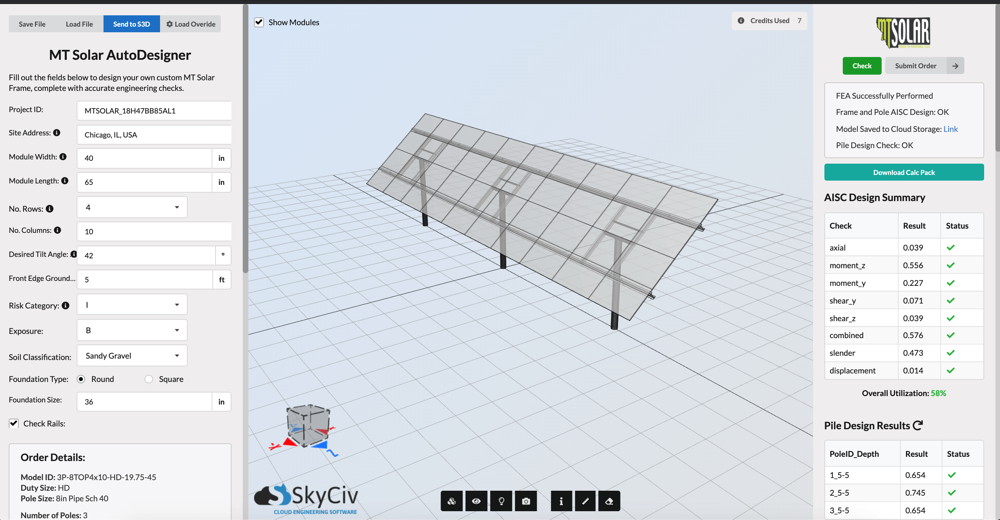
Figura 20. Nuestra solución personalizada para paneles solares creada para MT Solar utilizando SkyCiv API.
Para recursos adicionales, puedes usar estos enlaces:
- Introducción al generador de carga SkyCiv
- ASCE 7-16 Cálculos de carga de viento (Paneles solares)
- ASCE 7 Cálculos de carga de nieve
- Cómo calcular y aplicar cargas de deriva de nieve en el techo con ASCE 7-10
- Cálculo de cargas de nieve en el techo con ASCE 7-10
Ingeniero estructural, Desarrollo de Producto
Maestría en Ingeniería Civil
Referencias:
- Coulbourne, W. L., & Stafford, T. E. (2020, abril). Cargas de viento: Guía de las disposiciones de carga de viento de ASCE 7-16. Sociedad Americana de Ingenieros Civiles.
- Sociedad Americana de Ingenieros Civiles. (2017, junio). Cargas mínimas de diseño y criterios asociados para edificios y otras estructuras.. Sociedad Americana de Ingenieros Civiles.
- mapas de Google
- MT Solar



