Un recorrido y un ejemplo de cálculo de cargas de deriva de nieve y cómo aplicarlas
Los diseños de techos generalmente presentan multitud de elevaciones de techos y rara vez ofrecen una sola altura de techo. Debido a esto, Hay áreas de techo más altas y más bajas entre sí y están sujetas a la nieve.. La cantidad de carga adicional de nieve., o recargo, puede y tendrá un gran impacto en el diseño de los miembros en estas áreas.
La geometría del techo y la dirección del viento son los dos factores que conducen a la nieve.. Las dos direcciones del viento que causan derivas de nieve son “barlovento” y “sotavento”. Las corrientes de nieve de barlovento ocurren cuando el viento sopla nieve desde un techo de menor elevación hacia la pared de un edificio adyacente, techo más alto. Las desviaciones de nieve de sotavento ocurren cuando el viento sopla la nieve de un techo de mayor elevación hacia un techo inferior adyacente. Ver figura 7-7 según ASCE 7-10 a continuación para una descripción sucinta:

Asumamos que nuestro proyecto está en Madison, Wisconsin y ya hemos calculado nuestro equilibrio, carga de nieve en el techo aquí. De nuestro ejemplo, se descubrió que nuestra carga de tierra y la carga de nieve del techo plano eran 30 psf y 21 psf, respectivamente. Las disposiciones sobre cómo calcular el recargo por deriva de nieve para estructuras se pueden encontrar en la Sección 7.8 de ASCE 7-10.
El techo de nuestra estructura de ejemplo tiene dos alturas de techo diferentes y, por lo tanto, necesitamos calcular el recargo por deriva de nieve y aplicarlo a nuestros miembros. En nuestro caso, nuestras vigas están espaciadas en 10 pies.
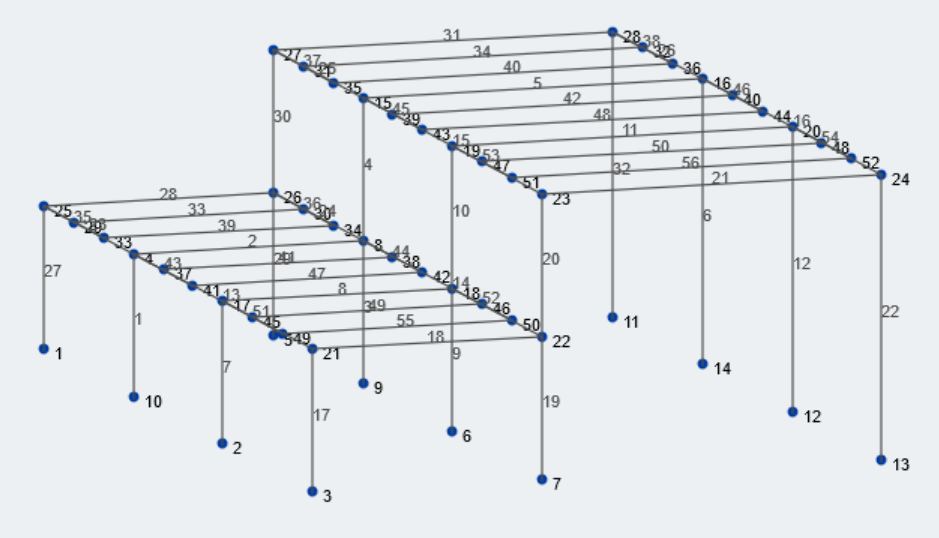
Figura 1: Vista isométrica de nuestra estructura de ejemplo.
Primero recopilemos la información geométrica relevante sobre nuestra estructura. El tamaño de la bahía inferior y superior es 25 pies y 37 pies, respectivamente. Las elevaciones de techo más bajas y más altas son 15 pies y 30 pies de grado, respectivamente. La mayoría de los valores geométricos pueden asociarse con variables.. Veamos todas las variables pertinentes para este cálculo..
\({pag}_ _{gramo}\) = carga de nieve en el suelo
\({l}_ _{tu}\) = longitud del techo superior
\({l}_ _{l}\) = longitud del techo inferior
\({h}_ _{d}\) = altura de la deriva de nieve
\({w}\) = ancho de deriva de nieve
\({h}_ _{b}\) = altura de carga de nieve equilibrada
\({h}_ _{c}\) = altura libre desde la parte superior de la carga de nieve equilibrada hasta el punto más cercano del techo adyacente
\({h}_ _{r}\) = diferencia de altura entre techos
\({pag}_ _{s}\) = diseño de carga de nieve del Capítulo 7
\({C}\) = densidad de nieve
\({pag}_ _{d}\) = carga de deriva de nieve
Echa un vistazo a la figura 7-8 según ASCE 7-10 para una descripción de muchos de estos términos y lo que representan visualmente:
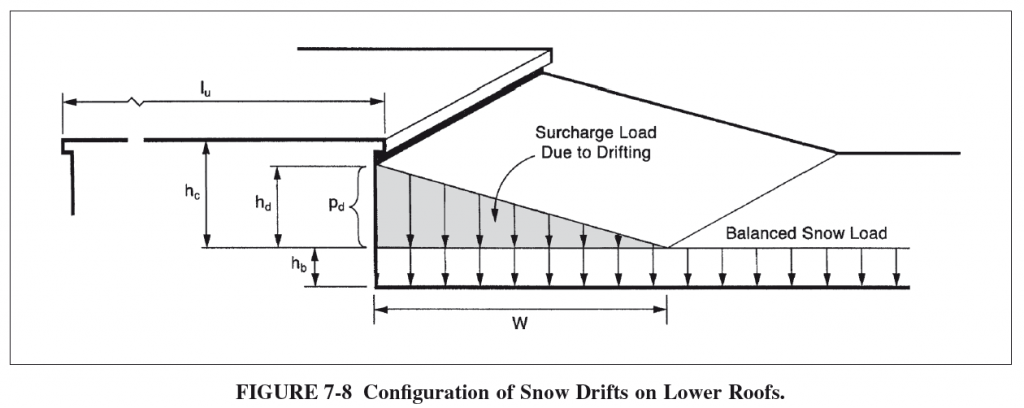
Encontrar la carga de recargo de deriva de nieve
Ahora que hemos identificado cuáles son las variables, las configuraciones de carga de nieve, y las restricciones geométricas de nuestra estructura, vamos a calcular la deriva de nieve.
primero, averiguar si es necesario cargar nieve, para ASCE 7.7-1:
Si \({h}_ _{c}/{h}_ _{b} < 0.2\), entonces la aplicación de nieve no es necesaria.
\({h}_ _{b} = {pag}_ _{s}/{C}\), dónde:
\({C} = 0.13{pag}_ _{gramo} + 14 ≤ 30 pcf\)
\({C} = 0.13*(30) + 14 = 17.9 pcf ≤ 30 pcf \)
\({h}_ _{b} = {21 psf}/{17.9 pcf } = 1.17 ft\)
\({h}_ _{c} = {h}_ _{r}-{h}_ _{b}\)
\({h}_ _{c} = 15 ft – 1.17 ft = 13.8 ft\)
\({h}_ _{c}/{h}_ _{b} = 13.8 ft / 1.17ft = 11.8 > 0.2\) y por lo tanto, la carga de nieve es necesaria.
Segundo, encontrar la altura máxima de deriva entre las direcciones de barlovento y sotavento:
La altura de la deriva para ambas direcciones del viento se puede encontrar usando la ecuación que se encuentra en la Figura 7-9 de ASCE 7-10, mostrada a continuación:
\({h}_ _{d} = 3/4*(0.43({l}_ _{l})^{1/3}({p_g}+10)^{1/4}-1.5)\) para la deriva de barlovento
\({h}_ _{d} = 0.43({l}_ _{tu})^{1/3}({p_g}+10)^{1/4}-1.5\) para la deriva de sotavento
Altura de deriva de barlovento:
\({h}_ _{d} = 3/4 *(0.43(25 ft)^{1/3}(30 psf + 10)^{1/4}-1.5)\)
\({h}_ _{d} = 1.25 ft\)
Altura de deriva de sotavento:
\({h}_ _{d} = 0.43(37 ft)^{1/3}(30 psf + 10)^{1/4}-1.5\)
\({h}_ _{d} = 2.1 ft\)
La altura de deriva máxima entre la altura de deriva de barlovento y sotavento se utilizará para el diseño., por lo tanto:
\({h}_ _{d} = 2.1 ft\)
próximo, encontrar el ancho del recargo por deriva de nieve:
El ancho de la carga de deriva de nieve, \({w}\), depende de \({h}_ _{c}\) y \({h}_ _{d}\)
Por sección 7.7.1,
Si \({h}_ _{d} ≤ {h}_ _{c}\), luego \({w} = 4{h}_ _{d}\)
Si \({h}_ _{d} > {h}_ _{c}\), luego \({w} = 4{h}_ _{d}^ 2 /{h}_ _{c}) y posteriormente \({h}_ _{d} = {h}_ _{c}\)
En nuestro caso, \({h}_ _{c} = 13.8 ft\) y \({h}_ _{d} = 2.1 ft\), y por lo tanto:
\({h}_ _{d} ≤ {h}_ _{c}\), y
\({w} = 4*(2.1 ft)\)
\({w} = 8.4 ft\)
Nota, para ASCE 7-10 la el ancho de la deriva de nieve nunca debe exceder \(8{h}_ _{c}\)
Último, calcular la carga de recargo por deriva de nieve:
Para encontrar la carga máxima de recargo, multiplicar la altura de deriva por la densidad de nieve:
\({pag}_ _{d} = {h}_ _{d}{C}\)
En nuestro caso,
\({pag}_ _{d} = (2.1 ft)*(17.9 pcf )\)
\({pag}_ _{d} = 37.6 psf\)
La carga máxima de recargo por deriva de nieve se superpone a la carga de nieve equilibrada:
\({pag}_ _{max} = {pag}_ _{d}+{pag}_ _{s}\)
\({pag}_ _{max} = 58.6 psf\)
Aplicación de las cargas de recargo de deriva de nieve
Veamos el marco medio de nuestra estructura.. El área distribuida para las vigas en este plano es 10 ft debido a la constante 10 ft espacio de haz. Figura 2 a continuación se muestra la carga de nieve equilibrada de 21 psf aplicado al techo de nuestra estructura. Nota, todos los valores no están factorizados, cargas de servicio.
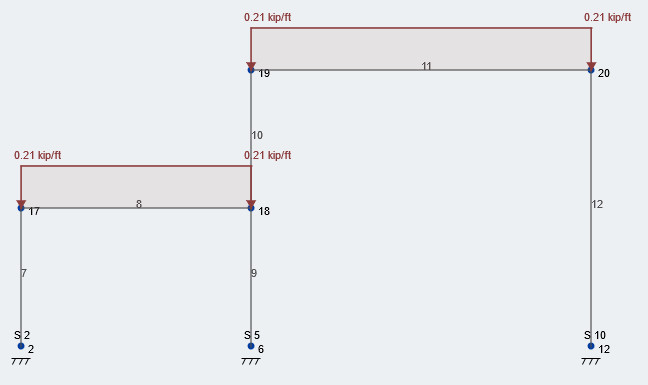
Figura 2: Condición de carga típica de carga de nieve equilibrada
Ahora, tomemos la carga del recargo por deriva de nieve y superpongamosla en nuestra estructura. Figura 3 representa la carga de deriva adicional en la ubicación correcta. Como puedes ver, nuestra carga total de nieve es 58.6 psf – redondeado a 59 psf – ubicado en la cara de la pared y luego disminuye linealmente sobre el 8.4 ancho de deriva ft de nuevo a la carga de nieve equilibrada constante. Esta condición de carga sigue toda la longitud de la pared., en nuestro curso, la longitud de la estructura.
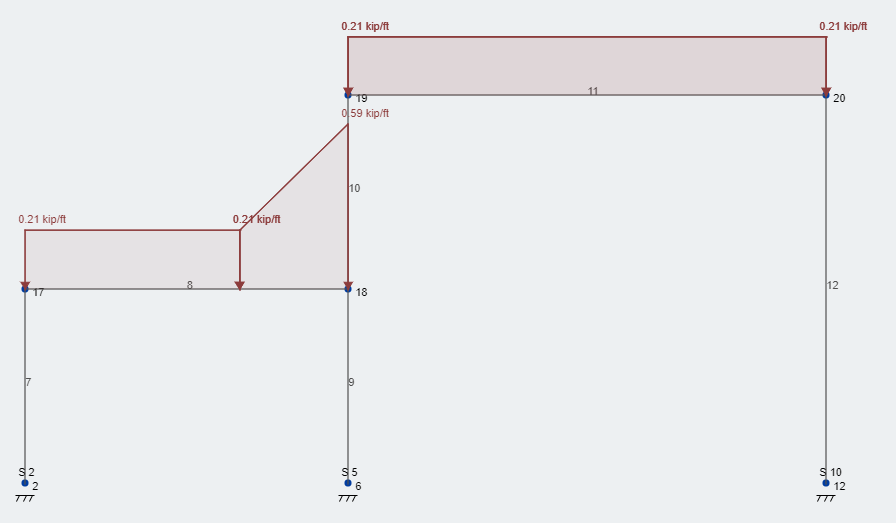
Figura 3: Condición de carga típica nivel de servicio cargas de diseño de nieve
En este punto, las cargas de nieve están listas para el análisis en conjunto con otros casos de carga y combinaciones de carga basadas en ASCE 7-10 y otros códigos de construcción pertinentes. Asegúrese de leer el capítulo 7 de ASCE 7-10 Para obtener más información sobre las disposiciones sucesivas para la carga parcial de nieve y la carga de nieve no balanceada, ya que esas condiciones no fueron evaluadas aquí.
Referencias:
- Cargas mínimas de diseño para edificios y otras estructuras. (2013). ASCE / SEI 7-10. Sociedad Americana de Ingenieros Civiles.


