Un ejemplo completamente trabajado de AS / NZS 1170.2 (2011) cálculos de carga de viento
SkyCiv's calculadora de carga de viento calculadora de carga de viento. En este artículo, calcularemos la presión del viento de diseño para una estructura de almacén. Usaremos un modelo de nuestro S3D para demostrar cómo las cargas (COMO 1170.2 / NZS1170.2:2011 ) se aplican en cada superficie.
Tenga en cuenta que el siguiente ejemplo se basa en el 2011 versión del AS/NZS 1170.2. Los procedimientos para la última versión pueden ser diferentes, pero aún así deberían ser similares en el cálculo..
Figura 1. Modelo de almacén en SkyCiv S3D como ejemplo.
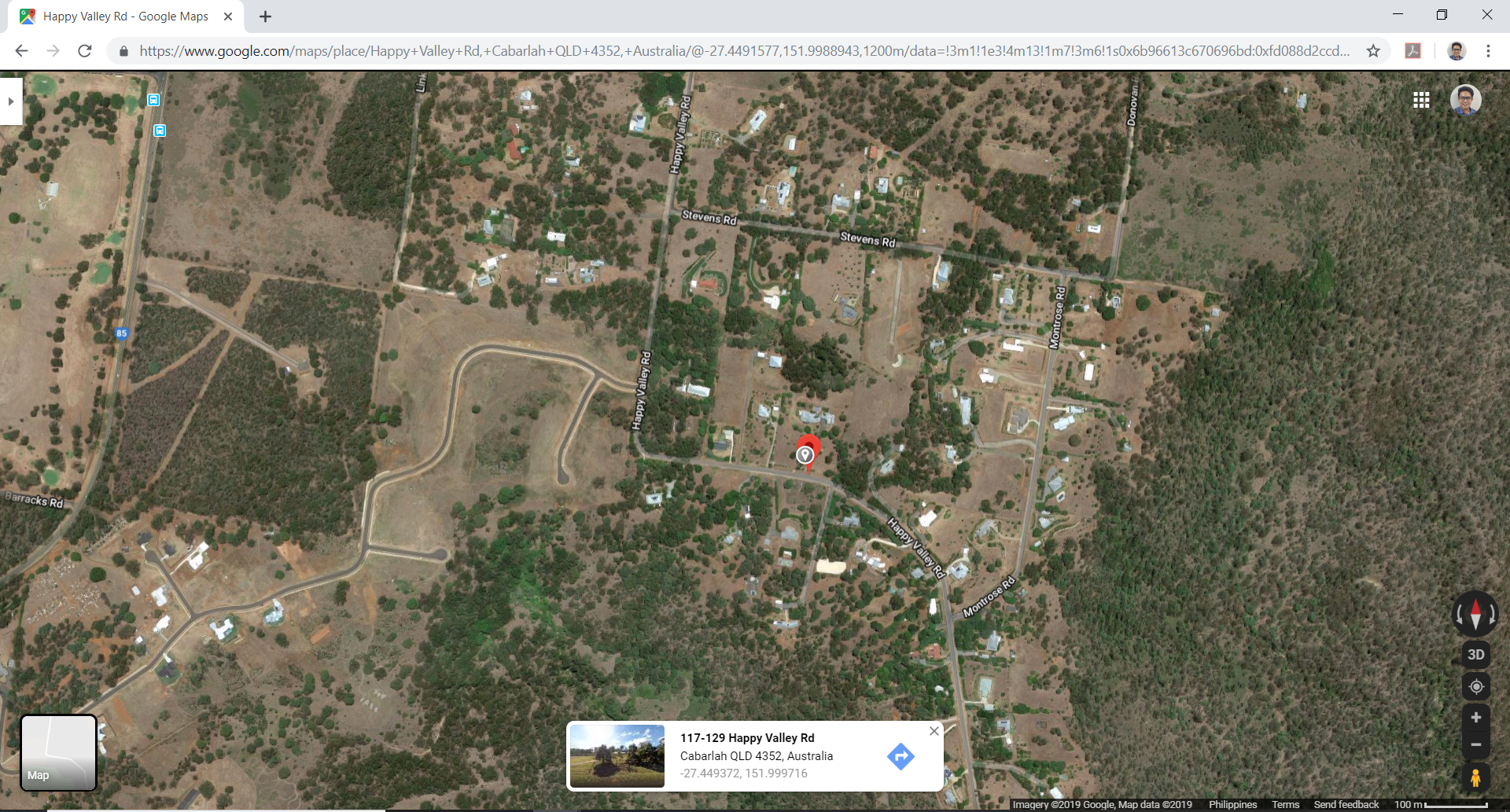
Figura 2. Ubicación del sitio (de Google Maps).
Tabla 1. Datos de construcción necesarios para nuestro cálculo del viento.
| Ubicación | Happy Valley Road, Desafiarlo, Queensland, Australia |
| Ocupación | Miscelánea – Estructura de almacén |
| Terreno | Campo plano |
| Dimensiones | 19.507 m (L) × 31.699 m (B) en plan Altura del alero 9.144 m Altura del ápice. 10.973 m Inclinación del techo 3:16 (10.62°) Sin abrir |
| Revestimiento | Correas espaciadas en 0.6 m Tacos de pared espaciados en 0.6 m |
La fórmula para determinar la presión del viento de diseño son:
Para la velocidad del viento de diseño:
\({V }_ _{sentar,si} = {V }_ _{R} {M}_ _{d} {M}_ _{z,gato} {M}_ _{s} {M}_ _{t} \) (1)
Dónde:
\({V }_ _{sentar,si}\) = velocidad del viento de diseño en m / s
\({V }_ _{R}\) = velocidad del viento ráfaga regional 3s (del mapa del viento), em (AS / NZS 1170.2 Sección de 3)
\({M}_ _{d}\)= multiplicador direccional del viento para 8 direcciones cardinales (si) (AS / NZS 1170.2 Sección de 3)
\({M}_ _{z,gato}\) = multiplicador de terreno / altura (AS / NZS 1170.2 Sección de 4)
\({M}_ _{s}\)= multiplicador de blindaje, ajustado a 1.0 (AS / NZS 1170.2 Sección de 4)
\({M}_ _{t}\)= multiplicador topográfico (AS / NZS 1170.2 Sección de 3)
Para la presión del viento de diseño:
\(p = 0.5 {⍴}_ _{aire} ({V }_ _{desde,θ})^ 2 {C}_ _{higo} {C}_ _{hombre} \) (2)
Dónde:
\(pags) = presión de viento de diseño en Pa
\({⍴}_ _{aire}\) = densidad del aire (1.2 kg / cu.m.)
\({V }_ _{desde,θ}\)= construir velocidades de viento de diseño ortogonal
\({C}_ _{hombre}\)= factor de respuesta dinámico, ajustado a 1.0
\({C}_ _{higo}\) = factor de forma aerodinámica (para presión interna o externa) para edificios cerrados donde:
\({C}_ _{higo,i} = {C}_ _{pag,i} {K}_ _{c,i} \) – para presiones internas (3)
\({C}_ _{higo,mi} = {C}_ _{pag,mi} {K}_ _{a} {K}_ _{c,mi} {K}_ _{l} {K}_ _{pag}\) – para presiones externas (4)
\({C}_ _{pag,i}\) = Coeficiente de presión interna
\({K}_ _{c,i}\) = factor de combinación aplicado a presiones internas
\({C}_ _{pag,mi}\) = coeficiente de presión externa
\({K}_ _{a}\) = factor de reducción de área
\({K}_ _{c,mi}\) = factor de combinación aplicado a presiones externas
\({K}_ _{l}\) = factor de presión local
\({K}_ _{pag}\) = factor de revestimiento poroso
Cada parámetro se discutirá más adelante..
Velocidad regional del viento, \({V }_ _{R}\)
Los datos regionales de velocidad del viento se detallan en la figura 3.1 de la AS / NZS 1170.2 (como se muestra en las figuras 3 y 4 a continuación). Cada área administrativa se clasifica en regiones de velocidad del viento con la velocidad del viento correspondiente. Para nuestro ejemplo, el sitio está ubicado cerca del punto rojo y está clasificado como Región A4 ya que es aproximadamente 106 km del litoral liso de la isla principal de Australia. La velocidad del viento correspondiente se puede calcular usando la tabla 3.1 de AS / NZS 1170.2 como se muestra en la figura 5. El intervalo de recurrencia anual se selecciona según el nivel de importancia y la vida laboral de diseño de la estructura como se detalla en la Tabla 3.3 de AS / NZS 1170.0.
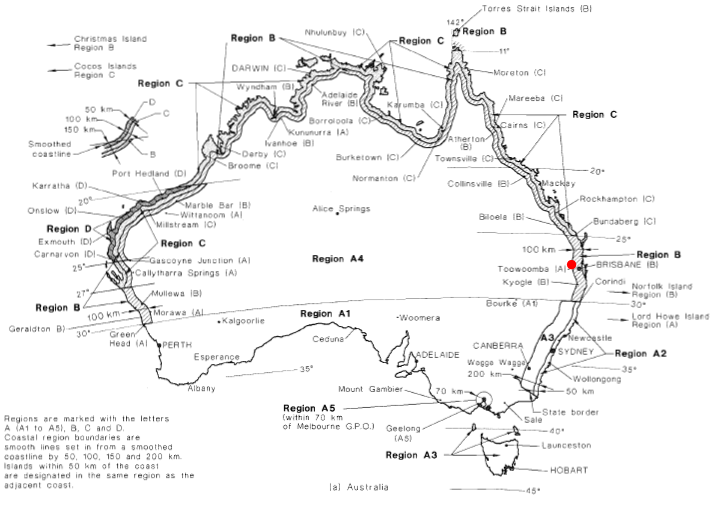
Figura 3. Mapa regional de velocidad del viento para Australia (Figura 3.1(A) de AS / NZS 1170.2).
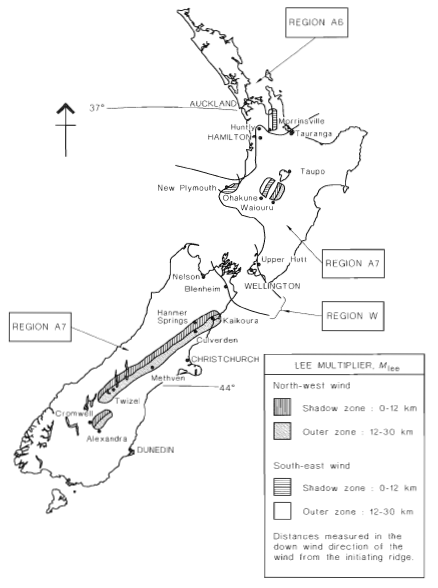
Figura 4. Mapa regional de velocidad del viento para Nueva Zelanda (Figura 3.1(B) de AS / NZS 1170.2).
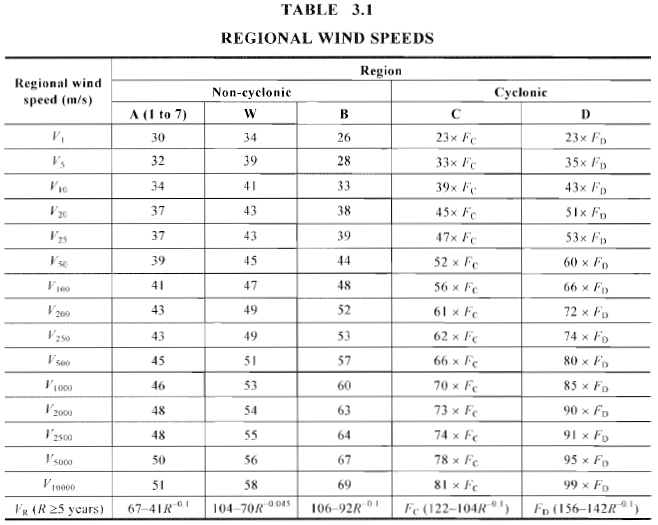
Figura 5. Velocidad del viento correspondiente basada en la región del viento y el intervalo de recurrencia anual (Tabla 3.1 de AS / NZS 1170.2).
Para los estados límite definitivos o de servicio, Mesas 3.1 y 3.3 de AS / NZS 1170.0 (Cifras 6 y 7) detalla cómo clasificar la estructura por nivel de importancia y su correspondiente probabilidad anual de superación.
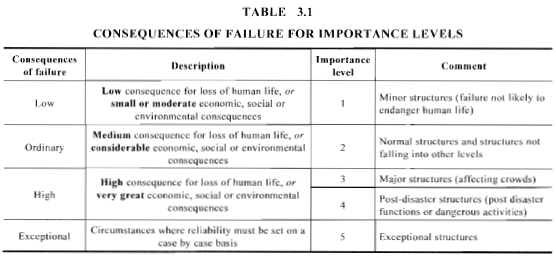
Figura 6. Definición del nivel de importancia según la tabla 3.1 de AS / NZS 1170.0.
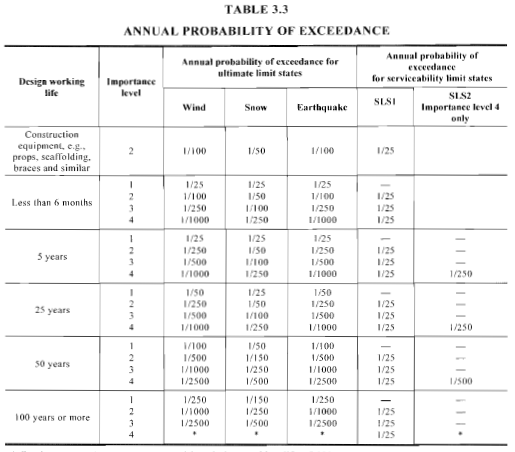
Figura 7. Definición de probabilidad anual de excedencia según la tabla 3.3 de AS / NZS 1170.0.
Para nuestro ejemplo, solo consideraremos el estado límite final. Nuestra estructura de ejemplo se clasifica en “Ordinario” y se supone que tiene una vida laboral de diseño de 50 años. Por lo tanto, adoptaremos la probabilidad anual de excedencia equivalente a 1/500. Por lo tanto, el valor correspondiente de nuestro \({V }_ _{R}\) es 45 em.
SkyCiv ahora automatiza la detección de la región del viento y obtiene el valor de la velocidad del viento correspondiente con solo unas pocas entradas. Prueba nuestra herramienta gratuita de viento de SkyCiv
Multiplicador de dirección del viento, \({M}_ _{d}\)
Para cada región del viento y la dirección correspondiente del viento. (8 direcciones cardinales), multiplicador de dirección del viento, \({M}_ _{d}\), son diferentes en valores como se muestra en la Tabla 3.2 de AS / NZS 1170.2.
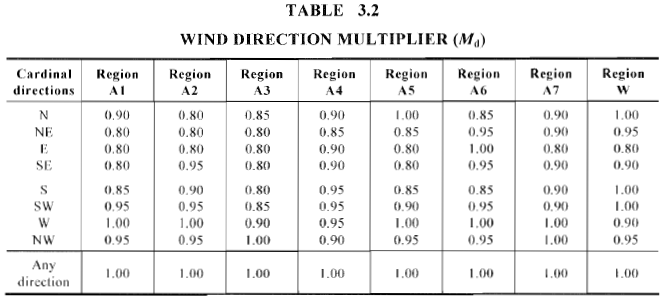
Figura 8. Valores multiplicadores de dirección del viento por región y dirección del viento según la tabla 3.2 de AS / NZS 1170.2.
En este ejemplo, comprobaremos la velocidad del viento procedente de “NACIDO” en el cual \({M}_ _{d}\) = 0.85. sin embargo, también es seguro asumir \({M}_ _{d}\) = 1.0 para dar un resultado conservador.
Multiplicador de terreno / altura, \({M}_ _{z,gato}\)
Para calcular el terreno / multiplicador de altura \({M}_ _{z,gato}\), necesitamos clasificar la categoría de terreno de nuestro sitio. Tabla 2 muestra la definición de cada categoría de terreno basada en la Sección 4.2.1 de AS / NZS 1170.2. \({M}_ _{z,gato}\) ahora se puede calcular usando la tabla 4.1 de AS / NZS 1170.2 dependiendo de la altura, región del viento y categoría de terreno de la estructura.
Tabla 2. Definición de categoría de terreno para AS / NZS 1170.2.
| Categoría de terreno | Definición |
|---|---|
| Categoría 1 | Terreno abierto expuesto con pocas o ninguna obstrucción y superficies de agua a velocidades de viento de servicio |
| Categoría 2 | Superficies de agua, terreno abierto, pastizales con pocos, obstrucciones bien dispersas que tienen alturas generalmente de 1.5 ma 10 m |
| Categoría 3 | Terreno con numerosas obstrucciones espaciadas 3 m a 5 m de altura, tales como áreas de viviendas suburbanas. |
| Categoría 4 | Terreno con numerosos grandes, alto (10 m a 30 m de altura) y obstrucciones muy espaciadas, tales como grandes centros urbanos y complejos industriales bien desarrollados. |
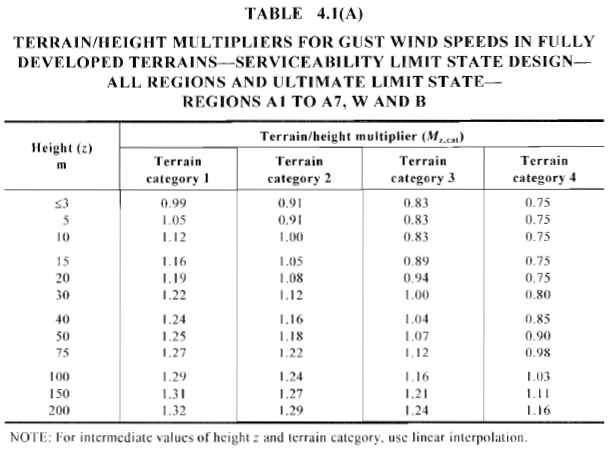
Figura 9. Multiplicador calculado de terreno / altura, \({M}_ _{z,gato}\) , basado en la categoría de terreno correspondiente y la región del viento (Tabla 4.1 de AS / NZS 1170.2).
Para nuestro ejemplo, la ubicación del sitio se puede clasificar como “Categoría 2” asumiendo que tenemos una categoría de terreno uniforme para cada dirección del viento. Dividiremos la altura de la estructura por cada 3 my la altura media del techo. Los valores tabulados de \({M}_ _{z,gato}\) para cada nivel se muestra en la Tabla 3.
Tabla 3. Calculado \({M}_ _{z,gato}\) para cada nivel de la estructura.
| Altura, m | \({M}_ _{z,gato}\) |
|---|---|
| 3 m | 0.91 |
| 6 m | 0.928 |
| 9 m | 0.982 |
| 10.06 m | 1.001 |
Multiplicador de blindaje, \({M}_ _{s}\)
El efecto de blindaje se puede considerar al calcular las presiones de viento de diseño usando AS / NZS 1170.2. Esto es para considerar la disminución de la presión del viento cuando existen estructuras cercanas. Sección de 4.3 de AS / NZS 1170.2 detalla el cálculo del factor de blindaje \({M}_ _{s}\). En este ejemplo, ya que la ubicación del sitio está situada en un campo abierto, y estructuras cercanas tienen una distancia mayor a 20h (201.2 m) de la estructura, podemos asumir el \({M}_ _{s}\) = 1.0.
Multiplicador topográfico, \({M}_ _{t}\)
El efecto de la topografía sobre la presión del viento se captura en el multiplicador topográfico., \({M}_ _{t}\), donde amplifica la presión del viento de diseño en función de la elevación del terreno del sitio, si la estructura está en una colina o escarpa. Sección de 4.4 de la AS / NZS 1170.2 detalla el cálculo de este parámetro. Fuera de la zona topográfica local., una distancia calculada desde el pico de la colina o escarpa, la \({M}_ _{t}\) puede considerarse igual a 1.0 como se muestra en las figuras 4.2 y 4.3 de AS / NZS 1170.2 (Figura 10).
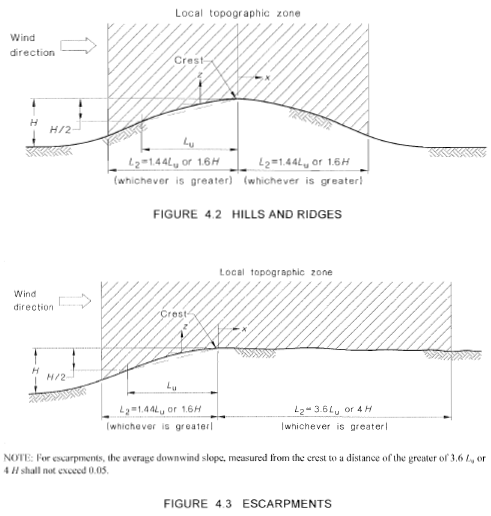
Figura 10. Parámetros necesarios para calcular el factor topográfico, \({M}_ _{t}\) , basado en la sección 4.4 de AS / NZS 1170.2.
De los datos de elevación del terreno del sitio (de Google Maps, viniendo de NE), deducimos que la topografía se puede clasificar como colina. Con base en la Figura 4.2 de AS / NZS 1170.2, Los siguientes puntos se pueden obtener como se muestra en la Tabla 4:
Tabla 4. Puntos de datos extraídos de datos de elevación del suelo (de Google Maps) como se muestra en la figura 11.
| Parámetro | Valor |
| Mt | 1.076 |
| Pendiente | 0.07 |
| Ubicación del pico | -380.00 m de la ubicación de la estructura |
| Elevación de pico | 628.16 m |
| Ubicación del pie | -2000.00 m de la ubicación de la estructura |
| Elevación del pie | 515.37 m |
| H | 112.79 m |
| Sitio. de H / 2 | -1154.23 m de la ubicación de la estructura |
| x | 380.00 m |
| Ltu | 774.23 m |
| L1 | 278.72 m |
| L2 | 1114.89 m |
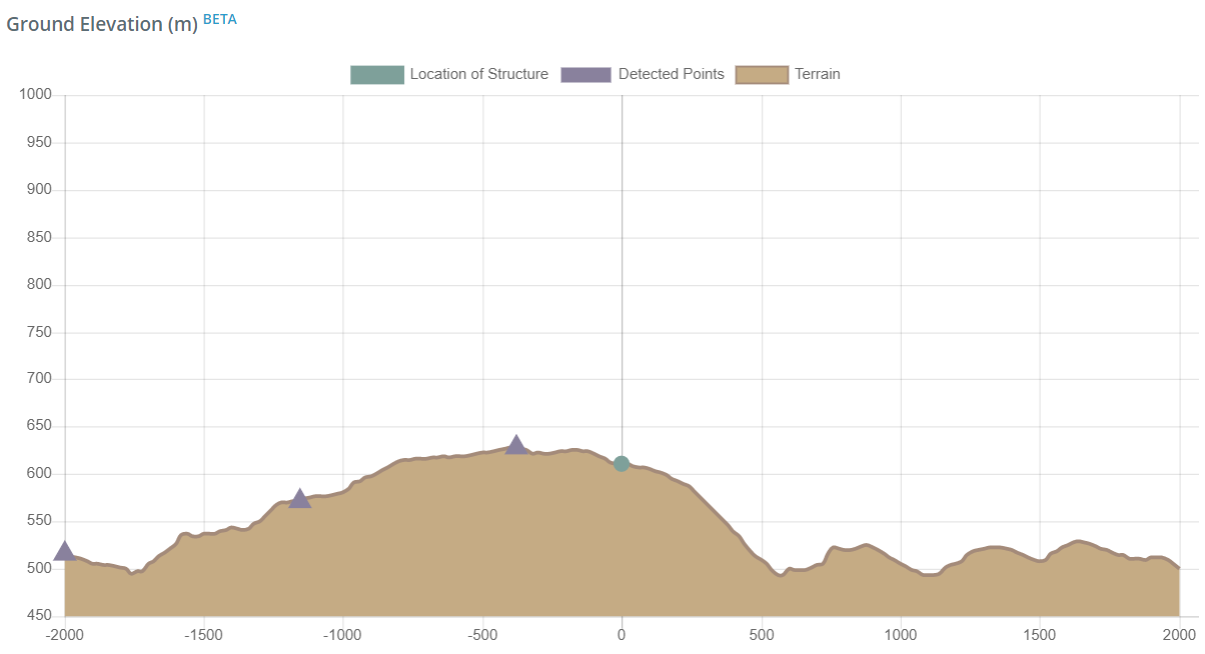
Figura 11. Elevación del terreno del sitio en la sección NE-SW (de Google Maps).
De los datos mostrados en la tabla 4, el multiplicador topográfico calculado, \({M}_ _{t}\), es igual a 1.08 basado en la ecuación 4.4(2) de AS / NZS 1170.2 como se muestra en la ecuación (5).
\({M}_ _{t} = {M}_ _{h} = 1 + [ H / 3.5(z + {L}_ _{1})] [ 1 – ( |x| / {L}_ _{2})] \) (5)
\({M}_ _{t} = 1.08 \)
Finalmente, usando la ecuación (1), la velocidad calculada del viento de diseño se muestra en la Tabla 5.
Tabla 5. Calculado \({V }_ _{sentar,si}\) para cada nivel de la estructura.
| Altura, m | \({V }_ _{sentar,si}\), em |
| 3 | 37.45 |
| 6 | 38.19 |
| 9 | 40.42 |
| 10.06 | 41.20 |
Dónde:
\({V }_ _{sentar,si (mínimo)}\) = 30 m/s para estructuras permanentes.
Para calcular las presiones de viento de diseño, los factores de forma aerodinámica, \({C}_ _{higo}\), para superficies internas y externas son necesarias. Esto se discutirá en la siguiente sección.
Factor de forma aerodinámica, \({C}_ _{higo}\)
El factor de forma aerodinámica., \({C}_ _{higo}\), se utiliza para determinar los valores de presión del viento aplicados a cada superficie. Un valor positivo de \({C}_ _{higo}\) significa que la presión está actuando hacia la superficie, mientras que negativa significa actuar lejos de la superficie.
Factor de forma aerodinámica para presión interna, \({C}_ _{higo,i}\)
Coeficiente de presión interna, \({C}_ _{pag,i}\)
Por \({C}_ _{higo,i}\), el cálculo del coeficiente de presión interna \({C}_ _{pag,i}\) se detalla en la tabla 5.1 de AS / NZS 1170.2 como se muestra en la figura 12.
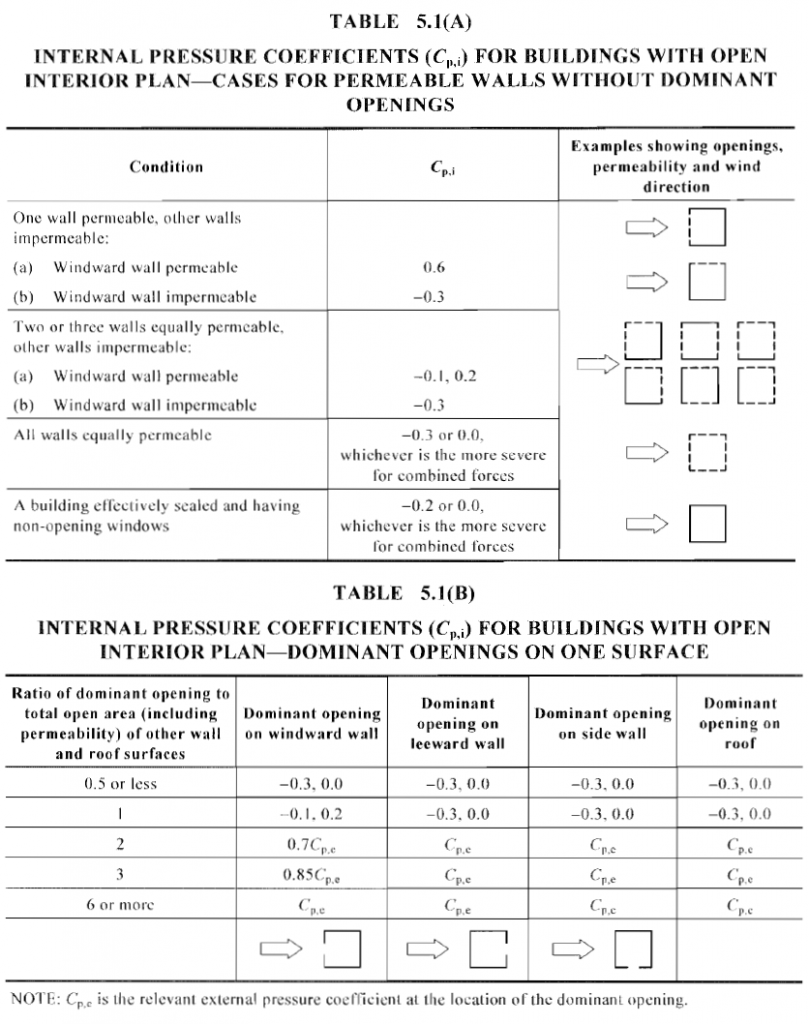
Figura 12. Coeficiente de presión interna, \({C}_ _{pag,i}\), como se define en la Sección 5.3 de AS / NZS 1170.2.
En este ejemplo, nuestra estructura está cerrada y se supone que no tiene apertura, por lo tanto, la condición apropiada para esto es la estructura es “Un edificio efectivamente escalado y con ventanas que no se abren” y los correspondientes coeficientes de presión interna son \({C}_ _{pag,i}\) = -0.2, 0.0.
Factor de forma aerodinámica para presión externa, \({C}_ _{higo,mi}\)
Coeficiente de presión externa, \({C}_ _{pag,mi}\)
Sección de 5.4 de AS / NZS 1170.2 define el procedimiento para obtener el coeficiente de presión externa, \({C}_ _{pag,mi}\), para edificios rectangulares. Las superficies de construcción para la distribución de presión externa se definen en la Figura 5.2 del código como se muestra si la Figura 13. Además, Mesas 5.2 a 5.3 de AS / NZS 1170.2 detalla los valores calculados de \({C}_ _{pag,mi}\) para cada definición de superficie como se muestra en las Figuras 14 a 18.
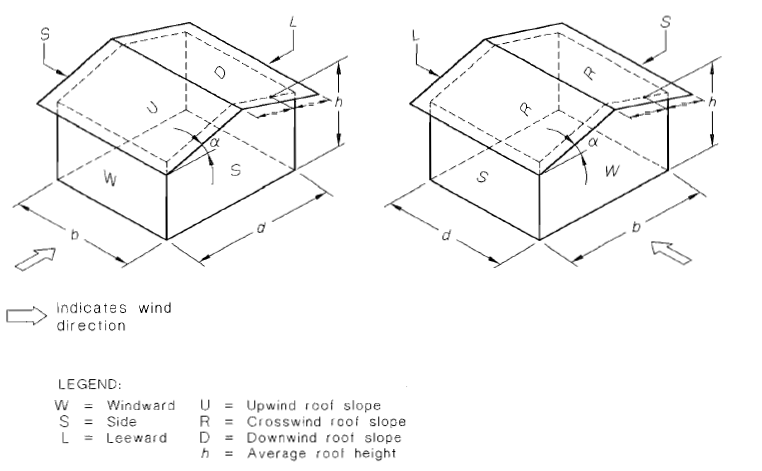
Figura 13. Definición de superficie para distribución de presión externa, como se define en la Sección 5.4 de AS / NZS 1170.2.
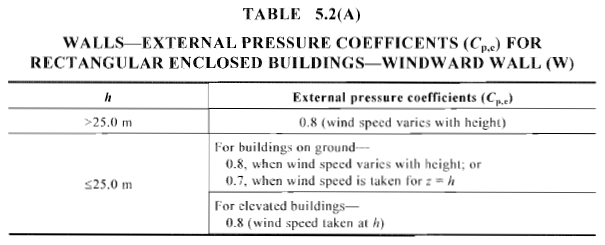
Figura 14. Coeficiente de presión externa calculada, \({C}_ _{pag,mi}\), para barlovento de edificios rectangulares cerrados (Tabla 5.2(A) de AS / NZS 1170.2).
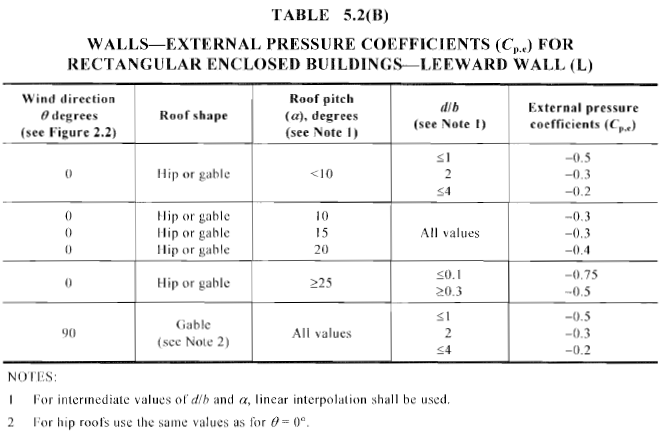
Figura 15. Coeficiente de presión externa calculada, \({C}_ _{pag,mi}\), para muro de sotavento de edificios cerrados rectangulares (Tabla 5.2(B) de AS / NZS 1170.2).
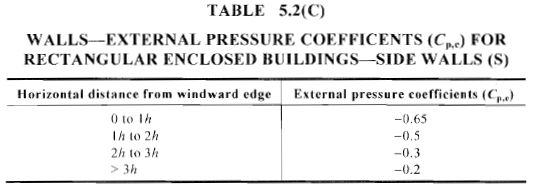
Figura 16. Coeficiente de presión externa calculada, \({C}_ _{pag,mi}\), para paredes laterales de edificios rectangulares cerrados (Tabla 5.2(C) de AS / NZS 1170.2).
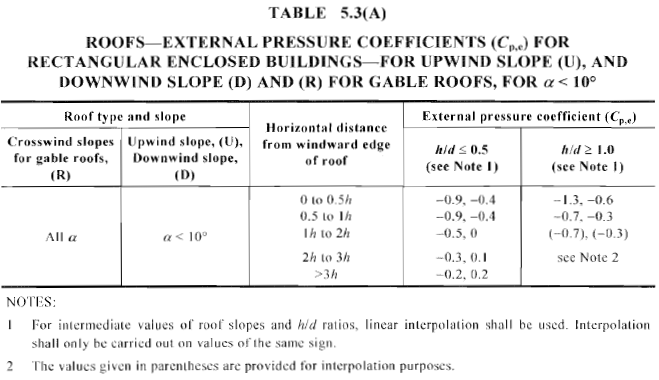
Figura 17. Coeficiente de presión externa calculada, \({C}_ _{pag,mi}\), Para la superficie del techo a dos aguas a favor y en contra del viento con ángulo de inclinación < 10° (Tabla 5.3(A) de AS / NZS 1170.2).
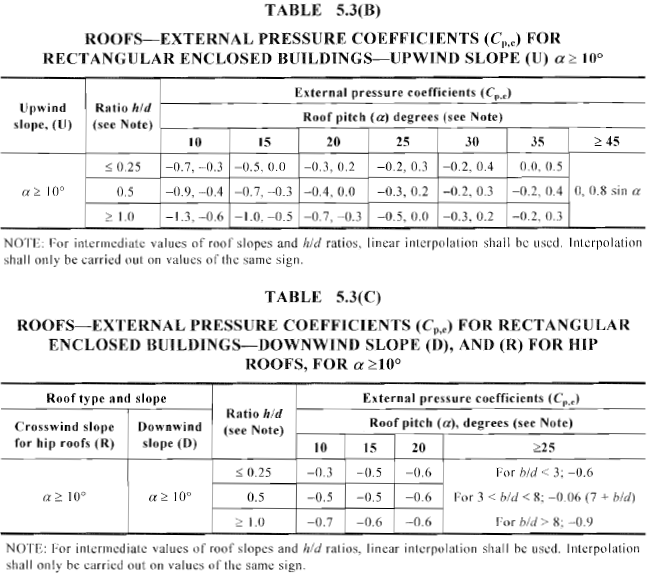
Figura 18. Coeficiente de presión externa calculada, \({C}_ _{pag,mi}\), para la superficie del aguilón y el techo de la cadera con viento a favor y en contra del viento con ángulo de inclinación ≥ 10° (Tabla 5.3(A) y mesa 5.3(B) de AS / NZS 1170.2).
En este ejemplo, \({C}_ _{pag,mi}\) los valores para las superficies de las paredes se muestran en la Tabla 6 y 7 debajo de donde \(d/b) = 0.616 para 0° y \(b / d ) = 1.625 para 90° , \(h / d ) = 0.516, y \(h/b\) = 0.317 . Además, Tabla 8 muestra el \({C}_ _{pag,mi}\) valores para superficies de techo.
Tabla 6. Coeficientes de presión externa calculados, \({C}_ _{pag,mi}\), para superficies de paredes de barlovento y sotavento.
| Altura, m | \({C}_ _{pag,mi}\) (barlovento) | \({C}_ _{pag,mi}\) (sotavento) - a lo largo de L (0°) |
\({C}_ _{pag,mi}\) (sotavento) - a lo largo de B (90°) |
| 3 | 0.8 | -0.3 | -0.375 |
| 6 | 0.8 | ||
| 9 | 0.8 | ||
| 10.06 | 0.7 |
Tabla 7. Coeficientes de presión externa calculados, \({C}_ _{pag,mi}\), para superficies laterales.
| Ubicación desde el muro de barlovento, m | \({C}_ _{pag,mi}\) (pared lateral) |
| 0 a 10.06m | -0.65 |
| 10.06 a 19.507 m | -0.50 |
Tabla 8. Coeficientes de presión externa calculados, \({C}_ _{pag,mi}\), para superficies de techo.
| Superficie del techo | \({C}_ _{pag,mi}\) |
| Contra el viento | -0.888, -0.394 |
| Viento abajo | -0.503 |
| Viento de costado | -0.9, -0.4 (0 a h) -0.5, 0.0 (ha 2 h) -0.3, 0.1 (2ha 3 h) -0.2, 0.2 (> 3h) |
Factor de reducción de área, \({K}_ _{a}\)
Factor de reducción de área, \({K}_ _{a}\), solo es aplicable a paredes laterales y superficies de techo. De lo contrario calculado, \({K}_ _{a}\) siempre es igual a 1.0. Tabla 5.4 de AS / NZS 1170.2 muestra el valor de \({K}_ _{a}\) dependiendo del área contribuyente para las paredes laterales y las superficies del techo como se muestra en la Figura 19.

Figura 19. Valores del factor de reducción de área, \({K}_ _{a}\), para paredes laterales y superficies de techo (Tabla 5.4 de AS / NZS 1170.2).
Para nuestro ejemplo, los valores calculados del factor de reducción de área se muestran en la Tabla 9 a continuación.
Tabla 9. Valores del factor de reducción de área, \({K}_ _{a}\), para este ejemplo.
| Superficie | Area, m2. | \({K}_ _{a}\) |
| pared lateral (a lo largo de d) | 196.21 | 0.8 |
| pared lateral (a lo largo de b) | 285.29 | 0.8 |
| techo – barlovento | 314.564 | 0.8 |
| techo – sotavento | 314.564 | 0.8 |
| techo – viento de costado | 629.129 | 0.8 |
Factor de presión local para revestimientos, \({K}_ _{l}\)
El factor de presión local, \({K}_ _{l}\), siempre es igual a 1.0 a todas las superficies excepto los componentes y revestimientos. Sección de 5.4.4 de AS / NZS 1170.2 detalla el procedimiento de cálculo para obtener \({K}_ _{l}\) para estos componentes.
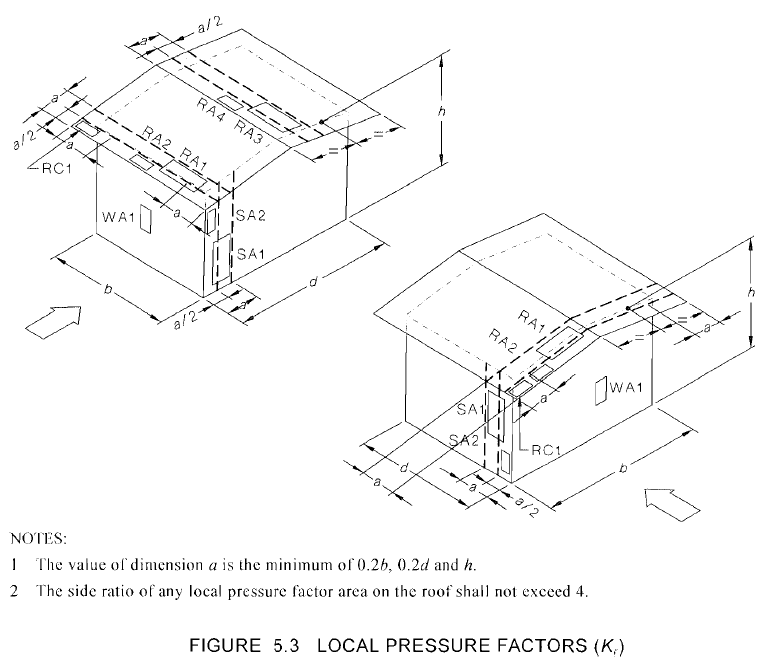
Figura 20. Ubicación de las presiones de revestimiento como se define en la Tabla 5.6 de AS / NZS 1170.2.
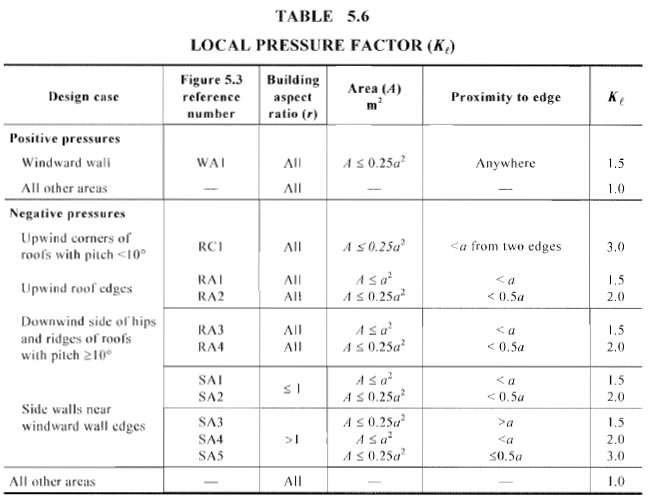
Figura 21. Valores del factor de presión local., \({K}_ _{l}\), para cada zona como se muestra en la Figura 20.
En este ejemplo, los valores de \(una) es el mínimo de \(0.2b\) (3.91 m), \(02.d\) (6.34 m), o \(h ) (10.06m), por lo tanto, \(una) = 3.91 m. El área correspondiente y el factor de presión local para correas y montantes de pared se muestran en la Tabla 10 a continuación con la suposición de que la longitud del tramo de la correa es igual al espacio de las armaduras (7.924 m) y la longitud del tramo de los montantes de la pared es igual a la altura de la historia (3 m). La relación de aspecto del edificio es la más grande de \(h / d ) (0.516) y \(h/b\) (0.317).
Tabla 10. Valores del factor de presión local. \({K}_ _{l}\) para correas y montantes de pared.
| Revestimiento | Area, m2. | Zonas | Kl para presión positiva | Kl para presión negativa |
| correa | 4.75 | RA1 | 1.0 | 1.5 |
| RA3 | 1.0 | 1.5 | ||
| postes de pared | 1.80 | WA1 | 1.0 | 1.0 |
| SA1 | 1.0 | 1.5 | ||
| SA2 | 1.0 | 2.0 |
Factor de reducción de revestimiento permeable, \({K}_ _{pag}\), para tejados y paredes laterales
El factor de reducción de revestimiento permeable, \({K}_ _{pag}\), siempre es igual a 1.0 a todas las superficies, excepto que una superficie externa consiste en revestimiento permeable y la relación de solidez es menor que 0.999 donde la relación de solidez es la relación del área sólida al área de superficie total. En este ejemplo, asumiremos que \({K}_ _{pag}\) es igual a 1.0.
Factores de combinación de acción, \({K}_ _{c,i}\) y \({K}_ _{c,mi}\)
Factores de combinación de acción, \({K}_ _{c,i}\) y \({K}_ _{c,mi}\), se utilizan para calcular el efecto de la carga del viento que actúa simultáneamente sobre superficies específicas (como el viento que actúa sobre las paredes, cubiertas, y presiones internas). Tabla 5.5 de la AS / NZS 1170.2 muestra ejemplos de combinación de acción con sus factores de combinación de acción correspondientes como se ilustra en la Figura 22.
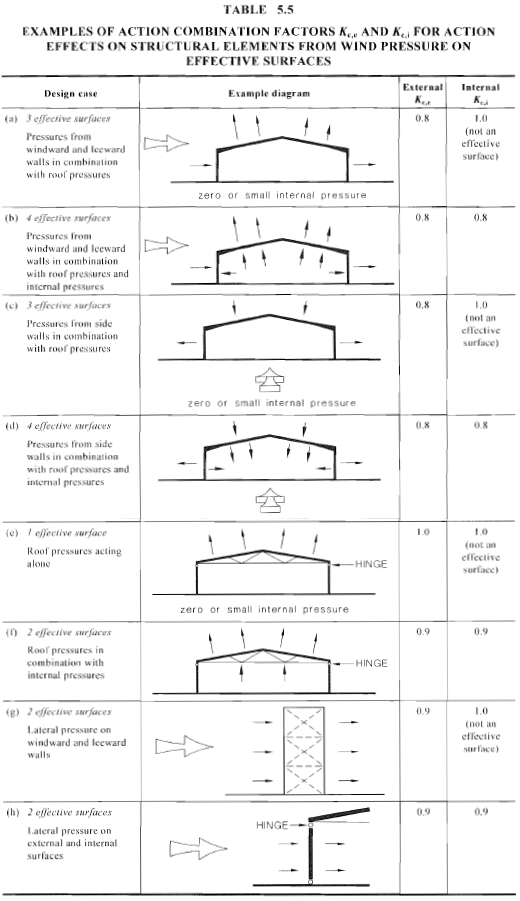
Figura 22. Factores de combinación de acción \({K}_ _{c,mi}\) y \({K}_ _{c,i}\) de la mesa 5.5 de AS / NZS 1170.2.
En este ejemplo, consideraremos caso de diseño (b) dónde 4 las superficies efectivas están cargadas de presiones de diseño. Por lo tanto, \({K}_ _{c,i}\) y \({K}_ _{c,mi}\) son ambos iguales a 0.8.
Diseño de presiones de viento para el bastidor principal
Ya tenemos los parámetros necesarios., \(pags), podemos obtener los valores de diseño de la presión del viento usando Ecuaciones (2) a (4). Mesas 11 a 13 muestra el resumen de parámetros para cada superficie.
Tabla 11. Valores de presión de diseño para muro de barlovento.
| la altura, m | \({M}_ _{z,gato}\) | \({V }_ _{desde,θ}\) | \({C}_ _{higo}\) | \({C}_ _{pag,mi}\) | \({K}_ _{a}\) | \({K}_ _{c,mi}\) | \({K}_ _{l}\) | \({K}_ _{pag}\) | Presión de diseño \(pags), Bien |
| 3 | 0.910 | 37.45 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 538.64 |
| 6 | 0.928 | 38.19 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 560.16 |
| 9 | 0.982 | 40.42 | 0.640 | 0.8 | 1 | 0.8 | 1 | 1 | 627.25 |
| 10.06 | 1.001 | 41.20 | 0.560 | 0.7 | 1 | 0.8 | 1 | 1 | 570.29 |
Tabla 12. Valores de presión de diseño calculados para sotavento y paredes laterales, y superficies de techo.
| Superficie | \({V }_ _{desde,θ}\) | \({C}_ _{higo}\) | \({C}_ _{pag,mi}\) | \({K}_ _{a}\) | \({K}_ _{c,mi}\) | \({K}_ _{l}\) | \({K}_ _{pag}\) | Presión de diseño \(pags), Bien |
| Muro de sotavento | 41.20 | -0.24 | -0.3 | 1 | 0.8 | 1 | 1 | -244.41 |
| Pared lateral (0 a 10.06m) |
-0.520* | -0.65 | 0.8 | 0.8 | 1 | 1 | -529.55 | |
| Pared lateral (0 a 10.06m) |
-0.400* | -0.5 | 0.8 | 0.8 | 1 | 1 | -407.35 | |
| Techo (contra el viento) |
-0.710* | -0.888 | 0.80 | 0.8 | 1.0 | 1.0 | -723.13 | |
| -0.315* | -0.394 | 0.80 | 0.8 | 1.0 | 1.0 | -320.99 | ||
| Techo (viento abajo) |
-0.402* | -0.503 | 0.80 | 0.8 | 1.0 | 1.0 | -409.79 | |
| Techo (viento de costado) |
-0.720* -0.400* -0.240* -0.160* |
-0.90 -0.50 -0.30 -0.20 |
0.80 0.80 0.80 0.80 |
0.8 0.8 0.8 0.8 |
1.0 1.0 1.0 1.0 |
1.0 1.0 1.0 1.0 |
-733.23 (0 a h) -407.35 (ha 2 h) -244.41 (2ha 3 h) -162.94 (> 3h) |
Tabla 13. Presiones internas calculadas del viento que actúan simultáneamente con presiones externas.
* – producto de \({K}_ _{a}\) y \({K}_ _{c,mi}\) no será inferior a 0.8 (Sección de 5.4.3 de AS / NZS 1170.2).
| Superficie | \({V }_ _{desde,θ}\) | \({C}_ _{higo,i}\) | \({C}_ _{pag,i}\) | \({K}_ _{c,i}\) | Presión de diseño \(pags), Bien |
| Presión interna | 41.20 | 0.0 | 0.0 | 0.8 | 0.0 |
| 41.20 | -0.16 | -0.2 | 0.8 | -162.94 |
Para resumir el diseño, las presiones se muestran en la Tabla 14 y 15 combinando el efecto de la acción de presión externa e interna.
Tabla 14. Diseño calculado de presiones de viento para muro de barlovento.
| la altura, m | Presión externa \({pag}_ _{mi}\), Bien | Presión interna, Bien | Presión combinada, Bien | ||
| \({pag}_ _{i,max}\) | \({pag}_ _{i,min}\) | \({pag}_ _{mi}-{pag}_ _{i,max}\) | \({pag}_ _{mi}-{pag}_ _{i,min}\) | ||
| 3 | 538.64 | 0.00 | -162.94 | 538.64 | 701.58 |
| 6 | 560.16 | 0.00 | -162.94 | 560.16 | 723.10 |
| 9 | 627.25 | 0.00 | -162.94 | 627.25 | 790.19 |
| 10.06 | 570.29 | 0.00 | -162.94 | 570.29 | 733.23 |
Tabla 15. Diseño calculado de presiones de viento para otras superficies.
| Superficie | Presión externa \({pag}_ _{mi}\), Bien | Presión interna, Bien | Presión combinada, Bien | ||
| \({pag}_ _{i,max}\) | \({pag}_ _{i,min}\) | \({pag}_ _{mi}-{pag}_ _{i,max}\) | \({pag}_ _{mi}-{pag}_ _{i,min}\) | ||
| Muro de sotavento | -244.41 | 0.00 | -162.94 | -244.41 | -81.47 |
| Pared lateral (0 a 10.06m) | -529.55 | 0.00 | -162.94 | -529.55 | -366.61 |
| Pared lateral (10.06 a 19.507m) | -407.35 | 0.00 | -162.94 | -407.35 | -244.41 |
| Techo (contra el viento) | -723.13 | 0.00 | -162.94 | -723.13 | -560.19 |
| -320.99 | 0.00 | -162.94 | -320.99 | -158.05 | |
| Techo (viento abajo) | -409.79 | 0.00 | -162.94 | -409.79 | -246.85 |
| Techo (viento de costado) | -733.23 (0 a h) -407.35 (ha 2 h) -244.41 (2ha 3 h) -162.94 (> 3h) |
0.00 | -162.94 | -733.23 (0 a h) -407.35 (ha 2 h) -244.41 (2ha 3 h) -162.94 (> 3h) |
-570.29 (0 a h) -244.41 (ha 2 h) -81.47 (2ha 3 h) 0 (> 3h) |
Dado que el espacio de cada cuadro es igual a 7.925 m, considerando un cuadro, Las cargas de viento distribuidas equivalentes que actúan sobre el marco se muestran en las Figuras. 23 y 24. Tenga en cuenta que tendremos dos casos de carga para ser considerados, y los valores absolutos máximos de la presión del viento del techo se tienen en cuenta para cada caso.
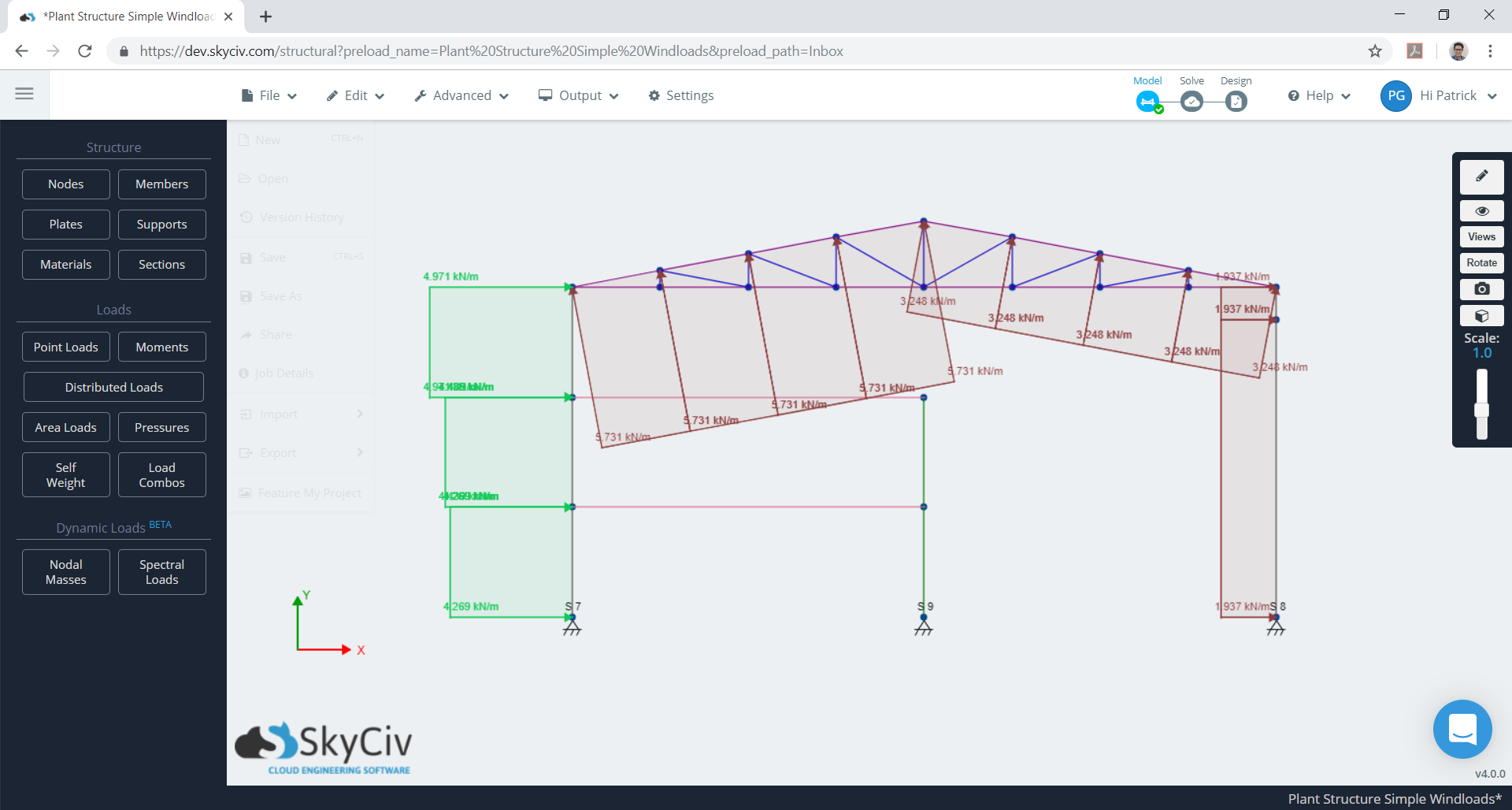
Figura 23. Presiones de viento de diseño equivalente para un cuadro (caso 1).
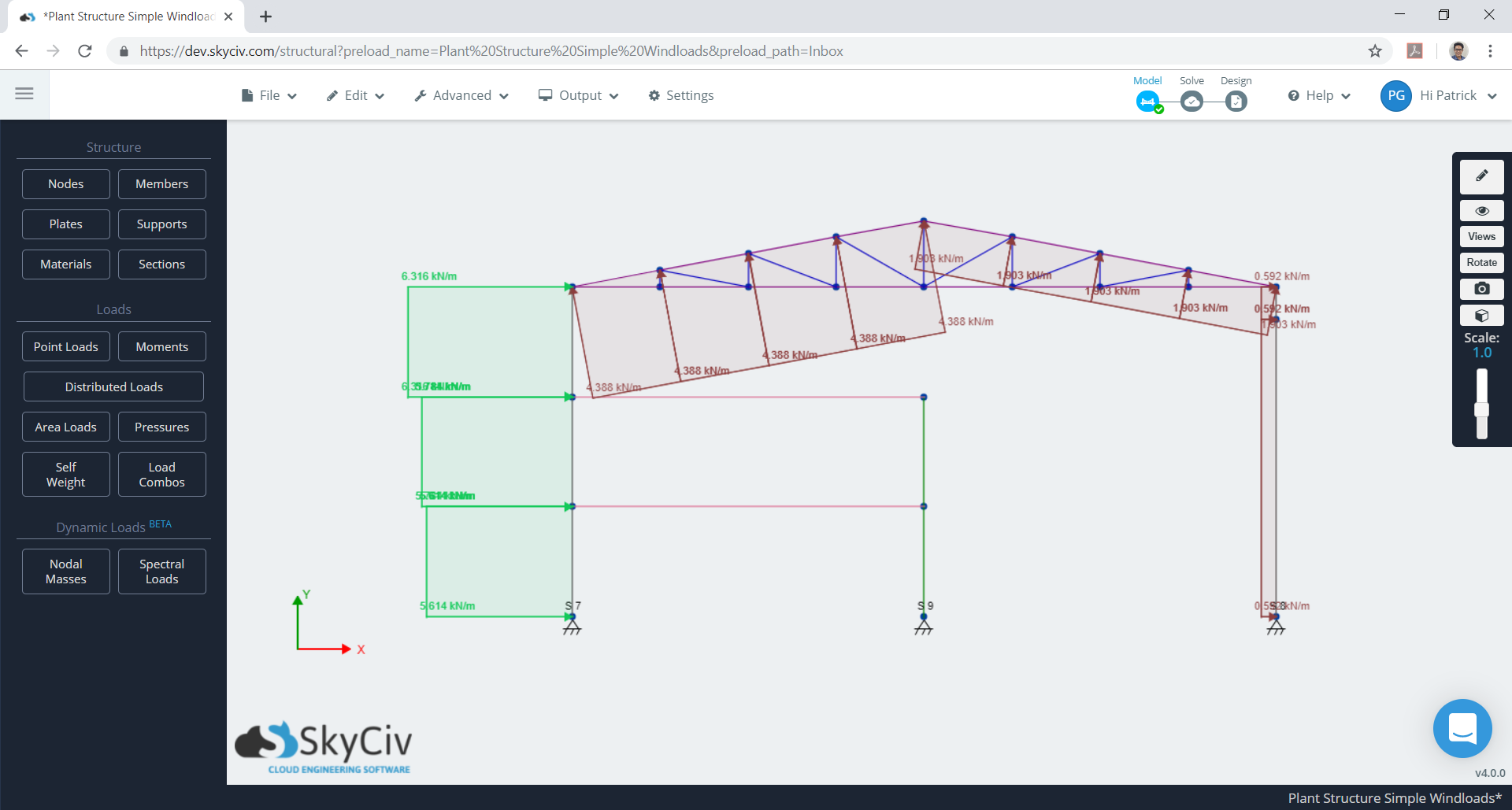
Figura 24. Presiones de viento de diseño equivalente para un cuadro (caso 2).
Todos estos cálculos pueden realizarse utilizando el Software de carga de viento de SkyCiv para ASCE 7-10, 7-16, EN 1991, NBBC 2015, AS 4055 y AS 1170. Los usuarios pueden ingresar la ubicación del sitio para obtener las velocidades del viento y los factores topográficos, ingresar los parámetros del edificio y generar las presiones de viento. Con una cuenta profesional, los usuarios pueden aplicar esto automáticamente a un modelo estructural y ejecutar análisis estructurales en un solo software.
De lo contrario, tratar nuestra herramienta gratuita de viento de SkyCivo reservar PRUEBA GRATIS para obtener asistencia con sus proyectos de ingeniería para usuarios existentes
Ingeniero estructural, Desarrollo de Producto
Maestría en Ingeniería Civil
Referencias:
- Comité Técnico Conjunto. (2011). AS / NZS 1170.2: 2011 Acciones de diseño estructural-Parte 2: Acciones de viento. Estándar australiano / neozelandés (AS / NZS), Comité Técnico Conjunto BD-006, Australia / Nueva Zelanda.



