Ejemplo de cálculo del momento de vuelco – Ejemplo de cálculo del momento de vuelco

Esta es una guía simple sobre cómo calcular el momento de volteo en un muro de contención con ejemplos. Ejemplo de cálculo del momento de vuelco. Ejemplo de cálculo del momento de vuelco. Ejemplo de cálculo del momento de vuelco (Ejemplo de cálculo del momento de vuelco) Ejemplo de cálculo del momento de vuelco:

Ejemplo de cálculo del momento de vuelco:

• Ejemplo de cálculo del momento de vuelco
• Ejemplo de cálculo del momento de vuelco
• Ejemplo de cálculo del momento de vuelco

Ejemplo de cálculo del momento de vuelco:

• Ejemplo de cálculo del momento de vuelco
• Ejemplo de cálculo del momento de vuelco

Eso dicho, Ejemplo de cálculo del momento de vuelco:

Ejemplo de cálculo del momento de vuelco:

Ejemplo de cálculo del momento de vuelco

• Altura: 3.124 m
• Anchura: 0.305 m
• Compensar: 0.686 m

Base

• Anchura: 2.210 m
• Grosor: 0.381 m

Ejemplo de cálculo del momento de vuelco

• Ejemplo de cálculo del momento de vuelco: 18.85 kN / m³
• Ángulo de fricción: 35 grados

Subestructura Suelo

• Ejemplo de cálculo del momento de vuelco: 18.85 kN / m³
• Ángulo de fricción: 35 grados
• Coeficiente de fricción suelo-concreto: 0.55
• Presión de rodamiento admisible: 143.641 kPa

capas de suelo:

• Activo: 3.505 m
• Pasivo: 0.975 m
• Infraestructura: 0.792 m

Valor de carga de recargo: -17.237 kN / m

Cargas verticales:

Todas las cargas verticales a las que está sometido el muro de contención en voladizo de hormigón se muestran en la siguiente figura:

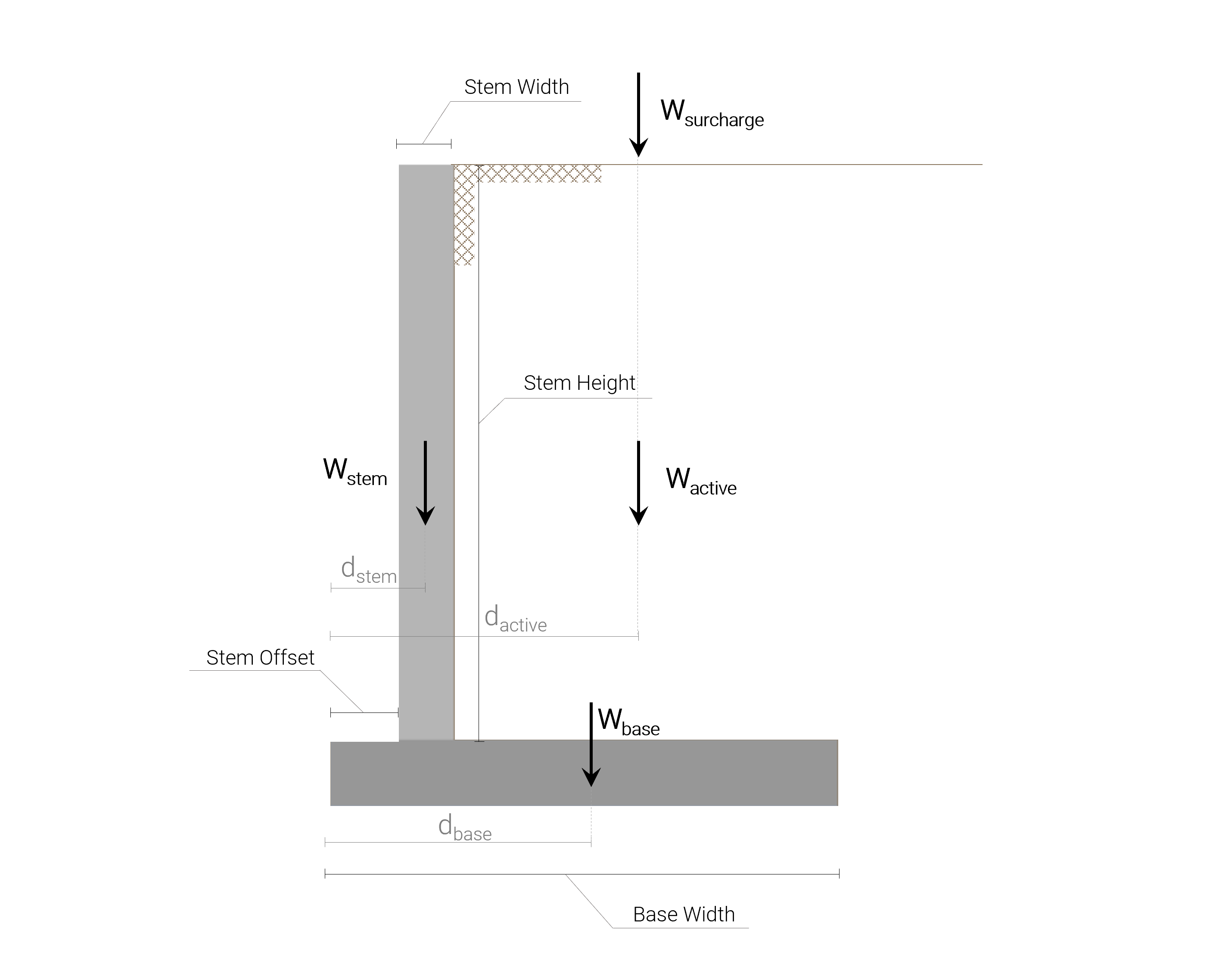
Vale la pena mencionar aquí, que el peso (carga vertical) y el momento asociado con la porción de suelo pasivo se desprecian ya que podría ser removido o erosionado y es una suposición conservadora.

\(W_{madre} = gamma_{hormigón} \cdot (madre_{la altura} \tallo cdot_{anchura} ) = 23.58 \;kN/m^3 cdot 3.124\;m cdot 0.305\;metro)

\( W_{madre}= 22.467\;kN/m)

\(W_{base} = gamma_{hormigón} \cdot (base_{grosor} \cdot base_{anchura} ) = 23.58 \;kN/m^3 cdot 0.381\;m cdot 2.210\;metro)

\( W_{base}= 18.855\;kN/m)

\(W_{activo} = gamma_{suelo,\;activo} \cdot (madre_{la altura}\cdot (base_{anchura}-madre_{compensar}-madre_{anchura}) ) \)

\( W_{activo} = 18.85 \;kN/m^3 cdot 3.124\;m cdot (2.210-0.686-0.305)\;metro)

\( W_{activo} = 71.784\;kN/m)

\(W_{recargo} = recargo_{valor} \cdot ( (base_{anchura}-madre_{compensar}-madre_{anchura} ) \)

\( W_{recargo} = 17.237 \;kN/m \cdot (2.210-0.686-0.305)\;metro)

\( W_{recargo} = 21.012\;kN/m)

 

Calculadora de Muros de Contención

Momento restaurador:

El momento restaurador es el encargado de evitar que la pared gire con respecto a la esquina más inferior izquierda de la base.. Para calcularlo, se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales:

\(METRO_{madre}se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{madre}\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{madre} = 22.467\;kN/m cdot 0.839\;m=18.839;kNm/m\)

\(METRO_{base}se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{base}\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{base} = 18.855\;kN/m cdot 1.105\;m=21.939\;kNm/m\)

\(METRO_{activo}se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo}\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo} = 71.784\;kN/m cdot 1.601\;m=114.89\;kNm/m\)

\(METRO_{recargo}se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo}\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} = 21.012\;kN/m cdot 1.601\;m=33.630\;kNm/m\)

\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{R}} se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{madre}+METRO_{base}+METRO_{activo}+METRO_{recargo}\)

\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{R}} = 18.839+21.939+114.89+33.630\)

\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{R}} = 189.298\;kNm/m\)

se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales:

se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales:

se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales, se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales:

\( K_a = frac{1-\sin(\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{suelo,\;activo})}{1+\sin(\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{suelo,\;activo})} \)

\( K_a = frac{1-\sin(35º)}{1+\sin(35º)} = 0.271 \)

se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales, se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales:

\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo} = frac{1}{2} \cdotgamma_{suelo,\;activo} \cdot (madre_{la altura} + base_{grosor})^{2} \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales \)

\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo} = frac{1}{2} \cdot 18.85\;kN/m^3 cdot 3,505^{2} \cdot 0.271 \)

\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo} = 31.377\;kN / m \)

Para el cálculo de la fuerza horizontal relacionada con la presencia de sobrecarga, primero se calcula una altura equivalente del suelo, y luego la fuerza real:

\( h_{suelo,\;equivalente} = frac{recargo_{valor}}{\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{suelo,\;activo}} = frac{17.237 \;= gamma_{2}}{18.85 \;= gamma_{3}} \)

\( h_{suelo,\;equivalente} = 0.914 \; m \)

\( se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} = \gamma_{suelo,\;activo} \cdot h_{suelo,\;equivalente} \cdot (madre_{la altura} + base_{grosor}) \cdot K_a\)

\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} =\cdot 18.85\;kN/m^3 cdot 0.914 \; m cdot 3.505 \; m cdot 0.271 \)

\(se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{recargo} = 16.372\;kN / m \)

Momento de vuelco

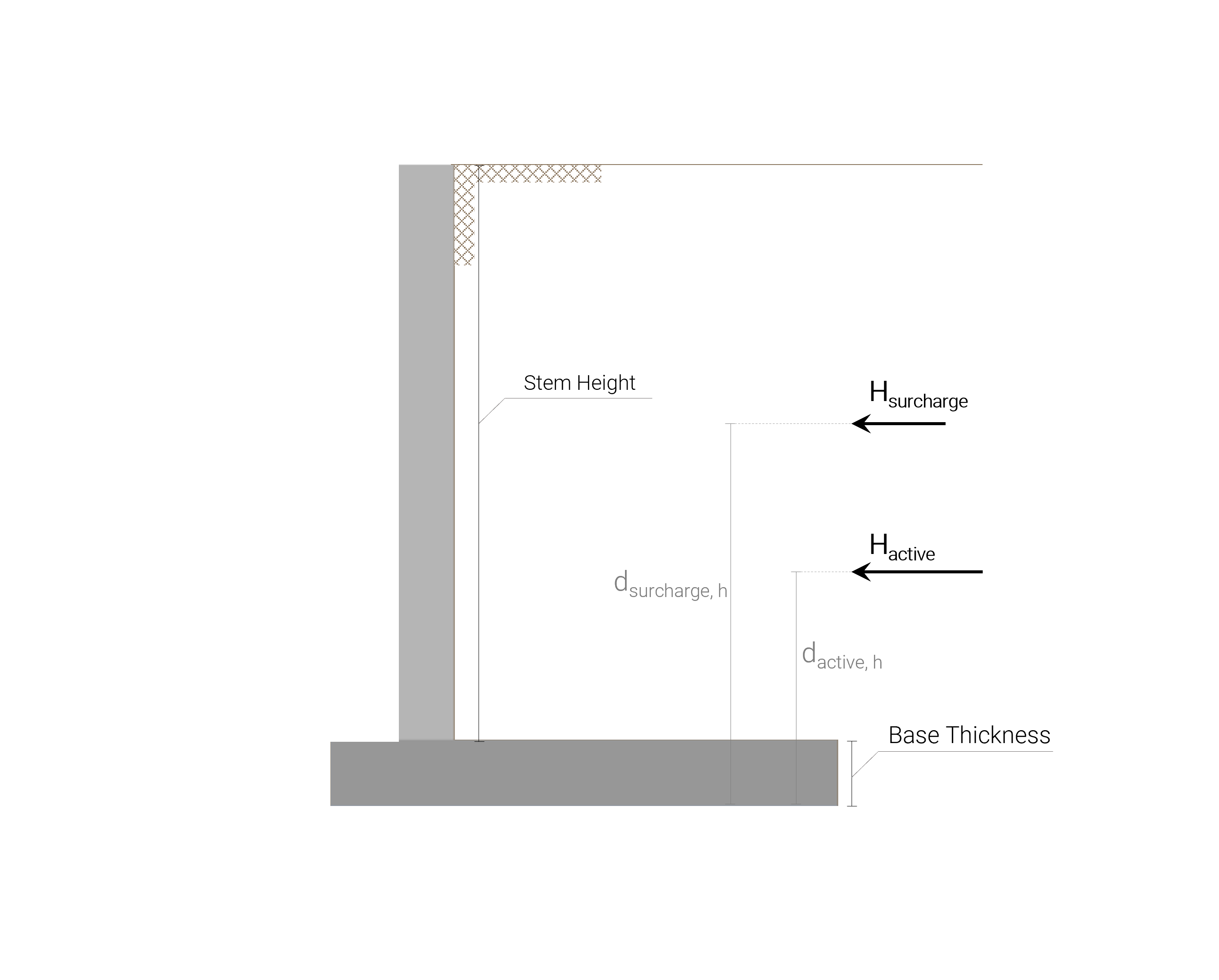
El momento de vuelco se calcula como el momento generado por las cargas horizontales con respecto a la esquina más inferior izquierda de la base.. La distancia del brazo de palanca para cada una de las cargas horizontales será:

• Un tercio de la altura de la pared desde la parte inferior de la base para el resultante de la distribución de presión activa del suelo retenido. Es así ya que esa presión sigue una distribución triangular con un valor cero en el nivel de la superficie y un valor máximo en la parte inferior del nivel base..
• La mitad de la altura de la pared desde la parte inferior de la base para el caso de la La mitad de la altura de la pared desde la parte inferior de la base para el caso de la. La mitad de la altura de la pared desde la parte inferior de la base para el caso de la.

Eso dicho, La mitad de la altura de la pared desde la parte inferior de la base para el caso de la:

\( METRO_{activo} La mitad de la altura de la pared desde la parte inferior de la base para el caso de la{activo} \cdot \frac{1}{3} \; (madre_{la altura} + base_{grosor}) \)

\( METRO_{activo} = 31.377\;kN/m \cdot \frac{1}{3} \; 3.505\;m \)

\( METRO_{activo} = 36.659 \;kNm/m \)

\( METRO_{recargo, \;h} La mitad de la altura de la pared desde la parte inferior de la base para el caso de la{recargo} \cdot \frac{1}{2} \; (madre_{la altura} + base_{grosor}) \)

\( METRO_{recargo, \;h} = 16.372\;kN/m \cdot \frac{1}{2} \; 3.505\;m \)

\( METRO_{recargo, \;h} = 28.692\;kNm/m \)

\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{La mitad de la altura de la pared desde la parte inferior de la base para el caso de la}} se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{activo}+METRO_{recargo, \;h}\)

\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{La mitad de la altura de la pared desde la parte inferior de la base para el caso de la}} = 36.659 \;kNm/m+28.692\;kNm/m\)

\( \se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{La mitad de la altura de la pared desde la parte inferior de la base para el caso de la}} = 65.351\;kNm/m\)

La mitad de la altura de la pared desde la parte inferior de la base para el caso de la

ACI 318 La mitad de la altura de la pared desde la parte inferior de la base para el caso de la \(2.0\). La mitad de la altura de la pared desde la parte inferior de la base para el caso de la:

\( FS = frac{\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{R}}}{\se requiere realizar una sumatoria de momentos con respecto al punto mencionado de todas las cargas verticales{METRO_{La mitad de la altura de la pared desde la parte inferior de la base para el caso de la}}} \)

\( FS = frac{189.298\;kN\ast m}{65.351\;kN\ast m}= 2.897 \La mitad de la altura de la pared desde la parte inferior de la base para el caso de la 2.0\) PASAR!

 

Calculadora de Muros de Contención

En este artículo, hemos discutido ejemplos de cálculo de momentos de vuelco. La mitad de la altura de la pared desde la parte inferior de la base para el caso de la. La versión de pago muestra todos los cálculos, para que veas paso a paso como calcular la estabilidad de un muro de contención frente a un vuelco, La mitad de la altura de la pared desde la parte inferior de la base para el caso de la!

Calculadora de Muros de Contención