En este artículo, desarrollaremos un ejemplo de diseño de losa utilizando la última versión de ACI-318-19: “Requisitos del Código de Construcción para Hormigón Estructural,” que consiste en el modelado en SkyCiv de un edificio de poca altura de hormigón armado que se centra en la comparación de los resultados del software y los cálculos manuales mediante un método aceptado por ACI: “El método de diseño directo para losas.” Este procedimiento consiste en asignar en diferentes franjas a lo largo de las direcciones principales y pórticos del edificio el momento total por factores convenientes para determinar la cantidad de refuerzo y la ubicación en la losa.

Esperamos que hayas leído el artículo anterior., Diseño de Placas en S3D, para introducirse en el modelado y diseño de placas usando SkyCiv. Otra información útil que le sugerimos que considere se encuentra en Como modelar placas? Una vez que complete la lectura de ambos documentos, siéntase libre de sumergirse en el siguiente ejemplo de comparación de losa completamente trabajado!

Disposición general del edificio

Las siguientes imágenes muestran una vista isométrica y dimensiones en planta del ejemplo a calcular. El edificio consta de dos losas planas elevadas sin vigas entre apoyos de pilares.

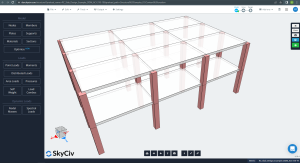
Figura 1. Vista isométrica del ejemplo de construcción.

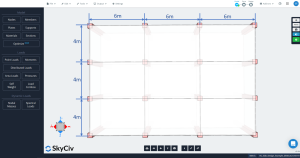
Figura 2. Dimensiones en planta de losa

Método de diseño directo para losas en dos direcciones (DDM)

Limitaciones

ACI 318 permite usar el DDM para diseñar losas de hormigón armado para cargas de gravedad, que reúnen unos requisitos según la geometría, relaciones de carga, simetría, etc.. Podemos resumir estas limitaciones en la siguiente lista (Notas PCA):

• “Debe haber tres o más tramos continuos en cada dirección.”: Figura 2 muestra tres tramos en cada dirección principal, longitudinales y transversales. OK!
• “Los paneles de losa deben ser rectangulares con una relación de luz más larga a más corta (línea central a línea central de soportes) no mayor que 2.”: Según figura 2, la relación es igual a \({\frac{l_1}{4}= frac{6m}{4m}=1.5 < 2}\). OK!
• “Longitudes de tramo sucesivas (línea central a línea central de soportes) en cada dirección no debe diferir en más de 1/3 del lapso más largo”. Las longitudes de tramo son las mismas en cada dirección, 6m a longitudinal y 4m a transversal. OK!
• “Las columnas no deben estar desplazadas más de 10% del lapso (en la dirección de compensación) desde cualquier eje entre líneas centrales de columnas sucesivas”. El ejemplo de construcción no tiene compensaciones en las columnas.. OK!
• “Las cargas deben distribuirse uniformemente, con la carga viva no factorizada o de servicio no más de dos veces la carga muerta no factorizada o de servicio (L/D ≤ 2)”. Tomando los valores de cada carga de gravedad, la relación se define como \({\frac{L}{re}= frac{2}{7.8}=0.256 < 2}\). OK!.
• “Para losas soportadas por vigas en dos direcciones, La rigidez relativa de las vigas en dos direcciones perpendiculares debe satisfacer los requisitos mínimos y máximos establecidos en el código.” Ya satisfecho; no hay vigas en las losas. OK!
• “No se permite la redistribución de momentos negativos por código.” Por la sencillez del ejemplo., no será necesario redistribuir momentos negativos en las losas. OK!.

Definición de franjas longitudinales y transversales

La losa en DDM debe dividirse en dos franjas principales para el análisis y diseño de una cuadrícula de líneas particular: columna y tiras intermedias. El ancho de las tiras de columnas es el menor de \({\frac {l_1}{4}}\) y \({\frac{l_2}{4}}\), dónde \({l_1}\) es la longitud del tramo a lo largo de la cuadrícula lineal y \({l_2}\) es la longitud transversal perpendicular.

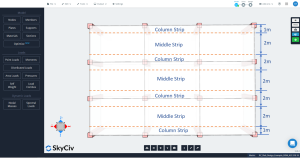
Figura 3. Columna longitudinal y franjas intermedias.

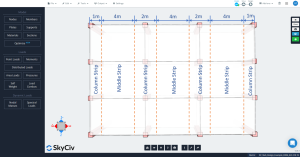
Figura 4. Columna transversal y franjas intermedias.

Grosor mínimo

ACI-318 sugiere usar la ecuación: \({A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{min}}= {\frac{l_n}{30}}={\frac{6m-0.50m}{30}}=0.1833m = 0.20m)

Comprobación preliminar de resistencia al corte

Antes de calcular el refuerzo de barras de acero, se recomienda comprobar la capacidad a cortante de la losa, uno para cortante directo en la conexión y otro para la resistencia a punzonamiento en la columna de la losa de conexión.

Para calcular la demanda de corte, usamos las siguientes cargas de gravedad:

• Losa de peso propio: \({SW={\gamma_c}\veces {A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{losa}}={24 {\frac{kN}{m ^ 3}}}\veces {0.20m}=4.8{\frac{kN}{m ^ 2}} }\)
• Carga muerta superpuesta: \({DE={3 {\frac{kN}{m ^ 2}}}}\)
• Carga muerta total (SO+SD): \({D = {7.8 {\frac{kN}{m ^ 2}}}}\)
• Carga viva (ocupación residencial) : \({L={2 {\frac{kN}{m ^ 2}}}}\)
• Carga de fuerza mayorada (1.2D+1.6L): \({q_{tu}={12.56 {\frac{kN}{m ^ 2}}}}\)

La primera comprobación de cortante es la “cortante de viga” tipo, donde la siguiente imagen indica el área a considerar para obtener el cortante total. Inspeccionamos cada dirección, tomando el área más extensa.

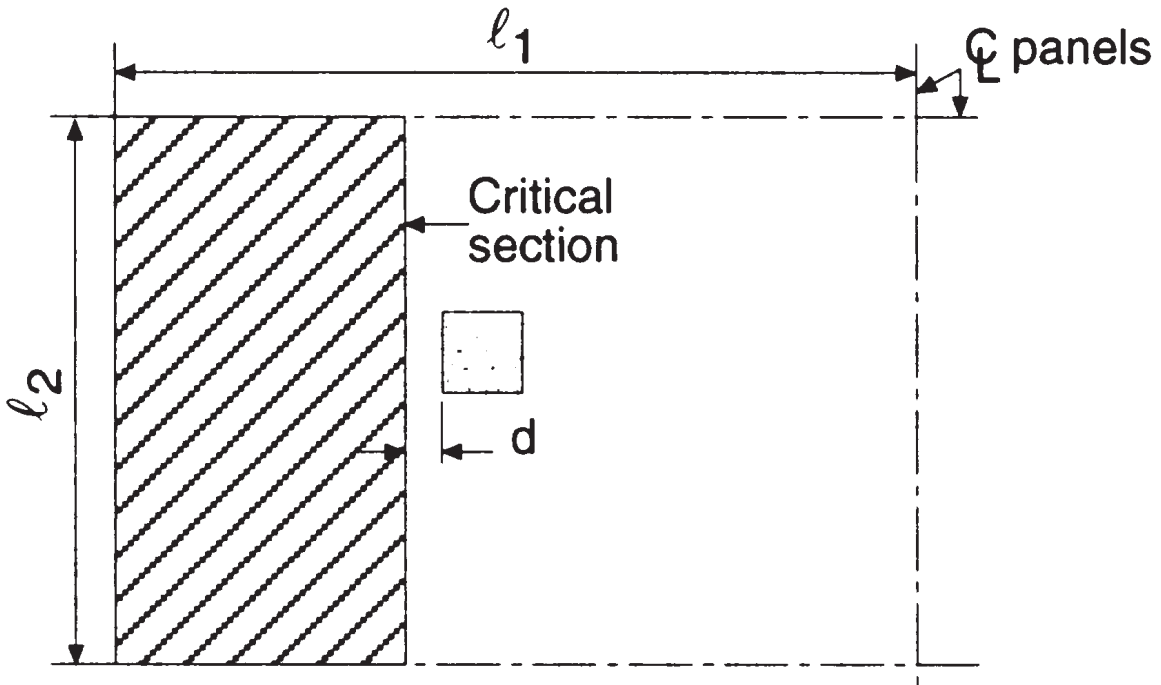
Figura 5. Cortante de viga en columna interior (Nadim Hassoun y Akthem AI-Manaseer, “Teoría y diseño del hormigón estructural”)

Dónde:

• Lapso de longitud en dirección longitudinal, \({l_1 = 6,0 m }\)
• Lapso de longitud en dirección transversal, \({l_2 = 4,0 m}\)
• Área tributaria total, cortante en dirección longitudinal \({A_t = l_2 veces (\frac{l_1}{2}-\frac{c_1}{2}-d) = 4,0 m veces (\frac{6.0m}{2}-\frac{0.50m}{2}-0.17m) = 10.32 m ^ 2}\) (seleccionado)
• Área tributaria total, cortante en dirección transversal, \({A_t = l_1 veces (\frac{l_2}{2}-\frac{c_2}{2}-d) = 6,0 m veces (\frac{4.0m}{2}-\frac{0.50m}{2}-0.17m) = 9.48 m ^ 2}\)
• Dimensión de columnas cuadradas, \({c_1 = c_2 = 0,50 m}\)
• Distancia d, \({re = h_{losa} – cubierta = 0,20 m – 0.03metro = 0,17 m }\)

Por lo tanto, el cortante máximo de la viga en la columna interior es

\({V_u =q_uveces A_t =12.56 {\frac{kN}{m ^ 2}}\veces 10.32 metro ^ 2 = 129.62 kN }\)

Esto se va a comparar con la resistencia al corte., \({\phi_sV_c}\)

• Resistencia del hormigón, \({f'_c = 25 MPa}\)
• Rendimiento de la resistencia del acero corrugado, \({f_y = 420 MPa}\)
• \({\fi_s = 0.75}\)
• \({\phi_sV_c = 0.17phi_slambdasqrt(f’_c) b_w d; b_w=l_2}\)

\({\phi_sV_c = 0,17veces 0,75veces 1veces sqrt(25 MPa) \veces 4000 mmveces 170 milímetro = 433.50 kN }\)

Podemos ver que la resistencia a cortante es mayor que la demanda de cortante: \({\phi_sV_c = 433.50 kN > v_u = 129.62 kN }\) OK!.

Según las siguientes imágenes, tenemos que calcular la capacidad de corte por punzonamiento y la fuerza a ser resistida por el hormigón en la conexión interior losa-columna. La intención del código al verificar el corte por punzonamiento es mantener valores bajos de esfuerzo cortante..

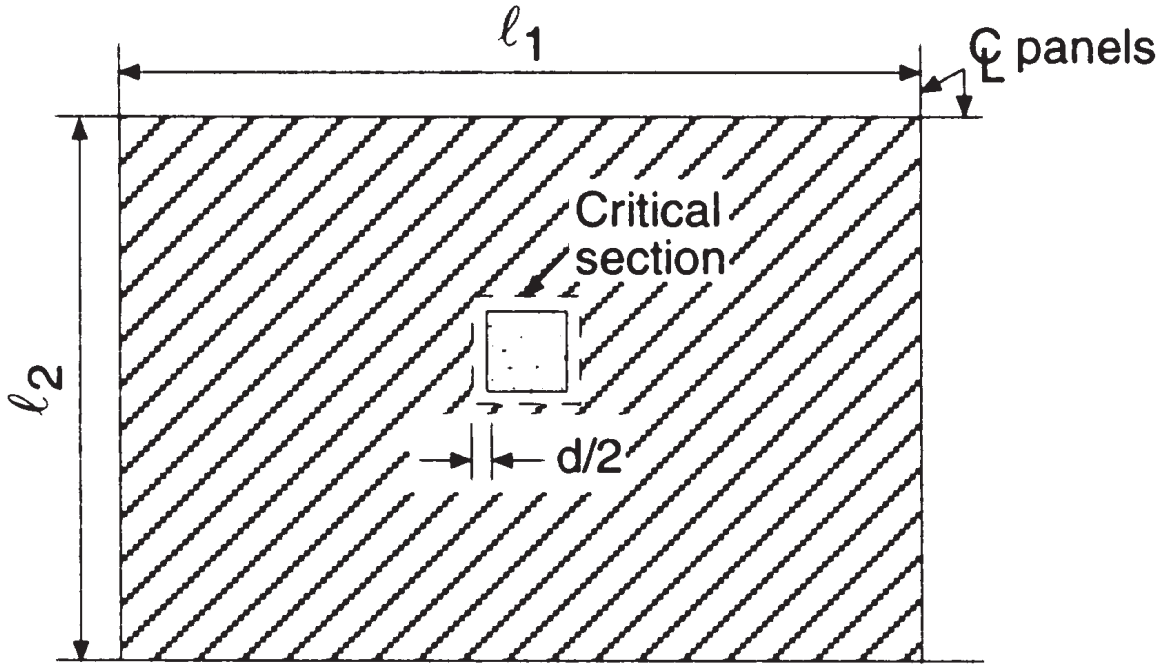
Figura 6. Cortante en dos direcciones en la columna interior (Nadim Hassoun y Akthem AI-Manaseer, “Teoría y diseño del hormigón estructural”)

• Área tributaria total, cizalla de perforación, \({A_t = l_1 times l_2 – (c_1+d)^2 = 6,0 m times 4,0 m – (0.50metro+0,17m)^2 = 23.55 m ^ 2}\) (misma área para ambas direcciones principales)

El esfuerzo cortante total a resistir es

\({V_u =q_uveces A_t =12.56 {\frac{kN}{m ^ 2}}\veces 23.55 metro ^ 2 = 295.79 kN }\)

Para obtener la capacidad de punzonamiento en una losa en dos direcciones, utilizaremos el método empírico establecido por el código ACI-318, que considera el esfuerzo cortante máximo disponible en el perímetro efectivo en la sección crítica. La expresión más conservadora para la columna interior es

• Capacidad de punzonamiento, \({\phi_sV_c = 0.33phi_slambdasqrt(f’_c) b_0 re; b_0=4veces (c_1+d)}\)

Por lo tanto, tenemos la resistencia a cortante de

\({\phi_sV_c = 0,33veces 0.75 \veces 1 \sqrt(25 MPa) \veces (4\veces (500 milímetro+170 milímetro)\veces 170 mm) = 563.81 kN }\)

Podemos ver que la resistencia a cortante es mayor que la demanda de cortante: \({\phi_sV_c = 563.81 kN > v_u = 295.75 kN }\) OK!.

Hemos verificado las demandas de cortante en una y dos direcciones en la conexión de la columna interior. Por ser ambas demandas inferiores a sus respectivas capacidades o resistencias, ahora pasaremos a calcular el refuerzo de la barra principal para la flexión de la losa.

Si eres nuevo en SkyCiv, Regístrese y pruebe el software usted mismo!

Regístrese en SkyCiv!

Momento estático mayorado total por vano.

El momento máximo que se puede desarrollar en una viga doble de extremo fijo es un momento isostático igual a \({M = frac{wveces {l_1}^ 2}{8}}\) (Ver figura 6).

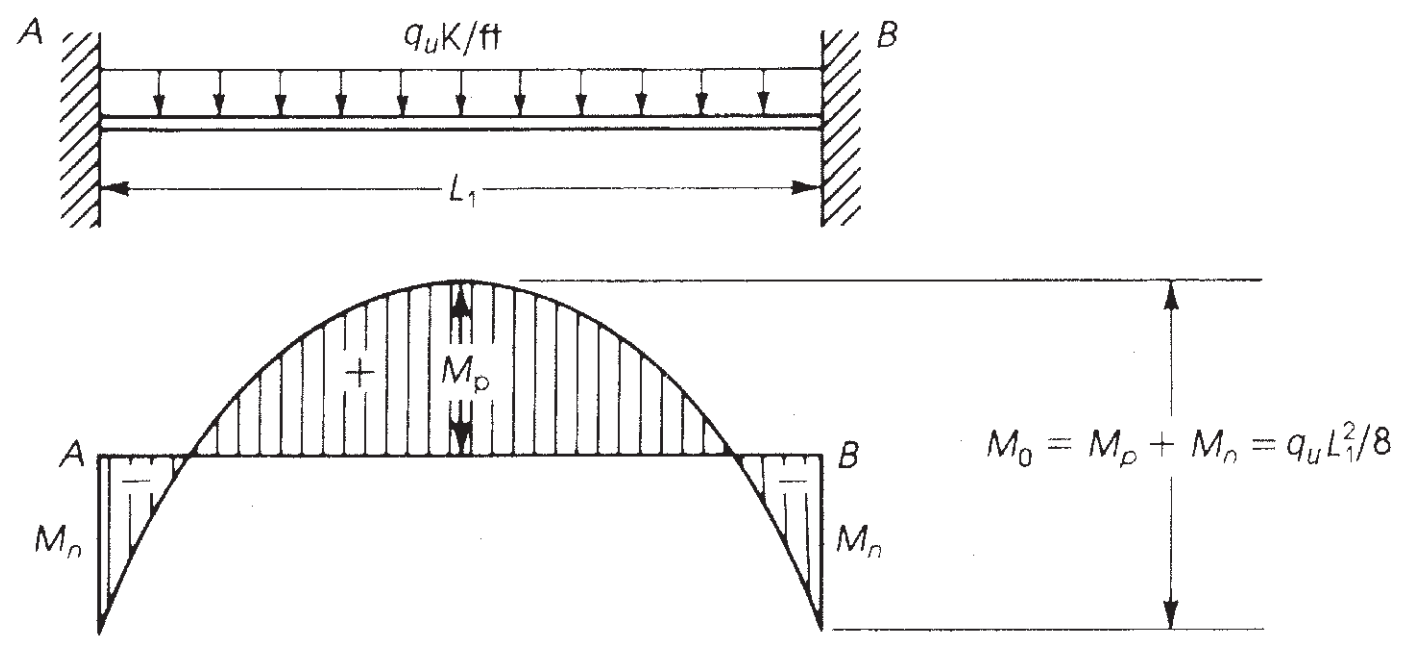
Figura 7. Momento flector en una viga de extremo fijo. (Nadim Hassoun y Akthem AI-Manaseer, “Teoría y diseño del hormigón estructural”)

ACI-18 toma este principio y, para el método de diseño directo (DDM), establece el momento estático máximo a considerar por vano \({M_0}\)

Dirección longitudinal:

• \({M_0 = frac {q_uveces l_2veces {l_{norte,1}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{kN}{m ^ 2}}\veces 4.0mveces (6m-0.50m)^ 2}{8}=189,97 kN-m}\)

Dirección transversal:

• \({M_0 = frac {q_uveces l_1veces {l_{norte,2}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{kN}{m ^ 2}}\veces 6.0mveces (4m-0.50m)^ 2}{8}=115,40 kN-m}\)

El siguiente paso es asignar este momento total considerando el tipo de panel, interiores o exteriores. (Ver figura 7). Después, debido a que los vanos son continuos, es necesario dividir también el momento en positivo y negativo. Esto último se muestra en imágenes. 8 y 9.

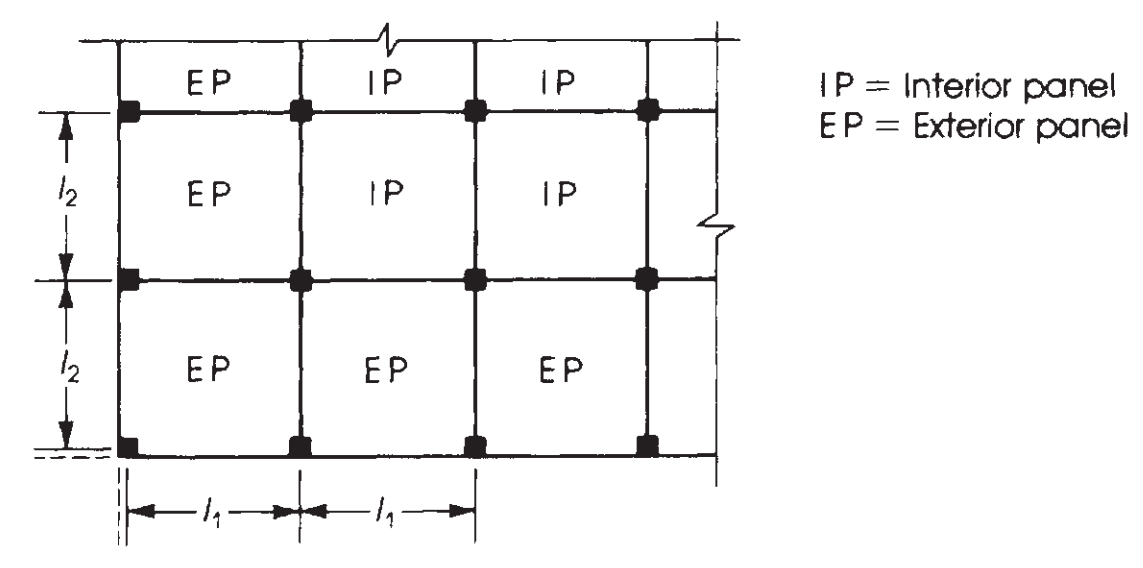
Figura 8. Definición de paneles según su posición relativa en un plano de losa. (Nadim Hassoun y Akthem AI-Manaseer, “Teoría y diseño del hormigón estructural”)

 

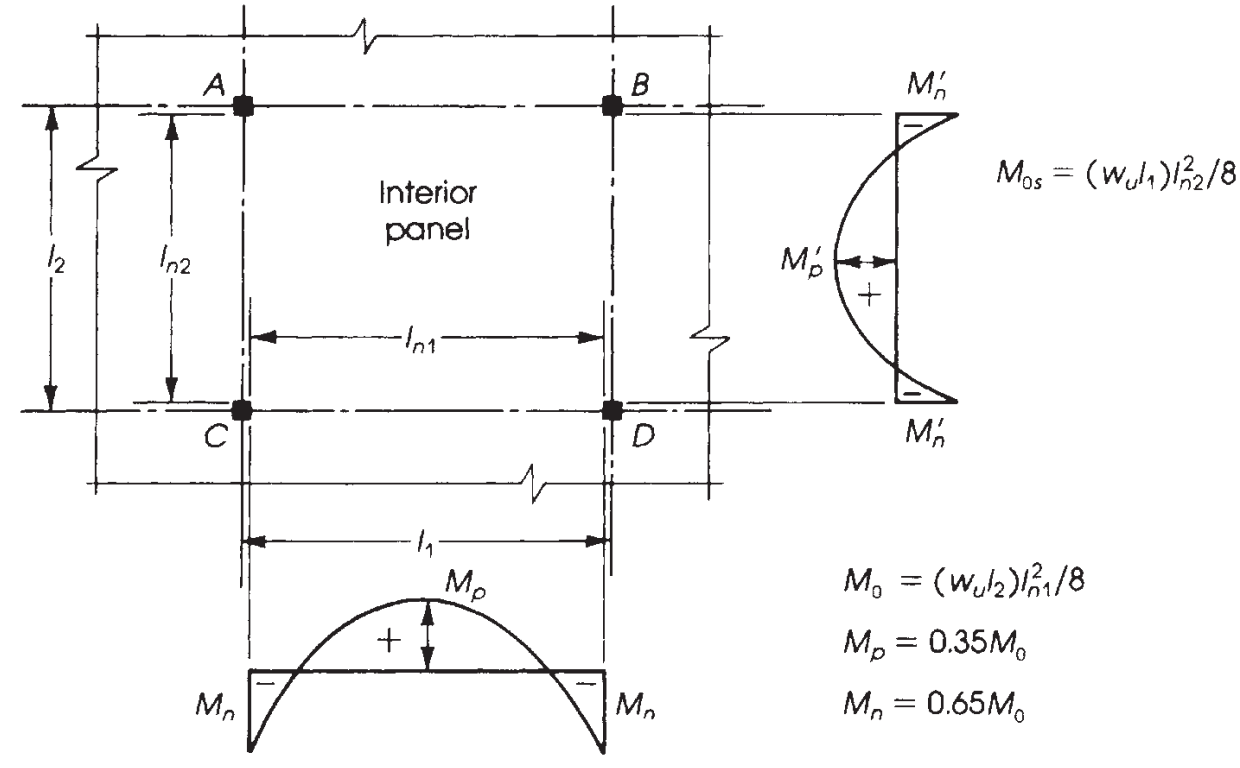
Figura 9. Distribución de momentos en un panel interior. (Nadim Hassoun y Akthem AI-Manaseer, “Teoría y diseño del hormigón estructural”)

 

Es fundamental conocer la correcta distribución de momentos en función de la losa que estemos diseñando. En este ejemplo, tenemos el ultimo caso en la siguiente imagen (figura 9), “Sin vigas,” aplicado a una losa plana o losa maciza sin ninguna viga, ni en el borde ni entre soportes.

La principal diferencia en los cinco casos que se muestran en la figura 9 es las fracciones de momentos que se van a asignar en los paneles exteriores, en el que la coacción relativa al final cambia los valores a calcular.

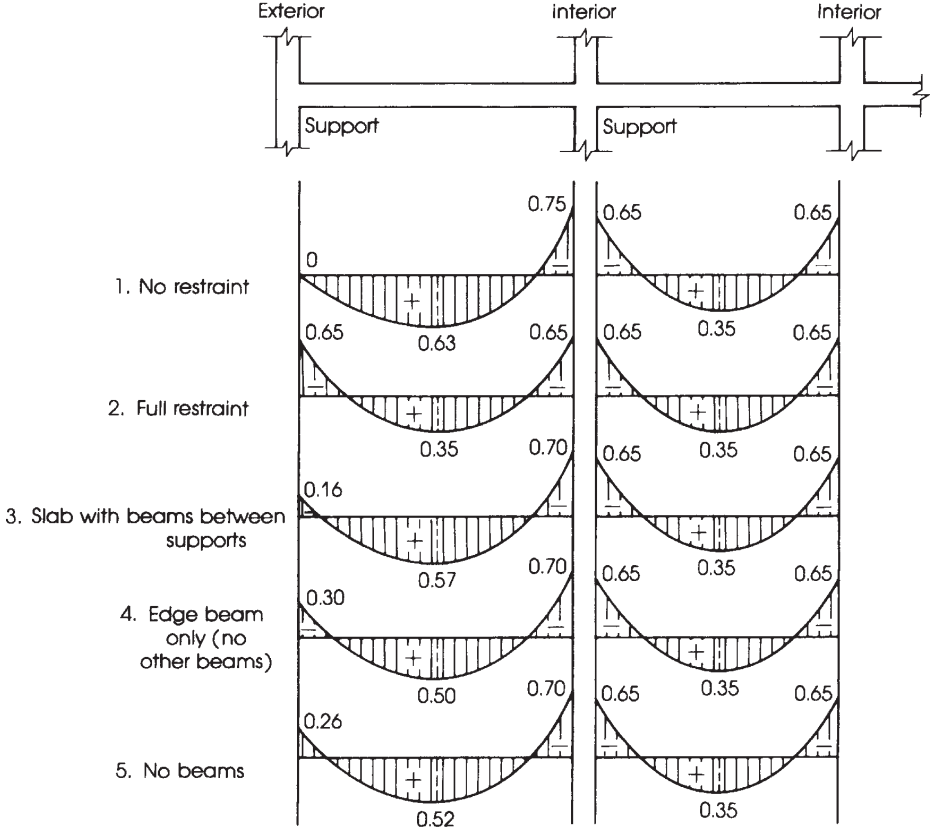
Figura 10. Distribución del momento estático total en momentos de tramo negativos y positivos. (Nadim Hassoun y Akthem AI-Manaseer, “Teoría y diseño del hormigón estructural”)

Distribución del momento total mayorado \({M_0}\) por vano en momentos negativos y positivos.

Una vez \({M_0}\) ha sido calculado, es hora de asignar la fracción de momentos en positivo y negativo en cada franja de diseño, es decir, columna y tiras intermedias. Para más claridad, figura 10 ayuda a especificar el factor apropiado a considerar en la distribución del momento total.

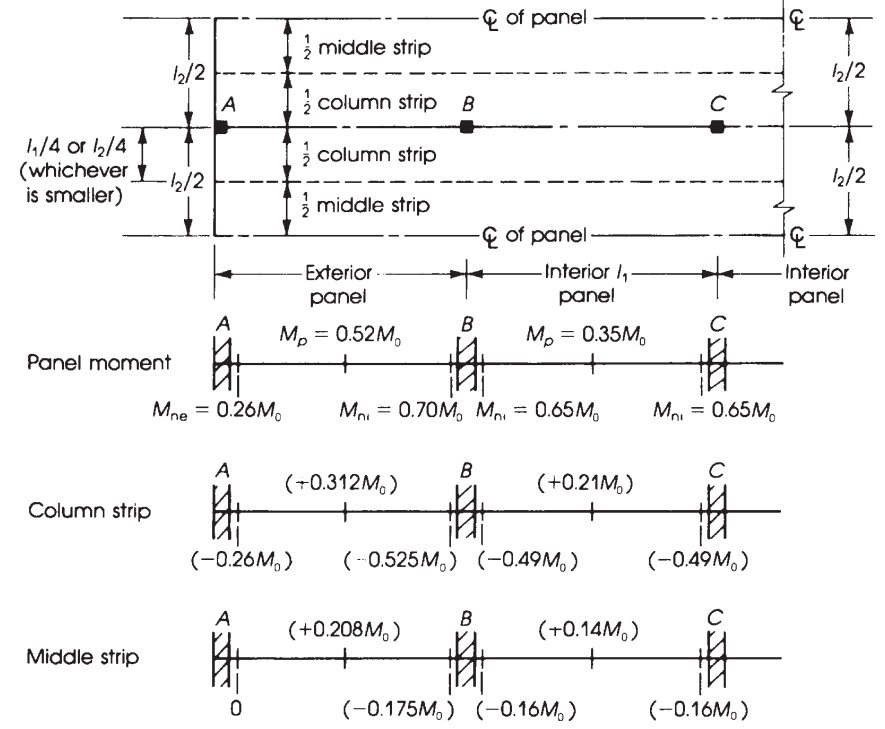
Figura 11. Ancho del marco rígido equivalente y distribución de momentos en losas planas. (Nadim Hassoun y Akthem AI-Manaseer, “Teoría y diseño del hormigón estructural”)

Utilizando los factores anteriores indicados en la figura 10, obtenemos en la siguiente tabla el momento último.

Dirección longitudinal: \({M_0 = 189.97 kN-m}\)

Lapso (ES:Exterior, ES:Interior)	momento total (kN-m)	Momento de tira de columna (kN-m)	Momento de franja media (kN-m)
Exterior Negativo ES	0.26M0=49.39	0.26M0=49.39	0
ES positivo	0.52M0=98.78	0.31M0=58,89	0.21M0=39.89
Interior Negativo ES	0.70M0=132,98	0.53M0=100,68	0.17M0=32.29
ES positivo	0.35M0=66,49	0.21M0=39.89	0.14M0=26,60
ES negativo	0.65M0=123,48	0.49M0=93.09	0.16M0=30,40

Con el momento una vez distribuido, es hora de determinar el refuerzo de barras de acero que se colocará en la losa. Solo desarrollaremos un cálculo y luego todos los resultados en una tabla..

Momento en el vano negativo exterior en la tira de pilares, \({M_u = 49.39 kN-m}\)

• Supuesta sección controlada por tensión. \({\fi_f = 0.9}\)
• Ancho de tira de columna, \({b=2.0m}\)
• Zona de refuerzo de acero, \({A_s = frac{M_u}{\phi_fveces 0.9dveces fy}= frac{49.39kN-m}{0.9\veces 0.9(0.17m)\veces 420 MPa}=853.996 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de refuerzo de acero, \({UNA_{s,min}=rho_{min}\veces bveces d = 0.0018 \veces 2.0m veces 0.17m =612 {mm}^ 2}\). Ahora, comprobar si la sección se comporta como controlada por tensión.
• \({a = frac{A_sveces f_y}{0.85\veces f'cveces b} = frac{853.996 {mm}^2veces 420 MPa}{0.85\veces 25 MPaveces 2,0m }= 8.439 mm}\)
• \({c = frac{a}{\beta_1}= frac{8.439 mm}{0.85} = 9,929 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\veces d – 0.003 = (\frac{0.003}{9.929mm})\veces 170 mm – 0.003 = 0.048 > 0.005 }\) OK!, es una sección controlada por tensión!.

Lapso(ES:Exterior, ES:Interior)	Momento de tira de columna (kN-m)	\({UNA_{s,calcular} ({mm}^ 2)}\)	\({UNA_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	49.39	853.996	612.0	8.439	9.929	0.048 > 0.005!
ES positivo	58.89	1018.259	612.0	10.063	11.839	0.040 > 0.005!
Interior Negativo ES	100.68	1740.844	612.0	17.204	20.24	0.022 > 0.005!
ES positivo	39.89	689.733	612.0	6.816	8.019	0.06 > 0.005!
ES negativo	93.09	1609.607	612.0	15.907	18.714	0.024 > 0.005!

Momento en el vano positivo exterior en la franja central, \({M_u = 39.89 kN-m}\)

• Supuesta sección controlada por tensión. \({\fi_f = 0.9}\)
• Ancho de tira medio, \({b=2.0m}\)
• Zona de refuerzo de acero, \({A_s = frac{M_u}{\phi_fveces 0.9dveces fy}= frac{39.89kN-m}{0.9\veces 0.9(0.17m)\veces 420 MPa}=689.733 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de refuerzo de acero, \({UNA_{s,min}=rho_{min}\veces bveces d = 0.0018 \veces 2.0m veces 0.17m =612 {mm}^ 2}\). Ahora, comprobar si la sección se comporta como controlada por tensión.
• \({a = frac{A_sveces f_y}{0.85\veces f'cveces b} = frac{689.766 {mm}^2veces 420 MPa}{0.85\veces 25 MPaveces 2,0m }= 6.816 mm}\)
• \({c = frac{a}{\beta_1}= frac{6.816 mm}{0.85} = 8.019 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\veces d – 0.003 = (\frac{0.003}{8.019mm})\veces 170 mm – 0.003 = 0.0605 > 0.005 }\) OK!, es una sección controlada por tensión!.

Lapso(ES:Exterior, ES:Interior)	Momento de la franja media (kN-m)	\({UNA_{s,calcular} ({mm}^ 2)}\)	\({UNA_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	0	0.00	612.0	6.048	7.115	0.069 > 0.005!
ES positivo	39.89	689.733	612.0	6.816	8.019	0.061 > 0.005!
Interior Negativo ES	32.29	558.322	612.0	6.048	7.115	0.069 > 0.005!
ES positivo	26.60	459.937	612.0	6.048	7.115	0.069 > 0.005!
ES negativo	30.40	525.642	612.0	6.048	7.115	0.069 > 0.005!

Dirección transversal: \({M_0 = 115.40 kN-m}\)

Lapso (ES:Exterior, ES:Interior)	momento total (kN-m)	Momento de tira de columna (kN-m)	Momento de franja media (kN-m)
Exterior Negativo ES	0.26M0=30.00	0.26M0=30.00	0
ES positivo	0.52M0=60,00	0.31M0=35,77	0.21M0=24,23
Interior Negativo ES	0.70M0=80,78	0.53M0=61,16	0.17M0=19,62
ES positivo	0.35M0=40.39	0.21M0=24,23	0.14M0=16,16
ES negativo	0.65M0=75.01	0.49M0=56,55	0.16M0=18,46

Con el momento una vez distribuido, es hora de determinar el refuerzo de barras de acero para colocar en la losa. Solo desarrollaremos un cálculo y luego todos los resultados en una tabla..

Momento en el vano negativo exterior en la tira de pilares, \({M_u = 30.00 kN-m}\)

• Supuesta sección controlada por tensión. \({\fi_f = 0.9}\)
• Ancho de tira de columna, \({b=2.0m}\)
• Zona de refuerzo de acero, \({A_s = frac{M_u}{\phi_fveces 0.9dveces fy}= frac{30.00kN-m}{0.9\veces 0.9(0.17m)\veces 420 MPa}=518.726 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de refuerzo de acero, \({UNA_{s,min}=rho_{min}\veces bveces d = 0.0018 \veces 2.0m veces 0.17m =612 {mm}^ 2}\). Ahora, comprobar si la sección se comporta como controlada por tensión.
• \({a = frac{A_sveces f_y}{0.85\veces f'cveces b} = frac{518.726 {mm}^2veces 420 MPa}{0.85\veces 25 MPaveces 2,0m }= 6.048 mm}\)
• \({c = frac{a}{\beta_1}= frac{6.048 mm}{0.85} = 7,115 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\veces d – 0.003 = (\frac{0.003}{7.115mm})\veces 170 mm – 0.003 = 0.069 > 0.005 }\) OK!, es una sección controlada por tensión!.

Lapso(ES:Exterior, ES:Interior)	Momento de tira de columna (kN-m)	\({UNA_{s,calcular} ({mm}^ 2)}\)	\({UNA_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	30.00	518.726	612.0	6.048	7.115	0.069 > 0.005!
ES positivo	35.77	618.494	612.0	6.112	7.191	0.068 > 0.005!
Interior Negativo ES	61.16	1057.509	612.0	10.451	12.295	0.038 > 0.005!
ES positivo	24.23	418.958	612.0	6.048	7.115	0.069 > 0.005!
ES negativo	56.55	977.799	612.0	9.663	11.368	0.042 > 0.005!

Momento en el vano positivo exterior en la franja central, \({M_u = 24.23 kN-m}\)

• Supuesta sección controlada por tensión. \({\fi_f = 0.9}\)
• Ancho de tira de columna, \({b=4,0m}\)
• Zona de refuerzo de acero, \({A_s = frac{M_u}{\phi_fveces 0.9dveces fy}= frac{24.23 kN-m}{0.9\veces 0.9(0.17m)\veces 420 MPa}=418.958 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Área mínima de refuerzo de acero, \({UNA_{s,min}=rho_{min}\veces bveces d = 0.0018 \veces 4.0m veces 0.17m =1224 {mm}^ 2}\). Ahora, comprobar si la sección se comporta como controlada por tensión.
• \({a = frac{A_sveces f_y}{0.85\veces f'cveces b} = frac{1224 {mm}^2veces 420 MPa}{0.85\veces 25 MPaveces 4,0m }= 6.048 mm}\)
• \({c = frac{a}{\beta_1}= frac{6.048 mm}{0.85} = 7.115 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\veces d – 0.003 = (\frac{0.003}{7.115mm})\veces 170 mm – 0.003 = 0.069 > 0.005 }\) OK!, es una sección controlada por tensión!.

Lapso(ES:Exterior, ES:Interior)	Momento de la franja media (kN-m)	\({UNA_{s,calcular} ({mm}^ 2)}\)	\({UNA_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Exterior Negativo ES	0.00	0.00	1224.00	6.048	7.115	0.069 > 0.005!
ES positivo	24.23	418.958	1224.00	6.048	7.115	0.069 > 0.005!
Interior Negativo ES	19.62	339.247	1224.00	6.048	7.115	0.069 > 0.005!
ES positivo	16.16	279.420	1224.00	6.048	7.115	0.069 > 0.005!
ES negativo	18.46	319.189	1224.00	6.048	7.115	0.069 > 0.005!

Si eres nuevo en SkyCiv, Regístrese y pruebe el software usted mismo!

Regístrese en SkyCiv!

Módulo de diseño SkyCiv S3D

En esta sección, describimos el resultado del diseño utilizando el módulo para el diseño de placas incluido en SkyCiv. No explicamos cómo modelar y analizar la estructura. (para éstos, ver artículos relacionados sobre este tema en nuestra documentación: Cómo modelar una estructura en SkyCiv?, Cómo aplicar cargas en mi modelo de construcción? y Cómo ejecutar un análisis elástico lineal?)

Es conveniente aplicar una malla fina a las losas para obtener un resultado de diseño preciso. Por favor, eche un vistazo a la siguiente imagen para mayor claridad..

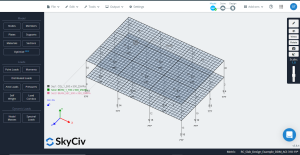
Figura 12. Malla más fina aplicada a losas

El siguiente paso es ejecutar el módulo de diseño y seleccionar las opciones que calculan un área de barras de refuerzo de acero optimizada.

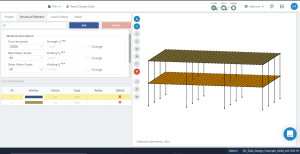
Figura 13. Definición de las propiedades del hormigón de losa antes de la optimización del diseño.

Figura 14 representa la orientación de los ejes locales de la placa. Porque el eje local 3 es hacia abajo, la “superior” es el fondo, y el “inferior” será la parte superior, tomando así correctamente los datos del diseño.

Otro dato importante es el tamaño de malla de la losa.; es un elemento cuadrado de placa con dimensiones en planta de 500 mm x 500 mm. SkyCiv S3D proporciona el área de refuerzo como un valor integrado por elemento finito. Así, si queremos obtener el área total de armadura de una columna o franja intermedia, necesitamos calcular el valor medio a partir del número de elementos que suman el ancho de la tira que se está analizando. Por ejemplo, para la tira de columna, Se considerarán cuatro elementos. (4×0.5metro = 2m).

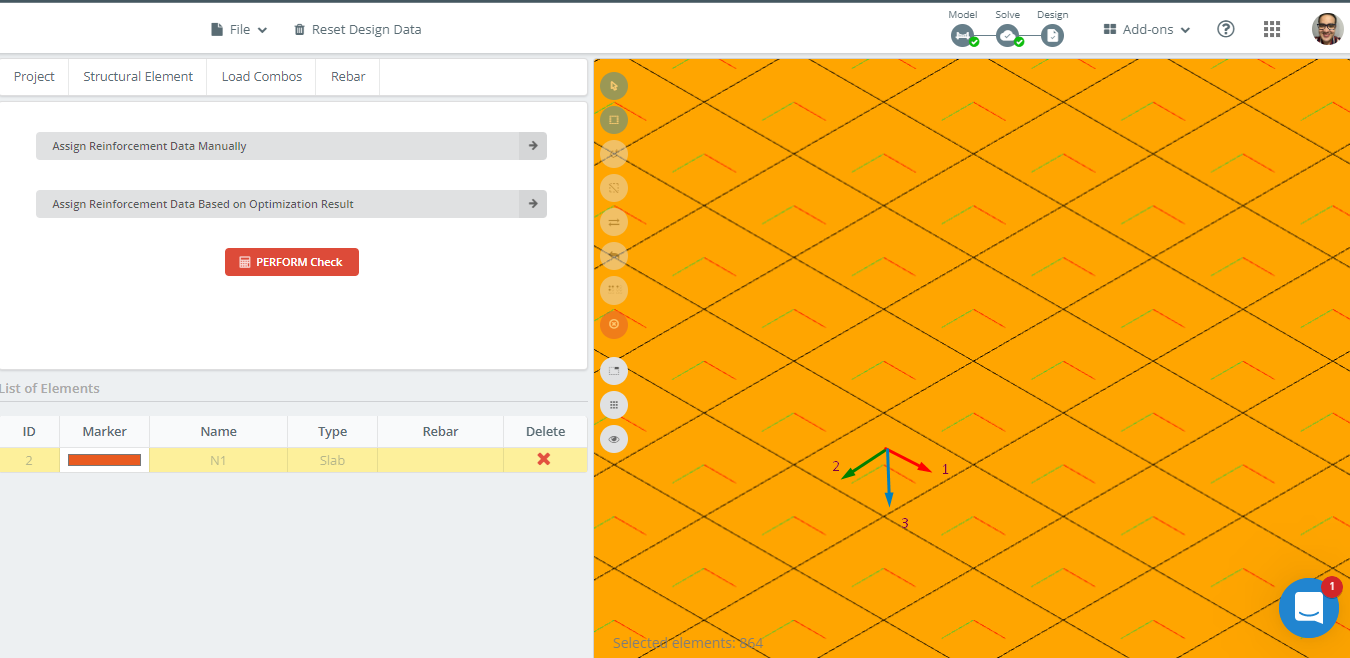
Figura 14. Ejemplo de orientación de ejes locales en losa.

primero, analizamos el área de refuerzo requerida a lo largo de la dirección longitudinal en el eje 1.

Tira de columna

• Momento negativo exterior (refuerzo superior): \({UNA_{s,superior} =(119.09\veces 2 + 952.72 + 833.64 )\frac{{mm}^ 2}{m} \veces 0.50m = 1012.27 {mm}^ 2}\)
• Momento positivo exterior (refuerzo inferior): \({UNA_{s,larva del moscardón} = 4*463.90 \frac{{mm}^ 2}{m}\veces 0.50m = 927.80 {mm}^ 2}\)
• Momento negativo interior exterior (refuerzo superior): \({UNA_{s,superior} =(1071.82\veces 2 +714.54 \veces 2 )\frac{{mm}^ 2}{m} \veces 0.50m = 1786.36 {mm}^ 2}\)
• Momento interior positivo(refuerzo inferior): \({UNA_{s,larva del moscardón} = 4*309.27 \frac{{mm}^ 2}{m}\veces 0.50m = 618.54 {mm}^ 2}\)
• Momento negativo interior (refuerzo superior): \({UNA_{s,superior} =(714.54\veces 2 +952.73 \veces 2 )\frac{{mm}^ 2}{m} \veces 0.50m = 1667.27 {mm}^ 2}\)

tira media

• Momento negativo exterior (refuerzo superior): \({UNA_{s,superior} =(119.09\veces 4)\frac{{mm}^ 2}{m} \veces 0.50m = 238.18 {mm}^ 2}\)
• Momento positivo exterior (refuerzo inferior): \({UNA_{s,larva del moscardón} = (463.90\veces 2 +412.36 \veces 2 ) \frac{{mm}^ 2}{m}\veces 0.50m = 876.26 {mm}^ 2}\)
• Momento negativo interior exterior (refuerzo superior): \({UNA_{s,superior} =(357.27\veces 2 +476.36 \veces 2 )\frac{{mm}^ 2}{m} \veces 0.50m = 833.63 {mm}^ 2}\)
• Momento interior positivo(refuerzo inferior): \({UNA_{s,larva del moscardón} = 4*257.72 \frac{{mm}^ 2}{m}\veces 0.50m = 515.44 {mm}^ 2}\)
• Momento negativo interior (refuerzo superior): \({UNA_{s,superior} =(357.27\veces 2 +476.36 \veces 2 )\frac{{mm}^ 2}{m} \veces 0.50m = 833.63 {mm}^ 2}\)

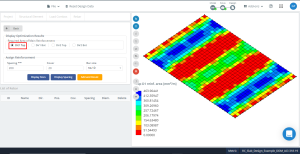
Figura 15. Resultados de optimización en dirección “1” y el lado superior (Lado inferior, Realmente).

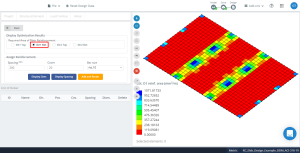
Figura 16. Resultados de optimización en dirección “1” y el lado inferior (Lado superior, Realmente).

Finalmente, analizamos el área de refuerzo requerida a lo largo de la dirección transversal en el eje 2.

Tira de columna

• Momento negativo exterior (refuerzo superior): \({UNA_{s,superior} =(91.55\veces 2 + 457.73 + 549.28 )\frac{{mm}^ 2}{m} \veces 0.50m = 595.055 {mm}^ 2}\)
• Momento positivo exterior (refuerzo inferior): \({UNA_{s,larva del moscardón} = (269.68\veces 3+239.72) \frac{{mm}^ 2}{m}\veces 0.50m = 524.38 {mm}^ 2}\)
• Momento negativo interior exterior (refuerzo superior): \({UNA_{s,superior} =(823.92\veces 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \veces 0.50m = 1327.43 {mm}^ 2}\)
• Momento interior positivo(refuerzo inferior): \({UNA_{s,larva del moscardón} = (179.79\veces 3+149.82) \frac{{mm}^ 2}{m}\veces 0.50m = 344.60 {mm}^ 2}\)
• Momento negativo interior (refuerzo superior): \({UNA_{s,superior} =(823.92\veces 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \veces 0.50m = 1327.43 {mm}^ 2}\)

tira media

• Momento negativo exterior (refuerzo superior): \({UNA_{s,superior} =(183.09\veces 2+91.55veces 6)\frac{{mm}^ 2}{m} \veces 0.50m = 457.74 {mm}^ 2}\)
• Momento positivo exterior (refuerzo inferior): \({UNA_{s,larva del moscardón} = (209.75\veces 2 +179.79 \veces 2 +149.82 \veces 4) \frac{{mm}^ 2}{m}\veces 0.50m = 689.18{mm}^ 2}\)
• Momento negativo interior exterior (refuerzo superior): \({UNA_{s,superior} =(274.64\veces 2+91.55veces 6)\frac{{mm}^ 2}{m} \veces 0.50m = 549.29 {mm}^ 2}\)
• Momento interior positivo(refuerzo inferior): \({UNA_{s,larva del moscardón} = (119.86\veces 4 + 89.89\veces 4) \frac{{mm}^ 2}{m}\veces 0.50m = 419.50 {mm}^ 2}\)
• Momento negativo interior (refuerzo superior): \({UNA_{s,superior} =(274.64\veces 2+91.55veces 6 )\frac{{mm}^ 2}{m} \veces 0.50m = 549.29 {mm}^ 2}\)

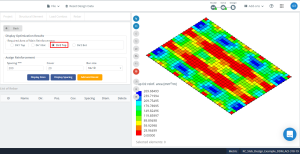
Figura 17. Resultados de optimización en dirección “2” y el lado superior (Lado inferior, Realmente).

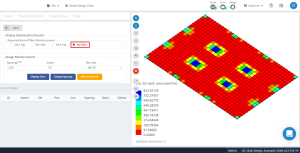
Figura 18. Resultados de optimización en dirección “2” y el lado inferior (Lado superior, Realmente).

 

Comparación de resultados

La siguiente tabla muestra los resultados para el DDM (“Método de diseño directo”) y la optimización de barras de refuerzo de acero S3D.

Lapso (ES:Exterior, ES:Interior)	Tira de columna (Diseño S3D) \({Como ({mm}^ 2)}\)	Tira de columna (ACI-318 DDM) \({Como ({mm}^ 2)}\)	% diferencia	tira media (Diseño S3D) \({Como ({mm}^ 2)}\)	tira media (ACI-318 DDM) \({Como ({mm}^ 2)}\)	% diferencia
Exterior Negativo ES	1012.27	853.996	15.636	238.18	0 (612.0)	100.00
ES positivo	927.80	1018.259	9.75	876.26	689.733	21.287
Interior Negativo ES	1786.36	1740.844	2.48	833.63	558.322 (612.0)	26.586
ES positivo	618.54	689.733	11.51	515.44	459.937 (612.0)	18.734
ES negativo	1667.27	1609.607	3.459	833.63	525.642 (612.0)	26.586

Dirección transversal

Lapso (ES:Exterior, ES:Interior)	Tira de columna (Diseño S3D) \({Como ({mm}^ 2)}\)	Tira de columna (ACI-318 DDM) \({Como ({mm}^ 2)}\)	% diferencia	tira media (Diseño S3D) \({Como ({mm}^ 2)}\)	tira media (ACI-318 DDM) \({Como ({mm}^ 2)}\)	% diferencia
Exterior Negativo ES	595.055	518.726	12.827	457.74	0 (1224)	100.00
ES positivo	524.38	618.494	17.948	689.18	418.958	39.209
Interior Negativo ES	1327.43	1057.509	20.334	549.29	339.247	38.239
ES positivo	344.60	418.958	21.578	419.50	279.42	33.392
ES negativo	1327.43	977.799	26.339	549.29	319.189	41.891

Conclusión

Hemos demostrado en este artículo que el módulo SkyCiv para el diseño de placas calcula el refuerzo de acero para la losa de flexión de acuerdo con el código ACI-318-19. Comparación de los resultados del análisis en las tiras de columna, donde debido a su relativa rigidez, los momentos están muy concentrados, las diferencias entre los cálculos manuales y la optimización por S3D rondan un valor de 10 – 15%. Esta practicidad indica una excelente combinación entre los procedimientos de análisis y diseño..

Para tiras intermedias, los resultados difieren un poco más porque el código solo asigna el resto del momento después de tomar las tiras de columna correspondientes. Esto afectará el partido cuando lo comparemos con el análisis del software., que es mas exacto.

Nuevo en SkyCiv? Regístrese y pruebe el software usted mismo!

Regístrese en SkyCiv!