Un recorrido por los cálculos para diseñar una zapata aislada. (ACI 318-14)
La base es un sistema de construcción esencial que transfiere las fuerzas de la columna y la pared al suelo de soporte.. El ingeniero puede optar por un sistema de cimentación poco profundo o profundo según las características del suelo y las cargas del edificio..
Módulo de diseño de la Fundación SkyCiv Incluye análisis y diseño de zapatas aisladas conforme al código americano ACI318-14..
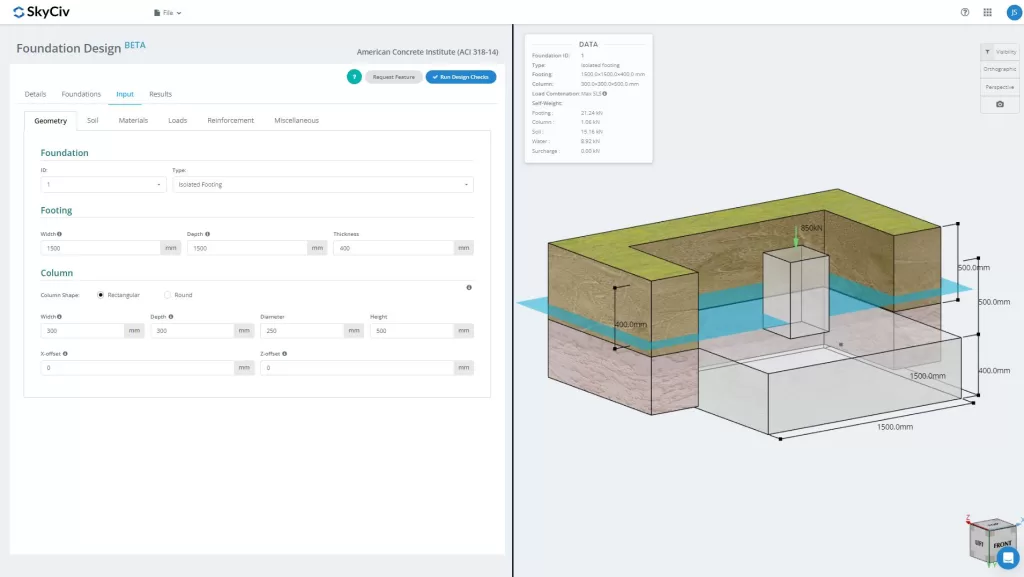
¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta permite a los usuarios realizar cálculos de diseño de cimientos sin descargar ni instalar!
Una guía paso a paso para diseñar una zapata aislada
Requisitos de dimensión
Para determinar las dimensiones de una zapata aislada, servicio o cargas no factorizadas, como muerto (re), En Vivo (L), Viento (W), Sísmico (E), etc. se aplicará utilizando combinaciones de carga, según lo definido por ACI 318-14. Cualquier combinación de carga que gobierne se considerará la carga de diseño, y se compara con la presión de suelo permitida como se muestra en la ecuación 1, como se recomienda en Sección de 13.2.6 de ACI 318-14.
\(\texto{q}_ _{\texto{a}} = frac{\texto{PAG}_ _{\texto{norte}}}{\texto{A}} \flecha correcta \) Ecuación 1
qa = Presión permitida del suelo
PAGnorte = Carga de diseño no mayorada
A = área de cimentación
Las dimensiones de la zapata se pueden estimar inicialmente resolviendo el área de cimentación. (A) usando la ecuación 1.
\(\texto{A} = frac{\texto{PAG}_ _{\texto{norte}}}{\texto{q}_ _{\texto{a}}} \flecha correcta \) Ecuación 1a
Cizalla unidireccional
El estado límite de corte unidireccional, también conocido como corte de viga, reconoce que la zapata puede fallar en corte similar a una viga ancha a lo largo de un plano de corte crítico ubicado a una distancia “d” desde la cara de la columna (Figura 1),
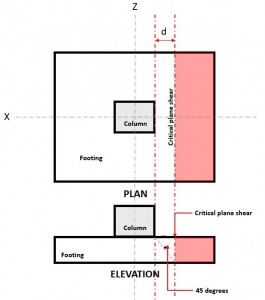
Figura 1. Corte crítico en plano de corte unidireccional
El De una sola mano Corte Demanda o V tu se calcula asumiendo que la base está en voladizo lejos de la columna donde se indica el área roja en la Figura 1, siguiente Sección de 8.5.3.1.1.
El Capacidad de corte unidireccional o ϕVc se define como la resistencia máxima al corte y se calcula utilizando la ecuación 2 por Sección de 22.5.5.1.
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 2 \sqrt{\texto{F'}_ _{\texto{c}}} \tiempos texto{b}_ _{\texto{w}} \tiempos texto{d} \flecha correcta \) Ecuación 2 ( Sección de 22.5.5.1, Imperial)
o
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 0.17 \sqrt{\texto{F'}_ _{\texto{c}}} \tiempos texto{b}_ _{\texto{w}} \tiempos texto{d} \flecha correcta \) Ecuación 2 (Sección de 22.5.5.1, Métrico)
ϕel cortante = Factor de diseño de cortante
F’c = Resistencia del hormigón especificada, (psi, MPa)
bw = Ancho de la zapata, (in, mm)
d = Distancia desde la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal, (in, mm)
La demanda de corte y la capacidad de corte deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de ACI 318-14:
\(\texto{V }_ _{\texto{tu}} \leq phi text{V }_ _{\texto{c}} \flecha correcta \) Ecuación 3 (ACI Eq. 7.5.1.1(b))
Módulo de diseño de la Fundación SkyCiv, de acuerdo con la Ecuación 3, calcula la relación de utilidad de corte unidireccional (Ecuación 4) tomando demanda de corte sobre la capacidad de corte.
\( \texto{Relación de utilidad} = frac{\texto{Demanda de corte}}{\texto{Capacidad de corte}} \flecha correcta \) Ecuación 4
Cizalla bidireccional
El estado límite de corte bidireccional, También conocida como punzonadora., extiende su sección crítica a una distancia “d / 2” desde la cara de la columna y alrededor del perímetro de la columna (Figura 2).
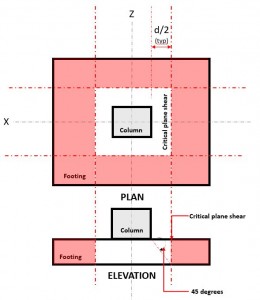
Figura 2. Plano crítico de corte de corte bidireccional
El Dos caminosescuchar demanda o V tu ocurre en el plano crítico de corte, ubicado a una distancia de “d / 2” donde el (rojo) área sombreada, indicado en la Figura 2, siguiente Sección de 22.6.4.
El Capacidad de corte o ϕVc se rige por el valor más pequeño calculado usando ecuaciones 5, 6, y 7 por Sección de 22.6.5.2
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 4 \veces lambda veces sqrt{\texto{F'}_ _{\texto{c}}} \flecha correcta \) Ecuación 5 (Sección de 22.6.5.2(a) Imperial)
\(\phi text{V }_ _{\texto{c}} = left ( 2 + \frac{4}{\beta } \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 6 (Sección de 22.6.5.2(b) Imperial)
\(\phi text{V }_ _{\texto{c}} = left ( 2 + \frac{\alfa _{s} \veces d }{b{los}} \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 7 (Sección de 22.6.5.2(c) Imperial)
o
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 0.33 \veces lambda veces sqrt{\texto{F'}_ _{\texto{c}}} \flecha correcta \) Ecuación 5 (Sección de 22.6.5.2(a) Métrico)
\(\phi text{V }_ _{\texto{c}} = 0.17 \veces left ( 1 + \frac{2}{\beta } \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 6 (Sección de 22.6.5.2(b) Métrico)
\(\phi text{V }_ _{\texto{c}} = 0.0083 \veces left ( 2 + \frac{\alfa _{s} \veces d }{b{los}} \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 7 (Sección de 22.6.5.2(c) Métrico)
Nota: β es la relación entre el lado largo y el lado corto de la columna., carga concentrada, o área de reacción y αs es dado por 22.6.5.3
λ = Factor de modificación para reflejar las propiedades mecánicas reducidas del hormigón ligero en relación con el hormigón normal de la misma resistencia a la compresión.
F’c = Resistencia del hormigón a la compresión especificada (psi, MPa)
d = Distancia desde la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal, (in, mm)
La demanda de corte y la capacidad de corte deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de ACI 318-14:
\(\texto{V }_ _{\texto{tu}} \leq phi text{V }_ _{\texto{c}} \flecha correcta \) Ecuación 8 (Sección de 7.5.1.1(b))
Módulo de diseño de la Fundación SkyCiv, de acuerdo con la Ecuación 8, calcula la relación de utilidad de corte en dos direcciones (Ecuación 9) tomando demanda de corte sobre la capacidad de corte.
\( \texto{Relación de utilidad} = frac{\texto{Demanda de corte}}{\texto{Capacidad de corte}} \flecha correcta \) Ecuación 9
Pruebas de diseño de flexión
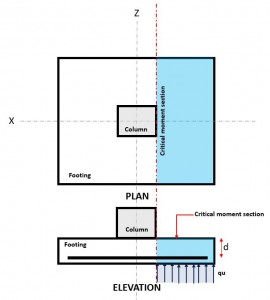
Figura 3. Sección de flexión crítica
El Flexural El estado límite se produce en la sección de flexión crítica, ubicado en la cara de la columna en la parte superior de la zapata (Figura 3).
El Demanda de flexión o Mtu se encuentra en la sección de flexión crítica (área de escotilla azul) indicado en la Figura 3, y se calcula usando la ecuación 10.
\( \texto{M}_ _{tu} = text{q}_ _{tu} \veces left ( \frac{l_{x}}{2} – \frac{C_{x}}{2} \verdad ) \veces l_{z} \veces left ( \frac{\frac{l_{x}}{2} – \frac{C_{x}}{2} }{2} \verdad ) \flecha correcta \) Ecuación 10
qtu = presión factorizada del suelo, (ksf, kPa)
lx = dimensión de pie a lo largo del eje x (in, mm)
lz = dimensión de pie a lo largo del eje z (in, mm)
cx = dimensión de la columna a lo largo del eje x (in, mm)
El Capacidad de flexión o ϕMnorte se calcula usando la ecuación 11.
\( \phi text{M}_ _{norte} = phi_{\texto{flexura}} \veces A_{s} \veces f_{y} \veces left( d – \frac{a}{2} \verdad) \flecha correcta \) Ecuación 11
ϕ = factor de diseño de flexión
lx = dimensión de pie paralela al eje x (in , mm)
lz = dimensión de pie paralela al eje z (in , mm)
d = distancia de la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal (in , mm)
As = área de refuerzo (in2 , mm2)
a = profundidad del bloque de tensión rectangular equivalente (in , mm)
fy = resistencia de refuerzo, (KSI, MPa)
La demanda de momento y la capacidad de momento deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de ACI 318-14:
\(\texto{M}_ _{\texto{tu}} \leq phi text{M}_ _{\texto{norte}} \flecha correcta \) Ecuación 12 (Sección de 7.5.1.1(b))
Módulo de diseño de la Fundación SkyCiv, de acuerdo con la Ecuación 12, calcula la relación de utilidad de flexión (Ecuación 13) tomando demanda de flexión sobre capacidad de flexión.
\( \texto{Relación de utilidad} = frac{\texto{Demanda de flexión}}{\texto{Capacidad de flexión}} \flecha correcta \) Ecuación 13
Verificaciones adicionales
Otras verificaciones no mencionadas en el código., incluyendo controles de presión del suelo, edificación, y también se verifican otros controles de estabilidad..
Presión del suelo
La determinación de la presión base o la interacción entre el suelo y la zapata depende principalmente de las dimensiones de la zapata y la excentricidad resultante de las cargas aplicadas.. Dependiendo del posicionamiento de esta excentricidad resultante, La presión de la base puede inducir una compresión total o parcial de la zapata.. Esta evaluación nos permite confirmar si el suelo subyacente puede soportar la totalidad de las cargas transmitidas desde la zapata..
Para obtener una guía detallada para calcular manualmente la presión del suelo, por favor consulte este enlace: Distribución de presión bajo una base de hormigón rectangular
El índice de utilidad se evalúa comparando la presión máxima del suelo. (estado de servicio) con la capacidad de carga bruta permitida del suelo:
\( \texto{Relación de utilidad} = frac{\texto{Max. Presión del suelo}}{\texto{Capacidad de carga bruta permitida del suelo}} \flecha correcta \) Ecuación 14
Edificación
Comprueba la carga axial gobernante que actúa sobre la zapata.. Suma todas las cargas verticales, incluida la carga del usuario y los pesos propios de la columna., losa de zapata, suelo, y fuerza de flotación. Si la columna experimenta una fuerza hacia arriba, Los pesos propios especificados deben contrarrestar la fuerza ascendente.; de lo contrario, El diseño corre el riesgo de fallar debido a la inestabilidad..
Volcarse
El vuelco de la zapata se verifica sumando todos los momentos respecto de un punto de la zapata, incluidas todas las fuerzas que actúan sobre él.. Se deben considerar todas las combinaciones de cargas de servicio para verificar el momento de vuelco gobernante.. Normalmente, un factor de seguridad de 1.5-2 Se emplea para evaluar si la zapata pasa la prueba de vuelco..
Corredizo
Para comprobar el deslizamiento, la suma de las cargas resistentes horizontales que apuntan hacia la derecha se divide por la suma de las cargas que apuntan hacia la izquierda.
- Ejemplo de cálculo del momento de vuelco:
- Fuerza horizontal debida a la fricción entre la base de la zapata y el suelo de la subestructura
- Presión pasiva del suelo (si está incluido)
- Cargas deslizantes:
- La componente horizontal de la presión activa del suelo.
- La componente horizontal de la presión resultante de la sobrecarga
Generalmente, un factor mínimo de seguridad de 1.5 se usa. Si no actúa ninguna fuerza horizontal sobre la base, No es necesario comprobar el deslizamiento..
Módulo de diseño de la Fundación SkyCiv
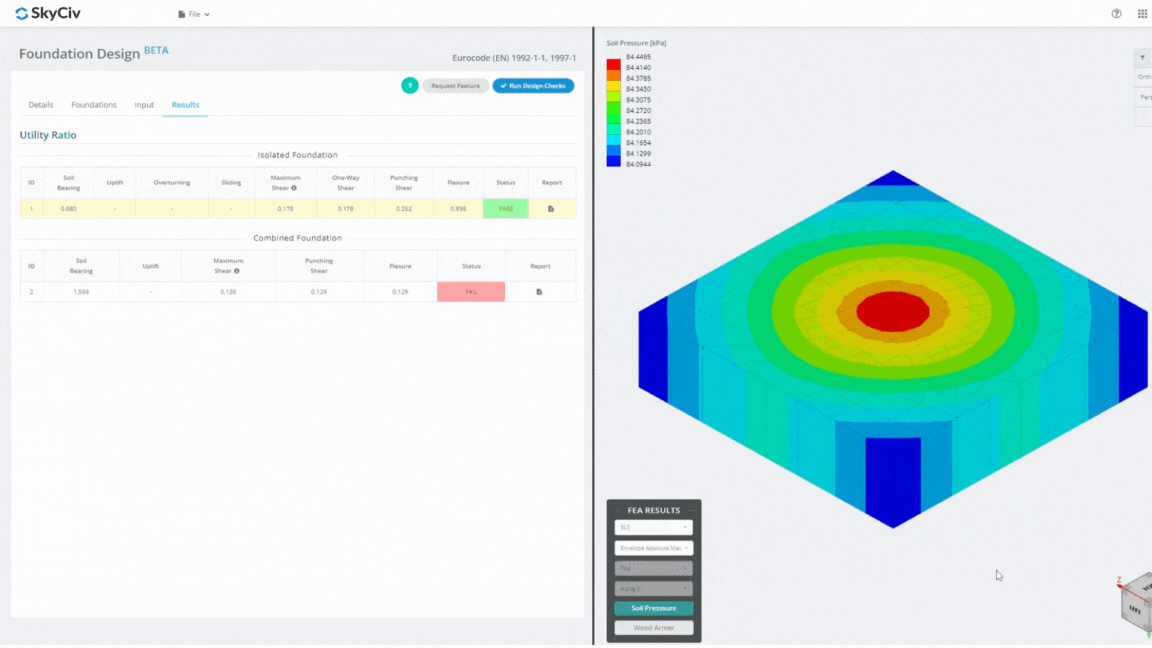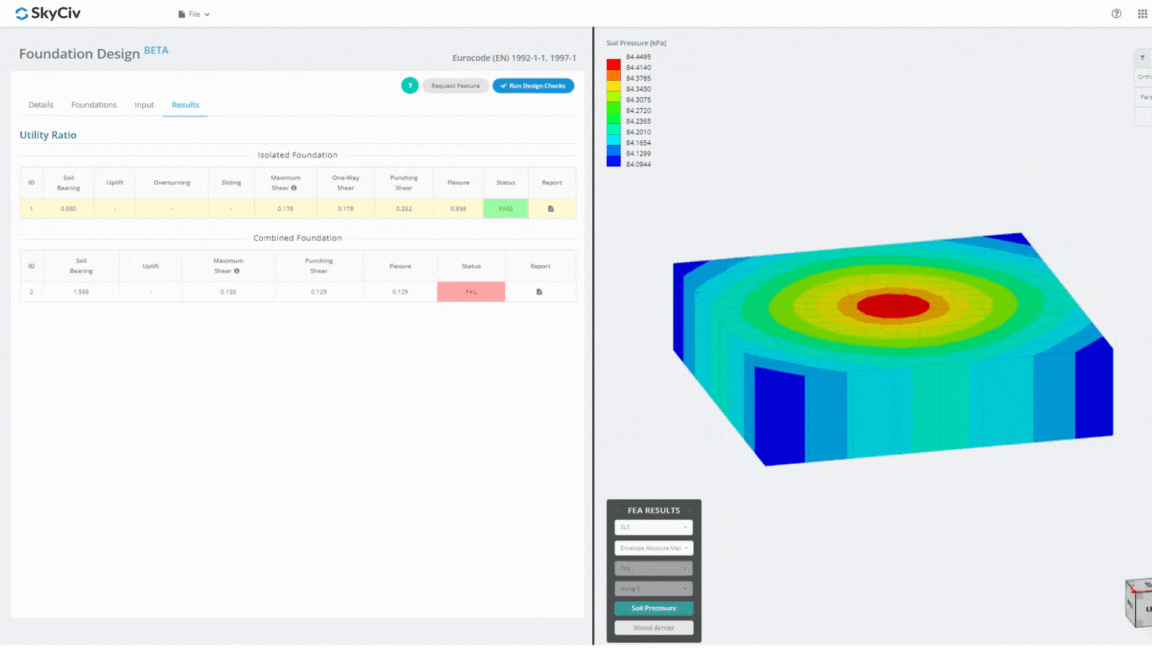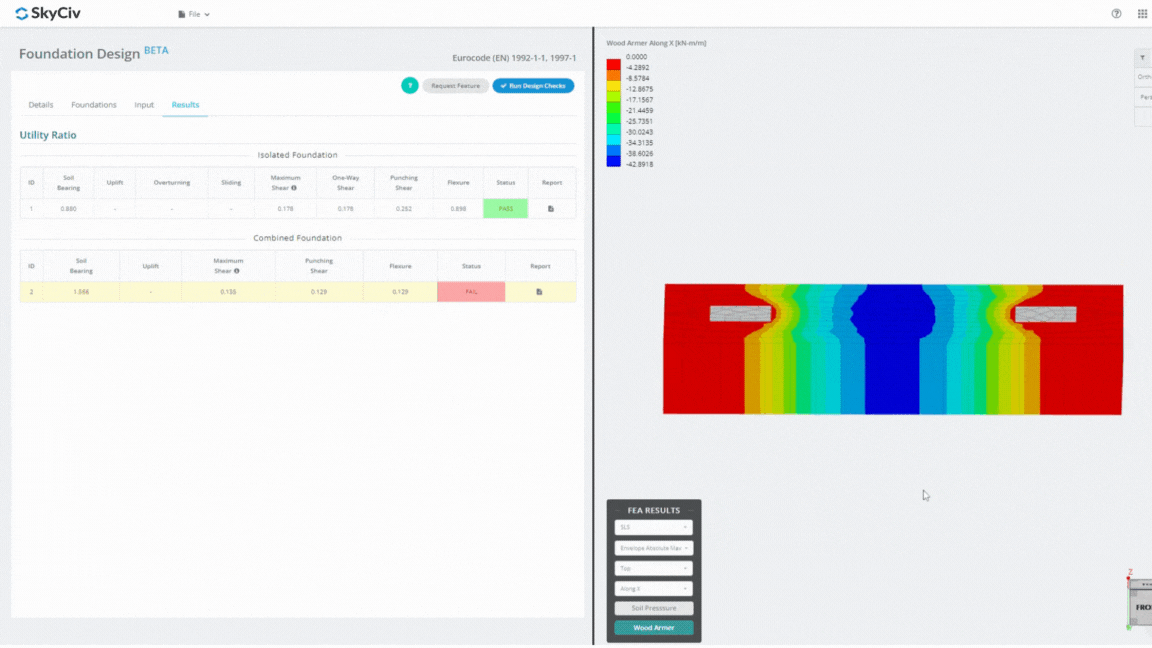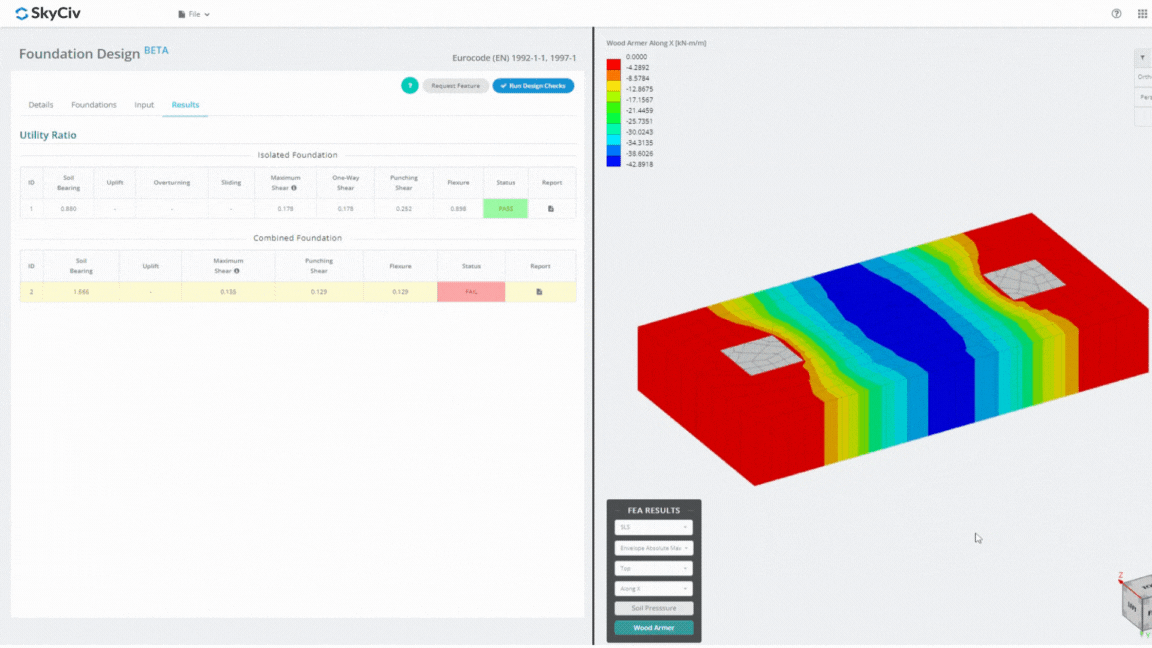
El módulo de diseño de cimientos es una poderosa herramienta integrada con el análisis de elementos finitos. (FEA), Capaz de realizar análisis exhaustivos de la presión del suelo y de la madera para realizar comprobaciones detalladas de la flexión.. Realiza todas las verificaciones estructurales especificadas por ACI. 318 y otras verificaciones mencionadas anteriormente y las presenta en un informe completo.
Comience con la Fundación SkyCiv hoy!
Inicie el Diseño de Cimientos y pruébalo hoy! Es fácil comenzar, pero si necesita más ayuda, entonces asegúrese de visitar nuestro documentación o ponte en contacto con nosotros!
No es un usuario de SkyCiv? Regístrese para un Gratis 14 Day Trial Para empezar!
Desarrollador de producto
licenciatura (Civil), maestría (Civil)
Albert Pamonag
Ingeniero estructural, Desarrollo de Producto
= ancho de la zapata. Ingeniero civil
Referencias
- Requisitos del Código de Construcción para Hormigón Estructural (ACI 318-14) Comentario sobre los requisitos del código de construcción para hormigón estructural (ACI 318R-14). Instituto Americano del Concreto, 2014.
- McCormac, Jack C., y Russell H. marrón. Diseño de hormigón armado ACI 318-11 Edición de código. Wiley, 2014.
- Taylor, Andrés, et al. El manual de diseño de hormigón armado: un compañero a ACI-318-14. Instituto Americano del Concreto, 2015.




