A Pie combinado es una base única que soporta dos o más columnas. Las zapatas combinadas se usan comúnmente cuando las columnas están demasiado espaciadas, donde dos zapatas aisladas serían insatisfactorias. Por ejemplo, con dos zapatas aisladas que están demasiado cerca una de la otra, el suelo debajo puede compartir porciones de zonas de influencia, conduciendo a una extensión requerida de una o ambas zapatas aisladas. Dependiendo de limitaciones físicas o de otro tipo, esto puede no ser posible.
El módulo SkyCiv Foundation Design incluye el diseño de zapatas combinadas de conformidad con el American Concrete Institute (ACI 318).
¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta gratuita permite a los usuarios realizar cálculos de transporte de carga sin ninguna descarga o instalación.!
Diseño de una base combinada
Requisitos de dimensión
Para determinar las dimensiones de una zapata aislada, servicio o cargas no factorizadas, como muerto (re), En Vivo (L), Viento (W), Sísmico (E), etc. se aplicará utilizando combinaciones de carga, según lo definido por ACI 318-14. Cualquier combinación de carga que gobierne se considerará la carga de diseño, y se compara con la presión de suelo permitida como se muestra en la ecuación 1, como se recomienda en Sección de 13.2.6 de ACI 318-14.
\(\texto{q}_ _{\texto{a}} = frac{ \texto{P1}_ _{\texto{norte}} + \texto{P2}_ _{\texto{norte}} }{\texto{A}} \flecha correcta \) Ecuación 1
dónde:
qa = presión neta admisible del suelo
P1norte = cargas no factorizadas en la columna 1 (izquierda)
P2norte = cargas no factorizadas en la columna 2 (verdad)
A = área de cimentación
A partir de la Ecuación 1, qa son intercambio con A.
\(\texto{A} = frac{ \texto{P1}_ _{\texto{norte}} + \texto{P2}_ _{\texto{norte}} }{\texto{q}_ _{\texto{a}}} \flecha correcta \) Ecuación 1a
En este punto, Las dimensiones de la zapata se pueden volver a calcular a partir de la dimensión del área requerida, A.
Cizalla unidireccional
El Cizalla unidireccional estado límite, también conocido como “cizalla flexural”, extiende su sección crítica a lo ancho de la zapata y se ubica a una distancia “d” de la cara de una columna, donde se encuentra la cizalladura del plano crítico (Consulte la figura 1).
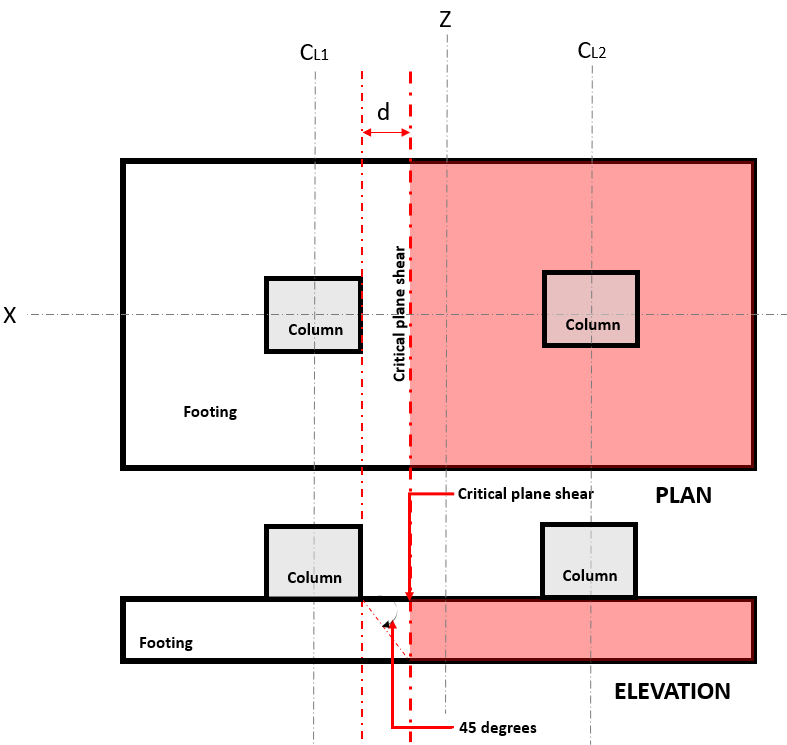
Figura 1. Corte en plano crítico de corte unidireccional
El De una sola mano Corte Demanda o V tu se calcula asumiendo que la base está en voladizo lejos de la columna donde está el área (rojo) indicado en la Figura 1 de acuerdo con ACI 318-14, Sección de 8.5.3.1.1.
El Capacidad de corte unidireccional o ϕVc se define como la resistencia al corte máxima y se calcula utilizando la ecuación 2 por ACI 318-14, Sección de 22.5.5.1:
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 2 \sqrt{\texto{F'}_ _{\texto{c}}} \tiempos texto{b}_ _{\texto{w}} \tiempos texto{d} \flecha correcta \) Ecuación 2 (ACI Eq. 22.5.5.1 Inglés)
o
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 0.17 \sqrt{\texto{F'}_ _{\texto{c}}} \tiempos texto{b}_ _{\texto{w}} \tiempos texto{d} \flecha correcta \) Ecuación 2 (ACI Eq. 22.5.5.1 Métrico)
dónde:
ϕel cortante = factor de diseño de corte
F’c = resistencia especificada del concreto, psi o MPa
bw = espesor de la zapata, en o mm
d = distancia de la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal, en o mm
La demanda de corte y la capacidad de corte deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de ACI 318-14:
\(\texto{V }_ _{\texto{tu}} \leq phi text{V }_ _{\texto{c}} \flecha correcta \) Ecuación 3 (ACI Eq. 7.5.1.1(b))
Fundación SkyCiv, en cumplimiento de la ecuación 3, calcula la relación de unidad de corte unidireccional (Ecuación 4) tomando demanda de corte sobre la capacidad de corte.
\( \texto{proporción} = frac{\texto{Demanda de corte}}{\texto{Capacidad de corte}} \flecha correcta \) Ecuación 4
Cizalla bidireccional
El Cizalla bidireccional estado límite, también conocido como “cizalla de perforación”, extiende su sección crítica a una distancia "d / 2" de la cara de la columna y alrededor del perímetro de la columna. El plano crítico de corte se encuentra en esa sección de la zapata (Consulte la figura 2).
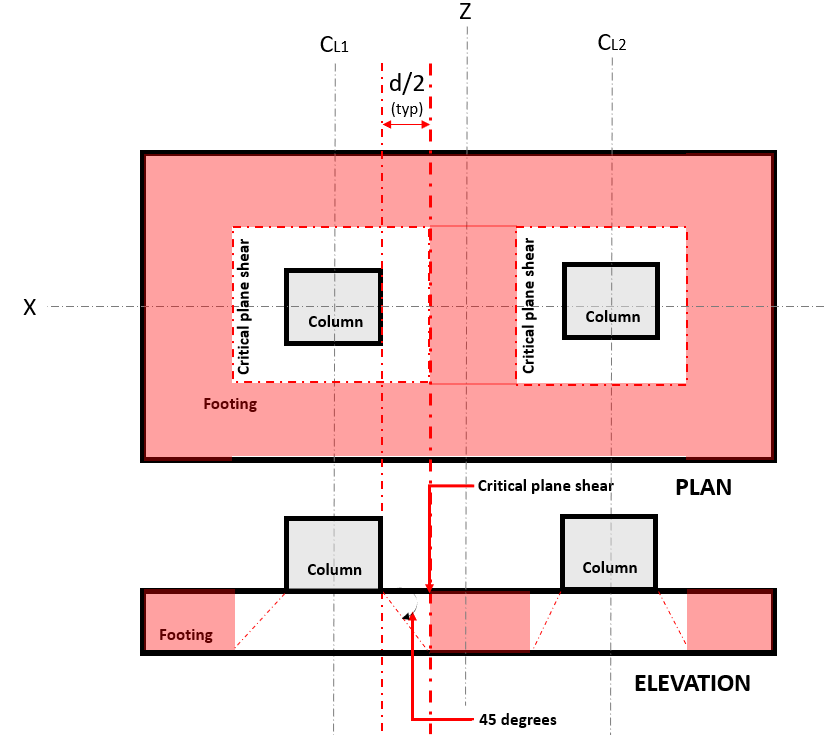
Figura 2. Corte de plano crítico de corte bidireccional
El Dos caminosescuchar demanda o V tu ocurre en el plano crítico de corte, ubicado a una distancia de "d / 2" donde el (rojo) área sombreada, indicado en la Figura 2, de acuerdo con ACI 318-14, Sección de 22.6.4.
El Capacidad de corte o ϕVc se rige por el valor más pequeño calculado usando la ecuación 5, 6, y 7 por ACI 318-14, Sección de 22.6.5.2:
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 4 \veces lambda veces sqrt{\texto{F'}_ _{\texto{c}}} \flecha correcta \) Ecuación 5 (ACI Eq. 22.6.5.2(a) Inglés)
\(\phi text{V }_ _{\texto{c}} = left ( 2 + \frac{4}{\beta } \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 6 (ACI Eq. 22.6.5.2(b) Inglés)
\(\phi text{V }_ _{\texto{c}} = left ( 2 + \frac{\alfa _{s} \veces d }{b{los}} \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 7 (ACI Eq. 22.6.5.2(c) Inglés)
o
\(\phi text{V }_ _{\texto{c}} = phi _{\texto{el cortante}} \veces 0.33 \veces lambda veces sqrt{\texto{F'}_ _{\texto{c}}} \flecha correcta \) Ecuación 5 (ACI Eq. 22.6.5.2(a) Métrico)
\(\phi text{V }_ _{\texto{c}} = 0.17 \veces left ( 1 + \frac{2}{\beta } \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 6 (ACI Eq. 22.6.5.2(b) Métrico)
\(\phi text{V }_ _{\texto{c}} = 0.0083 \veces left ( 2 + \frac{\alfa _{s} \veces d }{b{los}} \verdad ) \veces lambda veces sqrt{F'_{c}} \flecha correcta \) Ecuación 7 (ACI Eq. 22.6.5.2(c) Métrico)
Nota: β es la relación del lado largo al lado corto de la columna, carga concentrada, o área de reacción y αs es dado 22.6.5.3
dónde:
λ = factor de modificación para reflejar las propiedades mecánicas reducidas del concreto liviano en relación con el concreto de peso normal de la misma resistencia a la compresión
F’c = resistencia especificada del concreto, psi o MPa
d = distancia de la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal, pulg. o mm
La demanda de corte y la capacidad de corte deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de ACI 318-14:
\(\texto{V }_ _{\texto{tu}} \leq phi text{V }_ _{\texto{c}} \flecha correcta \) Ecuación 8 (ACI Eq. 7.5.1.1(b))
Fundación SkyCiv, en cumplimiento de la ecuación 8, calcula la relación de unidad de corte bidireccional (Ecuación 9) tomando demanda de corte sobre la capacidad de corte.
\( \texto{proporción} = frac{\texto{Demanda de corte}}{\texto{Capacidad de corte}} \flecha correcta \) Ecuación 9
Pruebas de diseño de flexión
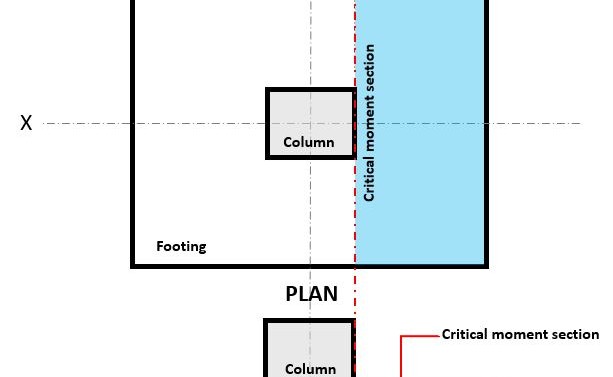
Figura 3. Sección de momento crítico de flexión
El Flexural el estado límite se produce en la sección de flexión crítica, ubicado en la cara de la columna en la parte superior de la zapata (Consulte la figura 3).
El Demanda de flexión, o Mtu se encuentra en la sección de flexión crítica (área de escotilla azul) indicado en la Figura 3, y se calcula usando la ecuación 10:
\( \texto{M}_ _{tu} = text{q}_ _{tu} \veces left ( \frac{l_{x}}{2} – \frac{C_{x}}{2} \verdad ) \veces l_{z} \veces left ( \frac{\frac{l_{x}}{2} – \frac{C_{x}}{2} }{2} \verdad ) \flecha correcta \) Ecuación 10
dónde:
qtu = presión factorizada del suelo, ksf o kpa
lx = dimensión de pie paralela al eje x, en o mm
lz = dimensión de pie paralela al eje z, en o mm
cx = dimensión de la columna paralela al eje x, en o mm
El Capacidad de flexión, o ϕMn se calcula usando la ecuación 11:
\( \phi text{M}_ _{norte} = phi_{\texto{flexura}} \veces A_{s} \veces f_{y} \veces left( d – \frac{a}{2} \verdad) \flecha correcta \) Ecuación 11
dónde:
ϕ = factor de diseño de flexión
lx = dimensión de pie paralela al eje x, en o mm
lz = dimensión de pie paralela al eje z, en o mm
d = distancia de la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal, en o mm
As = área de refuerzo, in2 o mm2
a = profundidad del bloque de tensión rectangular equivalente, en o mm
fy = resistencia del acero, ksi o MPa
La demanda de momento y la capacidad de momento deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de ACI 318-14:
\(\texto{M}_ _{\texto{tu}} \leq phi text{M}_ _{\texto{norte}} \flecha correcta \) Ecuación 12 (ACI Eq. 7.5.1.1(b))
Fundación SkyCiv, en cumplimiento de la ecuación 12, calcula la relación de unidad de flexión (Ecuación 13) tomando demanda de flexión sobre capacidad de flexión
\( \texto{proporción} = frac{\texto{Demanda de flexión}}{\texto{Capacidad de flexión}} \flecha correcta \) Ecuación 13
Albert Pamonag
Ingeniero estructural, Desarrollo de Producto
B.S. Ingeniero civil
Referencias
- Requisitos del Código de Construcción para Hormigón Estructural (ACI 318-14) Comentario sobre los requisitos del código de construcción para hormigón estructural (ACI 318R-14). Instituto Americano del Concreto, 2014.
- McCormac, Jack C., y Russell H. marrón. Diseño de hormigón armado ACI 318-11 Edición de código. Wiley, 2014.
- Taylor, Andrés, et al. El manual de diseño de hormigón armado: un compañero a ACI-318-14. Instituto Americano del Concreto, 2015.



