Ejemplo de diseño de placa base utilizando como 4100:2020 y AS 3600:2018
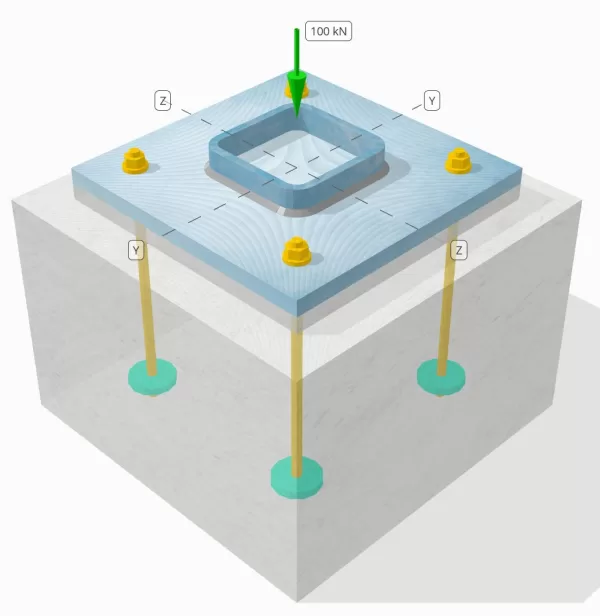
Declaración del problema:
Determine si la conexión de placa de columna a base diseñada es suficiente para una carga de compresión de 100 kn..
Datos dados:
Columna:
Sección de columna: 50×10 SHS
Área de columna: 5260 mm2
Material de columna: AS / NZS 1163 Gramo. C350
Plato base:
Dimensiones de placa base: 350 mm x 350 mm
Espesor de la placa base: 20 mm
Material de placa base: AS / NZS 3678 Gramo. C250
Lechada:
Espesor de la lechada: 20 mm
Hormigón:
Dimensiones concretas: 450 mm x 450 mm
Espesor de concreto: 300 mm
Material de hormigón: N28
Soldaduras:
Tamaño de soldadura: 6 mm
Clasificación de metal de relleno: E43xx
Carga de compresión transferida solo a través de soldaduras? SÍ
Cálculos paso a paso:
Cheque #1: Calcular la capacidad de carga de concreto
Para comenzar, Determinamos el áreas de rodamiento por AS 3600:2018 Cláusula 12.6:
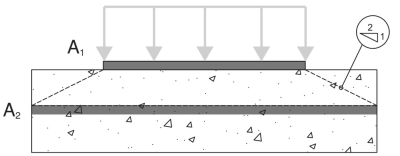
A1 - Área de rodamiento de placa base
A2 - Área de soporte de soporte de concreto, proyectado en un 2:1 Pendiente
\(
A_1 = L_{pb} SI_{pb} = 350 \, \texto{mm} \veces 350 \, \texto{mm} = 122500 \, \texto{mm}^ 2
\)
\(
A_2 = n_{A2} SI_{A2} = 450 \, \texto{mm} \veces 450 \, \texto{mm} = 202500 \, \texto{mm}^ 2
\)
Desde allí, calculamos el capacidad de carga de concreto, expresado como una fuerza equivalente. Usamos Guía de diseño de ASI 07 1S t Ed. Sección de 9.1 como referencia.
\(
\phi n_c = min izquierda( \fi 0.9 \izquierda( F’_C Derecha) A_1 sqrt{\frac{A_2}{A_1}}, \fi 1.8 \izquierda( F’_C Derecha) A_1 Derecha)
\)
\(
\phi n_c = min izquierda( 0.6 \veces 0.9 \veces left( 28 \, \texto{MPa} \verdad) \veces 122500 \, \texto{mm}^2 Times sqrt{\frac{202500 \, \texto{mm}^ 2}{122500 \, \texto{mm}^ 2}}, 0.6 \veces 1.8 \veces left( 28 \, \texto{MPa} \verdad) \veces 122500 \, \texto{mm}^2 Derecha)
\)
\(
\no -n_c = 2381.4 \, \texto{kN}
\)
Ya que 100 kN <2381.4 kN, la La capacidad de soporte de concreto es suficiente.
Cheque #2: Calcular la capacidad de soldadura
Para evaluar la capacidad de soldadura, Primero determinamos el Longitud total de soldadura Basado en las dimensiones de la columna:
\(
L_{\texto{soldar}} = 2 \izquierda( B_{\texto{columna}} – 2 r_{\texto{columna}} – 2 A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{\texto{columna}} \verdad) + 2 \izquierda( D_{\texto{columna}} – 2 r_{\texto{columna}} – 2 A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{\texto{columna}} \verdad)
\)
\(
L_{\texto{soldar}} = 2 \veces left( 150 \, \texto{mm} – 2 \veces 15 \, \texto{mm} – 2 \veces 10 \, \texto{mm} \verdad) + 2 \veces left( 150 \, \texto{mm} – 2 \veces 15 \, \texto{mm} – 2 \veces 10 \, \texto{mm} \verdad) = 400 \, \texto{mm}
\)
con esto, podemos calcular el estrés por unidad de longitud de soldadura, asumiendo el 100 La carga de KN se distribuye uniformemente:
\(
V^*_ w = frac{N_X}{L_{\texto{soldar}}} = frac{100 \, \texto{kN}}{400 \, \texto{mm}} = 0.25 \, \texto{kN / mm}
\)
Después, Determinamos el capacidad de soldadura por unidad de longitud usando AS 4100:2020 Cláusula 9.6.3.10:
\(
\Phi v_w = phi 0.6 F_{tu} E_w k_r = 0.8 \veces 0.6 \veces 430 \, \texto{MPa} \veces 4.243 \, \texto{mm} \veces 1 = 0.87576 \, \texto{kN / mm}
\)
Ya que 0.87576 kN / mm < 0.25 kN / mm, la La capacidad de soldadura es suficiente.
Cheque #3: Calcule la capacidad de rendimiento de flexión de la placa base debido a la carga de compresión
La capacidad de flexión de la placa base depende de sus dimensiones. Si el plato es demasiado ancho, Requerirá material más grueso. Seleccionar el tamaño de la placa base derecho para una carga dada requiere experiencia, y realizar múltiples cálculos puede llevar mucho tiempo. El Software de diseño de placa base de SkyCiv simplifica este proceso, habilitando modelado y análisis rápidos y eficientes en solo segundos.
Usamos Guía de diseño de ASI 07, 1Santa ed., Tabla 7 Para verificar la capacidad de rendimiento de la flexión de la placa base. primero, Determinamos el kx factor.
\(
k_x = 1.65 \izquierda( \frac{\sqrt{L_{pb} SI_{pb}}}{B_{\texto{columna}}} \verdad) = 1.65 \veces left( \frac{\sqrt{350 \, \texto{mm} \veces 350 \, \texto{mm}}}{150 \, \texto{mm}} \verdad) = 3.85
\)
próximo, Calculamos la resistencia de la carga de concreto en términos de estrés sobre el área. Referirse a Cheque #1 para la capacidad de carga calculada.
\(
\Phi f_b = frac{\no -n_c}{L_{pb} SI_{pb}} = frac{2381.4 \, \texto{kN}}{350 \, \texto{mm} \veces 350 \, \texto{mm}} = 19.44 \, \texto{MPa}
\)
Luego usamos este valor para obtener el X factor.
\(
X = frac{4 N_c^*}{\Phi F_B (2 B_{\texto{columna}})^ 2} = frac{4 \veces 100 \, \texto{kN}}{19.44 \, \texto{MPa} \veces (2 \veces 150 \, \texto{mm})^ 2} = 0.22862
\)
Ahora, Usemos el calculado kx y X factores para evaluar el λ (lambda ) factor.
\(
\lambda = min izquierda( \frac{k_x sqrt{X}}{1 + \sqrt{1 – X}}, 1.0 \verdad) = min left( \frac{3.85 \veces sqrt{0.22862}}{1 + \sqrt{1 – 0.22862}}, 1 \verdad) = 0.98008
\)
Luego calculamos la longitud del voladizo de la placa base que experimenta la carga de cojinetes. De acuerdo a Guía de diseño de ASI 07, 1Santa ed., compuestas 6.1 y 9.1–9.2, La longitud del voladizo es como se muestra:
\(
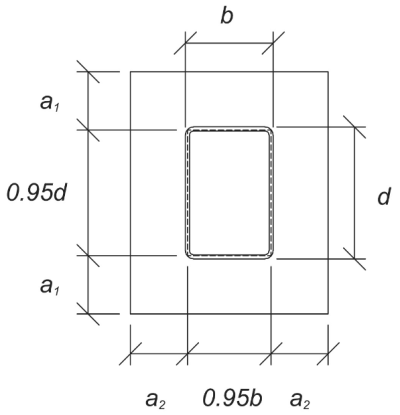
l = max izquierda( \frac{L_{pb} – 0.95 D_{\texto{columna}}}{2}, \frac{SI_{pb} – 0.95 B_{\texto{columna}}}{2}, \lambda 0.306 \sqrt{D_{\texto{columna}} B_{\texto{columna}}} \verdad)
\)
\(
l = max izquierda( \frac{350 \, \texto{mm} – 0.95 \veces 150 \, \texto{mm}}{2}, \frac{350 \, \texto{mm} – 0.95 \veces 150 \, \texto{mm}}{2}, 0.98008 \veces 0.306 \veces sqrt{150 \, \texto{mm} \veces 150 \, \texto{mm}} \verdad)
\)
\(
l = 103.75 \, \texto{mm}
\)
Considerando esta sección crítica de la placa base, Calculemos el estrés del rendimiento de flexión. Esta es una ecuación reorganizada de Guía de diseño de ASI 07, 1Santa ed., Sección de 9.2, con referencia a Sección de 6.1.
\(
f^* = frac{2 N_x l^2}{SI_{pb} L_{pb} (A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{pb})^ 2}
\)
\(
f^* = frac{2 \veces 100 \, \texto{kN} \veces 103.75 \, \texto{mm}^ 2}{350 \, \texto{mm} \veces 350 \, \texto{mm} \veces (20 \, \texto{mm})^ 2} = 43.935 \, \texto{MPa}
\)
El paso final es calcular la capacidad de rendimiento de la placa base utilizando AS 4100:2020, Cláusula 5.2.1.
\(
\Phi F_Y = Phi F_{y_{pb}} = 0.9 \veces 250 \, \texto{MPa} = 225 \, \texto{MPa}
\)
Ya que 43.935 MPa < 225 MPa, la La capacidad de flexión de la placa base es suficiente.
Resumen de diseño
El software de diseño de placa base SkyCiv puede generar automáticamente un informe de cálculo paso a paso para este ejemplo de diseño. También proporciona un resumen de los controles realizados y sus proporciones resultantes, Hacer que la información sea fácil de entender de un vistazo. A continuación se muestra una tabla de resumen de muestra, que se incluye en el informe.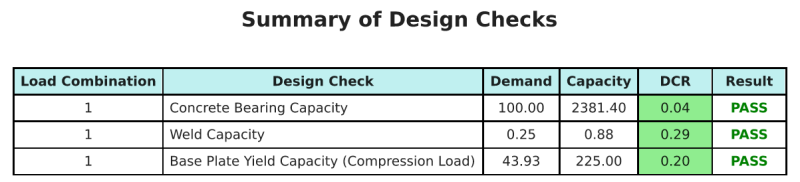
Informe de muestra de SkyCiv
haga clic aquí Para descargar un informe de muestra.
Comprar software de placa base
Compre la versión completa del módulo de diseño de la placa base por sí solo sin ningún otro módulo SkyCiv. Esto le da un conjunto completo de resultados para el diseño de placa base, incluyendo informes detallados y más funcionalidad.
