Ejemplo de diseño de placa base usando AISC 360-22 y ACI 318-19
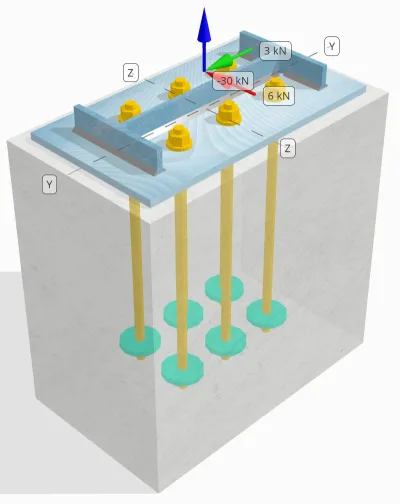
Declaración del problema
Determine si la conexión diseñada entre la columna y la placa base es suficiente para 30 carga de tensión kN, 3 kN Vy carga de corte, y 6 kN Vz carga de corte.
Datos dados
Columna:
Sección de columna: A14x30
Área de columna: 5709.7 mm2
Material de columna: A992
Plato base:
Dimensiones de placa base: 250 mm x 250 mm
Espesor de la placa base: 12 mm
Material de placa base: A992
Lechada:
Espesor de la lechada: 0 mm
Hormigón:
Dimensiones concretas: 300 mm x 500 mm
Espesor de concreto: 500 mm
Material de hormigón: 20.7 MPa
Agrietado o sin crack: Agrietado
Ancla:
Diámetro de anclaje: 16 mm
Longitud de incrustación efectiva: 400 mm
Final de ancla: Placa circular
Diámetro de placa incrustada: 70 mm
Espesor de la placa incrustada: 10 mm
Material de acero: F1554 Gr.55
Roscas en plano de corte: Incluido
Soldaduras:
Tamaño de soldadura: 7 mm
Clasificación de metal de relleno: E70XX
Aniquilar datos (de Calculadora de SkyCiv):
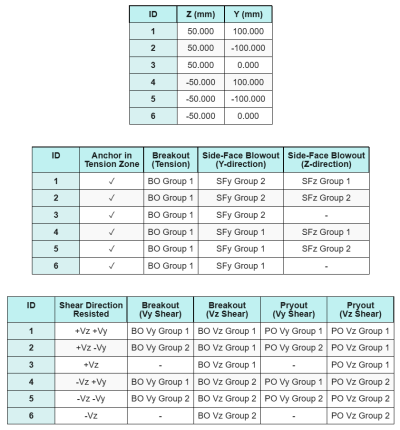
Modelo en la herramienta gratuita SkyCiv
Modele el diseño de la placa base anterior utilizando nuestra herramienta gratuita en línea hoy! No es necesario registrarse.
Nota
El propósito de este ejemplo de diseño es demostrar los cálculos paso a paso para verificaciones de capacidad que involucran cargas axiales y de corte simultáneas.. Algunas de las comprobaciones requeridas ya se han comentado en los ejemplos de diseño anteriores.. Consulte los enlaces proporcionados en cada sección..
Cálculos paso a paso
Cheque #1: Calcular la capacidad de soldadura
Para determinar la capacidad de soldadura bajo carga simultánea., Primero necesitamos calcular la demanda de soldadura debido a la carga de corte y la demanda de soldadura debido a la carga de tensión. Puedes consultar esto enlace para el procedimiento para obtener las demandas de soldadura por corte, y esto enlace para las demandas de soldadura por tensión.
Para este diseño, la demanda de soldadura en la web debido a la carga de tensión se encuentra que es el siguiente, donde el estrés se expresa como fuerza por unidad de longitud.
\(r_{tu,\texto{web}} = frac{T_{tu,\texto{ancla}}}{l_{\texto{efecto}}} = frac{5\ \texto{kN}}{93.142\ \texto{mm}} = 0.053681\ \texto{kN / mm}\)
además, la tensión de soldadura en cualquier parte de la sección de la columna debido a la carga de corte se determina como:
\(A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{uy} = frac{V_Y}{L_{\texto{soldar}}} = frac{3\ \texto{kN}}{1250.7\ \texto{mm}} = 0.0023987\ \texto{kN / mm}\)
\(A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{a} = frac{V_Z}{L_{\texto{soldar}}} = frac{6\ \texto{kN}}{1250.7\ \texto{mm}} = 0.0047973\ \texto{kN / mm}\)
Dado que existe una combinación de cargas de tensión y de corte en el web, necesitamos obtener la resultante. Expresando esto como fuerza por unidad de longitud, tenemos:
\(r_u = sqrt{(r_{tu,\texto{web}})^ 2 + (A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{uy})^ 2 + (A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{a})^ 2}\)
\(r_u = sqrt{(0.053681\ \texto{kN / mm})^ 2 + (0.0023987\ \texto{kN / mm})^ 2 + (0.0047973\ \texto{kN / mm})^ 2}\)
\(r_u = 0.053949\ \texto{kN / mm}\)
Para el bridas, sólo están presentes tensiones cortantes. Así, el resultante es:
\(r_u = sqrt{(A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{uy})^ 2 + (A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{a})^ 2}\)
\(r_u = sqrt{(0.0023987\ \texto{kN / mm})^ 2 + (0.0047973\ \texto{kN / mm})^ 2} = 0.0053636\ \texto{kN / mm}\)
próximo, calculamos el capacidades de soldadura. para la brida, determinamos el ángulo θ utilizando la Vz y Vy cargas.
\( \theta = tan^{-1}\!\izquierda(\frac{A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{uy}}{A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{a}}\verdad) = tan^{-1}\!\izquierda(\frac{0.0023987\ \texto{kN / mm}}{0.0047973\ \texto{kN / mm}}\verdad) = 0.46365\ \texto{trabajo} \)
Por consiguiente, la kds El factor y la capacidad de soldadura se calculan utilizando AISC 360-22 Eq. J2-5 y Eq. J2-4.
\(Suma de fuerzas de tensión de anclajes con área de cono de ruptura de concreto común{ds} = 1.0 + 0.5(\sin(\theta))^{1.5} = 1 + 0.5 \veces (\sin(0.46365\ \texto{trabajo}))^{1.5} = 1.1495\)
\(\Phi R_{norte,flg} = phi,0.6,F_{Exx}\,E_w,k_{ds} = 0.75 \veces 0.6 \veces 480\ \texto{MPa} \veces 4.95\ \texto{mm} \veces 1.1495 = 1.2291\ \texto{kN / mm}\)
para la web, calculamos el angulo θ usando una fórmula diferente. Tenga en cuenta que Guau se utiliza en la fórmula ya que representa la carga paralela al eje de soldadura.
\( \theta = cos^{-1}\!\izquierda(\frac{A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{uy}}{r_u}\verdad) = cos^{-1}\!\izquierda(\frac{0.0023987\ \texto{kN / mm}}{0.053949\ \texto{kN / mm}}\verdad) = 1.5263\ \texto{trabajo} \)
Utilizando AISC 360-22 Eq. J2-5 y Eq. J2-4, la kds El factor y la capacidad de soldadura resultante se determinan de la misma manera..
\(Suma de fuerzas de tensión de anclajes con área de cono de ruptura de concreto común{ds} = 1.0 + 0.5(\sin(\theta))^{1.5} = 1 + 0.5 \veces (\sin(1.5263\ \texto{trabajo}))^{1.5} = 1.4993\)
\(\Phi R_{norte,web} = phi,0.6,F_{Exx}\,E_w,k_{ds} = 0.75 \veces 0.6 \veces 480\ \texto{MPa} \veces 4.95\ \texto{mm} \veces 1.4993 = 1.603\ \texto{kN / mm}\)
Por último, realizamos controles de metal base tanto para la columna como para la placa base, luego obtenga la capacidad del metal base gobernante.
\( \Phi R_{Nbm,columna} = phi,0.6,F_{tu,columna}\,A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{columna,medio} = 0.75 \veces 0.6 \veces 448.2\ \texto{MPa} \veces 3.429\ \texto{mm} = 0.6916\ \texto{kN / mm} \)
\( \Phi R_{Nbm,pb} = phi,0.6,F_{tu,pb}\,A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{pb} = 0.75 \veces 0.6 \veces 400\ \texto{MPa} \veces 12\ \texto{mm} = 2.1595\ \texto{kN / mm} \)
\( \Phi R_{Nbm} = mingrande(\Phi R_{Nbm,pb},\ \Phi R_{Nbm,columna}\grande) = min(2.1595\ \texto{kN / mm},\ 0.6916\ \texto{kN / mm}) = 0.6916\ \texto{kN / mm} \)
Luego comparamos el capacidades de soldadura de filete y capacidades de metales comunes para las demandas de soldadura en el bridas y alma por separado.
Ya que 0.053949 kN / mm < 0.6916 kN / mm, La capacidad de soldadura es suficiente.
Cheque #2: Calcule la capacidad de rendimiento de flexión de la placa base debido a la carga de tensión
Un ejemplo de diseño para la capacidad de fluencia a flexión de la placa base ya se analiza en el Ejemplo de diseño de placa base para tensión.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #3: Calcular la capacidad de tracción de la barra de anclaje
En el Ejemplo de diseño de placa base para tensión ya se analiza un ejemplo de diseño para la capacidad de tracción de la varilla de anclaje.. Consulte este enlace para ver el cálculo paso a paso.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #4: Calcule la capacidad de ruptura de concreto en tensión
Un ejemplo de diseño para la capacidad del concreto en ruptura por tensión ya se analiza en el Ejemplo de diseño de placa base para tensión.. Consulte este enlace para ver el cálculo paso a paso.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #5: Calcular la capacidad de extracción de anclaje
En el Ejemplo de diseño de placa base para tensión ya se analiza un ejemplo de diseño para la capacidad de extracción del anclaje.. Consulte este enlace para ver el cálculo paso a paso.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #6: Calcular la capacidad de flexión de la placa de incrustación
Un ejemplo de diseño para la verificación suplementaria de la capacidad de fluencia a flexión de la placa integrada ya se analiza en el Ejemplo de diseño de placa base para tensión.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #7: Calcule la capacidad de reventón de la cara lateral en la dirección Y
Para calcular el Reventón lateral (SFBO) capacidad, primero determinamos el total fuerza de tensión en los anclajes más cercanos al borde. Para este cheque, Evaluaremos la capacidad del borde a lo largo del dirección Y.
Dado que las proyecciones del cono de falla del SFBO a lo largo de la dirección Y se superponen, Los anclajes se tratan como un grupo de ancla.
La demanda de tensión total del grupo de anclaje se calcula como:
\(NORTE_{hacer} = left(\frac{N_X}{norte_{a,t}}\verdad) norte_{y,G1} = left(\frac{30\ \texto{kN}}{6}\verdad) \veces 3 = 15\ \texto{kN}\)
próximo, Determinamos el distancias al borde:
\(C_{z,\min} = min(C_{\texto{izquierda},G1},\ C_{\texto{verdad},G1}) = min(100\ \texto{mm},\ 200\ \texto{mm}) = 100\ \texto{mm}\)
\(C_{y,\min} = min(C_{\texto{superior},G1},\ C_{\texto{inferior},G1}) = min(150\ \texto{mm},\ 150\ \texto{mm}) = 150\ \texto{mm}\)
Usando estas distancias al borde, calculamos el capacidad del grupo de anclaje de acuerdo con ACI 318-19 Eq. (17.6.4.1).
\(NORTE_{como} = left(\frac{1 + \dfrac{C_{y,\min}}{C_{z,\min}}}{4} + \frac{s_{suma,y,G1}}{6\,C_{z,\min}}\verdad)\veces 13 \veces left(\frac{C_{z,\min}}{1\ \texto{mm}}\verdad)\veces sqrt{\frac{UNA_{brg}}{\texto{mm}^ 2}}\ \lambda_a sqrt{\frac{f_c}{\texto{MPa}}}\veces 0.001\ \texto{kN}\)
\(NORTE_{como} = left(\frac{1 + \dfrac{150\ \texto{mm}}{100\ \texto{mm}}}{4} + \frac{200\ \texto{mm}}{6\veces 100\ \texto{mm}}\verdad)\veces 13 \veces left(\frac{100\ \texto{mm}}{1\ \texto{mm}}\verdad)\veces sqrt{\frac{3647.4\ \texto{mm}^ 2}{1\ \texto{mm}^ 2}}\veces 1 \veces sqrt{\frac{20.68\ \texto{MPa}}{1\ \texto{MPa}}}\veces 0.001\ \texto{kN}\)
\(NORTE_{como} = 342.16\ \texto{kN}\)
En la ecuación original, Se aplica un factor de reducción cuando el espacio entre anclajes es menor que 6ca₁, suponiendo que los anclajes con cabeza tengan suficiente distancia al borde. sin embargo, en este ejemplo de diseño, ya que ca₂ < 3ca₁, la calculadora SkyCiv aplica un factor de reducción adicional para tener en cuenta la capacidad de borde reducida.
Finalmente, la capacidad de diseño SFBO es:
\(\phi N_{como} = fi,N_{como} = 0.7 \veces 342.16\ \texto{kN} = 239.51\ \texto{kN}\)
Ya que 15 kN < 239.51 kN, la capacidad del SFBO a lo largo de la dirección Y es suficiente.
Cheque #8: Calcule la capacidad de reventón de la cara lateral en la dirección Z
Siguiendo el mismo enfoque que en Cheque #7, la demanda de tensión total del grupo de anclaje para los anclajes más cercanos al dirección Z borde es:
\(NORTE_{hacer} = left(\frac{N_X}{norte_{a,t}}\verdad)norte_{z,G1} = left(\frac{30\ \texto{kN}}{6}\verdad)\veces 2 = 10\ \texto{kN}\)
El distancias al borde se calculan como:
\(C_{y,\min} = min(C_{\texto{superior},G1},\ C_{\texto{inferior},G1}) = min(150\ \texto{mm},\ 350\ \texto{mm}) = 150\ \texto{mm}\)
\(C_{z,\min} = min(C_{\texto{izquierda},G1},\ C_{\texto{verdad},G1}) = min(100\ \texto{mm},\ 100\ \texto{mm}) = 100\ \texto{mm}\)
El capacidad nominal SFBO luego se determina como:
\(NORTE_{como} = left(\frac{1 + \dfrac{C_{z,\min}}{C_{y,\min}}}{4} + \frac{s_{suma,z,G1}}{6\,C_{y,\min}}\verdad)\veces 13 \veces left(\frac{C_{y,\min}}{1\ \texto{mm}}\verdad)\veces sqrt{\frac{UNA_{brg}}{\texto{mm}^ 2}}\ \lambda_a sqrt{\frac{f_c}{\texto{MPa}}}\veces 0.001\ \texto{kN}\)
\(NORTE_{como} = left(\frac{1 + \dfrac{100\ \texto{mm}}{150\ \texto{mm}}}{4} + \frac{100\ \texto{mm}}{6\veces 150\ \texto{mm}}\verdad)\veces 13 \veces left(\frac{150\ \texto{mm}}{1\ \texto{mm}}\verdad)\veces sqrt{\frac{3647.4\ \texto{mm}^ 2}{1\ \texto{mm}^ 2}}\veces 1 \veces sqrt{\frac{20.68\ \texto{MPa}}{1\ \texto{MPa}}}\veces 0.001\ \texto{kN}\)
\(NORTE_{como} = 282.65\ \texto{kN}\)
Desde la distancia al borde ca₂ es todavía menos que 3ca₁, se aplica el mismo factor de reducción modificado.
Finalmente, la capacidad de diseño SFBO es:
\(\phi N_{como} = fi,N_{como} = 0.7 \veces 282.65\ \texto{kN} = 197.86\ \texto{kN}\)
Ya que 10 kN < 197.86 kN, la capacidad del SFBO a lo largo del dirección Z es suficiente.
Cheque #9: Calcular la capacidad de ruptura (Vy Shear)
Un ejemplo de diseño para la capacidad de ruptura del concreto en corte Vy ya se analiza en el Ejemplo de diseño de placa base para corte. Consulte este enlace para ver el cálculo paso a paso..
Cheque #10: Calcular la capacidad de ruptura (Cizalla de vz)
Un ejemplo de diseño para la capacidad de ruptura del concreto en corte Vy ya se analiza en el Ejemplo de diseño de placa base para corte. Consulte este enlace para ver el cálculo paso a paso..
Cheque #11: Calcular la capacidad de extracción (Vy Shear)
En el Ejemplo de diseño de placa base para corte ya se analiza un ejemplo de diseño para la capacidad del concreto contra falla por desprendimiento debido a corte Vy.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #12: Calcular la capacidad de extracción (Cizalla de vz)
En el Ejemplo de diseño de placa base para corte ya se analiza un ejemplo de diseño para la capacidad del concreto contra falla por desprendimiento debido a corte Vy.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #13: Calcular la capacidad de corte de la barra de anclaje
En el Ejemplo de diseño de placa base para corte ya se analiza un ejemplo de diseño para la capacidad de corte de la varilla de anclaje.. Consulte este enlace para ver el cálculo paso a paso..
Cheque #14: Calcular la capacidad cortante y axial de la varilla de anclaje. (AISC)
Para determinar la capacidad de la varilla de anclaje bajo cargas axiales y de corte combinadas., usamos AISC 360-22 Eq. J3-3a. en esta calculadora, la ecuación se reordena para expresar el resultado como la resistencia al corte modificada en lugar de.
El demanda de corte se define como el carga de corte por anclaje.
\(V_{hacer} =V_{hacer} = 2.5\ \texto{kN}\)
El demanda de tensión se expresa como la tensión de tracción en la barra de anclaje.
\(F_{Utah} = frac{NORTE_{hacer}}{UNA_{vara}} = frac{5\ \texto{kN}}{201.06\ \texto{mm}^ 2} = 24.868\ \texto{MPa}\)
El capacidad de corte modificada de la varilla de anclaje se calcula entonces como:
\(F'_{Nevada} = min!\izquierda(1.3\,F_{Nevada} – \izquierda(\frac{F_{Nevada}}{\Phi F_{Nuevo Testamento}}\verdad) F_{Utah},\; F_{Nevada}\verdad)\)
\(F'_{Nevada} = min!\izquierda(1.3\veces 232.69\ \texto{MPa} – \izquierda(\frac{232.69\ \texto{MPa}}{0.75\veces 387.82\ \texto{MPa}}\verdad)\veces 24.868\ \texto{MPa},\; 232.69\ \texto{MPa}\verdad) = 232.69\ \texto{MPa}\)
Luego multiplicamos esta fuerza por zona de anclaje usando AISC 360-22 Eq. J3-2.
\(\fi R_{norte,\texto{aisc}} = Phi f’_{Nevada} UNA_{\texto{vara}} = 0.75 \veces 232.69\ \texto{MPa} \veces 201.06\ \texto{mm}^2 = 35.09\ \texto{kN}\)
Ya que 2.5 kN < 35.09 kN, la capacidad de la varilla de anclaje es suficiente.
Cheque #15: Calcular controles de interacción (ACI)
Al verificar la capacidad de la varilla de anclaje bajo cargas combinadas de corte y tensión usando ACI, se aplica un enfoque diferente. Para completar, también realizamos el Comprobaciones de interacción de ACI en este cálculo, que incluyen otros controles de interacción concretos también.
Aquí están los resultados relaciones para todas las comprobaciones de tensión de ACI:
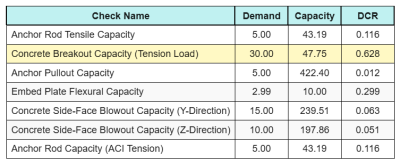
Y aquí están los resultados. relaciones para todas las comprobaciones de corte de ACI:
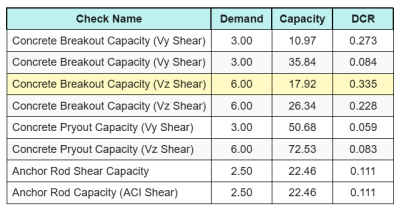
Obtenemos el cheque con la proporción más grande y lo comparamos con la proporción de interacción máxima usando ACI 318-19 Eq. 17.8.3.
\(YO_{entero} = frac{NORTE_{hacer}}{\fi n_n} + \frac{V_{hacer}}{\fi V_n} = frac{30}{47.749} + \frac{6}{17.921} = 0.96308\)
Ya que 0.96 < 1.2, la verificación de interacción es suficiente.
Resumen de diseño
El Software de diseño de placa base de SkyCiv puede generar automáticamente un informe de cálculo paso a paso para este ejemplo de diseño. También proporciona un resumen de los controles realizados y sus proporciones resultantes, Hacer que la información sea fácil de entender de un vistazo. A continuación se muestra una tabla de resumen de muestra, que se incluye en el informe.
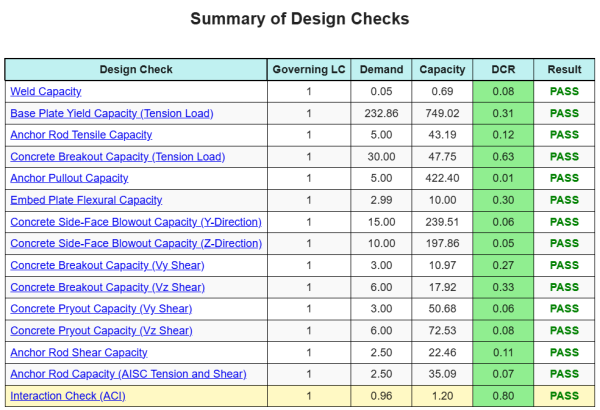
Informe de muestra de SkyCiv
Vea el nivel de detalle y claridad que puede esperar de un informe de diseño de placa base SkyCiv. El informe incluye todas las comprobaciones de diseño clave., ecuaciones, y resultados presentados en un formato claro y fácil de leer. Cumple totalmente con los estándares de diseño.. Haga clic a continuación para ver un informe de muestra generado con la calculadora de placa base SkyCiv.
Comprar software de placa base
Compre la versión completa del módulo de diseño de la placa base por sí solo sin ningún otro módulo SkyCiv. Esto le da un conjunto completo de resultados para el diseño de placa base, incluyendo informes detallados y más funcionalidad.


