Diseño de un solo pilote según AS 2159 (2009) & 3600 (2018)
En caso de carga lateral elevada o condiciones de suelo desfavorables, Los cimientos de pilotes son más preferidos a los cimientos poco profundos.. Se pueden realizar intentos tales como métodos de modificación del suelo para evitar las pilas, sin embargo, estos métodos pueden implicar procesos costosos, en donde este caso, pilas tal vez incluso más baratas.
El módulo de Diseño de la Fundación SkyCiv incluye el diseño de pilotes conforme al Instituto Americano del Concreto (ACI 318) y estándares australianos (AS 2159 & 3600).
SkyCiv's Software de diseño de estructuras de hormigón facilita la aplicación de AS 2159 y 3600 controles en proyectos estructurales.
¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta gratuita permite a los usuarios realizar cálculos de transporte de carga sin ninguna descarga o instalación.!
Diseño de resistencia geotécnica de un pilote.
Las cargas verticales aplicadas sobre los pilotes son soportadas por el soporte del extremo del pilote y la piel o la fricción del eje a lo largo de su longitud. La fuerza geotécnica del diseño (Rd,gramo) es igual a la máxima resistencia geotécnica (Rd,y) multiplicado por un factor de reducción geotécnica (øgramo) como se especifica en AS 2159 Sección de 4.3.1.
\({R}_ _{d,gramo} = {ø}_ _{gramo} × {R}_ _{d,y}\) (1)
Rd,gramo = Diseño de resistencia geotécnica
Rd,y = Máxima resistencia geotécnica
øgramo = Factor de reducción geotécnica
Máxima resistencia geotécnica (Rd,y)
La resistencia geotécnica última es igual a la suma de la fricción superficial factorizada del pilote (Fm,s ) multiplicado por el área de la superficie lateral y la resistencia de la base multiplicado por el área de la sección transversal en la punta del pilote.
\( {R}_ _{d,y} = [{R}_ _{s} × ({F}_ _{m,s} × {A}_ _{s} )] + ({F}_ _{b} × {A}_ _{b} )\) (2)
Rs = Factor de reducción de la resistencia del eje
Fm,s = Resistencia a la fricción del eje
As = Superficie lateral
Fb = Término de resistencia base
Ab = Área de la sección transversal en la punta del pilote
Para una guía más detallada, consulte nuestro artículo sobre el cálculo la resistencia a la fricción de la piel y la capacidad de carga final.
Factor de reducción geotécnica (øgramo)
El factor de reducción geotécnica es un cálculo basado en el riesgo para el diseño final que tiene en cuenta diferentes factores., como las condiciones del sitio, diseño de pila, y factores de instalación. Su valor oscila comúnmente entre 0.40 a 0.90. AS 2159 4.3.1 también establece cómo estimar su valor como se muestra en la ecuación (3).
\( {ø}_ _{gramo} = {ø}_ _{gb} + [K × ({ø}_ _{tf} – {ø}_ _{gb})] ≥ {ø}_ _{gb} \) (3)
øgb = Factor de reducción de resistencia geotécnica básica
øtf = Factor de prueba intrínseco
K = Factor de beneficio de la prueba
Las pruebas intrínsecas y los factores de beneficio de las pruebas dependen del tipo de prueba de carga utilizada en los pilotes.. Sus valores se especifican en la tabla 1 y en ecuaciones (4) y (5). La prueba de carga de pilotes se analiza brevemente en la sección 8 de AS 2159.
| Factor de prueba intrínseco (øtf) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prueba de carga estática | 0.90 | ||||||||||||
| Prueba de carga rápida | 0.75 | ||||||||||||
| Ensayo de carga dinámica de pilotes preformados | 0.80 | ||||||||||||
| Ensayo de carga dinámica de pilotes distintos de los preformados | 0.75 | ||||||||||||
| Prueba de carga bidireccional | 0.85 | ||||||||||||
| Sin pruebas | 0.80 | ||||||||||||
Tabla 1: Valores de los factores de prueba intrínsecos
Prueba del factor de beneficio para pruebas de carga estática:
\( K = frac{1.33 × p}{pag + 3.3} ≤ 1\) (4)
Prueba de factor de beneficio para pruebas de carga dinámica:
\( K = frac{1.13 × p}{pag + 3.3} ≤ 1\) (5)
p = Porcentaje del total de pilotes que se prueban y cumplen los criterios de aceptación
El factor de reducción de la resistencia geotécnica básica se evalúa utilizando un procedimiento de evaluación de riesgos discutido en la Sección 4.3. de AS 2159. El resultado de dicho procedimiento es la Calificación de Riesgo Individual (TIR) y una calificación de riesgo promedio de diseño general (ARR) que se utilizará para determinar el valor de øgb como se muestra en la Tabla 2.
| Factor de reducción de resistencia geotécnica básica (øgb) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calificación de riesgo promedio (ARR) | Categoría de Riesgo | øgb para sistemas de baja redundancia | øgb para sistemas de alta redundancia | ||||||||||
| ARR ≤ 1.5 | Muy bajo | 0.67 | 0.76 | ||||||||||
| 1.5 < ARR ≤ 2.0 | Muy bajo a bajo | 0.61 | 0.70 | ||||||||||
| 2.0 < ARR ≤ 2.5 | Bajo | 0.56 | 0.64 | ||||||||||
| 2.5 < ARR ≤ 3.0 | Bajo a moderado | 0.52 | 0.60 | ||||||||||
| 3.0 < ARR ≤ 3.5 | Moderar | 0.48 | 0.56 | ||||||||||
| 3.5 < ARR ≤ 4.0 | Moderado a alto | 0.45 | 0.53 | ||||||||||
| 4.0 < ARR ≤ 4.5 | Alto | 0.42 | 0.50 | ||||||||||
| ARR > 4.5 | Muy alto | 0.40 | 0.47 | ||||||||||
Tabla 2: Valores del factor de reducción geotécnico básico, (AS 2159 Tabla 4.3.2)
Los sistemas de baja redundancia son pilotes individuales muy cargados, mientras que los sistemas de alta redundancia incluyen grupos de pilotes grandes debajo de tapas de pilotes grandes o grupos de pilotes con más de 4 pilotes.
Resistencia estructural de diseño
Los pilotes tienen un diseño estructural casi igual que una columna. Diseño de resistencia estructural (Rd,s) requiere capacidades máximas, como fuerzas axiales y cortantes, y momento flector. La resistencia estructural de diseño de un pilote de hormigón es equivalente a la resistencia máxima de diseño. (Rnos) reducido por un factor de reducción de fuerza (øs) y un factor de colocación de hormigón (k), como se indica en la Sección 5.2.1 de AS 2159.
\( {R}_ _{d,s} = {ø}_ _{s} × k × {R}_ _{nos} \) (6)
øs = Factor de reducción de fuerza
k = factor de colocación de hormigón
Rnos = Máxima resistencia de diseño
Los valores para el factor de reducción de resistencia se muestran en la Tabla 3. El factor de colocación del hormigón oscila entre 0.75 a 1.0, dependiendo del método de construcción del pilote. sin embargo, para pilas que no sean de hormigón y lechada, k se tomará como 1.0.
| Factores de reducción de fuerza (ø) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fuerza axial sin flexión | 0.65 | ||||||||||||
| Doblado sin fuerza axial (øpb) | 0.65 ≤ 1.24 – [(13 × kuo)/12] ≤ 0.85 | ||||||||||||
| Doblado con compresión axial: | |||||||||||||
| (i) nortetu ≥ Nub | 0.60 | ||||||||||||
| (ii) nortetu < norteub | 0.60 + {(øpb – 0.66) × [1 – (nortetu/norteub)]} | ||||||||||||
| Corte | 0.70 | ||||||||||||
Tabla 3: Factores de reducción de fuerza (Tabla 2.2.2, AS 3600-18)
Capacidades axiales y de flexión de un solo pilote
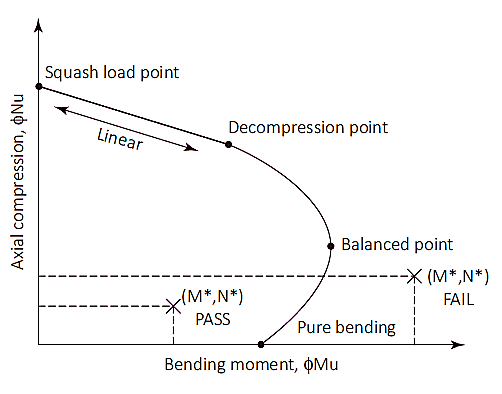
Similar a las columnas, Los pilotes también pueden estar sujetos a una carga combinada de compresión y flexión.. Las capacidades axiales y de flexión se verifican mediante un diagrama de interacción. Este diagrama es una representación visual del comportamiento de las capacidades axiales y de flexión provocadas por un aumento de la carga desde el punto de flexión puro hasta alcanzar un punto de equilibrio..
Figura 1: Diagrama de interacción de columnas
Carga de Squash (norteuo)
El punto de carga de aplastamiento es un punto en el diagrama donde el pilote fallará por compresión pura.. En este punto, la carga axial se aplica sobre el centroide plástico de la sección para permanecer en compresión sin doblarse. Carga de calabaza (norteuo) y la ubicación del centroide plástico (dq) se calculan como se muestra en las ecuaciones (7) & (8). Aunque la ubicación del centroide de plástico puede tomarse como 1/2 de la profundidad total de la sección transversal para secciones simétricas con disposición de armaduras simétricas.
\( {ϕN}_ _{uo} = ø × [({A}_ _{gramo} – {A}_ _{s}) × ({una}_ _{1} × f'c) + ({A}_ _{s} × {F}_ _{su})] \) (7)
Agramo = Área de sección transversal bruta
As = Superficie total de acero
una1 = 1.0 – (0.003 × f'c) [0.72 ≤α1 ≤0,85]
f’c = Resistencia del hormigón
Fsu = Límite elástico del acero
\( {d}_ _{q} = frac{[(b × D) – {A}_ _{s}] × ({una}_ _{1} × f'c) × sum_{i = 1}^{norte} ({A}_ _{con un} × {F}_ _{su} × {d}_ _{yi})}{{norte}_ _{uo}} \) (8)
b = Ancho de la sección transversal del pilote
D = Profundidad o diámetro de la sección transversal del pilote
Acon un = Área de la barra de refuerzo considerada
dyi = Se considera la profundidad de la barra de refuerzo
Punto de carga de aplastamiento hasta el punto de descompresión
El punto de descompresión es donde la deformación del hormigón en la fibra de compresión extrema es igual a 0.003 y la deformación en la fibra de tracción extrema es cero. La resistencia del pilote entre la carga de aplastamiento y los puntos de descompresión se puede calcular mediante interpolación lineal con factor de reducción de resistencia. (øs) de 0.6.
Punto de descompresión hasta flexión pura
El punto de flexión puro es donde la capacidad de carga axial es cero.. La transición del punto de descompresión a la flexión pura utiliza un factor de reducción de resistencia de 0.6 a 0.8 y un parámetro de entrada (ktu) es presentado. El valor de ktu empieza a 1 en el punto de descompresión y disminuye hasta que se alcanza la flexión pura. Entre la transición de los dos puntos, se logra una condición equilibrada. En este punto, la deformación del hormigón está en su límite (mic= 0,003) y la deformación del acero exterior alcanza el rendimiento (mis= 0,0025), El valor de ktu en este punto es aproximadamente 0.54 con un factor de reducción de resistencia de 0.6.
Una vez que un valor de ktu está seleccionado, Se pueden calcular las fuerzas de tracción y compresión de la sección.. La carga axial en la sección es equivalente a la suma de las fuerzas de tracción y compresión., mientras que el momento flector se calcula resolviendo estas fuerzas sobre el eje neutro. Los cálculos de las fuerzas de compresión y tracción se enumeran a continuación.
Fuerza debida al hormigón (Fcc):
\( {F}_ _{cc} = {una}_ _{2} × f'c × {A}_ _{c} \) (9)
una2 = 0.85 – (0.0015 × f'c) [una2 ≥0.67]
Ac = Área del bloque de compresión (consulte la figura 2)
= b × γ × ktu × d (sección transversal rectangular)
=(1/2) × (θ – pecado) × (D / 2)2 (sección circular)
γ = 0.97 – (0.0025 × f'c) [C ≥0.67]
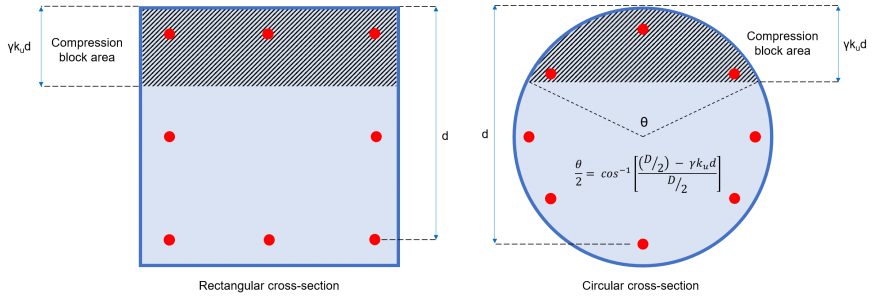
Figura 2: Área del bloque de compresión de hormigón
Fuerza (Fy) y momento (Mi) contribuido por cada barra individual:
Cada barra de refuerzo de la sección ejerce una fuerza que puede ser de compresión o tracción., dependiendo de la deformación de la barra de valor (miy) se muestra en la ecuación (10).
\( {mi}_ _{y} = frac{{mi}_ _{c}}{({k}_ _{tu} × d)} × [({k}_ _{tu} × d) – {d}_ _{yi}] \) (10)
dyi = Profundidad a la barra considerada
mic= Deformación del hormigón = 0.003
Si εy < 0 (la barra está en tensión)
Si εy > 0 (la barra está en compresión)
Barra en compresión:
\( {F}_ _{y} = {σ}_ _{y} × {A}_ _{con un} \) (11)
σy = Estrés en la barra = Mínimo [(miy × Es ), Fsu]
Es = Módulo de elasticidad del acero
Acon un = Área de bar
Barra en tensión:
\( {F}_ _{y} = [{σ}_ _{y} – ({una}_ _{2} × f'c)] × {A}_ _{con un} ≥ 0\) (12)
σy = Estrés en la barra = Mínimo [(miy × Es ), –Fsu]
Es = Módulo de elasticidad del acero
Acon un = Área de bar
Momento por cada barra:
\( {M}_ _{i} = {F}_ _{y} × {d}_ _{yi} \) (13)
Capacidad axial del pilote:
\( {la isla}_ _{tu} = ø × [ {F}_ _{cc} + {Σ}_ _{i = 1}^{norte} {F}_ _{y}]\) (14)
Capacidad de flexión del pilote:
\( {dolorido}_ _{tu} = ø × [ ({norte}_ _{tu} × {d}_ _{q}) – ({F}_ _{cc} × {y}_ _{c}) – {Σ}_ _{i = 1}^{norte} {M}_ _{i}] \) (15)
Momento flector de diseño:
Sección de 7.2 especifica que los pilotes deben tener una tolerancia fuera de posición de 75 mm para el posicionamiento horizontal de los pilotes. Este requisito puede inducir un momento flector igual a la carga axial multiplicada por la excentricidad de 75 mm.. Adicionalmente, También se considerará un momento mínimo de diseño que sea equivalente a la fuerza axial multiplicada por 5% del ancho mínimo total del pilote. Por lo tanto, el momento flector de diseño debe ser el valor mayor entre las ecuaciones 16a y 16b.
\( {M}_ _{d} = {{M}^{*}}_ _{aplicado} + ({norte}^{*} × 0.075 m) \) (16a)
\( {M}_ _{d} = {norte}^{*} × (0.05 × D) \) (16b)
Md = Momento flector de diseño
METRO*aplicado = Momento aplicado
N * = carga axial
D = ancho de la pila
Capacidad de corte de un solo pilote
El cálculo de la resistencia a cortante debe estar de acuerdo con la Sección 8.2 de AS 3600. La resistencia al corte es equivalente a las capacidades de corte combinadas del hormigón y el refuerzo de acero. (ecuación 17).
\( {Práctica}_ _{tu} = ø × ({V }_ _{uc} + {V }_ _{nos}) ≤ {Práctica}_ _{tu,max} \) (17)
Resistencia al corte del hormigón (V uc)
La contribución del hormigón a la capacidad de corte se calcula como se muestra en la ecuación (18) que se define en la sección 8.2.4.1 de AS 3600. Esta sección también requiere que el valor de √f’c no exceda 9.0 MPa. Los valores del parámetro kv y θv se determinan utilizando un método simplificado sugerido por la Sección 8.2.4.3 de AS 3600.
\( {V }_ _{uc} = {k}_ _{v} × b × {d}_ _{v} × sqrt{f'c} \) (18)
dv = Profundidad de corte efectiva = Máximo [(0.72 × D ), (0.90 × d )]
Determinación del área mínima de refuerzo a cortante. (Asv.min) & kv:
El área del refuerzo de cortante (Asv) es el área total de la barra de todas las barras de acero proporcionadas atadas en la misma dirección de la carga aplicada. Sección de 8.2.1.7 de AS 3600 proporcionó la ecuación para los refuerzos mínimos de cortante transversal, cual sera:
\( \frac{{A}_ _{sv.min}}{s} = frac{0.08 × sqrt{f'c} × b}{{F}_ _{sy.f}} \)
Fsy.f = Límite elástico de las barras de refuerzo a cortante
s = Espacio de centro a centro de las barras de refuerzo de cortante
Por (Asv/s) < (Asv.min/s):
\( {k}_ _{v} = frac{200}{[1000 + (1.3 × {d}_ _{v} )]} ≤ 0.10\)
Por (Asv/s) ≥ (Asv.min/s):
\( {k}_ _{v} = 0.15 \)
Resistencia al corte de barras de acero (V nos)
La contribución de las armaduras de cortante transversal a la capacidad de cortante calculada se muestra en la ecuación (19), que se define en la sección 8.2.5 de AS 3600.
\( {V }_ _{nos} = frac{{A}_ _{sv} × {F}_ _{sy.f} × {d}_ _{v}}{s} × cuna{θ}_ _{v} \) (19)
θv= ángulo de inclinación del puntal de compresión = 36º
Resistencia máxima al corte (V u.max)
La capacidad de corte es limitada y en ningún caso excederá el valor máximo especificado en la Sección 8.2.6 de AS 3600 (ecuación 20).
\( {V }_ _{u.max} = 0.55 × [ (f'c × b × {d}_ _{v}) × frac{cuna{θ}_ _{v} + cuna{una}_ _{v}}{1 + cuna ^{2}{θ}_ _{v} }] \) (20)
unav= ángulo entre la armadura de cortante inclinada y la armadura de tracción longitudinal≈ 90º
Máxima resistencia al corte (V tu)
La resistencia total a cortante aportada por el hormigón y los refuerzos de cortante será menor o igual al valor límite de Vu.max
\( {V }_ _{tu} = ({V }_ _{uc} + {V }_ _{nos} ) ≤ {V }_ _{u.max} \) (21)
Diseño de resistencia al corte (Prácticatu)
El factor de reducción de capacidad que se aplicará para la resistencia máxima al corte es ø = 0.7. Por lo tanto, la resistencia al corte de diseño del pilote viene dada por:
\( {Práctica}_ _{tu} = ø × ({V }_ _{uc} + {V }_ _{nos} ) \) (22)
Referencias
- Paquete, Lonnie (2018). Guía australiana para ingenieros estructurales. Prensa CRC.
- Diseño e instalación de pilotes (2009). AS 2159. Estándar australiano
- Estructuras de Hormigón (2018). AS 3600. Estándar australiano