Diseño de una sola pila de acuerdo con ACI 318 (2014)

Los pilotes son elementos largos y delgados que transfieren las cargas de la superestructura a un suelo más profundo o sobre una roca con la capacidad de carga adecuada.. Los materiales utilizados para las pilas pueden incluir madera., viga en Acero, y concreto. La instalación del pilote en el suelo se puede hincar., perforado, o gatos que luego se conectan a los pilotes. Muchos factores, como las condiciones del sitio, tipo de suelo, la transmisión de cargas, se consideran para clasificar el tipo e instalación de pilotes. Este artículo se centrará en el diseño de un pilote de hormigón de acuerdo con el American Concrete Institute. (ACI) 318 – 2014.

El módulo de Diseño de la Fundación SkyCiv incluye el diseño de pilotes conforme al Instituto Americano del Concreto (ACI 318) y estándares australianos (AS 2159 & 3600).

¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta gratuita permite a los usuarios realizar cálculos de transporte de carga sin ninguna descarga o instalación.!

Calculadora de diseño de cimientos

Capacidad de carga de una pila

Generalmente, las cargas verticales aplicadas sobre los pilotes son soportadas por el soporte del extremo del pilote, y la resistencia a la fricción de la piel desarrollada a lo largo de su longitud. La máxima capacidad de carga (Q_U) estará representado por la ecuación (1). Se aplica un factor de seguridad para calcular la capacidad de carga permitida. (Q_A).

\({Q}_ _{tu} = {Q}_ _{pag} + {Q}_ _{s}\) (1)

Q_U = Capacidad de carga máxima

Q_PAG = Resistencia del cojinete de extremo

Q_S = Resistencia a la fricción de la piel

\({Q}_ _{A} = frac{{Q}_ _{U}}{FOS} \) (2)

Q_A = Capacidad de carga permitida

FOS = Factor de seguridad

Para una guía más detallada, consulte nuestro artículo sobre el cálculo la resistencia a la fricción de la piel y la capacidad de carga final.

Resistencia estructural de un solo pilote

Los pilotes también están sujetos a fuerzas axiales, fuerza de cortante, y momento flector, razón por la cual están diseñados estructuralmente de manera similar a las columnas. Sección de 10.5.1.1 establece que toda carga factorizada no debe exceder sus correspondientes resistencias de diseño.

\( {Op}_ _{norte} ≤ {PAG}_ _{U} \) (3a)

\( {dolorido}_ _{norte} ≤ {M}_ _{U} \) (3b)

\( {Práctica}_ _{norte} ≤ {V }_ _{U} \) (3c)

PAG_U, M_U, V _U = Axial factorizado, momento flector, cargas de corte

PAG_norte, M_norte, V _norte = Axial nominal, momento flector, cargas de corte

ø = Factores de reducción de fuerza (Tabla 1)

Factores de reducción de fuerza(ϕ)
Axial	0.65-0.90
Flexural	0.65-0.90
corte	0.75

Tabla 1: Factores de reducción de fuerza (Tabla 21.2.1, ACI 318-14)

Capacidad de corte de un solo pilote (Práctica_norte)

La resistencia al corte nominal debe ser equivalente a las contribuciones combinadas de las capacidades de corte del refuerzo de hormigón y acero..

Resistencia al corte del hormigón (V _c)

La contribución del hormigón a la capacidad de corte se calcula como se muestra en la ecuación (4) que se define en la sección 22.5.5.1 de ACI 318-14.

\( {V }_ _{c} = 0.17 × λ × sqrt{fc "} × b × d \) (4)

λ = Factor de modificación del hormigón = 1 (Hormigón de peso normal, Tabla 19.2.4.2)

fc’ = Resistencia del hormigón

b = Ancho o diámetro de la pila

d = 0.80 × profundidad del pilote (Sección de 22.5.2.2)

Resistencia al corte de barras de acero (V _s)

La contribución del refuerzo de cortante lateral a la capacidad de cortante se calcula como el mínimo entre ecuaciones (5) y (6).

\( {V }_ _{s} = 0.066 × sqrt{fc "} × b × d \) (5)

\( {V }_ _{s} = frac{{A}_ _{v} × {F}_ _{yt} × d }{s} \) (6)

A_V = Área de las armaduras a cortante

F_yt = Límite elástico de las barras de refuerzo al cortante

s = Espacio de centro a centro de las barras de refuerzo de cortante

Resistencia al corte nominal (Práctica_norte)

Resumiendo la salida de la ecuación 4-6 resultará en la resistencia nominal al cortante del pilote. Factor de reducción de fuerza (ø) será igual a 0.75 como se define en la tabla 22.2.1 de ACI 318-14.

\( {Práctica}_ _{norte} = ø × ({V }_ _{c} + {V }_ _{s}) ≤ {Práctica}_ _{U} \) (7)

Calculadora de diseño de cimientos

Capacidades axiales y de flexión de un solo pilote (Op_norte, dolorido_norte )

Las capacidades axiales y de flexión se verifican mediante un diagrama de interacción. Este diagrama es una representación visual del comportamiento de las capacidades axiales y de flexión provocadas por un aumento de la carga desde el punto de flexión puro hasta alcanzar un punto de equilibrio..

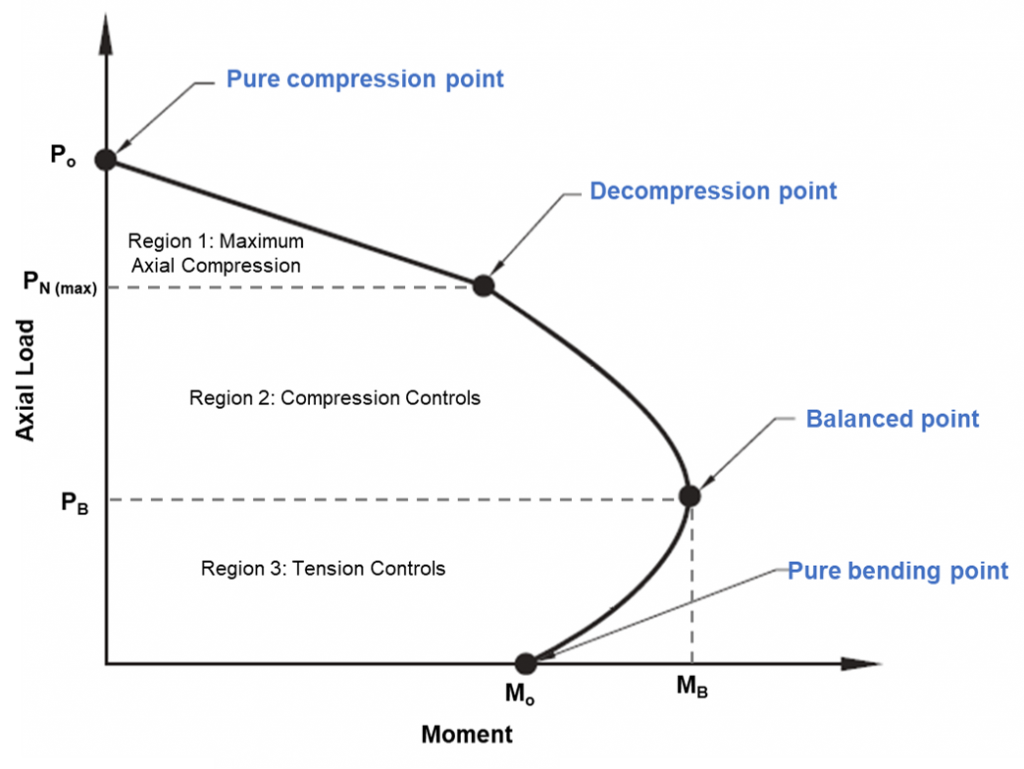
Figura 1: Diagrama de interacción de columnas

Diagrama de interacción de columnas

El punto de compresión puro en el diagrama es donde el pilote fallará la compresión puramente. En este punto, la carga axial se aplica al centroide plástico de la sección para permanecer en compresión sin doblarse. La resistencia del pilote entre el punto de compresión puro hasta los puntos de descompresión se puede calcular mediante interpolación lineal. El punto de descompresión es donde la deformación del hormigón en la fibra de compresión extrema es igual a 0.003, y la deformación en la fibra de tracción extrema es cero. El punto de flexión puro es donde la capacidad de carga axial es cero.. Entre la transición del punto de descompresión al punto de flexión puro, se logra una condición equilibrada. En este punto, la deformación del hormigón está en su límite (mi_c= 0,003), y la deformación del acero exterior alcanza el rendimiento (mi_s= 0,0025). Cualquier combinación de carga axial y momento flector fuera del diagrama causará fallas..

Resistencia a la compresión axial nominal máxima para el diseño (Op_norte)

La resistencia axial de diseño de una sección solo se limitará a 80-85% de la resistencia axial nominal para tener en cuenta la excentricidad accidental.

\( {Op}_ _{norte} = ø × {PAG}_ _{los} \) (8a)

\( {PAG}_ _{los} = F × [0.85 × {F}_ _{c} × ({A}_ _{gramo} – {A}_ _{S t}) + ({F}_ _{y} × {A}_ _{S t}) ] \) (8b)

F = 0.80 (Corbatas)

F = 0.85 (Espiral)

A_GRAMO = Área bruta de la sección transversal del pilote

A_{S t} = Área total de las barras de acero longitudinales

F_y = Límite elástico de las barras de acero

Resistencia nominal a la flexión (dolorido_norte)

La construcción del diagrama de interacción para la columna implica graficar una serie de valores de P_norte y M_norte. Valores para P_norte será equivalente a la suma de las fuerzas de tracción y compresión, como se muestra en las Figuras 2a y 2b, mientras que la correspondiente M_norte se calcula resolviendo estas fuerzas sobre el eje neutral. Estas fuerzas incluyen la fuerza de compresión que actúa sobre el área de compresión y las fuerzas ejercidas por cada una de las barras de refuerzo, que pueden ser de compresión o tracción.. A continuación se sugiere un procedimiento general para construir un diagrama de interacción utilizando las ecuaciones presentadas.

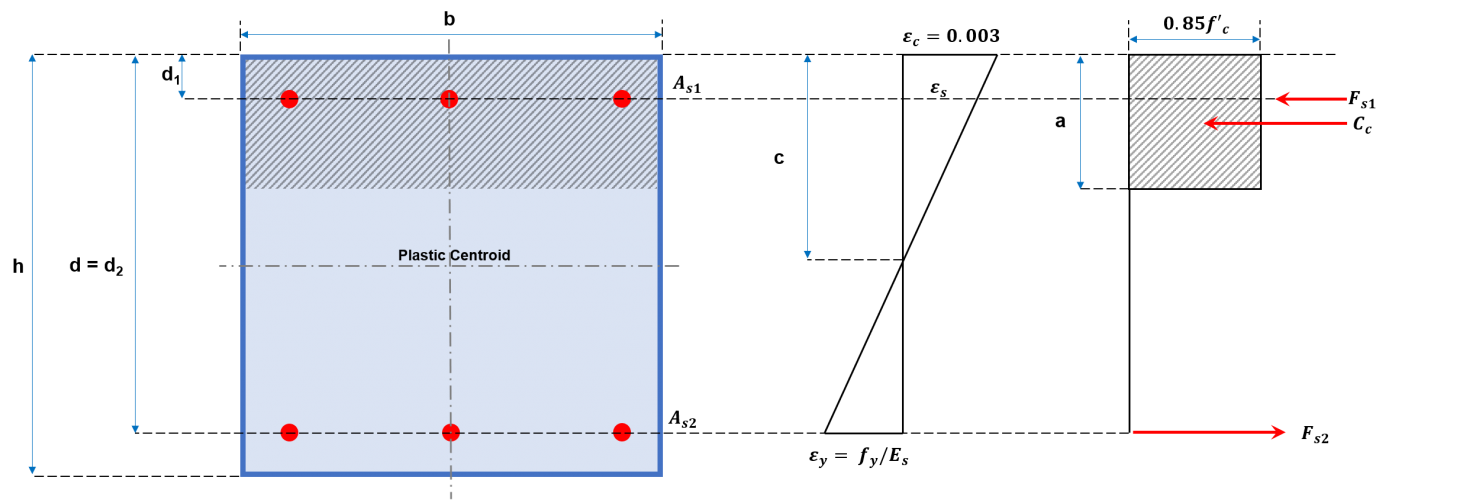
Figura 2a: Sección transversal de columna rectangular

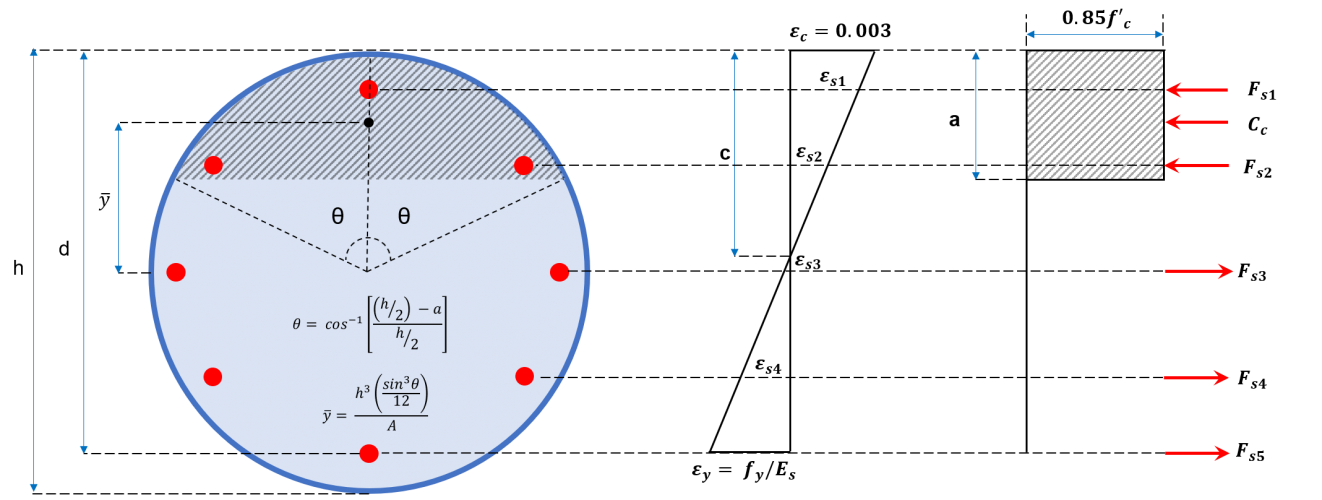
Figura 2b: Sección transversal de columna circular

Procedimiento general para diagrama de interacción de una columna

(1) Calcule el valor de P_los y P_norte (ecuaciones 8a y 8b).

(2) Determinar cy las deformaciones en los refuerzos..

\( c = 0.003 × frac{{d}_ _{1}}{0.003 + (Z + {mi}_ _{y})} \) (9)

c = profundidad del eje neutro

mi_y = Deformación del acero = f_y/E_s

Z = valor arbitrario (0, -0.5, -1.0, -2.5)

Se considerará una serie de casos seleccionando varias ubicaciones del eje neutral, c. Para establecer las ubicaciones del eje neutro, Se seleccionarán diferentes deformaciones del acero multiplicando un valor arbitrario Z por el límite elástico del acero.. Existe una amplia gama de valores para Z. sin embargo, solo hay cuatro puntos obligatorios para usar en el diagrama de interacción.

• Z = 0: en este punto, la deformación en la capa extrema en tensión es cero. Este punto marca el cambio de un empalme traslapado de compresión permitido en todas las barras longitudinales a un empalme traslapado de tensión.
• Z = -0.5: esta distribución de deformaciones afecta la longitud del empalme traslapado de tensión en una columna & se representa habitualmente en un diagrama de interacción.
• Z = -1: esto marca el punto de una condición equilibrada. Esta distribución de deformaciones marca el cambio de fallas por compresión originadas por aplastamiento de la superficie de compresión de la sección a fallas por tracción iniciadas por la fluencia de la armadura longitudinal..
• Z = -2.5: este punto corresponde al límite de deformación controlada por tensión de 0.005.

(3) Calcule las tensiones en las capas de refuerzo.

\({F}_ _{y} ={mi}_ _{y} × {E}_ _{s} \) (10)

F_y = Tensión en acero

mi_y = Deformación en acero

\({mi}_ _{y} = frac{c -{d}_ _{i}}{c} × 0.003 \) (11)

E_s = Módulo de elasticidad del acero

(4) Determine la altura del bloque de tensión de compresión, a.

\(a = {si}_ _{1} × c \) (a ≤ h)(12)

Para f’c ≤ 4000 psi (28 MPa):

si₁ = 0.85

Para f'c > 4000 psi (28 MPa):

\( {si}_ _{1} = 0.85 – \frac{0.05 × (f'c – 4000)}{1000} \) (Imperial)

\( {si}_ _{1} = 0.85 – \frac{0.05 ×(f'c – 28)}{7} \) (Métrico)

(5) Calcule las fuerzas en el hormigón y el acero..

Área del bloque de tensión compresiva:

\({A}_ _{c} = a × b \) (Sección transversal rectangular)

\({A}_ _{c} ={h}^{2} × frac{θ – pecadoθ cosθ}{4} \) (Sección circular)

Fuerza compresiva en hormigón:

\({C}_ _{c} = (0.85 × f'c) × {A}_ _{c}\) (14)

Fuerza de tracción en acero (d_i≤ a):

\({F}_ _{y} = {F}_ _{y} × {A}_ _{y} \) (15)

Fuerza compresiva en acero (d_i > a):

\({F}_ _{y} = [{F}_ _{y} – (0.85 × f'c)] × {A}_ _{y} \) (16)

(6) Calcule la capacidad axial (PAG_norte).

\({PAG}_ _{norte} = {C}_ _{c} + Σ {F}_ _{y} \) (17)

(7) Calcule la capacidad de flexión (M_norte).

\({M}_ _{norte} = [{C}_ _{c} × (\frac{h}{2} – \frac{a}{2})]+ Σ [{F}_ _{y} × (\frac{h}{2} – {d}_ _{i}) \) (18)

(8) Calcule el valor del factor de reducción de resistencia (ø).

Como se muestra en la tabla 1, el factor de reducción de resistencia tanto para axial como para flexión varía de 0.60 a 0.90. Sección de 21.2 de ACI 318-14 demuestra su valor por el momento, fuerza axial, o momento combinado y fuerza axial, como se muestra en la Tabla 2 a continuación.

Clasificación	Espiral	Atado
Compresión controlada	0.75	0.65
Transición de compresión a tensión	0.75 + [50 × (mit – 0.003) ]	0.65 + [(250/3) × (mit – 0.003) ]
Tensión controlada	0.90	0.90

Tabla 2: Factores de reducción de fuerza para axiales, momento o combinar axial y momento (Tabla 21.2.2, ACI 318-14)

(9) Repita los pasos 2-8 con varios valores para Z.

(10) Trace en el diagrama los valores de øP_norte y øM_norte.

Diseño de pilotes de hormigón con SkyCiv Free Foundation Calculator

Calculadora de base gratuita SkyCiv lo ayuda con el diseño de pilotes de hormigón y otras tareas, como el diseño de cimientos y pilotes de hormigón. Compruébelo ahora para explorar cómo nuestra calculadora puede ayudarlo con su proyecto de pilotes de concreto!

Calculadora de diseño de cimientos

Referencias

• • Requisitos del Código de Construcción para Hormigón Estructural (2014). C.A.! 318-14 Instituto Americano del Concreto.
  • Hsiao, J.K. (2012). Efectos del eje de flexión en el momento de carga (PM) Diagramas de interacción para columnas de hormigón circulares que utilizan un número limitado de barras de refuerzo longitudinales. Revista Electrónica de Ingeniería Estructural 12 (1). Obtenido de http://www.ejse.org