Ejemplo de diseño de placa base AISC Código estadounidense

A continuación se muestra un ejemplo de algunos cálculos de placas base estadounidenses que se usan comúnmente en el diseño de placas base.. A menudo, al diseñar placas base, consideraremos algunos controles diferentes relacionados con los diversos componentes de una placa base, a saber:

• La base de hormigón – generalmente verificado contra las fuerzas de compresión y de apoyo en referencia a ACI 318
• las soldaduras – hay que revisar las soldaduras, para garantizar que brinden la sujeción adecuada y no fallen bajo estrés al AISC 360
• Pernos de anclaje – puede fallar debido a una serie de razones, como se muestra a continuación en los cálculos de diseño de pernos de anclaje de ejemplo para AISC
• miembro de acero (Columna) cheques – generalmente basado en estándares locales de diseño de acero

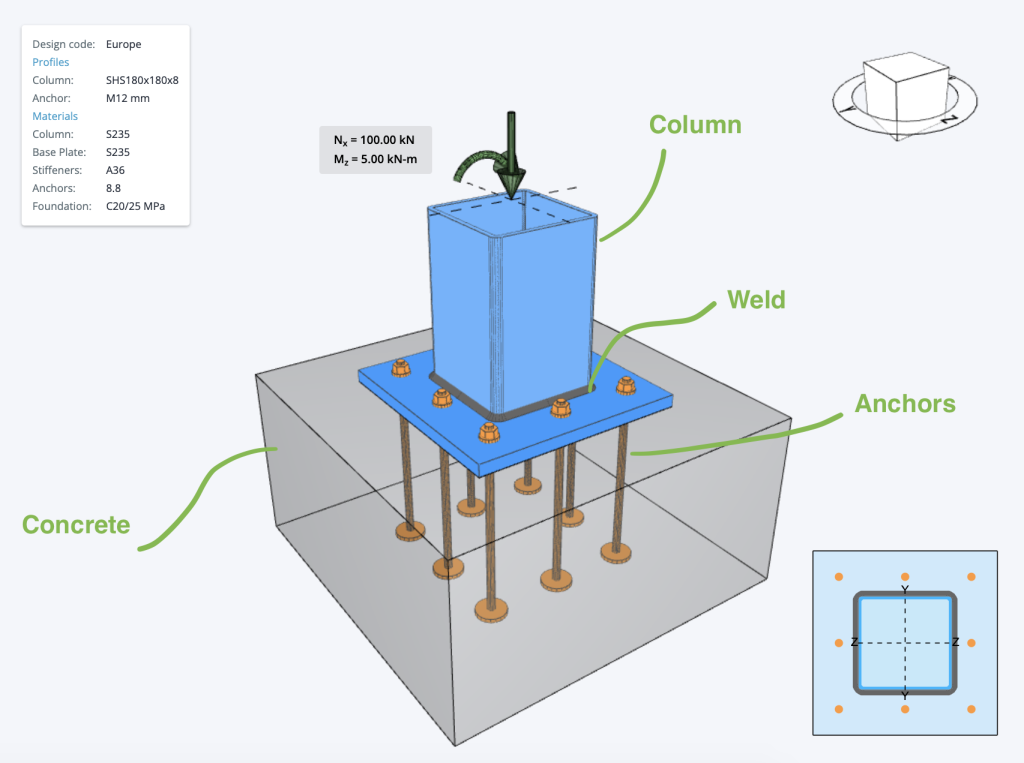
Actualmente, la Diseño de placa base de acero módulo implementa las siguientes comprobaciones a continuación. La versión de pago de este software., incluye cálculos detallados paso a paso, para que los ingenieros puedan revisar exactamente cómo se hacen estos cálculos!

Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:

Calculadora de Placas Base

 

---

Combinaciones de carga:

El Diseño de placa base de acero el uso de combinaciones de carga factorizadas bajo ASCE 7-10/16 se aplica de la siguiente manera:

1. \(1.4D)
2. \(1.2re + 1.6L + 0.5(L_{r} \texto{ o } S texto{ o } R)\)
3. \(1.2re + 1.6(Lr text{ o } S texto{ o } R) + (L texto{ o } 0.5W)\)
4. \(1.2re + 1.0W + L + 0.5(Lr text{ o } S texto{ o } R)\)
5. \(1.2re + 1.0E + L + 0.2S)
6. \(0.9re + 1.0W )
7. \(0.9re + 1.0MI)

dónde :

\(D) = carga muerta
\(L ) = carga viva
\(L_{r}\) = carga viva del techo
\(S) = Carga de nieve
\(R ) = Carga de lluvia
\(MI) = Terremoto
\(W ) = Carga de viento

Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:

Calculadora de Placas Base

 

---

Comprobación de rodamientos de hormigón ACI:

El Diseño de placa base de acero comprueba la resistencia portante del hormigón (compresión) diseño según AISC 360-16 Eq. J8-2.

\( F_{b} = phi _{Llevando} \veces 0.85 \veces f'_{c} \veces A_{1} \veces sqrt{ \frac{ UNA_{2} }{ UNA_{1} } } \leq F_{b, límite} = 1.70 \veces f'_{c} \veces A_{1} \)

dónde:
\( F'_{c} \) – resistencia a la compresión del hormigón
\( UNA_{1} \) - área de la placa base en contacto con la superficie del hormigón
\( UNA_{2} \) - superficie de apoyo de hormigón
\( \fi_{Llevando} \) – factor de resistencia para el hormigón ( valor predeterminado = 0.65 )

Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:

Calculadora de Placas Base

 

---

Comprobación del diseño de soldadura AISC:

El Diseño de placa base de acero comprueba la conformidad del diseño de soldadura con AISC 360-16 J2

\( (i) R_{norte} = R_{nulo} + R_{nwt} \)

o

\( (ii) R_{norte} = 0.85R_{nulo} + 1.5R_{nwt} \)

dónde:

\(R_{nulo} \) = resistencia nominal total de las soldaduras de filete cargadas longitudinalmente.
\(R_{nwt} \) = resistencia nominal total de las soldaduras de filete cargadas transversalmente.

Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:

Calculadora de Placas Base

---

Comprobación de diseño de anclaje ACI:

El Diseño de placa base de acero comprueba los parámetros de anclaje se aplica utilizando las disposiciones del código de ACI 318-19 bajo el capítulo 17.

Las varillas de anclaje están diseñadas según AISC 360-16 - J9 y ACI 318-19 - Capítulo 17. Se evalúan las siguientes resistencias de los pernos de anclaje:

• Resistencia del acero del ancla en tensión y cortante, \( \phi N_{a} \) y \( \no V_{a} \).
• Resistencia al desprendimiento del hormigón en tensión y cizallamiento, \( \phi N_{cbg} \) y \( \no V_{cbg} \).
• Resistencia a la extracción del hormigón, \( \phi N_{pag} \).
• Resistencia al reventón de la cara lateral del hormigón, \( \phi N_{sb} \).
• Fuerza de extracción del hormigón del anclaje a cortante, \( \no V_{cp} \).

Resistencia del acero del ancla en tensión y cortante

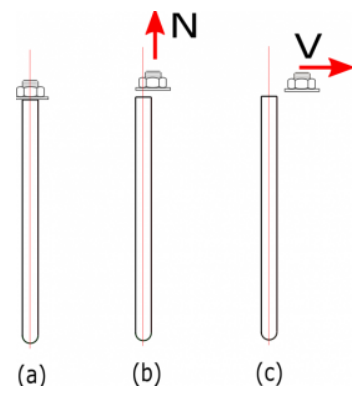
Figura A. (a) perno irrompible (b) rotura de pernos por falla de tensión (c) separación del perno debido a falla por cortante

La resistencia del acero factorizado del ancla en tensión y cortante se determina de acuerdo con ACI. 318-19 - 17.6.1.2 y 17.7.1 como

Para la tensión

\( \phi _{tensión, Congreso Nacional Africano} NORTE_{a} = phi _{tensión, Congreso Nacional Africano} UNA_{se,norte}F_{uta} \flecha correcta \) ecuación 17.6.1.2

Para cizalla

\( \phi _{el cortante, Congreso Nacional Africano} V_{a} = phi _{el cortante, Congreso Nacional Africano} 0.6UNA_{se,V }F_{uta} \flecha correcta \) ecuación 17.7.1.2b

dónde:

• \( \phi _{tensión, Congreso Nacional Africano} \) - factor de reducción de resistencia para anclajes en tensión ( valor predeterminado = 0.75 )
• \( \phi _{el cortante, Congreso Nacional Africano}\) - factor de reducción de resistencia para anclajes a cortante ( valor predeterminado = 0.65 )
• \( UNA_{se,norte}\) - es el área de la sección transversal efectiva de un ancla en tensión.
• \( UNA_{se,V }\) - es el área de la sección transversal efectiva de un ancla en cortante.
• \( F_{uta}\) – la resistencia a la tracción especificada del acero del anclaje y no debe ser mayor que \(1.9F_{sí}\) y 125 KSI (861.845 Mpa)

Resistencia a la rotura del hormigón

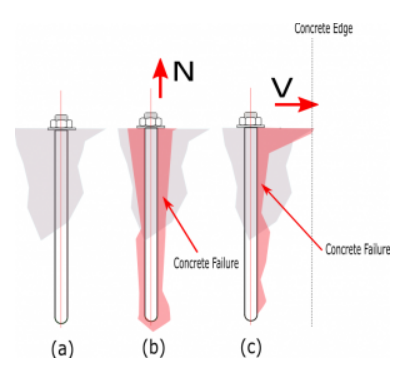
Figura B. (a) Resto de pernos en concreto (b) ruptura del concreto debido a la fuerza de tensión (c) ruptura del concreto debido a la fuerza de corte

 

La resistencia al desprendimiento del hormigón factorizado del anclaje en tracción y cortante se determina de acuerdo con ACI. 318-19 - 17.6.2 y 17.7.1 como

\( \phi N_{cbg} = phi frac{ UNA_{Carolina del Norte} }{ UNA_{Recuerda} } \psi_{CE,norte} \psi_{ed,norte} \psi_{c,norte} \psi_{cp,norte} NORTE_{b} \flecha correcta \) ecuación 17.6.2.ab

dónde:

\( \fi \) – factor de reducción de resistencia para anclajes en tensión ( valor predeterminado = 0.75 ).
\( UNA_{Carolina del Norte} \) – Falla proyectada de hormigón de anclajes individuales o grupales..
\( UNA_{Recuerda} \)- Proyecto de área de falla de concreto de un solo anclaje, para el cálculo de la resistencia en tensión si no está limitado por la distancia al borde o el espaciado.

\( \psi_{CE,norte} \) - Factor de excentricidad de ruptura en tensión.

\( \psi _{CE,norte} = frac{1.00}{ 1 + \frac{e ^{"}_ _{norte}}{1.5 h_{ef}} } \leq 1.00 \flecha correcta \) ecuación 17.6.2.3.1

\( \psi_{ed,norte} \) - Factor de efecto de ruptura en tensión..

(a) \( \texto{Si } C_{a,min} \geq 1.5h_{ef} \texto{ luego } \psi _{ed,norte} = 1.00 \) ecuación 17.6.2.4.1a

y

(b) \( \texto{Si } C_{a,min} < 1.5h_{ef} \texto{ luego } \psi _{ed,norte} = 0.70 + 0.3\frac{C_{a,min}}{1.5h_{ef}} \) ecuación 17.6.2.4.1b

\( \psi_{c,norte} \) - Factor de ruptura de grietas en tensión.

\( \psi _{c,norte} = 1.25 \) para anclajes empotrados

\( \psi_{cp,norte} \) - Factor de ruptura en tensión.

(a) \( \texto{Si } C_{a,min} \geq C_{C.A} \texto{ luego } \psi _{cp,norte} = 1.00 \) ecuación 17.6.2.4.1a

y

(b) \( \texto{Si } C_{a,min} < C_{C.A} \texto{ luego } \psi _{cp,norte} = frac{ C_{a,min} }{ C_{C.A}} \geq frac{ 1.5h_{ef} }{ C_{C.A} } \) ecuación 17.6.2.4.1b

\( NORTE_{b} \) – resistencia básica al desprendimiento del hormigón en tensión de un solo anclaje en hormigón fisurado.

Resistencia a la extracción del hormigón

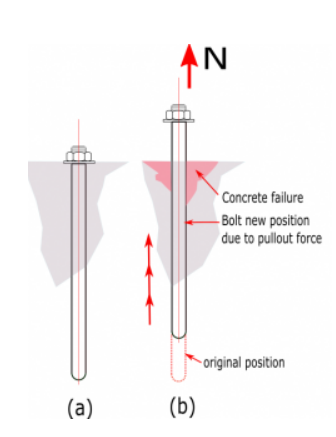
Figura C. (a) Resto de pernos en concreto (b) desprendimiento del perno del concreto debido a la fuerza de tensión

 

La resistencia a la extracción del hormigón factorizado de un anclaje se define en ACI. 318-19 - 17.6.3 como

ϕN_pn = ϕΨ_c,PAG norte_pag

dónde:

\( \fi \) – factor de reducción de resistencia para anclajes en tensión ( valor predeterminado = 0.70 ).
\( \psi _{c, PAG} \) – factor de modificación para la condición del hormigón

Para hormigón fisurado:

\( \psi _{c, PAG} \) = 1.0

Para hormigón no fisurado:

\( \psi _{c, PAG} \) = 1.4

\( NORTE_{pag} \) – Fuerza de extracción del ancla

Para hormigón fisurado:

\( NORTE_{pag} = 8A_{brg}f ^{"}_ _{c}\) ecuación 17.6.3.2.2a

Para hormigón no fisurado:

\( NORTE_{pag} = 0.9f ^{"}_ _{c}mi_{h}D_{a} \flecha correcta \) ecuación 17.6.2.2.b

dónde \( 3D_{a} \leq e_{h} \leq 4.5d_{a} \)

\( f ^{"}_ _{c} \) – resistencia a la compresión especificada del hormigón.
\( UNA_{brg} \) – área de apoyo neta de la cabeza del montante, perno de anclaje o barra deformada con cabeza.
\( mi_{h} \) – distancia desde la superficie interior del eje de un perno en J o un perno en L a la punta exterior de la J- o perno en L.
\( D_{a} \) – diámetro exterior del ancla o diámetro del eje del perno con cabeza, perno con cabeza, o perno en forma de gancho.

Resistencia al reventón de la cara lateral del hormigón

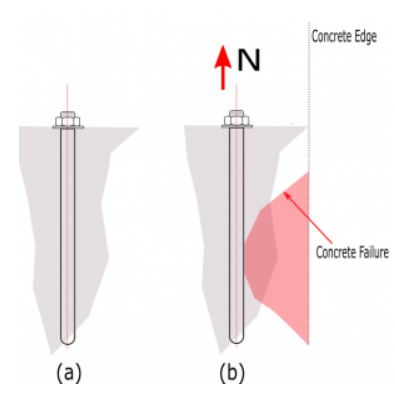
Figura D. (a) Resto de pernos en concreto (b) perno con falla de concreto (Golpe lateral) cerca del borde a la fuerza de tensión

 

La resistencia al reventón de la cara lateral de hormigón factorizado de un anclaje se define en ACI 318-19 - 17.6.4 como

\( \phi N_{sb} = 160C_{a1}\sqrt{UNA_{brg}}\lambda _{a} \sqrt{f ^{"}_ _{c} } \flecha correcta \) ecuación 17.6.4.1

dónde:

\( f ^{"}_ _{c} \) – resistencia a la compresión especificada del hormigón.
\( UNA_{brg} \) – área de apoyo neta de la cabeza del montante, perno de anclaje o barra deformada con cabeza.
\( \lambda_{a} \) – factor de modificación para reflejar las propiedades mecánicas reducidas del hormigón ligero en determinadas aplicaciones de anclaje de hormigón.

Resistencia al desprendimiento de hormigón del anclaje

\( \texto{V }_ _{ \texto{cp} } = text{k}_ _{cp} \tiempos texto{norte}_ _{cp} \) 

o 

\( \texto{V }_ _{ \texto{cpg} } = text{k}_ _{cpg} \tiempos texto{norte}_ _{cpg} \)El reventón por apalancamiento del concreto se evalúa en las ecuaciones anteriores y los cálculos se basan en la resistencia entre la varilla de anclaje y el concreto donde suele fallar la instalación del anclaje posterior a la instalación., ver la Figura E a continuación.

Figuras E. (a) Resto de pernos en concreto (b) perno con falla de concreto (hacer palanca) debido a la fuerza de corte. 

 

Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:

Calculadora de Placas Base