İçindekiler
- genel bakış – Atalet Momenti Nedir?
- Misal – Atalet Momenti Nasıl Hesaplanır?
- Formül ve Denklemler
- Hesap makineleri
- Alıştırma Soruları
genel bakış – Atalet Momenti Nedir??
Yapı mühendisliği bağlamında, Atalet Momenti, bir yapısal elemanın bükülme ve burulma kuvvetlerine direnme yeteneğini belirlemek için kullanılan bir kesit özelliğidir.. Bu genellikle bölümlerin sertliğinin ve yük altındaki mukavemetinin oldukça iyi bir göstergesidir. Daha yüksek atalet momenti, yapının bükülme ve sapmaya karşı daha iyi donatıldığı anlamına gelir, kirişlerin tasarımında bunu önemli bir faktör haline getiriyor, sütunlar, ve diğer yük taşıyan bileşenler. Yan not olarak: Bazen bu yanlış bir şekilde ikinci an olarak tanımlanır. eylemsizlik, ancak bu yanlış. Atalet Momentinin diğer isimleri:: alan eylemsizlik momenti, veya ikinci anı alan.
Misal – Kiriş Kesitinin Atalet Momenti Nasıl Hesaplanır
Bir kiriş bölümünün atalet momentini bulmadan önce (bir kiriş bölümünün ikinci alan momenti olarak da bilinir), ağırlık merkezi (veya kütle merkezi) bilinmeli. Örneğin, yatay ile ilgili bölümün eylemsizlik momenti (XX) eksen gerekliydi sonra dikey (Y) önce centroid gerekli olacaktır (Lütfen öğreticilerimizi görüntüleyin bir kiriş bölümünün ağırlık merkezinin hesaplanması ve statik/ilk alan momentinin hesaplanması).
Başlamadan önce, eğer arıyor olsaydın Serbest Atalet Momenti Hesaplayıcı daha fazla bilgi edinmek için lütfen bağlantıya tıklayın. Bu ağırlık merkezini hesaplayacak, eylemsizlik momenti, ve diğer sonuçlar ve hatta size adım adım hesaplamaları gösterir! Ama şimdilik, adım adım bir kılavuza ve eylemsizlik momentinin nasıl hesaplanacağına dair bir örneğe bakalım:
Adım 1: Kiriş bölümünü parçalara ayırın
Alan atalet momentini hesaplarken, daha küçük segmentlerin eylemsizlik momentini hesaplamalıyız. Bunları basit dikdörtgen bölümlere ayırmaya çalışın. Örneğin, aşağıdaki I-kiriş bölümünü düşünün, bu da centroid öğreticimizde yer aldı. Bu bölümü ikiye ayırmayı seçtik 3 dikdörtgen segmentler:
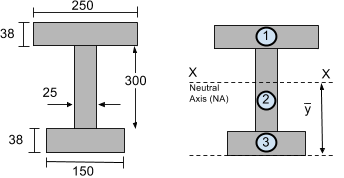
Adım 2: Nötr Ekseni Hesaplayın (NA)
Nötr Eksen (NA) veya yatay XX ekseni ağırlık merkezinde veya kütle merkezinde bulunur. Centroid öğreticimizde, bu bölümün ağırlık merkezi daha önce bulundu 216.29 bölümün altından mm – bu bizim kapsamımızda bir şeklin ağırlık merkezi nasıl bulunur Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür. Bunlar ayrıca basitçe bizim merkez hesap makinesi ya da sıradan merkez denklemleri.
Merkezi hesaplama, veya Nötr Eksen, içinde önemlidir kirişin eylemsizlik momenti nasıl hesaplanır, atalet momentinin hareket ettiği eksen bu olduğundan.
Adım 3: Atalet Momentini Hesaplayın
Bölümün toplam eylemsizlik momentini hesaplamak için kullanmamız gereken “Paralel Eksen Teoremi”:

Üç dikdörtgen parçaya böldüğümüz için, bu bölümlerin her birinin eylemsizlik momentini hesaplamalıyız. Bir dikdörtgenin merkez ekseni etrafındaki eylemsizlik momenti denkleminin basitçe:
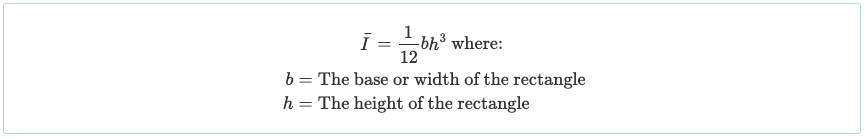
Diğer şekillerin eylemsizlik momenti genellikle ders kitaplarının önünde / arkasında veya bu kılavuzda belirtilir. eylemsizlik momenti şekilleri. Bununla birlikte, dikdörtgen şekli kiriş bölümleri için çok yaygındır, bu yüzden muhtemelen ezberlemeye değer.
Şimdi kullanmak için ihtiyacımız olan tüm bilgilere sahibiz “Paralel Eksen Teoremi” ve I-kiriş bölümünün toplam eylemsizlik momentini bulun. Eylemsizlik anımız örneğimizde:

Böylece, kiriş kesitleri için moment alanını hesaplama kılavuzumuz var.. Bu sonuç yapısal mühendislikte kritiktir ve bir kirişin sapmasında önemli bir faktördür.. Eğiticiden keyif aldığınızı umarız ve sahip olduğunuz tüm yorumları dört gözle bekleriz. Daha fazla bilgi için, hakkındaki eğitimimizi ziyaret edin Eylemsizlik Momenti Formülü ve Denklemleri.
Formül ve Denklemler
Her bölüm türü (dikdörtgen, Işınlıyorum, Sirküler) hızlı hesaplama için kendi formülü vardır. Bunlar, mühendislerin bu önemli özelliği hızlı ve kolay bir şekilde hesaplamasına olanak tanıyan basitleştirilmiş denklemlerdir..
Denklemler yukarıdaki adımların basitleştirilmiş bir ifadesidir. Örneğin, İçi Boş bir Dikdörtgenin eylemsizlik momenti formülü temel olarak daha büyük bölümün MOI'sidir – daha küçük (iç) Bölüm:

[matematik] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [matematik]
SkyCiv ortak kullanım için kullanışlı bir kaynak oluşturdu Atalet Momenti formülü.
Hesap makineleri
Atalet momentinin nasıl hesaplanacağı konusunda birçok yol vardır., Bunlardan biri, süreci kolaylaştırmak için yazılım kullanmaktır..
SkyCiv Bölüm Oluşturucu Atalet momenti hesaplayıcısının çok ötesine geçen tam donanımlı bir kesit tasarım aracıdır. Ayrıca eylemsizlik momentinin nasıl bulunacağına ilişkin adım adım hesaplamaları da gösterecektir.:
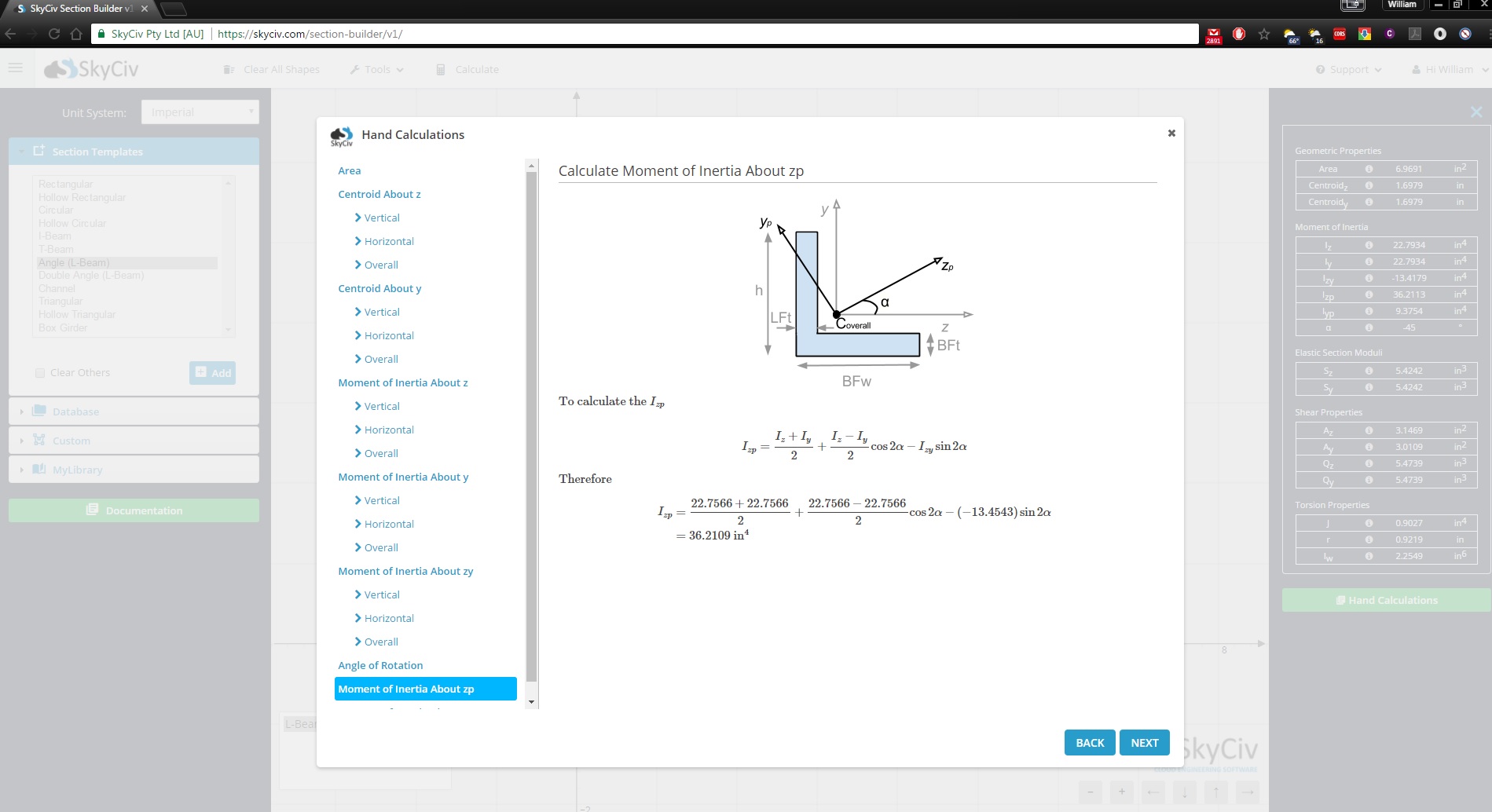
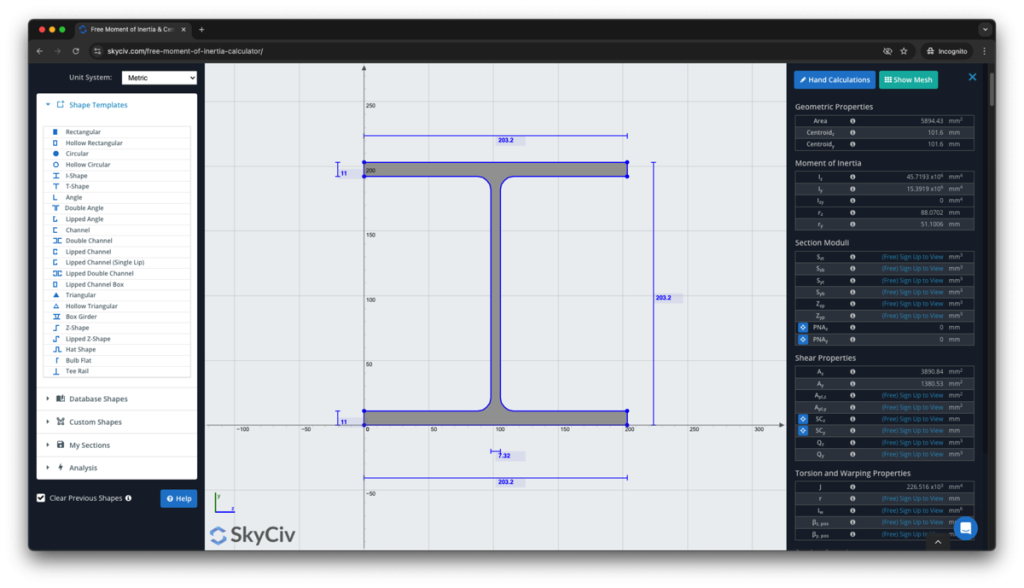
SkyCiv yazılımı hakkında daha fazlasını keşfetmek için bugün kaydolun, ya da rezervasyon yap ÜCRETSİZ DEMO mevcut kullanıcılar için mühendislik projelerinizde yardım almak için!
bunlara ek olarak, SkyCiv'de ücretsiz Bölüm Özelliği Hesaplayıcı Hızlı Tasarım kütüphanesinin bir parçası olarak. Basitleştirilmiş bir araçtır, fakat aynı zamanda ortak kesit şekillerinin eylemsizlik momentini de hesaplayacaktır..
Alıştırma Soruları
Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür 1: Dikdörtgen Bölüm
Sorun: Atalet momentini hesaplayın (Ixx ve Iyy) genişliğe sahip dikdörtgen bir bölüm için (b) nın-nin 200 mm ve yükseklik (h) nın-nin 300 mm.
Çözüm: Dikdörtgenin eylemsizlik momenti formülleri:
Verilen değerlerin yerine koyma:
- b=200 mm
- h=300 mm
Ixx için:
Iyy için:
Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür 2: I-Işın
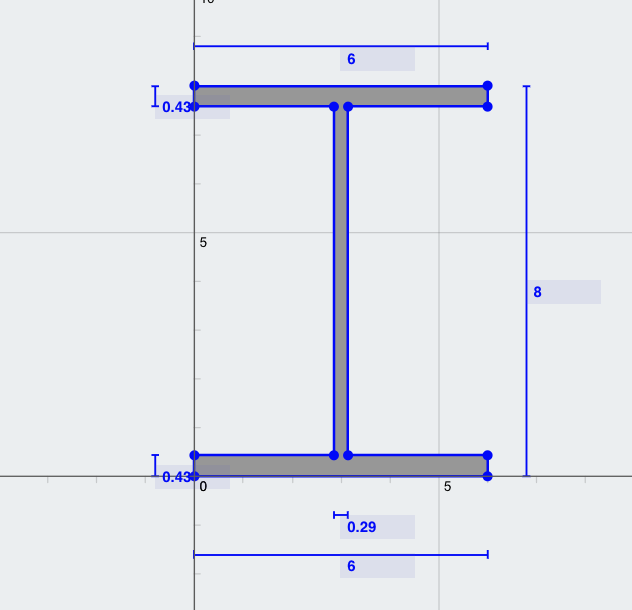
Sorun: Ana eksenin eylemsizlik momentini hesaplayın (Ixx) aşağıdaki boyutlara sahip bir I-kiriş bölümünün:
- Üst flanş genişliği (TFw) = 6 içinde
- Üst flanş kalınlığı (TFt) = 0.43 içinde
- Bölüm Derinliği = 6 içinde
- Web kalınlığı (Wt) = 0.29 içinde
- Alt flanş genişliği (BFw) = 6 içinde
- Alt flanş kalınlığı (BFt) = 0.43 içinde
Çözüm:


