Bu makalede, ACI-318-19'un son sürümünü kullanarak bir Döşeme Tasarım Örneği geliştireceğiz: “Yapısal Beton için Bina Kodu Gereklilikleri,” ACI tarafından kabul edilen bir yöntemle yazılım sonuçlarının ve elle yapılan hesaplamaların karşılaştırılmasına odaklanan Betonarme Alçak Binanın SkyCiv'de modellenmesinden oluşur: “Döşemeler için Doğrudan Tasarım Yöntemi.” Bu prosedür, donatı miktarını ve döşemedeki konumunu belirlemek için binanın ana yönleri ve çerçeveleri boyunca farklı şeritlere toplam momentin uygun faktörlerle atanmasını içerir..
Umarız önceki makaleyi okumuşsunuzdur, S3D'de Plaka Tasarımı, kendinizi SkyCiv kullanarak kalıp modelleme ve tasarlama konusunda tanıtmak. Dikkate almanızı önerdiğimiz başka bir yararlı bilgi de şu adreste bulunmaktadır: plaka modeli nasıl yapılır? Her iki belgeyi de okumayı tamamladığınızda, Aşağıdaki tam işlenmiş levha karşılaştırma örneğine dalmaktan çekinmeyin!
Genel Bina Düzeni
Aşağıdaki resimler, hesaplanacak örneğin izometrik görünümünü ve plan boyutlarını göstermektedir.. Bina, kolon destekleri arasında kirişsiz iki yükseltilmiş düz levhaya sahiptir..
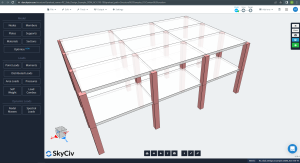
Figür 1. Bina örneğinin izometrik görünümü
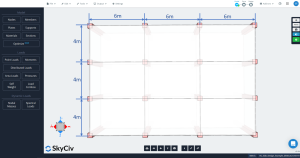
Figür 2. Döşeme planı boyutları
İki Yönlü Döşemeler için Doğrudan Tasarım Yöntemi (DDM)
Sınırlamalar
ACI 318 yerçekimi yükleri için betonarme döşemeler tasarlamak için DDM'nin kullanılmasına izin verir, geometriye göre bazı gereksinimleri toplayan, yük ilişkileri, simetri, vb. Bu sınırlamaları aşağıdaki listede özetleyebiliriz. (PCA Notları):
- “Her yönde üç veya daha fazla sürekli açıklık olmalıdır.”: Figür 2 her ana yönde üç açıklığı gösterir, boyuna ve enine. Tamam mı!
- “Döşeme panelleri, daha uzun ila daha kısa açıklık oranına sahip dikdörtgen olmalıdır (desteklerin merkez hattından merkez hattına) 2'den büyük değil.”: şekle göre 2, oran eşittir \({\çatlamak{l_1}{4}= frac{6m}{4m}=1.5 < 2}\). Tamam mı!
- “Ardışık yayılma uzunlukları (desteklerin merkez hattından merkez hattına) her yönde en fazla farklılık göstermemelidir 1/3 daha uzun açıklığın”. Açıklık uzunlukları her yönde aynıdır, 6boyuna m ve enine 4 m. Tamam mı!
- “Sütunlar, 10% açıklığın (ofset yönünde) birbirini izleyen sütunların merkez çizgileri arasındaki her iki eksenden”. Bina örneğinde sütunlarda öteleme yok. Tamam mı!
- “Yükler eşit olarak dağıtılmalıdır, faktörlenmemiş veya hizmet canlı yükü ile, faktörlenmemiş veya hizmet ölü yükünün iki katından fazla olmayan (L/D ≤ 2)”. Her yerçekimi yükünün değerlerinin alınması, oran şu şekilde tanımlanır \({\çatlamak{L}{D}= frac{2}{7.8}= 0,256 < 2}\). Tamam mı!.
- “İki yönlü kiriş destekli döşemeler için, iki dik yönde kirişlerin bağıl rijitliği, kodda verilen minimum ve maksimum gereksinimleri karşılamalıdır.” Zaten memnun; döşemelerde kiriş yok. Tamam mı!
- “Negatif anların kodla yeniden dağıtılmasına izin verilmez.” Örneğin basitliği nedeniyle, levhalardaki olumsuz anları yeniden dağıtmak gerekmeyecek. Tamam mı!.
Boyuna ve enine şerit tanımı
DDM'deki döşeme, belirli bir hat ızgarasının analizi ve tasarımı için iki ana şeride bölünmelidir.: sütun ve orta şeritler. Sütun şeritlerinin genişliği, \({\çatlamak {l_1}{4}}\) ve \({\çatlamak{l_2}{4}}\), nerede \({l_1}\) çizgi ızgarası boyunca açıklığın uzunluğu ve \({l_2}\) enine uzunluk dikeydir.
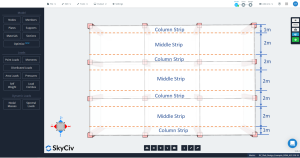
Figür 3. Boyuna kolon ve orta şeritler.
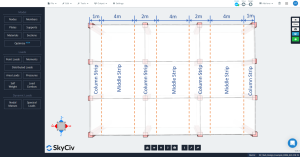
Figür 4. Enine sütun ve orta şeritler.
minimum kalınlık
ACI-318, denklemin kullanılmasını önerir: \({t_{min}}= {\çatlamak{l_n}{30}}={\çatlamak{6m-0.50m}{30}}=0,1833m = 0,20m)
Ön kesme dayanımı kontrolü
Çelik donatıyı hesaplamadan önce, levhanın kesme kapasitesinin kontrol edilmesi tavsiye edilir, biri bağlantıdaki doğrudan kesme için ve diğeri bağlantı döşeme kolonu üzerindeki zımbalama kesme kapasitesi için.
Kesme talebini hesaplamak için, aşağıdaki yerçekimi yüklerini kullanıyoruz:
- Kendinden ağırlıklı levha: \({SW={\gamma_c}\zamanlar {t_{döşeme}}={24 {\çatlamak{kN}{m^3}}}\zamanlar {0.20m}=4.8{\çatlamak{kN}{m^2}} }\)
- Üst üste bindirilmiş ölü yük: \({SD={3 {\çatlamak{kN}{m^2}}}}\)
- Toplam ölü yük (SW+SD): \({D={7.8 {\çatlamak{kN}{m^2}}}}\)
- Canlı yük (konut doluluk) : \({L={2 {\çatlamak{kN}{m^2}}}}\)
- faktörlü dayanım yükü (1.2D+1.6L): \({q_{sen}={12.56 {\çatlamak{kN}{m^2}}}}\)
İlk kesme kontrolü, “kiriş kesme” yazarak karşılık gelen bir yük grubu ekleyeceğiz, aşağıdaki görüntü, toplam kesmeyi elde etmek için dikkate alınması gereken alanı gösterir.. Her yönü inceliyoruz, daha geniş alanı alarak.
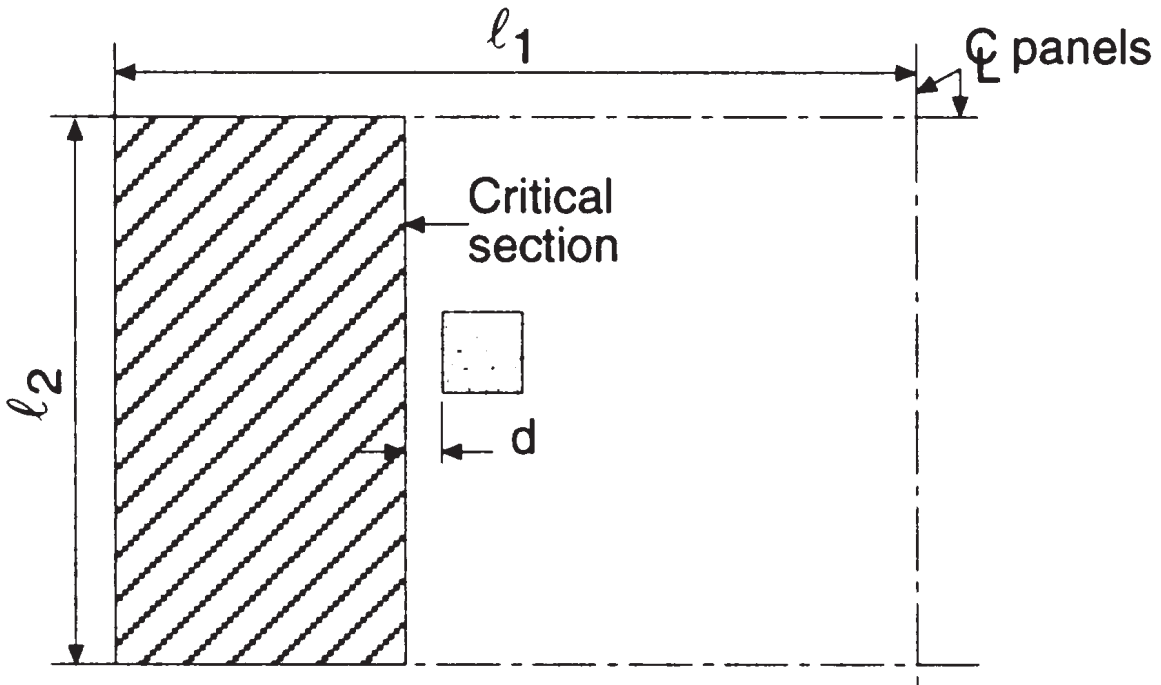
Figür 5. İç kolonda kiriş kesmesi (Nadim Hassoun ve Akthem AI-Manaseer, “Yapısal Beton Teorisi ve Tasarımı”)
Nerede:
- Boyuna yönde uzunluk açıklığı, \({l_1 = 6.0m }\)
- Enine yönde uzunluk açıklığı, \({l_2 = 4.0m}\)
- Toplam bağımlı alan, boyuna yönde kesme \({A_t = l_2 times (\çatlamak{l_1}{2}-\çatlamak{c_1}{2}-d) = 4.0m times (\çatlamak{6.0m}{2}-\çatlamak{0.50m}{2}-0.17m) = 10.32 m^2}\) (seçilmiş)
- Toplam bağımlı alan, enine yönde kesme, \({A_t = l_1 times (\çatlamak{l_2}{2}-\çatlamak{c_2}{2}-d) = 6.0m times (\çatlamak{4.0m}{2}-\çatlamak{0.50m}{2}-0.17m) = 9.48 m^2}\)
- Kare sütun boyutu, \({c_1 = c_2 = 0.50m}\)
- Mesafe d, \({d = h_{döşeme} – örtü = 0.20m – 0.03m = 0.17m }\)
Bu nedenle, iç kolondaki maksimum kiriş kesmesi
\({V_u =q_utimes A_t =12,56 {\çatlamak{kN}{m^2}}\zamanlar 10.32 m^2 = 129.62 kN }\)
Bu, kesme direncine karşı karşılaştırılacak, \({\phi_sV_c}\)
- Beton dayanımı, \({f'_c = 25 MPa}\)
- Verim inşaat demiri çelik gücü, \({f_y = 420 MPa}\)
- \({\phi_s = 0.75}\)
- \({\phi_sV_c = 0,17phi_s lambda sqrt(f'_c) b_w d; b_w=l_2}\)
\({\phi_sV_c = 0,17times 0,75times 1times sqrt(25 MPa) \zamanlar 4000 mmkez 170 mm = 433.50 kN }\)
Kesme direncinin kesme talebinden daha büyük olduğunu görebiliriz.: \({\phi_sV_c = 433.50 kN > V_u = 129.62 kN }\) Tamam mı!.
Aşağıdaki resimlere göre, iç döşeme-kolon bağlantısında delme kesme kapasitesini ve betonun karşı koyacağı kuvveti hesaplamalıyız. Kodun delme kesmesini kontrol etmedeki amacı, düşük kesme gerilimi değerlerini korumaktır..
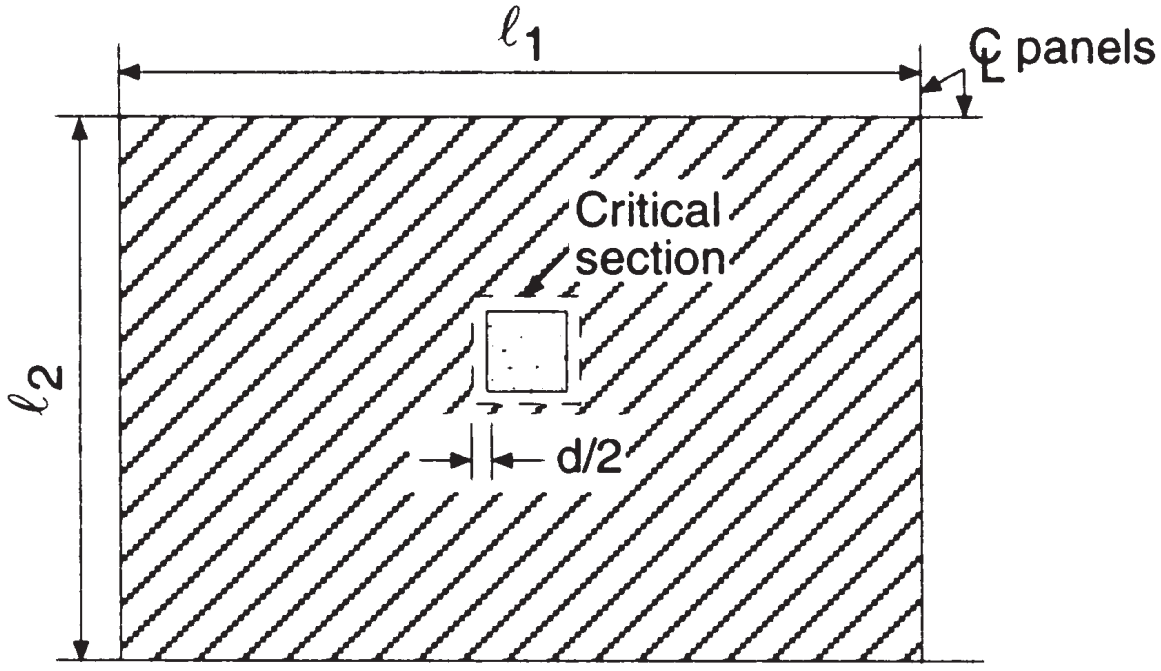
Figür 6. İç kolonda iki yönlü kesme (Nadim Hassoun ve Akthem AI-Manaseer, “Yapısal Beton Teorisi ve Tasarımı”)
- Toplam bağımlı alan, delme makası, \({A_t = l_1 times l_2 – (c_1+d)^2 = 6.0m times 4.0m – (0.50m+0.17m)montaj yüksekliğinde 23.55 m^2}\) (her iki ana yön için aynı alan)
Dayanılacak toplam kesme kuvveti
\({V_u =q_utimes A_t =12,56 {\çatlamak{kN}{m^2}}\zamanlar 23.55 m^2 = 295.79 kN }\)
İki yönlü bir döşemede zımbalama kesme kapasitesini elde etmek için, ACI-318 koduyla oluşturulan ampirik yöntemi kullanacağız, kritik bölümdeki etkin çevrede mevcut olan maksimum kayma gerilimini dikkate alan. İç sütun için daha muhafazakar ifade şu şekildedir:
- Delme kesme kapasitesi, \({\phi_sV_c = 0,33phi_s lambda sqrt(f'_c) b_0 gün; b_0=4kez (c_1+d)}\)
Bu nedenle, kesme direncine sahibiz
\({\phi_sV_c = 0,33kez 0.75 \zamanlar 1 \sqrt(25 MPa) \zamanlar (4\zamanlar (500 mm+170 mm)\kez 170mm) = 563.81 kN }\)
Kesme direncinin kesme talebinden daha büyük olduğunu görebiliriz.: \({\phi_sV_c = 563.81 kN > V_u = 295.75 kN }\) Tamam mı!.
İç kolon bağlantısında bir ve iki yönlü kesme taleplerini doğruladık. Her iki talebin de ilgili kapasitelerinden veya dirençlerinden daha az olması nedeniyle, şimdi döşeme bükme için ana donatıyı hesaplamaya geçeceğiz.
SkyCiv'de yeniyseniz, Kaydolun ve yazılımı kendiniz test edin!
Açıklık başına toplam çarpanlara ayrılmış statik moment.
Çift sabit uçlu bir kirişe dönüştürülebilen maksimum moment, şuna eşit bir izostatik momenttir: \({M=frak{wtimes {l_1}^ 2}{8}}\) (şekle bakın 6).
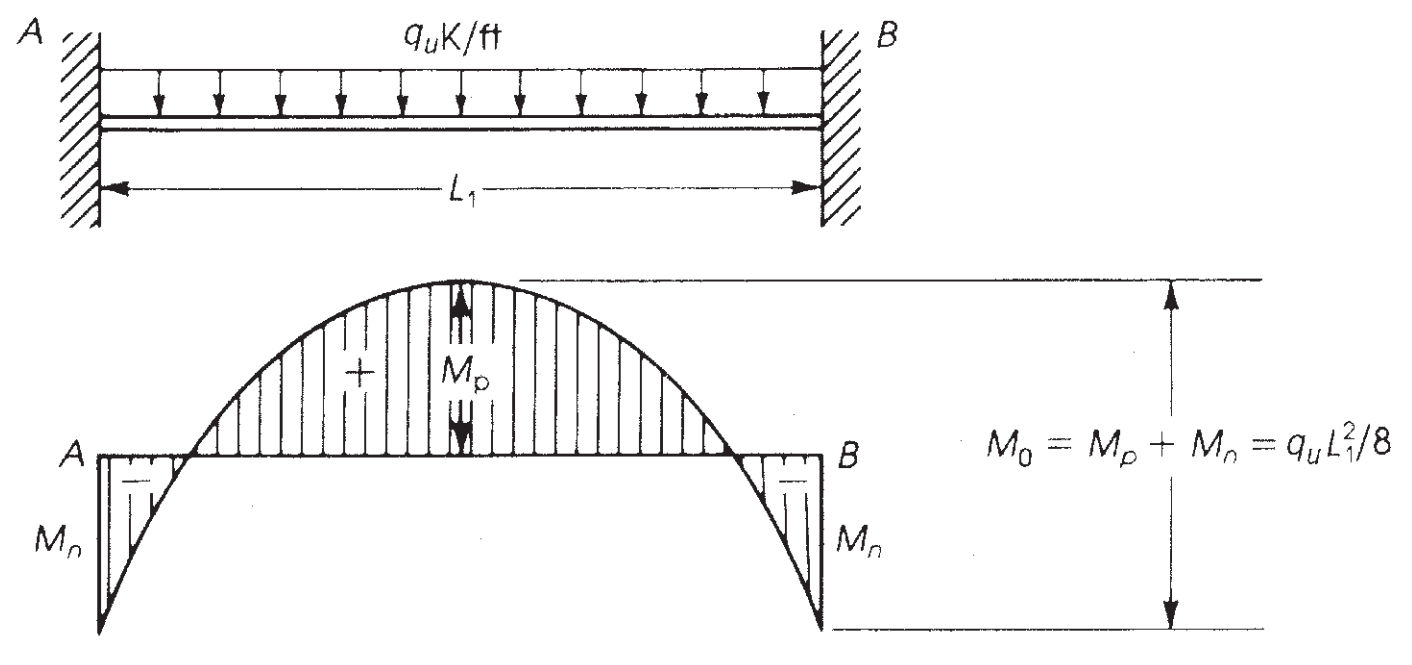
Figür 7. Sabit uçlu bir kirişte eğilme momenti. (Nadim Hassoun ve Akthem AI-Manaseer, “Yapısal Beton Teorisi ve Tasarımı”)
ACI-18 bu prensibi benimsiyor ve, Doğrudan Tasarım Yöntemi için (DDM), açıklık başına dikkate alınması gereken maksimum statik momenti belirler \({M_0}\)
boyuna yön:
- \({M_0 = frac {q_utimes l_2times {l_{n,1}}^ 2}{8}}\)
- \({M_0 = frac {12.56 {\çatlamak{kN}{m^2}}\çarpı 4.0mkez (6m-0.50m)^ 2}{8}=189,97 kN-m}\)
Enlemesine yön:
- \({M_0 = frac {q_utimes l_1times {l_{n,2}}^ 2}{8}}\)
- \({M_0 = frac {12.56 {\çatlamak{kN}{m^2}}\çarpı 6.0mkez (4m-0.50m)^ 2}{8}=115.40 kN-m}\)
Bir sonraki adım, panel tipini göz önünde bulundurarak bu toplam momenti atamaktır., iç veya dış. (şekle bakın 7). Daha sonra, açıklıkların sürekli olması nedeniyle, anı da olumlu ve olumsuz olarak bölmek gerekir. Bu son resimlerde gösterilmiştir 8 ve 9.
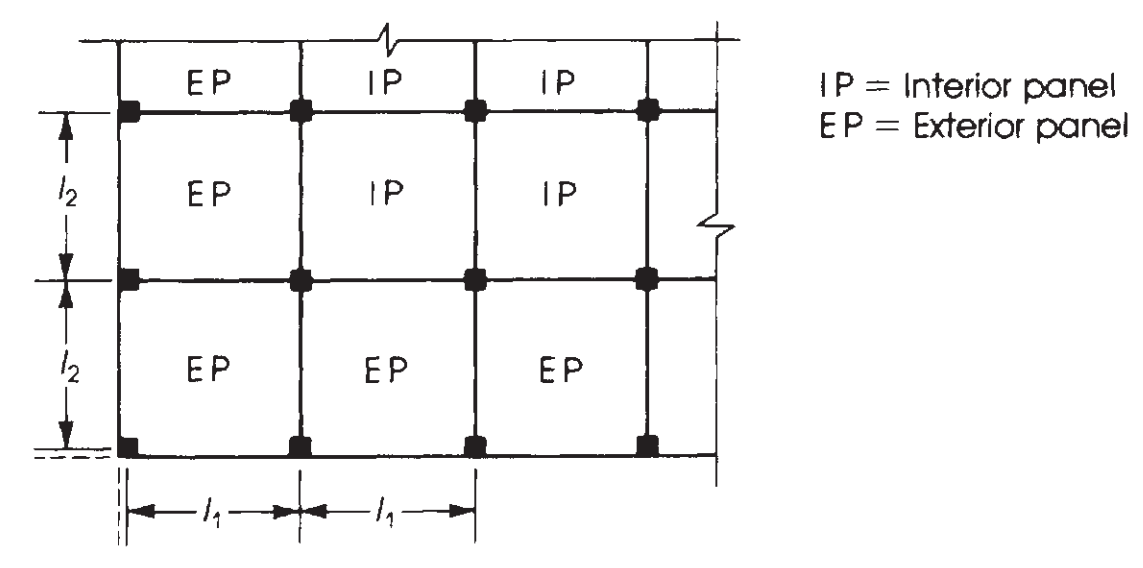
Figür 8. Döşeme planındaki göreli konumlarına göre panellerin tanımı. (Nadim Hassoun ve Akthem AI-Manaseer, “Yapısal Beton Teorisi ve Tasarımı”)
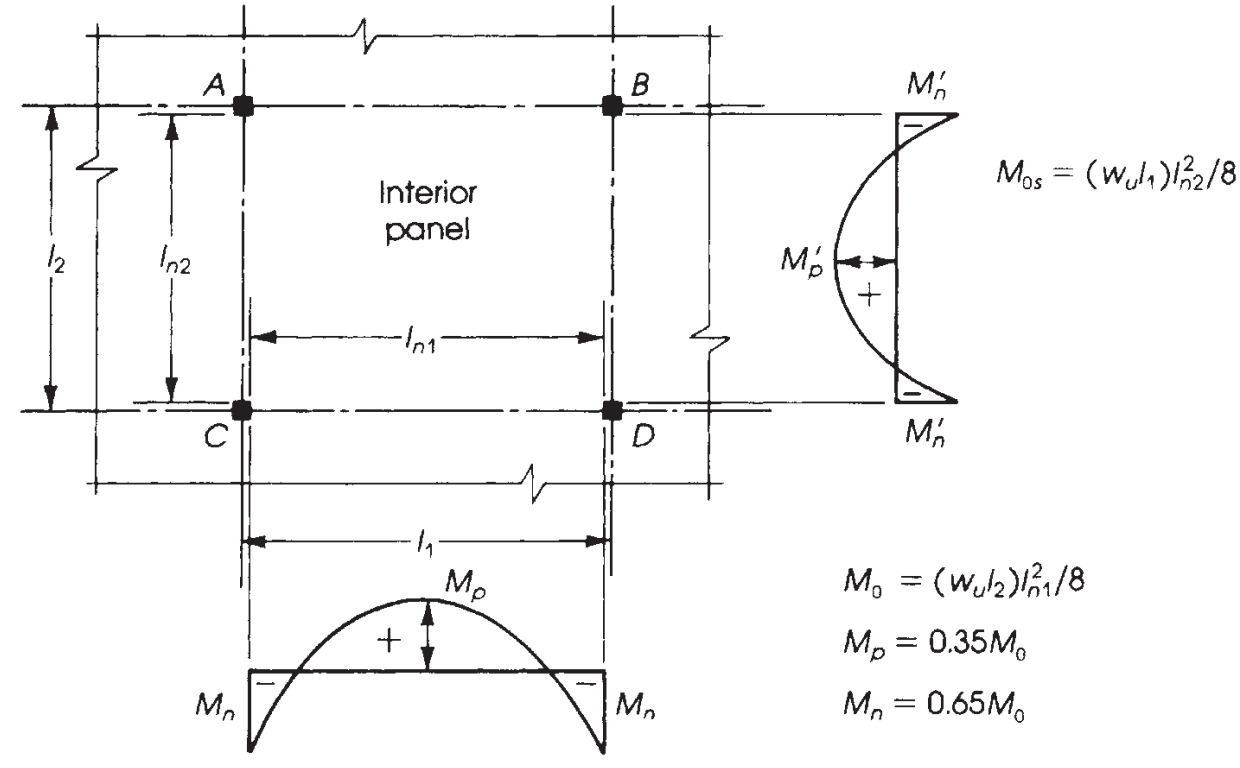
Figür 9. Bir iç panelde anların dağılımı. (Nadim Hassoun ve Akthem AI-Manaseer, “Yapısal Beton Teorisi ve Tasarımı”)
Tasarladığımız levhaya bağlı olarak momentlerin doğru dağılımını bilmek çok önemlidir.. Bu örnekte, aşağıdaki resimde son durumumuz var (şekil 9), “kiriş yok,” herhangi bir kiriş olmadan düz bir levhaya veya katı bir levhaya uygulanır, ne kenarda ne de destekler arasında.
Şekilde gösterilen beş durumdaki temel fark 9 dış panellerde atanacak moment kesirleridir, sondaki bağıl kısıtlamanın hesaplanacak değerleri değiştirdiği.
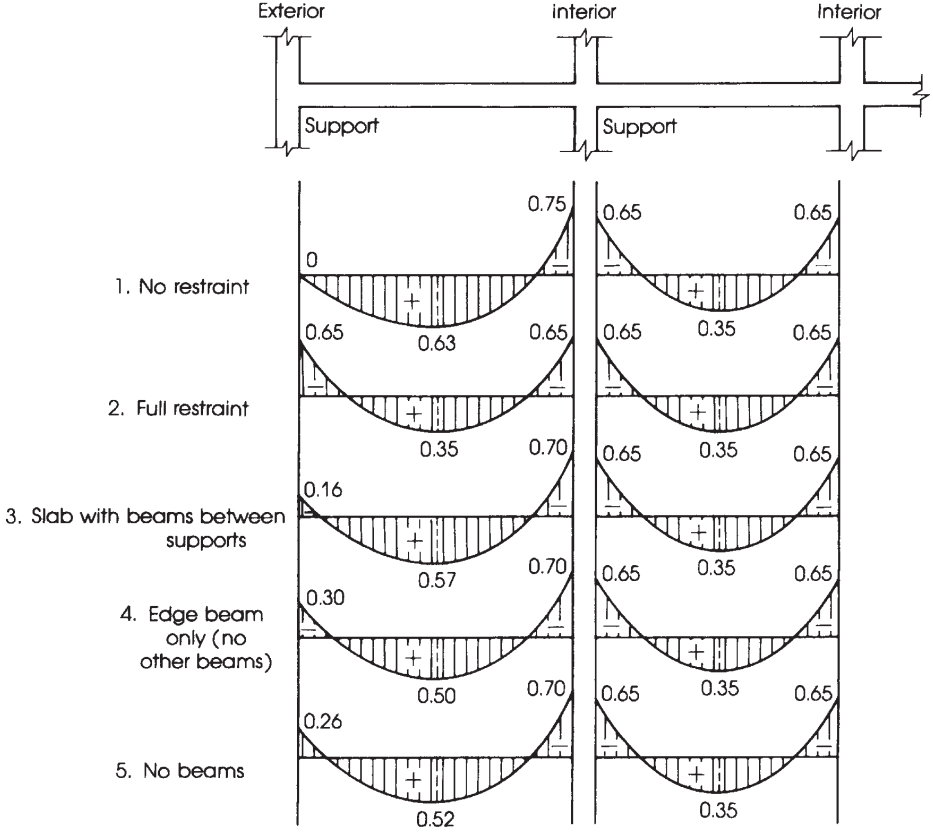
Figür 10. Toplam statik momentin negatif ve pozitif açıklık momentlerine dağılımı. (Nadim Hassoun ve Akthem AI-Manaseer, “Yapısal Beton Teorisi ve Tasarımı”)
Toplam çarpanlara ayrılmış momentin dağılımı \({M_0}\) negatif ve pozitif anlara açıklık başına.
Bir kere \({M_0}\) hesaplandı, her tasarım şeridinde momentlerin kesirlerini pozitif ve negatif olarak atamanın zamanı geldi, yani, sütun ve orta şeritler. Daha fazla netlik için, şekil 10 toplam momentin dağılımında dikkate alınacak uygun faktörün belirlenmesine yardımcı olur.
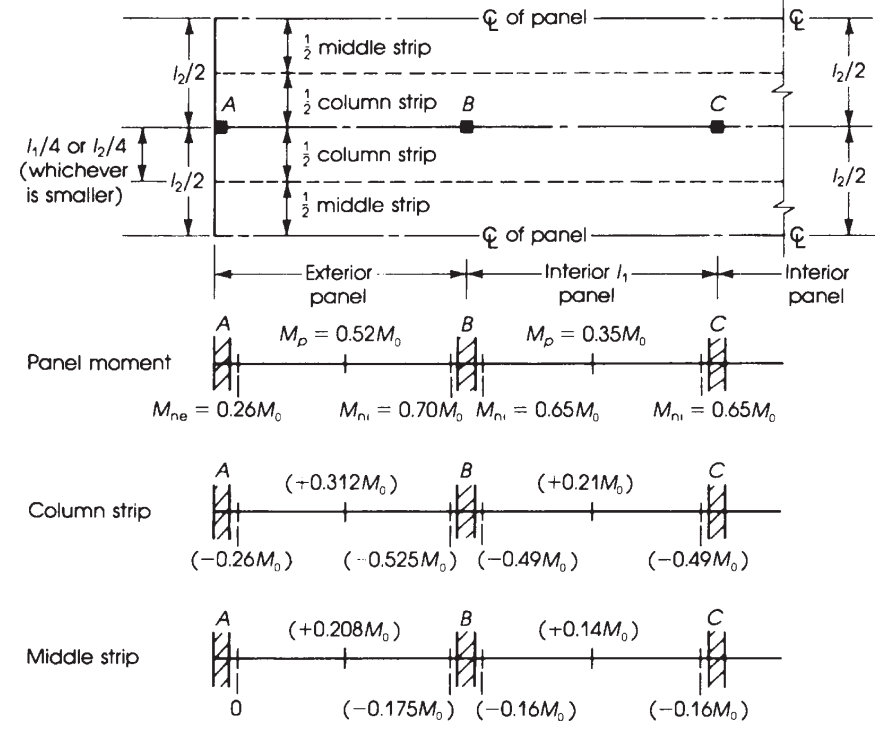
Figür 11. Düz döşemelerde eşdeğer rijit çerçevenin genişliği ve momentlerin dağılımı. (Nadim Hassoun ve Akthem AI-Manaseer, “Yapısal Beton Teorisi ve Tasarımı”)
Şekilde belirtilen önceki faktörleri kullanarak 10, aşağıdaki tabloda nihai anı elde ederiz.
boyuna yön: \({M_0 = 189.97 kN-m}\)
| açıklık (BU:Dış, DIR-DİR:İç mekan) | toplam an (kN-m) | Sütun şerit momenti (kN-m) | Orta şerit anı (kN-m) |
|---|---|---|---|
| Dış Negatif ES | 0.26M0=49.39 | 0.26M0=49.39 | 0 |
| pozitif ES | 0.52M0=98.78 | 0.31M0=58.89 | 0.21M0=39.89 |
| İç Mekan Negatif ES | 0.70M0=132.98 | 0.53M0=100.68 | 0.17M0=32.29 |
| Pozitif IS | 0.35M0=66.49 | 0.21M0=39.89 | 0.14M0=26.60 |
| negatif GP | 0.65M0=123.48 | 0.49M0=93.09 | 0.16M0=30.40 |
Bir kez dağıtılan an ile, Sıra levhaya konulacak çelik donatıyı belirlemeye geldi.. Yalnızca bir hesaplama geliştireceğiz ve ardından tüm sonuçları bir tabloya dönüştüreceğiz..
Sütun şeridindeki dış negatif yayılmadaki moment, \({M_u = 49.39 kN-m}\)
- Varsayılan gerilim kontrollü bölüm. \({\phi_f = 0.9}\)
- Sütun şeridi genişliği, \({b=2.0m}\)
- Çelik takviye alanı, \({A_s = frac{M_u}{\phi_ftimes 0.9dtimes fy}= frac{49.39kN-m}{0.9\zamanlar 0.9(0.17m)\zamanlar 420 MPa}=853.996 {mm}^ 2}\)
- \({\Bükülme momentleri kesitlerde her yönde hesaplanır{min} = 0.0018}\). Çelik minimum takviye alanı, \({bir_{s,min}=rho_{min}\çarpı bçarpı d = 0.0018 \çarpı 2,0m time 0,17m =612 {mm}^ 2}\). Şimdi, bölümün gerilim kontrollü davranıp davranmadığını kontrol edin.
- \({bir = frac{A_stimes f_y}{0.85\çarpı f’ckez b} = frac{853.996 {mm}^2kez 420 MPa}{0.85\zamanlar 25 MPakez 2.0m }= 8.439 mm}\)
- \({c = frac{a}{\beta_1}= frac{8.439 mm}{0.85} = 9,929 mm }\)
- \({\varepsilon_t = (\çatlamak{0.003}{c})\kere d – 0.003 = (\çatlamak{0.003}{9.929mm})\kez 170mm – 0.003 = 0.048 > 0.005 }\) Tamam mı!, gerilim kontrollü bir bölümdür!.
| açıklık(BU:Dış, DIR-DİR:İç mekan) | Kolon Şerit Momenti (kN-m) | \({bir_{s,kalk} ({mm}^ 2)}\) | \({bir_{s,min} ({mm}^ 2)}\) | \({a (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Dış Negatif ES | 49.39 | 853.996 | 612.0 | 8.439 | 9.929 | 0.048 > 0.005! |
| pozitif ES | 58.89 | 1018.259 | 612.0 | 10.063 | 11.839 | 0.040 > 0.005! |
| İç Mekan Negatif ES | 100.68 | 1740.844 | 612.0 | 17.204 | 20.24 | 0.022 > 0.005! |
| Pozitif IS | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.06 > 0.005! |
| negatif GP | 93.09 | 1609.607 | 612.0 | 15.907 | 18.714 | 0.024 > 0.005! |
Orta şeritteki dış pozitif yayılmadaki moment, \({M_u = 39.89 kN-m}\)
- Varsayılan gerilim kontrollü bölüm. \({\phi_f = 0.9}\)
- Orta şerit genişliği, \({b=2.0m}\)
- Çelik takviye alanı, \({A_s = frac{M_u}{\phi_ftimes 0.9dtimes fy}= frac{39.89kN-m}{0.9\zamanlar 0.9(0.17m)\zamanlar 420 MPa}=689.733 {mm}^ 2}\)
- \({\Bükülme momentleri kesitlerde her yönde hesaplanır{min} = 0.0018}\). Çelik minimum takviye alanı, \({bir_{s,min}=rho_{min}\çarpı bçarpı d = 0.0018 \çarpı 2,0m time 0,17m =612 {mm}^ 2}\). Şimdi, bölümün gerilim kontrollü davranıp davranmadığını kontrol edin.
- \({bir = frac{A_stimes f_y}{0.85\çarpı f’ckez b} = frac{689.766 {mm}^2kez 420 MPa}{0.85\zamanlar 25 MPakez 2.0m }= 6.816 mm}\)
- \({c = frac{a}{\beta_1}= frac{6.816 mm}{0.85} = 8.019 mm }\)
- \({\varepsilon_t = (\çatlamak{0.003}{c})\kere d – 0.003 = (\çatlamak{0.003}{8.019mm})\kez 170mm – 0.003 = 0.0605 > 0.005 }\) Tamam mı!, gerilim kontrollü bir bölümdür!.
| açıklık(BU:Dış, DIR-DİR:İç mekan) | Orta Şerit Momenti (kN-m) | \({bir_{s,kalk} ({mm}^ 2)}\) | \({bir_{s,min} ({mm}^ 2)}\) | \({a (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Dış Negatif ES | 0 | 0.00 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| pozitif ES | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.061 > 0.005! |
| İç Mekan Negatif ES | 32.29 | 558.322 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| Pozitif IS | 26.60 | 459.937 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| negatif GP | 30.40 | 525.642 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
Enlemesine yön: \({M_0 = 115.40 kN-m}\)
| açıklık (BU:Dış, DIR-DİR:İç mekan) | toplam an (kN-m) | Sütun şerit momenti (kN-m) | Orta şerit anı (kN-m) |
|---|---|---|---|
| Dış Negatif ES | 0.26M0=30.00 | 0.26M0=30.00 | 0 |
| pozitif ES | 0.52M0=60.00 | 0.31M0=35.77 | 0.21M0=24.23 |
| İç Mekan Negatif ES | 0.70M0=80.78 | 0.53M0=61.16 | 0.17M0=19.62 |
| Pozitif IS | 0.35M0=40.39 | 0.21M0=24.23 | 0.14M0=16.16 |
| negatif GP | 0.65M0=75.01 | 0.49M0=56.55 | 0.16M0=18.46 |
Bir kez dağıtılan an ile, şimdi levhaya yerleştirilecek çelik donatıyı belirleme zamanı. Yalnızca bir hesaplama geliştireceğiz ve ardından tüm sonuçları bir tabloya dönüştüreceğiz..
Sütun şeridindeki dış negatif yayılmadaki moment, \({M_u = 30.00 kN-m}\)
- Varsayılan gerilim kontrollü bölüm. \({\phi_f = 0.9}\)
- Sütun şeridi genişliği, \({b=2.0m}\)
- Çelik takviye alanı, \({A_s = frac{M_u}{\phi_ftimes 0.9dtimes fy}= frac{30.00kN-m}{0.9\zamanlar 0.9(0.17m)\zamanlar 420 MPa}=518.726 {mm}^ 2}\)
- \({\Bükülme momentleri kesitlerde her yönde hesaplanır{min} = 0.0018}\). Çelik minimum takviye alanı, \({bir_{s,min}=rho_{min}\çarpı bçarpı d = 0.0018 \çarpı 2,0m time 0,17m =612 {mm}^ 2}\). Şimdi, bölümün gerilim kontrollü davranıp davranmadığını kontrol edin.
- \({bir = frac{A_stimes f_y}{0.85\çarpı f’ckez b} = frac{518.726 {mm}^2kez 420 MPa}{0.85\zamanlar 25 MPakez 2.0m }= 6.048 mm}\)
- \({c = frac{a}{\beta_1}= frac{6.048 mm}{0.85} = 7,115 mm }\)
- \({\varepsilon_t = (\çatlamak{0.003}{c})\kere d – 0.003 = (\çatlamak{0.003}{7.115mm})\kez 170mm – 0.003 = 0.069 > 0.005 }\) Tamam mı!, gerilim kontrollü bir bölümdür!.
| açıklık(BU:Dış, DIR-DİR:İç mekan) | Kolon Şerit Momenti (kN-m) | \({bir_{s,kalk} ({mm}^ 2)}\) | \({bir_{s,min} ({mm}^ 2)}\) | \({a (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Dış Negatif ES | 30.00 | 518.726 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| pozitif ES | 35.77 | 618.494 | 612.0 | 6.112 | 7.191 | 0.068 > 0.005! |
| İç Mekan Negatif ES | 61.16 | 1057.509 | 612.0 | 10.451 | 12.295 | 0.038 > 0.005! |
| Pozitif IS | 24.23 | 418.958 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| negatif GP | 56.55 | 977.799 | 612.0 | 9.663 | 11.368 | 0.042 > 0.005! |
Orta şeritteki dış pozitif yayılmadaki moment, \({M_u = 24.23 kN-m}\)
- Varsayılan gerilim kontrollü bölüm. \({\phi_f = 0.9}\)
- Sütun şeridi genişliği, \({b=4.0m}\)
- Çelik takviye alanı, \({A_s = frac{M_u}{\phi_ftimes 0.9dtimes fy}= frac{24.23 kN-m}{0.9\zamanlar 0.9(0.17m)\zamanlar 420 MPa}=418.958 {mm}^ 2}\)
- \({\Bükülme momentleri kesitlerde her yönde hesaplanır{min} = 0.0018}\). Çelik minimum takviye alanı, \({bir_{s,min}=rho_{min}\çarpı bçarpı d = 0.0018 \çarpı 4,0m time 0,17m =1224 {mm}^ 2}\). Şimdi, bölümün gerilim kontrollü davranıp davranmadığını kontrol edin.
- \({bir = frac{A_stimes f_y}{0.85\çarpı f’ckez b} = frac{1224 {mm}^2kez 420 MPa}{0.85\zamanlar 25 MPakez 4.0m }= 6.048 mm}\)
- \({c = frac{a}{\beta_1}= frac{6.048 mm}{0.85} = 7.115 mm }\)
- \({\varepsilon_t = (\çatlamak{0.003}{c})\kere d – 0.003 = (\çatlamak{0.003}{7.115mm})\kez 170mm – 0.003 = 0.069 > 0.005 }\) Tamam mı!, gerilim kontrollü bir bölümdür!.
| açıklık(BU:Dış, DIR-DİR:İç mekan) | Orta Şerit Momenti (kN-m) | \({bir_{s,kalk} ({mm}^ 2)}\) | \({bir_{s,min} ({mm}^ 2)}\) | \({a (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Dış Negatif ES | 0.00 | 0.00 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| pozitif ES | 24.23 | 418.958 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| İç Mekan Negatif ES | 19.62 | 339.247 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| Pozitif IS | 16.16 | 279.420 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| negatif GP | 18.46 | 319.189 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
SkyCiv'de yeniyseniz, Kaydolun ve yazılımı kendiniz test edin!
SkyCiv S3D Tasarım Modülü
Bu bölümde, tasarım sonucunu, SkyCiv'de bulunan plaka tasarımı için modülü kullanarak açıklıyoruz. Yapının nasıl modelleneceğini ve analiz edileceğini açıklamıyoruz. (bunlar için, belgelerimizdeki bu konuyla ilgili makalelere bakın: SkyCiv'de bir yapı nasıl modellenir??, Bina modelime yükler nasıl uygulanır?? ve Doğrusal elastik analiz nasıl yapılır?)
Doğru bir tasarım sonucu elde etmek için levhalara ince bir ağ uygulamak uygundur.. Daha fazla netlik için lütfen aşağıdaki resme bakın.
Figür 12. Plakalara uygulanan daha ince ağ
Bir sonraki adım, tasarım modülünü çalıştırmak ve optimize edilmiş çelik donatı alanını hesaplayan seçenekleri seçmektir..
Figür 13. Tasarım optimizasyonundan önce döşeme betonu özellikleri tanımı.
Figür 14 plakanın yerel eksen yönünü temsil eder. Çünkü yerel eksen 3 aşağı doğru, NS “üst” alt mı, ve “alt” zirve olacak, böylece verileri tasarımdan doğru bir şekilde almak.
Bir diğer önemli gerçek, döşeme ağ boyutudur.; 500mm x 500mm plan ölçülerinde levha kare elemandır.. SkyCiv S3D, donatı alanını sonlu eleman başına entegre bir değer olarak verir. Böylece, bir kolonun veya orta şeridin toplam donatı alanını elde etmek istiyorsak, analiz edilen şerit genişliğini toplayan eleman sayısından ortalama değeri hesaplamamız gerekiyor. Örneğin, sütun şeridi için, dört unsur dikkate alınacak (4×0.5m = 2m).
Figür 14. Döşeme örneğinde yerel eksen oryantasyonu.
İlk, eksende boyuna yönde gerekli donatı alanını analiz ediyoruz 1.
Sütun Şeridi
- Dış olumsuz an (üst takviye): \({bir_{s,üst} =(119.09\zamanlar 2 + 952.72 + 833.64 )\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 1012.27 {mm}^ 2}\)
- Dış olumlu an (alt takviye): \({bir_{s,bot} = 4*463.90 \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 927.80 {mm}^ 2}\)
- Dış iç olumsuz an (üst takviye): \({bir_{s,üst} =(1071.82\zamanlar 2 +714.54 \zamanlar 2 )\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 1786.36 {mm}^ 2}\)
- İç pozitif an(alt takviye): \({bir_{s,bot} = 4*309.27 \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 618.54 {mm}^ 2}\)
- İç olumsuz an (üst takviye): \({bir_{s,üst} =(714.54\zamanlar 2 +952.73 \zamanlar 2 )\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 1667.27 {mm}^ 2}\)
Orta Şerit
- Dış olumsuz an (üst takviye): \({bir_{s,üst} =(119.09\zamanlar 4)\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 238.18 {mm}^ 2}\)
- Dış olumlu an (alt takviye): \({bir_{s,bot} = (463.90\zamanlar 2 +412.36 \zamanlar 2 ) \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 876.26 {mm}^ 2}\)
- Dış iç olumsuz an (üst takviye): \({bir_{s,üst} =(357.27\zamanlar 2 +476.36 \zamanlar 2 )\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 833.63 {mm}^ 2}\)
- İç pozitif an(alt takviye): \({bir_{s,bot} = 4*257.72 \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 515.44 {mm}^ 2}\)
- İç olumsuz an (üst takviye): \({bir_{s,üst} =(357.27\zamanlar 2 +476.36 \zamanlar 2 )\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 833.63 {mm}^ 2}\)
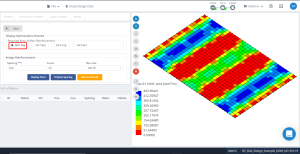
Figür 15. Yönde optimizasyon sonuçları “1” ve üst taraf (Alt taraf, aslında).
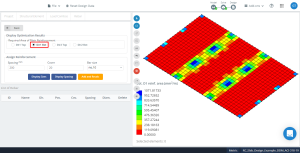
Figür 16. Yönde optimizasyon sonuçları “1” ve alt taraf (Üst taraf, aslında).
En sonunda, eksende enine yön boyunca gerekli donatı alanını analiz ediyoruz 2.
Sütun Şeridi
- Dış olumsuz an (üst takviye): \({bir_{s,üst} =(91.55\zamanlar 2 + 457.73 + 549.28 )\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 595.055 {mm}^ 2}\)
- Dış olumlu an (alt takviye): \({bir_{s,bot} = (269.68\zamanlar 3+239.72) \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 524.38 {mm}^ 2}\)
- Dış iç olumsuz an (üst takviye): \({bir_{s,üst} =(823.92\zamanlar 2 +549.28 +457.73)\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 1327.43 {mm}^ 2}\)
- İç pozitif an(alt takviye): \({bir_{s,bot} = (179.79\zamanlar 3+149.82) \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 344.60 {mm}^ 2}\)
- İç olumsuz an (üst takviye): \({bir_{s,üst} =(823.92\zamanlar 2 +549.28 +457.73)\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 1327.43 {mm}^ 2}\)
Orta Şerit
- Dış olumsuz an (üst takviye): \({bir_{s,üst} =(183.09\çarpı 2+91,55kez 6)\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 457.74 {mm}^ 2}\)
- Dış olumlu an (alt takviye): \({bir_{s,bot} = (209.75\zamanlar 2 +179.79 \zamanlar 2 +149.82 \zamanlar 4) \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 689.18{mm}^ 2}\)
- Dış iç olumsuz an (üst takviye): \({bir_{s,üst} =(274.64\çarpı 2+91,55kez 6)\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 549.29 {mm}^ 2}\)
- İç pozitif an(alt takviye): \({bir_{s,bot} = (119.86\zamanlar 4 + 89.89\zamanlar 4) \çatlamak{{mm}^ 2}{m}\çarpı 0.50m = 419.50 {mm}^ 2}\)
- İç olumsuz an (üst takviye): \({bir_{s,üst} =(274.64\çarpı 2+91,55kez 6 )\çatlamak{{mm}^ 2}{m} \çarpı 0.50m = 549.29 {mm}^ 2}\)
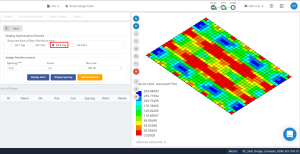
Figür 17. Yönde optimizasyon sonuçları “2” ve üst taraf (Alt taraf, aslında).
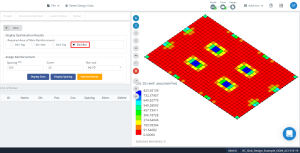
Figür 18. Yönde optimizasyon sonuçları “2” ve alt taraf (Üst taraf, aslında).
Sonuç karşılaştırması
Aşağıdaki tabloda DDM için sonuçlar gösterilmektedir (“Doğrudan Tasarım Yöntemi”) ve S3D çelik inşaat demiri optimizasyonu.
| açıklık (BU:Dış, DIR-DİR:İç mekan) | Sütun Şeridi (S3D Tasarım) \({Olarak ({mm}^ 2)}\) | Sütun Şeridi (ACI-318 DDM) \({Olarak ({mm}^ 2)}\) | % fark | Orta Şerit (S3D Tasarım) \({Olarak ({mm}^ 2)}\) | Orta Şerit (ACI-318 DDM) \({Olarak ({mm}^ 2)}\) | % fark |
|---|---|---|---|---|---|---|
| Dış Negatif ES | 1012.27 | 853.996 | 15.636 | 238.18 | 0 (612.0) | 100.00 |
| pozitif ES | 927.80 | 1018.259 | 9.75 | 876.26 | 689.733 | 21.287 |
| İç Mekan Negatif ES | 1786.36 | 1740.844 | 2.48 | 833.63 | 558.322 (612.0) | 26.586 |
| Pozitif IS | 618.54 | 689.733 | 11.51 | 515.44 | 459.937 (612.0) | 18.734 |
| negatif GP | 1667.27 | 1609.607 | 3.459 | 833.63 | 525.642 (612.0) | 26.586 |
Enlemesine yön
| açıklık (BU:Dış, DIR-DİR:İç mekan) | Sütun Şeridi (S3D Tasarım) \({Olarak ({mm}^ 2)}\) | Sütun Şeridi (ACI-318 DDM) \({Olarak ({mm}^ 2)}\) | % fark | Orta Şerit (S3D Tasarım) \({Olarak ({mm}^ 2)}\) | Orta Şerit (ACI-318 DDM) \({Olarak ({mm}^ 2)}\) | % fark |
|---|---|---|---|---|---|---|
| Dış Negatif ES | 595.055 | 518.726 | 12.827 | 457.74 | 0 (1224) | 100.00 |
| pozitif ES | 524.38 | 618.494 | 17.948 | 689.18 | 418.958 | 39.209 |
| İç Mekan Negatif ES | 1327.43 | 1057.509 | 20.334 | 549.29 | 339.247 | 38.239 |
| Pozitif IS | 344.60 | 418.958 | 21.578 | 419.50 | 279.42 | 33.392 |
| negatif GP | 1327.43 | 977.799 | 26.339 | 549.29 | 319.189 | 41.891 |
Sonuç
Bu makalede, plaka tasarımı için SkyCiv modülünün ACI-318-19 koduna göre levhayı bükmek için çelik donatıyı hesapladığını gösterdik.. Kolon şeritlerindeki analizden elde edilen sonuçların karşılaştırılması, göreceli sertlikleri nedeniyle nerede, anlar oldukça yoğun, elle hesaplamalar ve S3D ile optimizasyon arasındaki farklar 10 – 15%. Bu pratiklik, analiz ve tasarım prosedürleri arasında mükemmel bir eşleşme olduğunu gösterir..
Orta şeritler için, Sonuçlar biraz daha farklıdır çünkü kod yalnızca karşılık gelen sütun şeritlerini aldıktan sonra kalan anı atar.. Bu, yazılımın analiziyle karşılaştırdığımızda maçı etkileyecektir., hangisi daha doğru.
SkyCiv'de Yeni? Kaydolun ve yazılımı kendiniz deneyin!


