Yalıtılmış bir temel tasarlamak için gerekli hesaplamalara yönelik bir kılavuz (İÇİNDE 1992 & İÇİNDE 1997)

Temel, kolon ve duvar kuvvetlerini taşıyıcı zemine aktaran temel bir yapı sistemidir.. Zemin özelliklerine ve bina yüklerine bağlı olarak, Mühendis, yapıyı sığ veya derin bir temel sistemi üzerinde desteklemeyi seçebilir³.

SkyCiv Vakfı, Eurocode 2¹ ve Eurocode'a uygun izole temel tasarımını içerir 7².

SkyCiv’in Temel Tasarım yazılımını denemek ister misiniz?? Aracımız, kullanıcıların herhangi bir indirme veya kurulum yapmadan Temel Tasarım hesaplamaları yapmasına olanak tanır!

Temel Tasarım Hesaplayıcı

İzole Temelin Tasarım Parametreleri

SkyCiv'de sunulan hesaplamalar EN'ye dayalı kuralcı yöntemi kullanır 1997, Temelin hizmet verilebilirlik sınır durumuna göre boyutlandırılması için varsayılan güvenli taşıma basıncının kullanıldığı ve ardından nihai sınır durumuna dayalı ayrıntılı yapısal tasarımın yapıldığı yer.

Boyut Gereksinimleri

Yalıtılmış bir temelin boyutlarını belirlemek için, karakteristik eylemler, Kalıcı/Ölü gibi (Q), Değişken/Canlı (Ql), Rüzgar (Qw), Sismik (Qe), Kullanılabilirlik sınır durumu için vb. uygulanacaktır. Kritik yükleme düzenlemesi/kombinasyonu tasarım yükü olarak kabul edilecektir., ve Denklemde gösterildiği gibi izin verilen toprak basıncıyla karşılaştırılır 1. Bu örnek yalnızca üniform toprak basıncıyla sınırlıdır.

\(\Metin{q}_{\Metin{a}} = frac{\Metin{P}_{\Metin{n}}}{\Metin{Bir}} \sağ ok \) Denklem 1

nerede:
q_a = izin verilen toprak basıncı
P_n = yüklenmemiş tasarım yükü
A = Temel alanı

Denklemden 1, q_a ile değişiyorlar Bir.

\(\Metin{Bir} = frac{\Metin{P}_{\Metin{n}}}{\Metin{q}_{\Metin{a}}} \sağ ok \) Denklem 1a

Bu noktada, temel boyutları gerekli alan boyutundan geriye doğru hesaplanabilir, Bir.

Eğilme

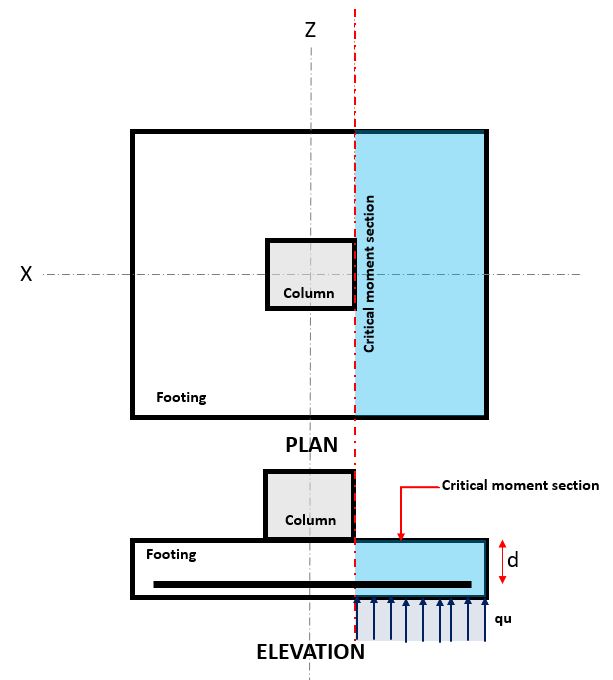
Figür 1. Kritik Eğilme Bölümü

NS Eğilme sınır durumu şu anda meydana gelir: Kritik Eğilme Bölümü, temelin üstünde sütunun yüzünde bulunur (Şekle bakın 1).

NS Eğilme Talebi, veya M_ED Kritik Eğilme Bölümünde bulunur (mavi tarama alanı) Şekilde gösterilen 1, ve Denklem kullanılarak hesaplanır 2.

\( \Metin{M}_{sen} = text{q}_{sen} \kez kaldı ( \çatlamak{l_{x}}{2} – \çatlamak{c_{x}}{2} \sağ ) \kere l_{ile} \kez kaldı ( \çatlamak{\çatlamak{l_{x}}{2} – \çatlamak{c_{x}}{2} }{2} \sağ ) \sağ ok \) Denklem 2

nerede:
q_sen = faktörlü toprak basıncı, kPa
l_x = x ekseni boyunca temel boyutu, mm
l_ile = z ekseni boyunca temel boyutu, mm
c_x = x ekseni boyunca sütun boyutu, mm

NS Eğilme Kapasitesi, veya Mkapasite Denklem kullanılarak hesaplanır 3.

\(\Metin{M}_{kapasite} = frac{1}{\gama_{S,puan}} \kere f_{yk} \kere A_{s} \kez kaldı( d – \çatlamak{s}{2} \sağ) \sağ ok \) Denklem 3

nerede:
c_S,puan = Takviye çeliği için kısmi faktör
l_x = x eksenine paralel temel boyutu, mm
l_ile = z eksenine paralel temel boyutu, mm
d = aşırı sıkıştırma elyafından uzunlamasına gerilim takviyesinin ağırlık merkezine olan mesafe, mm
Bir_s = takviye alanı, mm²
s = eşdeğer dikdörtgen gerilim bloğunun derinliği, mm
fyk = takviye kuvveti, MPa

Tek yönlü Makas

NS tek yönlü kesme sınır durumu, Ayrıca şöyle bilinir kiriş kesme, uzakta bulunur “d” bir sütunun yüzünden, Kritik Kesme Düzleminde (Şekle bakın 2),

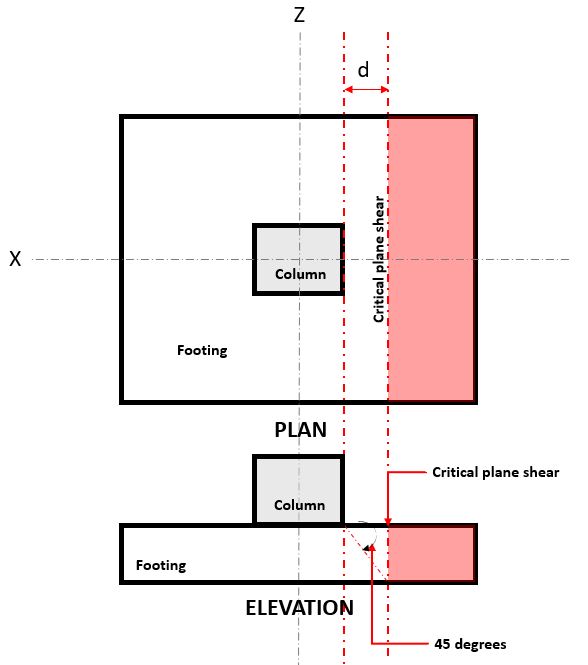
Figür 2. Tek Yönlü Makasın Kritik Düzlem Kayması

NS Tek yön Kesme Talep veya V _ED , temelin alanın bulunduğu sütundan uzağa konsolda olduğu varsayılarak hesaplanır. (kırmızı) Şekilde gösterilen 2.

NS Tek Yönlü Kesme Kapasitesi veya V _Yol,c Nihai Sınır Durumunda kesme direnci olarak tanımlanır (kesme takviyesi gerekmediğinde) ve Denklem kullanılarak hesaplanır 6 başına İÇİNDE 1992, Bölüm 6.2.2.

\(\Metin{V }_{\Metin{Yol,c}} = (\Metin{C}_{\Metin{Yol,c}} \çarpı k time (100 \kere rho_{1} \kere metin{f}_{\Metin{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}})^{\çatlamak{1}{3}}) \kere metin{b}_{\Metin{w}} \kere metin{d} \sağ ok \) Denklem 6 (İÇİNDE 1992 Eşitlik. 6.2.a)

minimum ile

\(\Metin{V }_{\Metin{Yol,c}} = (0.035 \çarpı k^{\çatlamak{3}{2}} \kere metin{f}_{\Metin{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}}^{\çatlamak{1}{2}}) \kere metin{b}_{\Metin{w}} \kere metin{d} \sağ ok \) Denklem 9 (İÇİNDE 1992 Eşitlik. 6.2.b)

nerede:
C_Yol,c = önerilen değer 0,18/γ_C
k = katsayısı 1 + √(200/d) ≤ 2.0
r₁ = bir_sl / b_wd ≤ 0.02
f_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.} = belirtilen beton dayanımı, MPa
b_w = temelin genişliği, mm
d = aşırı sıkıştırma elyafından uzunlamasına gerilim takviyesinin ağırlık merkezine olan mesafe, mm

Kesme Talebi ve Kesme Kapasitesi EN Nihai Sınır Durumunu karşılayacak şekilde doğrulanmalıdır 1990:

\(\Metin{E}_{\Metin{d}} \leq text{R}_{\Metin{d}} \sağ ok \) Denklem 4 (İÇİNDE 1990 6.4.1)

SkyCiv Vakfı, Denklem uyumlu 4, tek yönlü kayma birimi oranını hesaplar (Denklem 7) Kesme Kapasitesi yerine Kesme Talebini alarak.

\( \Metin{Birlik Oranı} = frac{\Metin{Kesme Talebi}}{\Metin{Kesme Kapasitesi}} \sağ ok \) Denklem 7

İki yönlü Makas

NS İki yönlü Makas sınır durumu, Ayrıca şöyle bilinir delme makası, kritik bölümü bir mesafeye uzatır “2d” kolonun yüzünden ve kolonun çevresinden. Kritik Kayma Düzlemi, temelin bu bölümünde bulunur (Şekle bakın 3).

Figür 3. İki yönlü kesme için Kritik Kesme Düzlemi

NS İki yolTalebi duymak veya V _ED Kritik Kesme Düzleminde meydana gelir, Şekilde gösterilen 3, göre İÇİNDE 1992, Bölüm 6.4.2.

NS Kesme Kapasitesi veya V _Yol,c, tek yönlü kesme kapasitesine benzer (kesme takviyesi gerekmediğinde), EN temel alınarak hesaplanır 1992 Bölüm 6.2.2 (Denklem'e bakın. 8).

\(\Metin{V }_{\Metin{Yol,c}} = (\Metin{C}_{\Metin{Yol,c}} \çarpı k time (100 \kere rho_{1} \kere metin{f}_{\Metin{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}})^{\çatlamak{1}{3}}) \kere metin{sen}_{\Metin{1}} \kere metin{d} \sağ ok \) Denklem 8 (İÇİNDE 1992 Eşitlik. 6.2.a)

minimum ile

\(\Metin{V }_{\Metin{Yol,c}} = (0.035 \çarpı k^{\çatlamak{3}{2}} \kere metin{f}_{\Metin{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}}^{\çatlamak{1}{2}}) \kere metin{sen}_{\Metin{1}} \kere metin{d} \sağ ok \) Denklem 9 (İÇİNDE 1992 Eşitlik. 6.2.b)

 

nerede:
sen₁ = temel kontrol çevresi, mm
Tek Yönlü Kesme Kapasitesinde benzer şekilde tanımlanan diğer değişkenler.

Genel olarak, Kesme Talebi ve Kesme Kapasitesi, EN Nihai Sınır Durumunu karşılamak için aşağıdaki denklemi karşılamalıdır. 1990:

\(\Metin{E}_{\Metin{d}} \leq text{R}_{\Metin{d}} \sağ ok \) Denklem 4 (İÇİNDE 1990 6.4.1)

SkyCiv Vakfı, Denklem ile uyumlu 4, iki yönlü kayma birim oranını hesaplar (Denklem 10) Kesme Kapasitesi yerine Kesme Talebini alarak.

\( \Metin{Birlik Oranı} = frac{\Metin{Kesme Talebi}}{\Metin{Kesme Kapasitesi}} \sağ ok \) Denklem 10

 

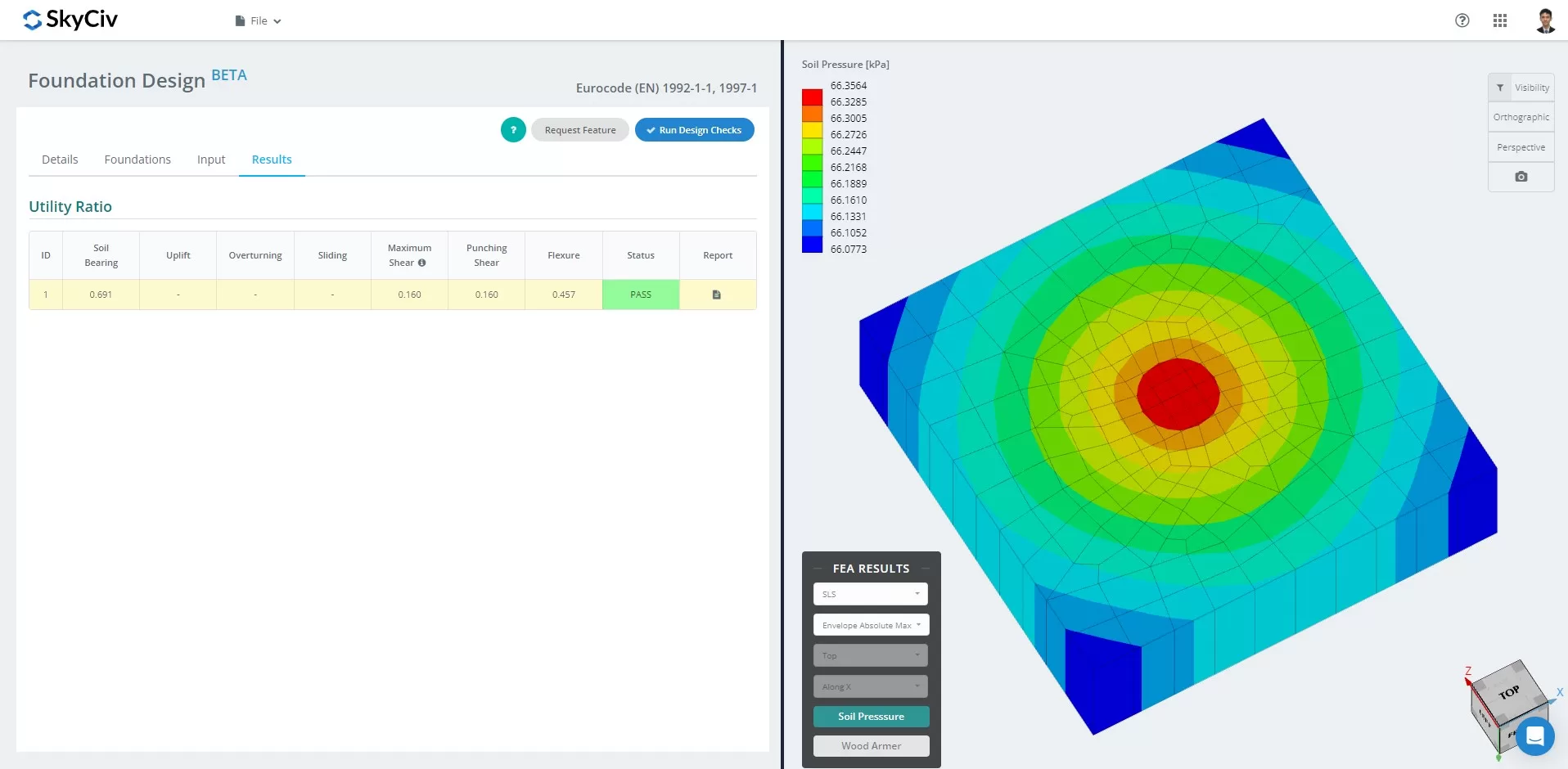
FEA ile YENİ SkyCiv Vakfı

Mart ayı itibarıyla 2024, Temel Tasarım Modülü Sonlu Elemanlar Analizini entegre etmiştir (ÇİRKİN) çözücüyü yeteneklerine göre. Bu yeni özellik, kullanıcıların bir yandan EN tarafından belirtilen tüm yapısal kontrolleri gerçekleştirirken bir yandan da derinlemesine toprak basıncı ve ahşap armer analizleri yapmasına olanak tanır. 1992 ve 1997, yukarıda belirtilen tüm doğrulamalar dahil. FEA Sonuçlarının Özeti kapsamlı rapora dahil edilmiştir.

 

Ücretsiz Beton Temel Hesaplayıcı

Temellerin temellerini tasarlamak için SkyCiv Ücretsiz Beton Temel Hesaplayıcıyı deneyin, birleşik temeller, beton yığınları, beton pedler, ve dahası.

Temel Tasarım Hesaplayıcı