Kazık Kapasitesinin Tahmini
Kazığın taşıyabileceği nihai eksenel yükü belirlemek için kazık yük taşıma kapasitesinin tahmin edilmesi gereklidir.. Kazığın nihai yük kapasitesi (Tek bir yığının nihai yük taşıma kapasitesi nasıl hesaplanır?) uç taşıma kapasitesinin toplamına eşittir (Qp) ve sürtünme direnci (Sorular), Şekil ile temsil edilir. 1 ve denklem. 1. Yayınlanmış çok sayıda çalışma ve uygulama, yığının taşıma kapasitesini ve sürtünme direncini belirler.. Bu makale, nihai kazık kapasitesini tahmin etmek için çeşitli yöntemlere odaklanmaktadır..
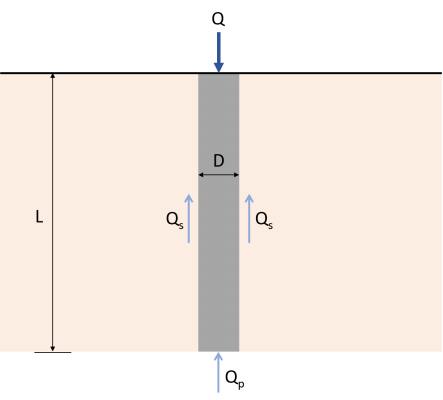
\( {Q}_{sen} = {Q}_{p} + {Q}_{s} \) (1)
Qsen : Nihai yük taşıma kapasitesi
Qp : Uç yatak yük kapasitesi
Qs : Cilt sürtünme direnci
Q için evrensel denklemlerp Tek bir yığının nihai yük taşıma kapasitesi nasıl hesaplanır?s
\( {Q}_{p} = {Bir}_{p} \zamanlar {q}_{p} \) (2)
\( {q}_{p} = (c \times {N}_{c}) + (q’ \zamanlar {N}_{q}) + (\gamma \times D \times {N}_{\gama}) \) (3)
\( {Q}_{p} = {Bir}_{p} \zamanlar[ (c \times {N}_{c}) + (q’ \zamanlar {N}_{q}) ] \) (4)
Yığının toplam sürtünme direnci, uzunluğu boyunca gelişmiş olan, bu denklem kullanılarak hesaplanabilir:
\( {Q}_{s} Kazıkların yüzey sürtünme direnci, kazık uzunluğu boyunca geliştirilir (Kazıkların yüzey sürtünme direnci, kazık uzunluğu boyunca geliştirilir) \) (5)
p: yığının çevresi
L: Üzerinde p ve f'nin alındığı artımlı yığın uzunluğu
f: Herhangi bir derinlikte birim sürtünme direnci
Qp'yi Tahmin Etme Yöntemleri
Meyerhof Yöntemi
Kumlu toprak
Meyerhof'a göre, birim nokta direnci (qp) kumdaki kazıkların sayısı genellikle gömme uzunluğuyla birlikte artar ve gömme oranı maksimum değerine ulaşıncaya kadar (L/D) kritik bir değere ulaşır. Kritik gömme oranı (L/D)sonucu AISI S100-12'ye göre hesaplayacaktır genellikle değişir 16 -e 18. Bu yöntemde, kumdaki yığınların kohezyonun sıfır olduğu varsayılır (c ≈ 0), ve birim nokta direnci sınır noktası direncini aşmamalıdır (ql), Denklem tarafından verilen. 7. Taşıma kapasitesi faktörü (Nq) değerler, taşıyıcı tabakanın toprak sürtünme açısı ile doğru orantılıdır (Tablo 1). Meyerhof'un teorisine dayanarak, Q için evrensel denklemp (Denk.4) basitleştirilebilir:
\( {Q}_{p} = {Bir}_{p} \zamanlar (q’ \zamanlar {N}_{q}) \leq ({Bir}_{p} \zamanlar {q}_{l}) \) (6)
\( {q}_{l} = 0.5 \zamanlar {p}_{a} \zamanlar {N}_{q} \kere bronzlaşmak (\önceki denklemlerde) \) (7)
ql : Sınır noktası direnci
pa: Atmosferik basınç (≈100 kN/m2)
\( \phi’\): Yığının ucunda etkili zemin sürtünme açısı
Tablo 1: N'nin enterpolasyonlu değerleriq (Meyerhof'un teorisi)
Killi Toprak
Denklem 4 kil veya kohezyonlu zeminlerdeki kazıkların uç taşıma kapasitesini de hesaplayabilir (φ ≈ 0). Zemin sürtünme açısı ihmal edildiğinden ve taşıma gücü faktörü (Nc) sabit bir değere sahiptir 9 kohezyonlu zeminler için, Denklem 4 şu şekilde yazılabilir::
\( {Q}_{p} = {Bir}_{p} \times c \times {N}_{c} = 9 \times c \times {Bir}_{p} \) (8)
Vesic Yöntemi
Vesic'in kumlu veya killi zeminlerde uç taşıma kapasitesini hesaplama yöntemi, boşlukların genişlemesi teorisine dayanmaktadır..
Kumlu toprak
Teorisine dayanarak, Kumdaki kazıkların uç taşıma kapasitesi aşağıdaki denklemler kullanılarak tahmin edilebilir.:
\( {Q}_{p} = {Bir}_{p} \times \bar{\sigma'}_{Ö} \zamanlar {N}_{\sigma} \) (9)
\(\bar{\sigma'}_{Ö} = frac{1 + (2 \zamanlar {K}_{Ö})}{3} \times q’\) (10)
\( {K}_{Ö} = 1 – sin \phi’\) (11)
\( {N}_{\sigma} = frac{3 \zamanlar {N}_{q}}{1 + (2 \zamanlar {K}_{Ö})} \) (12)
\(\bar{\sigma'}_{Ö} \) : Yığın noktası seviyesindeki ortalama etkin normal zemin gerilimi
Dır-dir: Dinlenme halindeki toprak basıncı katsayısı
Ns: Rulman kapasitesi faktörü
Killi Toprak
Meyerhof'un yöntemiyle aynı, Eşitlik. 4 kildeki kazıkların uç taşıma kapasitesini hesaplamak için de geçerlidir.. ancak, taşıma kapasitesi faktörünün değeri (Nc) katılık indeksinin bir faktörüdür (benr). Boşlukların genişlemesi teorisine göre, Nc ve benr tarafından tahmin edilebilir:
\( {N}_{c} = (\çatlamak{4}{3}) \zamanlar [ln({ben}_{r}) + 1] + \çatlamak{\pi}{2} + 1 \) (13)
\( {ben}_{r} = frac{{E}_{s}}{3 \çarpı c} \) (φ ≈ için 0)(14)
benr: rijitlik indeksi
Es: Toprağın elastisite modülü
Coyle ve Castello'nun Yöntemi (Kumlu toprak)
Dayalı 24 kumda çakma kazıkların büyük ölçekli saha yükü testleri, Coyle ve Castello, kazıkların uç taşıma kapasitesinin Denklem 15 kullanılarak hesaplanabileceğini öne sürdü.. Taşıma gücü faktörü değerleri (Nq) her iki gömme oranının da bir faktörüdür (L/D) ve toprak sürtünme açısı (Phi'), Şekilde gösterildiği gibi. 2
\( {Q}_{p} = {Bir}_{p} \zamanlar (q’ \zamanlar {N}_{q}) \) (15)
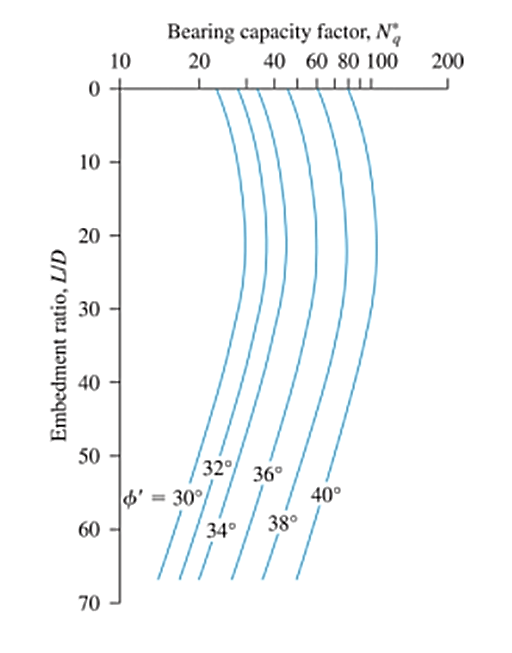
Figür 2: Nq'nin L/D ile değişimi & hesaplamalar ayrıca açık ve ayrıntılı PDF raporlama ile birlikte gelir’ (Coyle'dan sonra yeniden çizildi & Castello, 1981)
Kaynak: İstinat duvarına etki eden yanal toprak basıncı, duvar toprak kütlesine itildiğinde pasif kabul edilir., braja. İstinat duvarına etki eden yanal toprak basıncı, duvar toprak kütlesine itildiğinde pasif kabul edilir. (7th Baskı, s.564)
Q'ları Tahmin Etme Yöntemleri
Kumdaki Kazıkların Sürtünme Dayanımı
Kumdaki kazıkların birim sürtünme direnci, denklemde gösterildiği gibi. 5, hesaplanması oldukça zor olan birden fazla faktörü göz önünde bulundurur. Toprak basıncı katsayısını içerir (K) & zemin kazık sürtünme açısı, Her ikisi de hangi yaklaşımın kullanılacağına veya mevcut toprak verilerine bağlı olarak değişen değerlere sahiptir..
\( f = K\times {\sigma}_{Ö}’ \kere bronzlaşmak (\delta) \) (15)
K: Etkili toprak basıncı katsayısı
σ’Ö: Ele alınan derinlikte etkili düşey gerilim
NS: Zemin-kazık sürtünme açısı
Aşağıda, etkili toprak basıncı katsayısını ve toprak sürtünme açısı değerlerini tahmin etmenin farklı yolları verilmiştir.. Bu değişkenler zemin sürtünme açısının bir faktörüdür. (Phi') veya kazık tipi.
Etkili toprak basıncı katsayısı
Toprak, kazık yüzeyine yanal toprak basıncı uygular.. Kararlılık için tasarım veya analiz üzerindeki bu baskıyı hesaba katmak gerekir.. Aşağıda, kazıkların kumdaki birim sürtünme direncini hesaplamak için toprak basıncı katsayılarını belirlemenin farklı yolları verilmiştir..
Denklemin son teriminin sonuç değeri 7.2
| K = Efektif toprak basıncı katsayısı | Sıkıştırma | yükseltme |
|---|---|---|
Tablo 2: toprak basıncı katsayısı, K (Denklemin son teriminin sonuç değeri 7.2)
Ortalama K Yöntemi
Toprak basıncı katsayısı (K) durağan toprak basıncı katsayısının ortalaması alınarak da değerlendirilebilir (K0), aktif toprak basıncı (Ka), ve pasif toprak basıncı (Kp), Denklemlerden gösterildiği gibi 16-19.
\( K =\frac{{K}_{0} + {K}_{a} + {K}_{p}}{3} \) (16)
\( (K)_{0} =1 – sin \phi \) (17)
\( (k_{a} =1 – {bronzlaşmak}^{2}( \çatlamak{45 – \fi}{2}) \) (18)
\( (k_{p} =1 + {bronzlaşmak}^{2}( \çatlamak{45 + \fi}{2}) \) (19)
Mansur ve Avcı (1970)
Farklı saha yükü testi sonuçlarına göre, Mansur ve Hunter, toprak basıncı katsayısı değerlerini karşılık gelen kazık tipleriyle sonuçlandırmıştır..
| K = Efektif toprak basıncı katsayısı | K |
|---|---|
Tablo 3: toprak basıncı katsayısı, K (Mansur ve Avcı, 1970)
Zemin-kazık Sürtünme Açısı
Zemin ile kazık yüzeyi arasındaki sürtünme açısı, temel tasarımının önemli bir yönüdür.. Pratikte, birçok mühendis bu değere yaklaşık olarak şuna eşittir: 2/3 zeminin iç sürtünme açısının. ancak, Coyle ve Castello'nun çalışmasına dayanarak 1981, zemin-kazık sürtünme açısı yaklaşık olarak şuna eşittir: 80% zeminin iç sürtünme açısının. Diğer taraftan, NAVFAC DM7.2, zemin ile kazık arasındaki sürtünme açısını tahmin etmek için bu değerleri kullanır.:
| K = Efektif toprak basıncı katsayısı | NS |
|---|---|
Tablo 4: Zemin-kazık sürtünme açısı (NS) (Denklemin son teriminin sonuç değeri 7.2)
Kildeki kazıkların Sürtünme Direnci
Kil zeminlerdeki kazıkların sürtünme direncini hesaplamak, yeni değişkenlerin ortaya çıkması nedeniyle kumlu zeminlerdeki kadar zor olabilir., belirlemek o kadar da kolay olmayan. ancak, bu değişkenlerin değerlerini elde etmek için birkaç mevcut yöntem vardır..
λ Yöntemi
Vijayvergiya ve Focht'un çalışmasına dayanmaktadır. 1972, Kildeki kazıkların toplam sürtünme direnci, yığının ortalama birim sürtünme direnci belirlenerek tahmin edilebilir., Denklemler tarafından gösterildiği gibi 20 ve 21. λ değerleri kazığın penetrasyon derinliği arttıkça değişir. Tablo 5 kazığın gömme uzunluğu ile λ değişimini gösterir.
\( {f}_{ile ilgili} = \lambda \times [\bar{\sigma'}_{Ö} +( 2 \zamanlar {c}_{sen})] \) (20)
\({Q}_{s} = p \times L \times {f}_{ile ilgili} \) (21)
\( \bar{\sigma'}_{Ö} \): Tüm gömme uzunluğu için ortalama efektif dikey gerilim
csen: Ortalama drenajsız kesme dayanımı
| L (m) | λ |
|---|---|
Tablo 5: Kazık gömme uzunluğu ile λ değişimi (L)
α Yöntemi
α yöntemi, kazıkların birim sürtünme direncinin, zemin tabakasının drenajsız kohezyonunun ve buna karşılık gelen ampirik adezyon faktörünün ürününe eşdeğer olduğunu öne sürer. (a). Tablo 6 adezyon faktörünün drenajsız kohezyon ve atmosferik basınç oranına karşılık gelen değerini gösterir (csen/pa).
\(f = \alpha \times {c}_{sen}\) (22)
Bu nedenle, Bu yöntem kullanılarak kildeki kazığın toplam sürtünme direnci şu şekilde yeniden yazılabilir::
\({Q}_{s} = \sum (f \times p \times \Delta L) = \sum (\alpha \times {c}_{sen} \times p \times \Delta L)\) (23)
| csen/pa | a |
|---|---|
| 0.8 | |
pa K = Efektif toprak basıncı katsayısı 100 kN / m2
Tablo 6: α varyasyonu (Terzaghi, Gagalama, ve Mesri, 1996)
β Yöntemi
Yığın doygun kile çakıldığında, yığın etrafındaki boşluk suyu basıncı artar.. Bu method, etkili stres analizine dayalı, uzun vadeli için uygundur (süzülmüş) fazla boşluk suyu basıncının zaman içinde kademeli olarak dağılmasını dikkate aldığı için kazık yükü kapasitesinin analizleri. Tomlinson'a göre (1971), yumuşak killerde çakılan kazıklar, kazık yüzeyine yakın yeniden kalıplanmış zeminde yenilmelerin meydana geldiğini varsayar. Denkleme dayalı. 15, dönem (K × tanδ) kumdaki kazıkların birim sürtünme direnci için β ile temsil edilmelidir.. Zemin sürtünme açısı (NS) toprağın yeniden kalıplanmış süzülmüş sürtünme açısı ile değiştirilmelidir (Denklemin son teriminin sonuç değeri’R). Böylece, kildeki kazıkların birim sürtünme direncinin şuna eşit olduğu tahmin edilmektedir::
\(f = \beta \times {\sigma'}_{Ö}\) (24)
\(\beta = K \times tan {\Fi’}_{R}\) (25)
muhafazakar olarak, toprak basıncı katsayısı (K) dinlenme halindeki toprak basıncı katsayısına eşdeğerdir (K0) normal konsolide killer ve aşırı konsolide killer için değişir, aşağıdaki denklemlerde gösterildiği gibi:
\( Sonra denklemi kullanın {K}_{0} = 1 – olmadan {\Fi’}_{R}\) (Normal konsolide killer) (26)
\( Sonra denklemi kullanın {K}_{0} = (1 – olmadan {\Fi’}_{R}) \kez sqrt(önceki denklemlerde)\) (aşırı konsolide killer) (27)
önceki denklemlerde: aşırı konsolidasyon oranı
SkyCiv’in Temel Tasarım yazılımını denemek ister misiniz?? Ücretsiz aracımız, kullanıcıların herhangi bir indirme veya kurulum yapmadan yük taşıma hesaplamaları yapmasına olanak tanır!
Referanslar:
- İstinat duvarına etki eden yanal toprak basıncı, duvar toprak kütlesine itildiğinde pasif kabul edilir., Sonra denklemi kullanın. (2007). İstinat duvarına etki eden yanal toprak basıncı, duvar toprak kütlesine itildiğinde pasif kabul edilir. (7th Baskı). Sonra denklemi kullanın
- Sonra denklemi kullanın, R. (2016). Sonra denklemi kullanın (2nd Sürümü). Sonra denklemi kullanın.
- Sonra denklemi kullanın, Sonra denklemi kullanın. (2004). Sonra denklemi kullanın (4th Baskı). E & Sonra denklemi kullanın.


