çalıştırırken Tepki Spektrumu Analizi bir yapı üzerinde, İstenen sonuçları elde etmenin en önemli adımlarından biri, yer değiştirme için tek bir sonuç elde etmek için yazılım tarafından kullanılacak modal birleştirme yönteminin tanımlanmasıdır., reaksiyonlar, Iç kuvvetler, vb… her titreşim modu için elde edilen ham sonuçlardan her serbestlik derecesi için (modal cevaplar). Bu modal birleştirilmiş sonuçlar, yapıyı tasarlamak için kullanılanlardır., bu nedenle modal kombinasyon yöntemini doğru bir şekilde tanımlamak son derece önemlidir.. Bu makalede, Tepki Spektrum Analizi için bazı modal kombinasyon yöntemlerine değineceğiz..
Bir Tepki Spektrumu Analizi sırasındaki en önemli adımlardan birinin, her bir titreşim modu için doğal frekansın ve kütlesel katkısının değerlendirilmesi olduğunu belirtmek önemlidir., Dinamik Frekans Analizi ile ilgili belgelerimizi kontrol edin.
Yanıt Spektrumu Analizi için Modal Kombinasyon Yöntemleri
Modal kombinasyon için en bilinen ve kullanılan yöntemlerden bazıları şunlardır::
- ABS: Mutlak Toplam
- SRSS: Kareler Toplamının Karekökü
- CQC: Tam Kuadratik Kombinasyon
Genel olarak, toplam yanıtın tepe değerleri (\(r_o\)) yer değiştirmeler için, Iç kuvvetler, ve tepkiler ilgi çekicidir. Önceden belirtildiği üzere, tepe değeri, tepe modal yanıtların uygun şekilde birleştirilmesinden elde edilir. (\(r_{n, Ö}\))
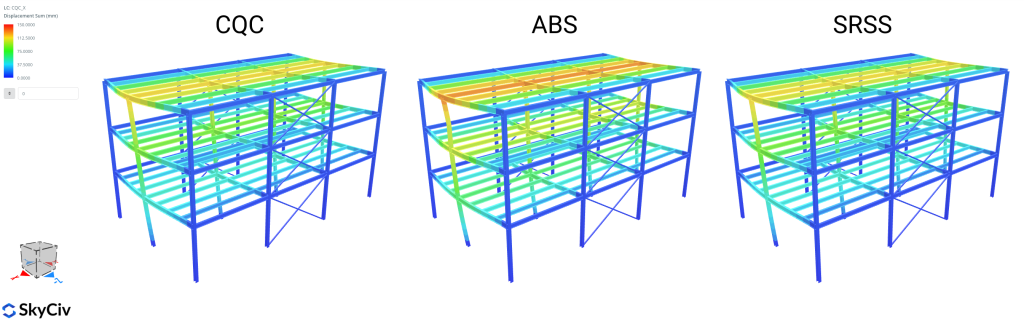
Mutlak Toplam (ABS)
Mutlak Toplam modal kombinasyon yöntemi, sonucun mutlak değerini alır. (yer değiştirme veya iç kuvvet) her titreşim modu için ve tüm bu mutlak değerleri özetler. fiziksel olarak, tüm tepe modal tepkilerin aynı anda meydana geldiğini varsayar. Bunu yaparak, en muhafazakar yöntemdir, her modal katkıyı olumlu hale getirdiği için, ve bu nedenle, yapısal tasarım uygulamalarında popüler değildir. Toplam yanıtın tepe değerini hesaplama formülü şöyledir::
\(r_o=\sum_{n=1}^{N} |r_{n,Ö}|\)
Nerede,
\(n\) bu \(n^{inci}\) analizde dikkate alınan titreşim modu
\(N) analizde dikkate alınan titreşim modlarının toplam sayısıdır
\(r_o\) en yüksek toplam yanıttır
\(r_{n,Ö}\) için en yüksek modal yanıttır. \(n^{inci}\) titreşim modu
Kareler Toplamının Karekökü (SRSS)
Kareler Toplamının Karekökü modal kombinasyon yöntemi, her bir titreşim modu için sonucun karelerinin toplamının karekökünü alır., toplam yanıtın zirvesine ilişkin bir tahmin sağlamak. Bu modal kombinasyon yöntemi, iyi ayrılmış doğal frekanslara sahip yapılar için mükemmel yanıt tahminleri sağlar., yapının doğal frekanslarının iyi ayrılmadığı durumlarda bu yöntem kullanılmamalıdır.. resmen, zirve toplam yanıtı aşağıdaki gibi ifade edilebilir:
\(r_o=\left(\toplam_{n=1}^{N} r^{2}_{n,Ö}\sağ)^{1/2}\)
Nerede,
\(n\) bu \(n^{inci}\) analizde dikkate alınan titreşim modu
\(N) analizde dikkate alınan titreşim modlarının toplam sayısıdır
\(r_o\) en yüksek toplam yanıttır
\(r_{n,Ö}\) için en yüksek modal yanıttır. \(n^{inci}\) titreşim modu
Tam Kuadratik Kombinasyon (CQC)
Tam Kuadratik Kombinasyon yöntemi, yakın aralıklı doğal frekanslara sahip bir yapıda modal yanıtları birleştirirken SRSS için belirtilen sınırlamanın üstesinden gelir.. Bu yöntemde, zirve toplam yanıtı, aşağıdaki formül uygulanarak elde edilir:
\(r_o=\left(\toplam_{ben=1}^{N}\toplam_{n=1}^{N} \Bükülme momentleri kesitlerde her yönde hesaplanır{içinde} \cdot r_{ben} \cdot r_{Hayır} \sağ)^{1/2}\)
Nerede,
\(n, \; i\) bu \(n^{inci}, \; ben ^{inci}\) analizde dikkate alınan titreşim modu
\(N) analizde dikkate alınan titreşim modlarının toplam sayısıdır
\(r_o\) en yüksek toplam yanıttır
\(r_{n,Ö}, \; r_{ben,Ö}\) için en yüksek modal yanıttır. \(n^{inci}, \; ben ^{inci}\) titreşim modu
\(\Bükülme momentleri kesitlerde her yönde hesaplanır{içinde}\) her toplama adımında birleştirilen iki mod için korelasyon katsayısıdır
Yukarıdaki formül, iki ayrı toplama grubu olarak yeniden yazılabilir., ilki, SRSS modal kombinasyon yöntemiyle aynıdır. İkinci çift toplam, tüm haçı içerir (\(i \neq n\)) şartlar, her biri olumlu ya da olumsuz olabilir, bu, CQC kullanılarak tepe toplam yanıt için yapılan tahminin, SRSS tarafından sağlanan tahminden daha büyük veya daha küçük olabileceği gerçeğini verir. :
\(r_o=\left( \toplam_{n=1}^{N} r^{2}_{n,Ö} + \korniş altı{\toplam_{ben=1}^{N}\toplam_{n=1}^{N}}_{i \neq n} \Bükülme momentleri kesitlerde her yönde hesaplanır{içinde} \cdot r_{ben} \cdot r_{Hayır} \sağ)^{1/2}\)
CQC denkleminde yalnızca bir terim tanımlanmamıştır: korelasyon katsayısı. Bu katsayı için en çok kullanılan denklemlerden biri:
\(\Bükülme momentleri kesitlerde her yönde hesaplanır{içinde} = frac{\xi^2(1+\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{içinde})^ 2}{(1-\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{içinde})^2+4\xi^2\beta_{içinde}}\)
Nerede,
\(\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{içinde}\) doğal frekansları arasındaki orandır \(ben ^{inci}\) ve \(n^{inci}\) modlar (\(\omega_i / \omega_n\))
\(\xi) yapı için sönüm katsayısıdır
Referanslar
Chopra, Bir. (2015, Haziran 4). Yapıların Dinamiği (4ed.). Pearson Yüksek Öğrenimi.
SkyCiv Yapısal 3D'de Yeni? Bugün ÜCRETSİZ kaydolun!
Ürün geliştirici
BEng (Sivil)



