Öğretici: Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür

Bu öğreticide, kafes yapınızı çözmek için Kesitler Yöntemini kullanmanın faydalarını keşfedecek ve öğreneceğiz. Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür? Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür, ziyaret edin Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür makale. Kesitler yöntemi, daha büyük kafes yapılarını hızlı bir şekilde çözmek için kullanılır., Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür. Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür’ Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür.

Harika olan şey, SkyCiv Kafes bunu sizin için otomatik olarak yapıyor. Kendi kafes kirişlerinizi modelleyin ve yazılım, bölüm yönteminin dışında adım adım etkileşimli çalışmayı gösterecektir.!

Video Eğitimini İzleyin

Örnek Soru

Çalıştığımız örnek için, aşağıdaki soruya bakacağız:

Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür: Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür, Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür 10, 11, ve 13 Kesit Yöntemi Kullanılarak Kafes Yapısı Nasıl Çözülür:

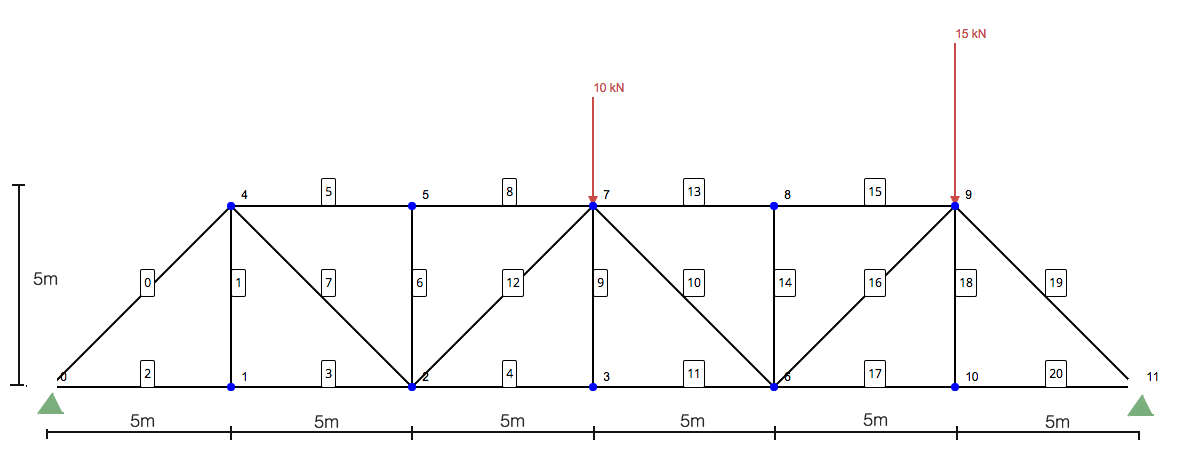
Adım 1: Desteklere Tepkileri Hesaplayın

Çoğu statik yapısal analiz gibi, önce onu bulup çözerek başlamalıyız. desteklerdeki reaksiyonlar. Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir.. Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir.:

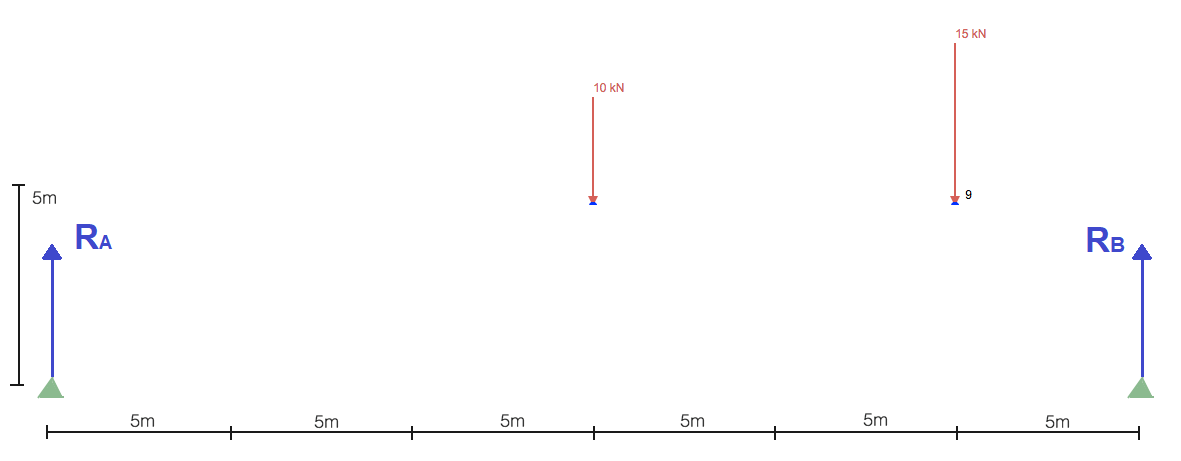
Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir., Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir.. Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir.:

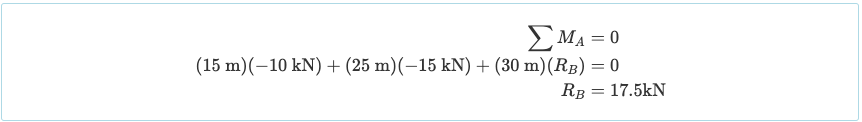
Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir. (R_B) dır-dir 17.5 yukarı yönde kN. Şimdi, Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir._Bir Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir.:

Adım 2: Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir.

Kesitler yöntemini kullanarak bir kafes kirişi çözmenin en önemli kısmı geliyor.. Bu bize kafes yapısını çözmede ilerlememiz gereken sınır koşullarını verecektir.. Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.. Yani, Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.:

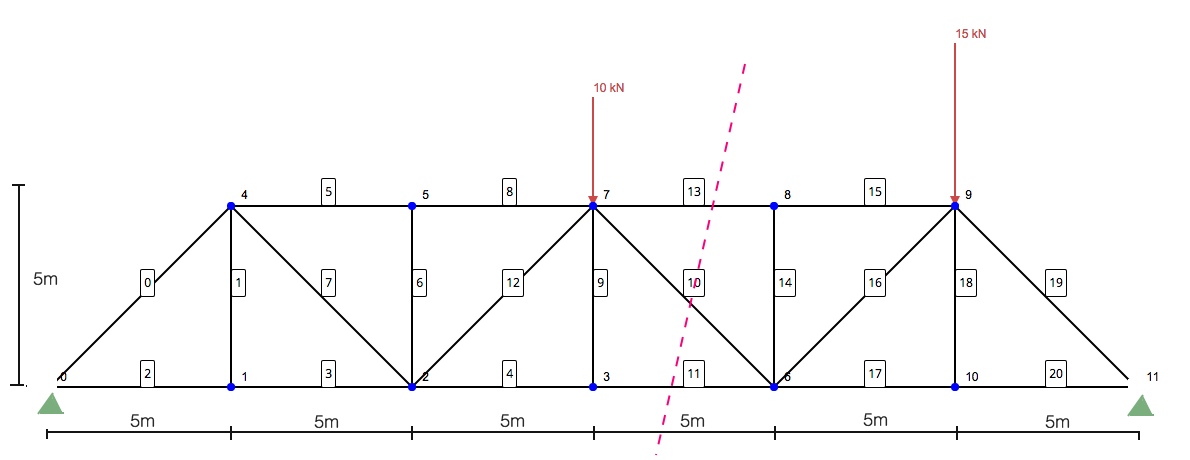
Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır., Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.:

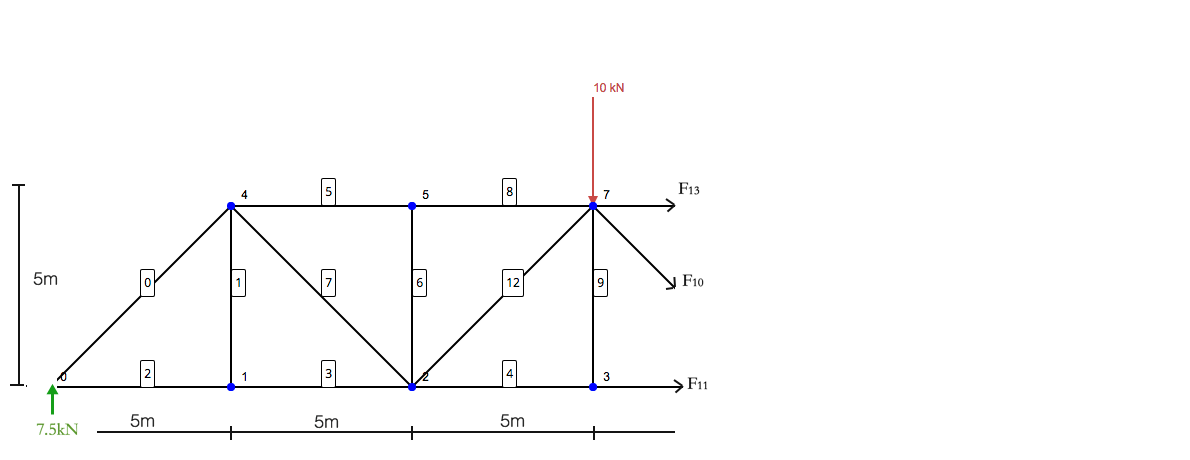
Şimdi bu yapıyı tek ayakta duran bir yapı olarak düşünün.. Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır. – Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.. Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır. (F₁₃, F₁₀, F₁₁) Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.. Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır. 7 – Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır. 13 ve 10 – Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.₁₁ Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır..

Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır., Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.:

Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.:

[matematik]
\başla{hizalamak}
+\yukarı ok metin{ } \toplam{F_y} &= 0\\
7.5\Metin{ kN} – 10 \Metin{ kN} – F_{10}olmadan(45^{\daire}) &= 0\\
F_{10} &= -3.536 \Metin{ kN}
\son{hizalamak}
[matematik]

Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır. 7:

[matematik]
\başla{hizalamak}
+\daireokleft metin{ } \toplam{M_7} &= 0\\
-(15 \Metin{ m})(7.5 \Metin{ kN}) + (5 \Metin{ m})F_{11} &= 0\\
F_{11} &= 22.5 \Metin{ kN}
\son{hizalamak}
[matematik]

Bu yapısal analiz yöntemi, tüm yapıyı birleştirme yöntemini kullanarak çözmek zorunda kalmadan bazı elemanları çözmeye çalışırken son derece yararlıdır.:

[matematik]
\başla{hizalamak}
+\sağ ok metin{ } \toplam{F_x} &= 0\\
F_{13} + F_{11} + F_{10}çünkü(45^{\daire}) &= 0\\
F_{13} &= -F_{11} – F_{10}çünkü(45^{\daire}) \\
F_{13} &= – (22.5 \Metin{ kN}) – (-3.536 \Metin{ kN})çünkü(45^{\daire}) \\
F_{13} &= -22.5 \Metin{ kN} + (3.536 \Metin{ kN})çünkü(45^{\daire}) \\
F_{13} &= -20 \Metin{ kN}
\son{hizalamak}
[matematik]

Son çözüm

Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz.. Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz.. Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz., Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz. (Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz. Kafes Hesaplayıcı) Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz.!

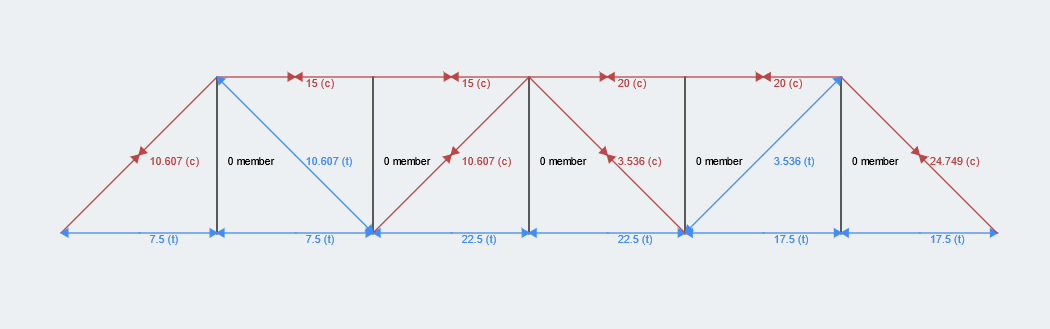
Adımların Özeti

• Her zaman desteklerdeki reaksiyonları hesaplayarak başlayın
• Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz.
• Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz.
• Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz. 0
• Bu sonuçları truss yapısında kalan üyeleri çözmek için kullanabiliriz.

SkyCiv Truss Yazılımı

Bu öğreticiyi projeleriniz için yararlı bulduğunuzu umuyoruz.. Ziyaret edin kafes öğreticiler truss hakkında daha faydalı bilgiler için ve Eklem Yöntemi ile kiriş çözme kılavuzu.

SkyCiv Kafes bölümlerin yöntemini sizin için otomatik olarak hesaplayabilir. Veya bizim deneyin Ücretsiz Kafes Hesaplayıcı sana son cevabı verecek olan (elle hesaplama yok).

SkyCiv yazılımının daha fazla işlevselliğini keşfetmek için, başlamak için bugün kaydolun!

Ücretsiz Başlayın