ACI'ye uygun tek kazık tasarımı 318 (2014)

Kazıklar, yükleri üst yapıdan daha derindeki zemine veya yeterli taşıma kapasitesine sahip bir kayaya aktaran uzun ve narin elemanlardır.. Yığınlar için kullanılan malzemeler ahşap içerebilir, çelik, ve beton. Yığının zemine montajı sürülebilir, delinmiş, veya daha sonra kazık başlıklarına bağlanan kriko. birçok faktör, site koşulları gibi, toprak tipi, yüklerin iletimi, kazıkların tipini ve kurulumunu sınıflandırmak için kabul edilir. Bu makale, Amerikan Beton Enstitüsü'ne göre bir beton kazık tasarlamaya odaklanacaktır. (ACI) 318 – 2014.

SkyCiv Foundation Design modülü, Amerikan Beton Enstitüsü'ne uygun kazıkların tasarımını içerir. (ACI 318) ve Avustralya Standartları (GİBİ 2159 & 3600).

SkyCiv’in Temel Tasarım yazılımını denemek ister misiniz?? Ücretsiz aracımız, kullanıcıların herhangi bir indirme veya kurulum yapmadan yük taşıma hesaplamaları yapmasına olanak tanır!

Temel Tasarım Hesaplayıcı

Bir yığının yük taşıma kapasitesi

Genel olarak, kazıklara uygulanan düşey yükler, kazık uç yatağı tarafından taşınır., ve uzunluğu boyunca gelişen cilt sürtünme direnci. Nihai yük taşıma kapasitesi (Q_U) denklem ile temsil edilecektir (1). İzin verilen yük taşıma kapasitesini hesaplamak için bir güvenlik faktörü uygulanır (Q_Bir).

\({Q}_{sen} = {Q}_{p} + {Q}_{s}\) (1)

Q_U = Nihai yük taşıma kapasitesi

Q_P = Uç Dayanma Direnci

Q_S = Ciltte Sürtünme Direnci

\({Q}_{Bir} = frac{{Q}_{U}}{FOS} \) (2)

Q_Bir = İzin verilen yük taşıma kapasitesi

FOS = Güvenlik faktörü

Daha ayrıntılı bir kılavuz için, hesaplama ile ilgili makalemize göz atın cilt sürtünme direnci ve uç taşıma kapasitesi.

Tek bir yığının yapısal gücü

Kazıklar ayrıca eksenel kuvvetlere maruz kalır, kesme kuvveti, ve eğilme momenti, bu yüzden yapısal olarak sütunlara benzer şekilde tasarlanmıştır.. Bölüm 10.5.1.1 tüm faktörlü yükün karşılık gelen tasarım gücünü aşmaması gerektiğini belirtir.

\( {øP}_{N} ≤ {P}_{U} \) (3a)

\( {Ağrı}_{N} ≤ {M}_{U} \) (3b)

\( {øV}_{N} ≤ {V }_{U} \) (3c)

P_U, M_U, V _U = Faktörlü eksenel, bükülme anı, kesme yükleri

P_N, M_N, V _N = Nominal eksen, bükülme anı, kesme yükleri

ø = Mukavemet azaltma faktörleri (Tablo 1)

Mukavemet Azaltma Faktörleri(ϕ)
Eksenel	0.65-0.90
Eğilme	0.65-0.90
Kesme	0.75

Tablo 1: Mukavemet Azaltma Faktörleri (Tablo 21.2.1, ACI 318-14)

Tek kazık kesme kapasitesi (øV_N)

Nominal kesme mukavemeti, beton ve çelik donatının kesme kapasitelerinin birleşik katkılarına eşdeğer olacaktır..

Betonun kesme dayanımı (V _c)

Betonun kesme kapasitesine katkısı denklemde gösterildiği gibi hesaplanır. (4) bölümünde tanımlanan 22.5.5.1 ACI 318-14.

\( {V }_{c} = 0.17 × λ × sqrt{fc'} × b × d \) (4)

λ = Somut modifikasyon faktörü = 1 (Normal ağırlıklı beton, Tablo 19.2.4.2)

fc’ = Betonun Mukavemeti

b = Kazık genişliği veya çapı

d = 0.80 × yığın derinliği (Bölüm 22.5.2.2)

Çelik çubukların kesme mukavemeti (V _s)

Yanal kesme takviyesinin kesme kapasitesine katkısı, denklemler arasındaki minimum olarak hesaplanır. (5) ve (6).

\( {V }_{s} = 0.066 × sqrt{fc'} × b × d \) (5)

\( {V }_{s} = frac{{Bir}_{v} × {f}_{YT} × gün }{s} \) (6)

Bir_V = Kesme donatı çubuklarının alanı

f_YT = Kesme donatı çubuklarının akma dayanımı

s = Kesme donatı çubuklarının merkezden merkeze aralığı

Nominal kesme mukavemeti (øV_N)

Denklemin çıktısını özetlemek 4-6 kazık nominal kesme mukavemeti ile sonuçlanacaktır. Mukavemet azaltma faktörü (Ö) eşit olacaktır 0.75 Tabloda tanımlandığı gibi 22.2.1 ACI 318-14.

\( {øV}_{N} = ø × ({V }_{c} + {V }_{s}) ≤ {øV}_{U} \) (7)

Temel Tasarım Hesaplayıcı

Tek bir yığının eksenel ve eğilme kapasiteleri (øP_N, Ağrı_N )

Eksenel ve eğilme kapasiteleri bir etkileşim diyagramı kullanılarak kontrol edilir. Bu diyagram, saf eğilme noktasından dengeli bir noktaya ulaşılana kadar yükteki bir artışın neden olduğu eğilme ve eksenel kapasitelerin davranışının görsel bir temsilidir..

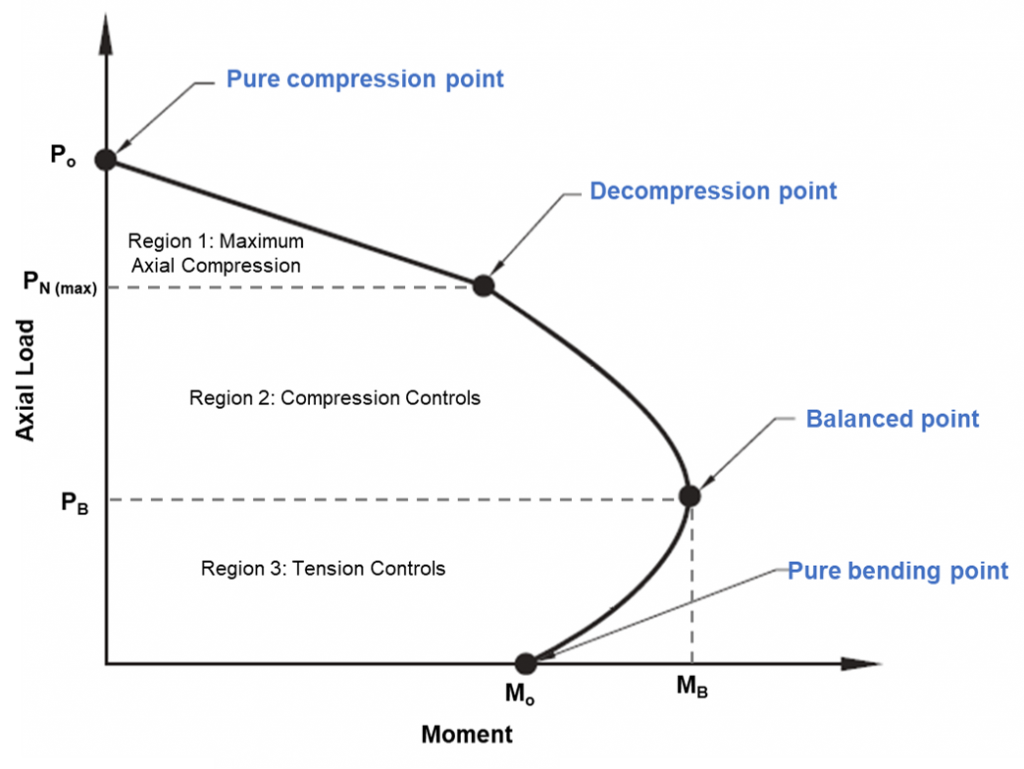
Figür 1: Sütun Etkileşim Şeması

Sütun etkileşim diyagramı

Diyagramdaki saf sıkıştırma noktası, yığının tamamen sıkıştırmada başarısız olacağı yerdir.. Bu noktada, eksenel yük, bükülmeden sıkıştırmada kalmak için bölümün plastik merkezine uygulanır. Saf sıkıştırma noktası arasındaki dekompresyon noktalarına kadar olan yığının mukavemeti lineer enterpolasyon ile hesaplanabilir. Dekompresyon noktası, aşırı sıkıştırıcı fiberdeki beton şekil değiştirmesinin eşit olduğu yerdir. 0.003, ve aşırı gerilimli fiberdeki gerilme sıfırdır. Saf bükülme noktası, eksenel yük kapasitesinin sıfır olduğu yerdir.. Dekompresyon noktasından saf bükülme noktasına geçiş arasında, dengeli bir durum elde edilir. Bu noktada, beton şekil değiştirme sınırında (e_c=0,003), ve dış çelik gerinim verime ulaşır (e_s=0.0025). Diyagramın dışında herhangi bir eksenel yük ve eğilme momenti kombinasyonu arızaya neden olacaktır..

Tasarım için maksimum nominal eksenel basınç dayanımı (øP_N)

Bir bölümün tasarım eksenel mukavemeti yalnızca aşağıdakilerle sınırlı olacaktır: 80-85% tesadüfi eksantrikliği hesaba katan nominal eksenel mukavemetin.

\( {øP}_{N} = ø × {P}_{Ö} \) (8a)

\( {P}_{Ö} = F × [0.85 × {f}_{c} × ({Bir}_{g} – {Bir}_{Aziz}) + ({f}_{Y} × {Bir}_{Aziz}) ] \) (8b)

F = 0.80 (Kravatlar)

F = 0.85 (Sarmal)

Bir_G = Kazık kesitinin brüt alanı

Bir_Aziz = Boyuna çelik çubukların toplam alanı

f_Y = Çelik çubukların akma dayanımı

Nominal eğilme mukavemeti (Ağrı_N)

Sütun için etkileşim diyagramının oluşturulması, bir dizi P değerinin çizilmesini içerir._N ve M_N. P için değerler_N çekme ve basma kuvvetlerinin toplamına eşit olacaktır., Şekil 2a ve 2b'de gösterildiği gibi, karşılık gelen M iken_N nötr eksen etrafındaki bu kuvvetleri çözerek hesaplanır. Bu kuvvetler, sıkıştırma alanına etki eden sıkıştırma kuvvetini ve takviye çubuklarının her biri tarafından uygulanan, sıkıştırma veya çekme olabilen kuvvetleri içerir.. Aşağıda sunulan denklemleri kullanarak bir etkileşim diyagramı oluşturmak için genel bir prosedür önerilmektedir..

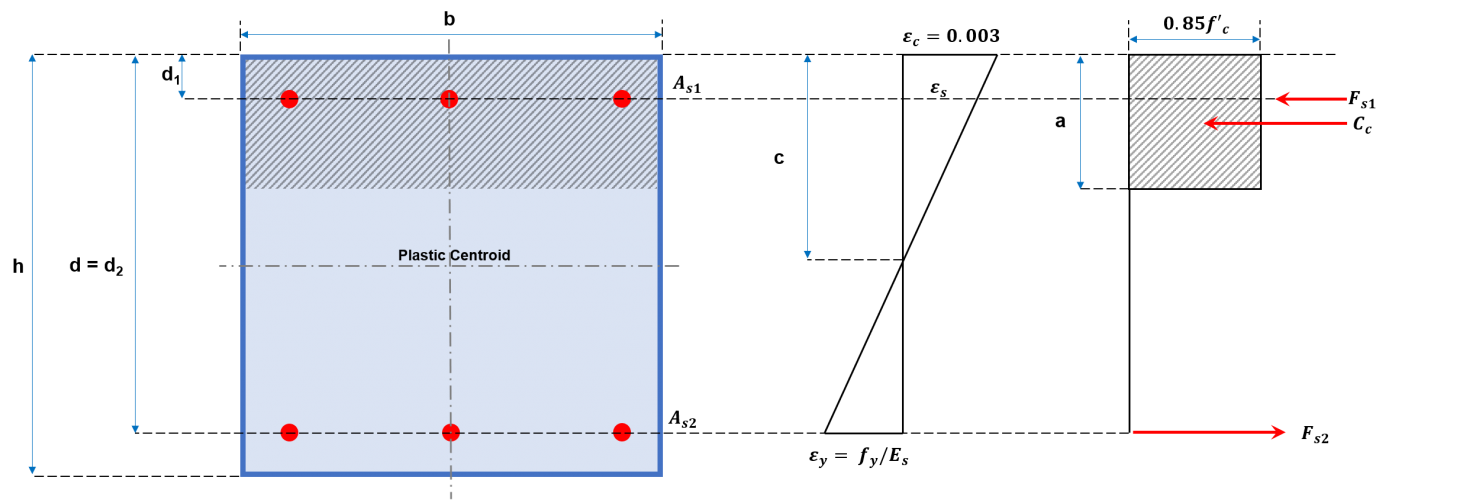
Şekil 2a: Dikdörtgen kolon kesiti

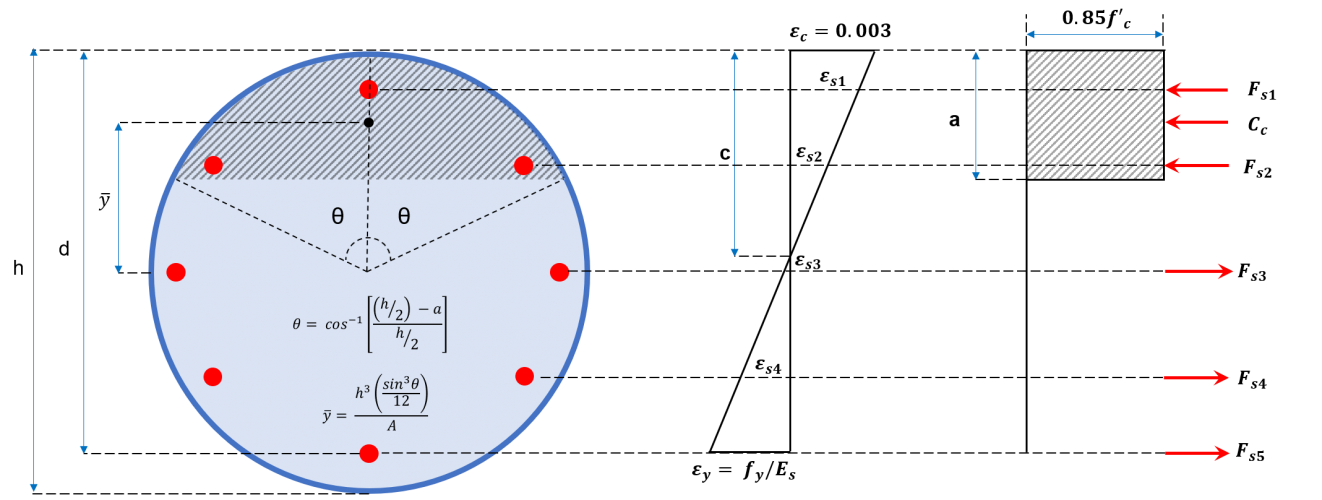
Şekil 2b: Dairesel kolon kesiti

Bir sütunun etkileşim diyagramı için genel prosedür

(1) P değeri için hesaplayın_Ö ve P_N (denklemler 8a ve 8b).

(2) c ve donatılardaki gerinimleri belirleyin.

\( c = 0.003 × frak{{d}_{1}}{0.003 + (İLE + {e}_{Y})} \) (9)

c = Nötr eksen derinliği

e_Y = Çeliğin gerinim = f_Y/E_s

Z = Keyfi değer (0, -0.5, -1.0, -2.5)

Tarafsız eksenin çeşitli konumları seçilerek bir dizi durum dikkate alınacaktır., c. Tarafsız eksenin konumlarını ayarlamak için, çeliğin akma dayanımına keyfi bir Z değeri çarpılarak farklı çelik gerinimleri seçilecektir.. Z için geniş bir değer aralığı vardır.. ancak, etkileşim diyagramı için kullanılacak yalnızca dört zorunlu nokta vardır.

• Z = 0: Bu noktada, gerilimdeki aşırı tabakadaki gerinim sıfırdır. Bu nokta, tüm boyuna çubuklarda izin verilen sıkıştırmalı bindirmeli eklemeden bir germe bindirmeli eklemeye geçişi gösterir..
• Z = -0.5: bu gerinim dağılımı, bir kolondaki germe bindirme ekinin uzunluğunu etkiler & geleneksel olarak bir etkileşim diyagramında çizilir.
• Z = -1: bu dengeli bir koşulun noktasını işaretler. Bu gerinim dağılımı, kesitin basma yüzeyinin ezilmesinden kaynaklanan basma kırılmalarından boyuna donatının akması ile başlatılan çekme kırılmalarına kadar olan değişimi gösterir..
• Z = -2.5: bu nokta, gerilim kontrollü gerinim sınırına karşılık gelir. 0.005.

(3) Takviye katmanlarındaki gerilmeleri hesaplayın.

\({f}_{ve} ={e}_{ve} × {E}_{s} \) (10)

f_ve = Çelikte gerilme

e_ve = Çelikteki gerinim

\({e}_{ve} = frac{c -{d}_{ben}}{c} × 0.003 \) (11)

E_s = Çeliğin elastisite modülü

(4) Sıkıştırma stres bloğunun yüksekliğini belirleyin, a.

\(a = {b}_{1} × c \) (bir ≤ h)(12)

f'c ≤ için 4000 psi (28 MPa):

b₁ = 0.85

f'c için > 4000 psi (28 MPa):

\( {b}_{1} = 0.85 – \çatlamak{0.05 × (f'c – 4000)}{1000} \) (İmparatorluk)

\( {b}_{1} = 0.85 – \çatlamak{0.05 ×(f'c – 28)}{7} \) (Metrik)

(5) Beton ve çelikteki kuvvetleri hesaplayın.

Basınç gerilimi bloğunun alanı:

\({Bir}_{c} = bir × b \) (Dikdörtgen kesit)

\({Bir}_{c} ={h}^{2} × frak{θ – günahθ çünküθ}{4} \) (Dairesel kesit alanı)

Betonda basınç kuvveti:

\({C}_{c} = (0.85 × f'c) × {Bir}_{c}\) (14)

Çelikte çekme kuvveti (d_ben≤ bir):

\({F}_{ve} = {f}_{ve} × {Bir}_{ve} \) (15)

Çelikte basınç kuvveti (d_ben > a):

\({F}_{ve} = [{f}_{ve} – (0.85 × f'c)] × {Bir}_{ve} \) (16)

(6) Eksenel kapasite için hesaplayın (P_N).

\({P}_{N} = {C}_{c} + Σ {F}_{ve} \) (17)

(7) Eğilme kapasitesi için hesaplayın (M_N).

\({M}_{N} = [{C}_{c} × (\çatlamak{h}{2} – \çatlamak{a}{2})]+ Σ [{F}_{ve} × (\çatlamak{h}{2} – {d}_{ben}) \) (18)

(8) Mukavemet azaltma faktörünün değerini hesaplayın (Ö).

Tabloda gösterildiği gibi 1, hem eksenel hem de eğilme için mukavemet azaltma faktörü, 0.60 -e 0.90. Bölüm 21.2 ACI 318-14 şu an için değerini gösteriyor, eksensel kuvvet, veya birleşik moment ve eksenel kuvvet, Tabloda gösterildiği gibi 2 altında.

sınıflandırma	Sarmal	bağlı
Sıkıştırma kontrollü	0.75	0.65
Sıkıştırmadan gerilime geçiş	0.75 + [50 × (et – 0.003) ]	0.65 + [(250/3) × (et – 0.003) ]
Gerilim kontrollü	0.90	0.90

Tablo 2: Eksenel için Mukavemet Azaltma Faktörleri, moment veya eksen ve momenti birleştirin (Tablo 21.2.2, ACI 318-14)

(9) Adımları tekrarlayın 2-8 Z için çeşitli değerlerle.

(10) øP değerlerini diyagrama çizin_N ve øM_N.

SkyCiv Ücretsiz Temel Hesaplayıcı ile Beton Kazık Tasarımı

SkyCiv Ücretsiz Temel Hesaplayıcı beton kazık tasarımı ve temel ve beton kazık tasarımı gibi diğer görevlerde size yardımcı olur. Hesaplayıcımızın beton kazık projenizde size nasıl yardımcı olabileceğini keşfetmek için şimdi göz atın!

Temel Tasarım Hesaplayıcı

Referanslar

• • Yapısal Beton için Bina Kodu Gereklilikleri (2014). AC! 318-14 Amerikan Beton Enstitüsü.
  • Hsiao, JK. (2012). Yük Momentinde Eğilme Ekseni Etkileri (öğleden sonra) Sınırlı Sayıda Boyuna Donatı Çubuğu Kullanan Dairesel Beton Kolonlar için Etkileşim Diyagramları. Elektronik Yapı Mühendisliği Dergisi 12 (1). http'den alındı://www.ejse.org