Çelik bağlantı tasarımında, cıvatalar genellikle belirli bir yüke direnmek için tek bir gövde gibi hareket edecek bir cıvata grubu olarak tasarlanırlar.. Bir cıvata grubunun gücü, genellikle en kritik cıvatasının kontrol gücü ile hesaplanır.. Doğrudan yükler, toplam cıvata sayısı arasında dağıtılır, yüklerin eksantrikliğinden kaynaklanan indüklenen moment, cıvata grubunun atalet momentine ve ağırlık merkezinden uzaklığına göre dağıtılır.. Bu analiz elastik analiz olarak adlandırılır.. Yük dağılımına ilişkin basitleştirilmiş ve muhafazakar varsayımları nedeniyle, genellikle aşırı tasarlanmış cıvatalı bağlantılar verir.
Değer mühendisliği ve ekonomik tasarımlardan bahsederken, çoğu üretici tarafından esnek olmayan yaklaşım tercih edilir. Aynı büyüklükteki yükler için daha az sayıda cıvata gerektirir. Esnek olmayan yaklaşımı yapmak için, anlık dönüş merkezi (ICOR) yinelemeleri kullanan yöntem en iyi yoldur.
Bu makalede, gücünün nasıl hesaplanacağını göstereceğiz. civatalı bağlantı ICOR yöntemini kullanarak. Cıvata başına reaksiyonlar Denklem kullanılarak hesaplanacaktır. (7-1) sayfalarda 7-7 of AISC 15. Baskı Kılavuzu. Bu daha sonra cıvata grubunun anlık merkezinin varsayılan konumunun doğru olup olmadığını kontrol etmek için kullanılacaktır.. En sonunda, doğru IC konumuna sahip olduğumuzda, daha sonra gücünü belirlemek için cıvata grubu katsayısı C'yi hesaplayacağız.
Cıvata grubu katsayısının elde edilmesinde ICOR yönteminin kullanılması, Ani Merkezin elde edilmesi için deneme yanılma yöntemini gerektirdiğinden uzun bir süreçtir. (IC) yer. Şu günlerde, bilgisayar çözücülerin kullanımı ile, bir cıvata grubunun IC'si programlanmış yinelemeler kullanılarak kolayca hesaplanabilir. SkyCiv Cıvata Grubu Çözücü IC konumunu ve cıvata grubu katsayısını saniyeler içinde belirlemek için hızlı bir yineleme yöntemi kullanır. Şu anda AS'de uygulanmaktadır. 4100 tasarım kodu, ancak yakında tasarım kodlarının geri kalanına entegre edilecek.
Cıvata Grubu Özelliklerini Alma
Eksantrik dikey kesme yükü ile yüklenmiş dört cıvatadan oluşan bir cıvata grubu üzerinde basit analizimize başlayalım. 10 kips . x ekseni boyunca yükün eksantrikliği 4 Cıvata grubunun sağında inç. Dikeyden açı sıfırdır ve y ekseni boyunca eksantriklik sıfırdır.
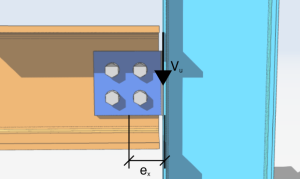
\(V_{sen} = 10 kip \)
\(\teta = 0 derece)
\(e_{x} = 4 içinde)
\(e_{Y} = 0in)
İlk yapmamız gereken cıvata grubumuzdaki tüm cıvataların koordinatlarını almaktır.. Görsel kılavuzların ve tabloların kullanılması şiddetle tavsiye edilir..
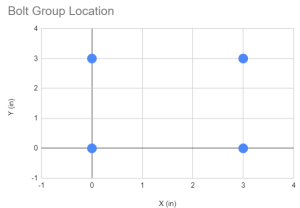
| Mağaza kimliği | X (içinde) | Y (içinde) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
x boyunca cıvata grubunun ağırlık merkezini almak için- ve y eksenleri, aşağıdaki formüle ihtiyacımız var.
İzin Vermek \(n \) = toplam cıvata sayısı
\(X_{bilgisayar bilimi} = frac{\toplam X}{n}\)
\(Y_{bilgisayar bilimi} = frac{\toplam Y}{n} \)
Sonra, bizim çözümümüz:
\(X_{bilgisayar bilimi} = frac{\toplam X}{n} = frac{0 içinde + 0 içinde + 3 içinde + 3 içinde}{4} = 1.5 içinde)
\(Y_{bilgisayar bilimi} = frac{\toplam Y}{n} = frac{0 içinde + 3 içinde + 0 içinde + 3 içinde}{4} = 1.5 içinde)
IC'nin yerini varsayın.
merkezini aldıktan sonra, anlık merkezin yerini alacağız \(IC). İlk deneme olarak, IC'nin cıvata grubunun geometrik merkezinde yer aldığını varsayabiliriz..
Yani, farz etmek
\(X_{IC} = X_{bilgisayar bilimi} = 1.5 içinde)
\(Y_{IC} = Y_{bilgisayar bilimi} = 1.5 içinde)
Sonra, her cıvatanın yer değiştirmesini IC'nin konumuna göre tablo haline getiriyoruz. Bunu, önce x boyunca olan mesafeyi ve y boyunca olan mesafeyi alarak basitçe yapabiliriz., sonra yer değiştirmesini al
| Mağaza kimliği | cx (içinde) | cy (içinde) | c (içinde) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
Nerede,
\(c_{x} = X_{ben} – X_{IC}\)
\(c_{Y} = Y_{ben} – Y_{IC}\)
\(c = sqrt{{\ayrıldı(c_{x} \sağ)}^{2} + {\ayrıldı(c_{Y} \sağ)}^{2}}\)
Cıvata Hayır için. 1, bizim çözümümüz
\(c_{x} = 0in – 1.5 içinde = -1.5 içinde)
\(c_{Y} = 0in – 1.5 içinde = -1.5 içinde)
\(c = sqrt{{\ayrıldı( -1.5 sağda)}^{2} + {\ayrıldı( -1.5 sağda)}^{2}} = 2.121in\)
IC'den cıvata wrt mesafesi başına deformasyonu hesaplayın
Dolayısıyla, varsayılan IC konumundan cıvata mesafelerini aldıktan sonra, daha sonra her bir cıvatanın deformasyonunu mesafesinin bir fonksiyonu olarak hesaplarız.
Cıvata başına maksimum deformasyon, ayarlanır \(\Delta_{max} = 0.34 içinde), AISC sayfasında açıklandığı gibi bir ASTM cıvatası için deneysel verilere dayanmaktadır 7-8. Doğrusal orantı kullanarak, ve ayar \(\Delta_{max} = 0.34 içinde), tek bir cıvatanın maksimum mesafeye olan kısmına göre deformasyonunu hesaplayabiliriz \(c_{max}\). elde etmek için denklem = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu.
\(\Delta_{1} = 0,34in time sol( \çatlamak{c}{c_{max}}\sağ) \)
Cıvata Hayır için. 1, deformasyon
\(\Delta_{1} = 0,34in time sol( \çatlamak{2.121 içinde}{2.121 içinde}\sağ)\)
Cıvataların geri kalanı için, hesaplanan deformasyonlar aşağıda tablolanmıştır.
| Mağaza kimliği | \(\Delta\) (içinde) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Cıvata başına reaksiyonları alın
Cıvata başına deformasyona sahip olduğumuzda, AISC 15th Ed'i kullanabiliriz. Eşitlik (7-1) cıvata başına reaksiyonları almak için.
\(R = R_{ulti} \ayrıldı ( 1 – e^{-10\Delta}\sağ )^{0.55}\)
NS \(R_{ulti}\) denklemde bir cıvata üzerindeki varsayılan nihai yük, cıvata kesme kuvveti olarak ayarlayabileceğimiz.
\(R_{ulti} = phi R_{n} \)
Örneğimiz için, cıvata kesme mukavemetini kullanacağız \(24.4 kip). Cıvata grubu katsayısını hesapladığımızda bu sadece iptal edeceği için başka bir değer kullanılmasına da izin verilir. \(C) daha sonra.
Cıvata Hayır için. 1, hesaplanan reaksiyon
\(R = R_{ulti} \ayrıldı ( 1 – e^{-10\Delta}\sağ )^{0.55}\)
\(R = 24.4 kip sol ( 1 – e^{-10 \kez kaldı ( 0.34 sağda )}\sağ )^{0.55}\)
\(R = 23.949 kip)
Cıvataların geri kalanı için, hesaplanan reaksiyonlar aşağıdaki gibidir. Aynı zamanda, cıvata reaksiyonunun bileşenleri \(R) x ve y boyunca da gösterilir.
| Mağaza kimliği | R (kip) | Rx (kip) | Ry (kip) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
Cıvata No.1 için, x ve y bileşenlerini elde etmek için çözümler aşağıda gösterilmiştir..
\(R_{x} = -R sol ( \çatlamak{c_{Y}}{c} \sağ ) = -23.949 \kez kaldı ( \çatlamak{-1.5içinde}{2.121içinde} \sağ ) = 23.949 kip)
\(R_{Y} = R sol ( \çatlamak{c_{x}}{c} \sağ ) = 23.949 \kez kaldı ( \çatlamak{1.5içinde}{2.121içinde} \sağ ) = 23.949 kip)
Dahası, eksantriklik nedeniyle cıvata başına indüklenen moment yükünü almalıyız. Bunu hesaplamak için, bileşenleri kullanıyoruz \(R_{x}\) ve \(R_{Y}\) ve onları eksantrikliklerle çarpın \(c_{Y}\) ve \(c_{x}\), sırasıyla.
Cıvata No.1 için, IC'ye verilen anlık tepki
\(M_{r} = -R_{x}c_{Y} + -R_{Y}c_{x} \)
\(M_{r} = -16.937 kip kez sol ( -1.5sağda) + -16.937 kip kez sol ( -1.5 sağda ) \)
\(M_{r} = 50.811 tavuk-in)
Cıvataların geri kalanı için, karşılık gelen moment reaksiyonları aşağıda tablolaştırılmıştır.
| Mağaza kimliği | Bay (tavuklu) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀Bay = 101.622 |
IC konumunu doğrulama
Artık cıvata başına kesme ve moment reaksiyonlarına sahip olduğumuza göre, bunu, bu cıvata grubunun dayandığı Pu yükünün miktarını belirlemek için kullanacağız.. Bunu yapmak için, x boyunca tüm reaksiyonların toplamının ve y boyunca tüm reaksiyonların toplamının sonucunu alacağız..
Bir önceki bölümden, biz bunu hesapladık
\(\toplam R_{x}=0kip\)
ve
\(\toplam R_{Y}=0kip\)
Yani,
\(P_{sen} = sqrt{{\ayrıldı( \toplam R_{x} \sağ)}^{2} + {\ayrıldı( \toplam R_{Y} \sağ)}^{2}} = 0 kip)
Ortaya çıkan yük nedeniyle \(P_{sen} = 0kip), bu noktada verilerimiz sıfır olacağından doğrulamaya devam etmemeye karar verebiliriz.. Ayrıca I.C.'nin ilk varsayılan konumunun da olduğunu çıkarabiliriz., cıvata grubunun merkezinde olan, yanlış. ancak, bu tartışmanın amacı için, aşağıdaki adımlarla devam edeceğiz.
\(P_{ux} = -P_{sen}günahsol ( \teta sağ ) = 0 kip \)
\(P_{uy} = -P_{sen}çünküsol ( \teta sağ ) = 0 kip \)
\(M_{sen} = -P_{ux}\ayrıldı ( Y_{bilgisayar bilimi} + e_{Y} – Y_{IC} \sağ ) + -P_{uy} \ayrıldı (X_{bilgisayar bilimi} + e_{x} – X_{IC} \sağ ) = 0 kip \)
Dan beri,
\(P_{ux} \neq toplam R_{x} \)
\(P_{uy} \neq toplam R_{Y} \)
\(M_{sen} \ben M_ değilim{r} \)
Bu nedenle, I.C'nin varsayılan konumu. yanlış. Artık bir sonraki varsayılan konumla devam edebiliriz.
SkyCiv, cıvata grubu hesaplamasının Avustralya Standart Modülüne tam entegrasyonuna sahiptir. Bağlantı tasarımı yazılımımızı denemek ister misiniz??
İkinci Yineleme
İkinci tekrarımız için, I.C olduğunu varsayalım.. aşağıda gösterilen koordinatlarda bulunur.
Farz etmek
\(X_{IC} = 0.062 içinde)
\(Y_{IC} = 1.5 içinde)
Sonra, ilk yinelememizde yaptığımız adımları yapalım. Özetle, aşağıdaki tablo koordinatları gösterecektir, her cıvatanın varsayılan I.C'den uzaklığı, ve mesafeye göre ilgili deformasyon.
| Mağaza kimliği | X (içinde) | Y (içinde) | cx (içinde) | cy (içinde) | c (içinde) | \(\Delta\) (içinde) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Hesaplanan ağırlık merkezinin cıvata grubu Cıvata koordinatlarında hiçbir şey değişmediğinden hala aynı.
\(X_{bilgisayar bilimi} = 1.5 içinde)
\(Y_{bilgisayar bilimi} = 1.5 içinde)
Sonra, x boyunca reaksiyonları hesaplıyoruz, y boyunca reaksiyonlar, ve karşılık gelen an. Değerler aşağıda tablolaştırılmıştır.
| Mağaza kimliği | R (kip) | Rx (kip) | Ry (kip) | Bay (tavuklu) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀Bay = 222 |
Sonraki, x ve y boyunca tüm reaksiyonların sonuçtaki yükünü belirleriz.
\(P_{sen} = sqrt{{\ayrıldı( \toplam R_{x} \sağ)}^{2} + {\ayrıldı( \toplam R_{Y} \sağ)}^{2}}\)
\(P_{sen} = sqrt{{\ayrıldı( 0 kipsağ)}^{2} + {\ayrıldı( 40.703 kipsağ)}^{2}}\)
\(P_{sen} = 40.703 kip)
Sonra, verilen yükün bileşenleri \(\teta) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu.
\(P_{ux} = -P_{sen}günah sol ( \teta sağ ) = -41kip times sin left ( 0 derece sağ )= 0 kip)
\(P_{uy} = -P_{sen}çünkü sol ( \teta sağ ) = -41kip times çünkü sol ( 0 derece sağ )= -41 kip)
Daha sonra, varsayılan I.C ile ilgili moment yükünü çözmek için bu bileşenleri kullanacağız..
\(M_{sen} = -P_{ux} \ayrıldı ( Y_{bilgisayar bilimi} + e_{Y} – Y_{IC} \sağ) + P_{uy} \ayrıldı ( X_{bilgisayar bilimi} + e_{x} – X_{IC} \sağ)\)
\(M_{sen} = -0 kip sol ( 1.5 içinde +0 içinde – 1.5 sağda) + 41 kip sol ( 1.5 içinde +4 içinde – 0.06 sağda)\)
\(M_{sen} = -222 tavuk-in)
Sonraki, hesaplananları karşılaştıralım Pux, Pux, ve Msen cıvata grubunun reaksiyonlarına.
\(P_{ux} \yaklaşık – \toplam R_{x}\)
\(P_{uy} \yaklaşık – \toplam R_{Y}\)
\(M_{sen} \yaklaşık – \toplam M_{sen}\)
Sol taraf denklemin sağ tarafına neredeyse eşit olduğundan, I.C'nin varsayılan konumu diyebiliriz.. doğru!
C katsayısı için çözme
I.C bir kez. konum belirlenir, şimdi aşağıdaki formülle cıvata grubu katsayısı C'yi alabiliriz.
\(C = frak{P_{sen}}{\fi R_{n}} = \frac{40.703 kip}{24.4 kip} = 1.668\)
Ücretsiz Cıvata Grubu Hesaplayıcı
Cıvatalı bağlantılarımızı bu yaklaşımla nasıl tasarladığımızı kontrol edin. Ücretsiz Çelik Bağlantı Tasarım Hesaplayıcısı! Daha fazla işlevsellik için, başlamak için bugün Structural 3D yazılımımıza kaydolun!


