Belirsiz Bir Kiriş Nasıl Hesaplanır – Çift İntegral Yöntemi

belirsiz kirişler reaksiyonları çözmek için gereken ekstra adımlar nedeniyle zor olabilir. Belirsiz yapıların bir belirsizlik derecesi denilen şeye sahip olduğunu unutmayın.. Yapıyı çözmek için, sınır koşulları getirilmelidir. Dolayısıyla, belirsizlik derecesi ne kadar yüksekse, daha fazla sınır koşulu tanımlanmalıdır. Ama belirsiz bir ışını çözmeden önce, önce kirişin statik olarak belirsiz olup olmadığını belirlememiz gerekiyor. Kirişler tek boyutlu yapılar olduğundan, harici olarak statik olarak belirsiz yapıları belirlemek için denklemi kullanmak yeterlidir.

[matematik]
ben_{e}=R-sol ( 3+e_{c} \sağ )
[matematik]

Nerede:

• ben_e = Belirsizlik derecesi
• R = Toplam reaksiyon sayısı
• e_c = Dış koşullar (Örneğin. iç menteşe)

Tipik, ancak, belirsizlik derecesini çözmeye gerek kalmadan, basit açıklıklar veya konsol kirişler dışındaki herhangi bir şey statik olarak belirsizdir, bu tür kirişlerin iç menteşelerle gelmediğini varsayarsak.

Belirsiz kirişlerin çözümüne yaklaşmanın birçok yolu vardır.. Her ne kadar SkyCiv Beam ile basitlik ve benzerlik adına el hesaplamaları, Çift Entegrasyon yöntemini tartışacağız.

Çift Entegrasyon

Çift Entegrasyon, belki de kirişlerin analizi için tüm yöntemlerin en basitidir.. Bu yöntemin konsepti, temel olarak integral hesabın temel bir anlayışına dayandığından diğer yöntemlerin aksine oldukça basittir., dolayısıyla adı. Kirişin eğriliği ile aşağıda gösterilen moment arasındaki ilişkiden bir miktar integral hesabı uyarlanmıştır..

[matematik]
\çatlamak{1}{\rho}= frac{M}{HAYIR}
[matematik]

1/ρ'nin kirişin eğriliği ve ρ'nın eğrinin yarıçapı olduğuna dikkat edin.. Temelde, eğriliğin tanımı, teğetin yay uzunluğuna göre değişim oranıdır.. Moment, elemanın uzunluğuna göre yüklemenin bir fonksiyonu olduğundan, elemanın uzunluğuna göre eğriliği entegre etmek, kirişin eğimini verecektir.. benzer şekilde, elemanın uzunluğuna göre eğimi entegre etmek, kiriş sapmasını verecektir.. Tipik yapısal yükler doğada cebirsel olduğundan, bu ifadelerin entegrasyonu, genel güç formülünü kullanmak kadar basittir.

[matematik]
\int fsol ( x sağ )^{n}dx=frac{fsol ( x sağ )^{n+1}}{n+1}+C
[matematik]

Belki de kavramı anlamanın en iyi yolu, aşağıdaki verilen bir kiriş örneği vermektir..

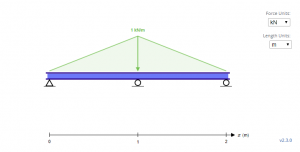
Yukarıdaki örnek kiriş, üçgen yüklemelere sahip belirsiz bir kiriştir.. İle destekler, Bir_Y, B_Y ve C_Y İlk için, ikinci, ve sırasıyla üçüncü destekler, Bu bilinmeyenleri çözmenin ilk adımı denge denklemleriyle başlamaktır..

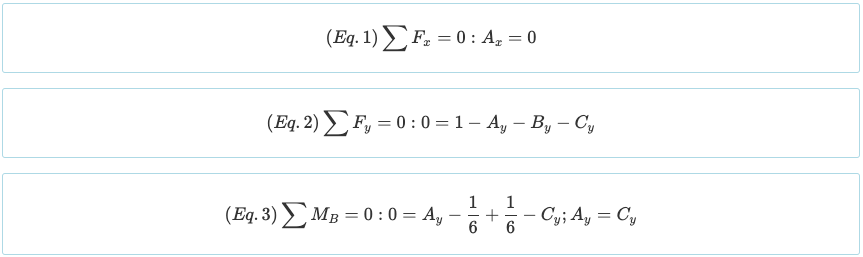
Kirişin bir dereceye sahip olduğuna dikkat edin. statik belirsizlik 1°. Dört bilinmeyen olduğu için (Bir_x, Bir_Y, B_Y, ve C_Y) ve yukarıdaki denge denklemlerinden şimdiye kadar üç denklem var, sınır koşullarından bir denklem daha oluşturmak gerekir. Nokta yük ve üçgen yük tarafından oluşturulan momentin aşağıdaki gibi olduğunu hatırlayın..

Nokta Yükü:

[matematik]
M=Fçax x; M = Fx
[matematik]

Üçgen Yük:

[matematik]
M=frak{w_{0}\çarpı x}{2}\kez kaldı ( \çatlamak{x}{3} \sağ ); M = frak{w_{0}x^{2}}{6}
[matematik]

Çift entegrasyon yöntemi kullanılarak, bu yeni denklemler yapılır ve aşağıda gösterilir.

Not: Yukarıdaki denklemler, bir ifadenin sıfıra eşit olduğu durumlarda Macaulay fonksiyonları olarak yazılmıştır. x < L. Bu durumda, L = 1.

Yukarıdaki denklemlerde, eklenen dördüncü terimin birdenbire ortaya çıktığına dikkat edin. Aslında, yükleme yönü yerçekimi yönünün tersidir. Bunun nedeni, üçgen yükleme denklemlerinin yalnızca uzunluk arttıkça yük arttığında çalışmasıdır.. Bu denklemler için çok fazla bir sorun değil dağıtılmış ve nokta yükleri simetrilerinden dolayı. Etkisinde, yukarıdaki kiriş için eşdeğer yükleme aşağıdaki kirişe benziyor, yani denklemler ona göre.

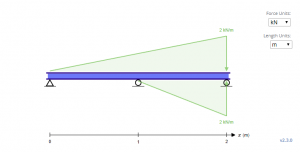
C'yi çözmek için₁ ve C₂, sınır koşulları belirlenmeli. Yukarıdaki ışında, bu tür üç sınır koşulunun mevcut olduğu gözlemlenebilir. x = 0, x = 1, ve x = 2, üç konumda sapma y sıfırdır.

Sınır koşulu 1

[matematik]
x=0, y = 0; C_{2}=0
[matematik]

Sınır koşulu 2

[matematik]
x=0, y = 0; C_{1}= frac{1}{120}-\çatlamak{bir_{Y}}{6}
[matematik]

Her bir sabitin değerlerini belirledikten sonra, son denklem artık son sınır koşulu kullanılarak elde edilebilir.

Sınır koşulu 3

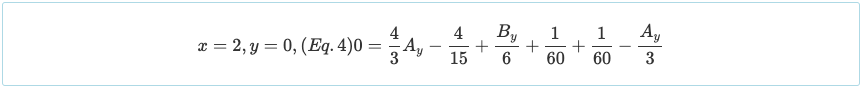
θ = sınır koşulunun 0 x = 1 kullanılabilir, simetrik yükleme ile simetrik bir sürekli kirişin sadece orta reaksiyonu için uygulanabilir olmasına rağmen.

Dört denklem belirlenirken, şimdi aynı anda çözülebilirler. Bu denklemlerin çözülmesi aşağıdaki reaksiyonları verecektir..

Belirlenen reaksiyonlarla, reaksiyonların değerleri, moment denklemine geri ikame edilebilir. Bu, kiriş sisteminin herhangi bir yerindeki momentin değerini belirlememizi sağlayacaktır..

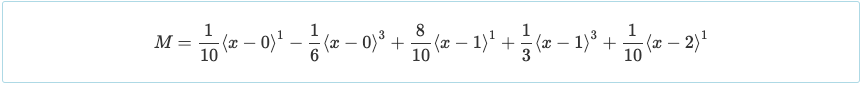
Çift Entegrasyonun bir başka kolaylığı da, moment denkleminin aşağıda gösterilen ilişki ile kesmeyi çözmek için kullanılabilecek bir şekilde sunulmasıdır..

[matematik]
V=frak{dM}{dx}
[matematik]

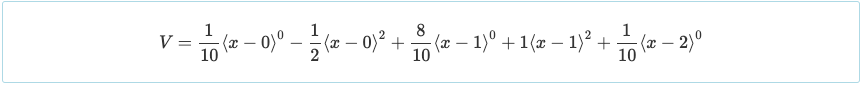
Tekrar, diferansiyel hesabın sadece temel bir anlayışını kullanarak, bir fonksiyonun türevini sıfıra eşitlemek, o fonksiyonun maksimum veya minimumunu verir. Böylece, eşitleme V = 0 maksimum pozitif bir an ile sonuçlanacaktır x = 0.447 ve x = 1.553 M = 0.030

Elbette, tüm bunlar SkyCiv Beam ile doğrulanabilir.

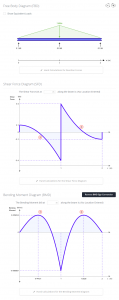
SkyCiv Beam Yazılımı

SkyCiv Işın Analiz Yazılımı kullanıcıların kiriş yapılarını kolay ve doğru bir şekilde analiz etmelerini sağlar. Işın üyenizin analizini alabilirsiniz, dahil olmak üzere reaksiyonlar, kesme kuvveti, bükülme anı, sapma, ve stresler birkaç saniye içinde.

Önce denemek istersen, Ücretsiz Kiriş Hesaplayıcı başlamak için harika bir yoldur, ya da bugün ücretsiz kaydolun!