Kesme/kayma gibi hesaplamalar için atalet momentinin gerekli olduğu durumlarda kiriş kesitlerinin ağırlık merkezi veya kütle merkezi kiriş analizi için kullanışlıdır.eğilme gerilimi ve sapma. Bu makale, centroid'in nasıl hesaplanacağına dair basit bir süreçte size rehberlik eder ve sizi SkyCiv Free Centroid Calculator ile tanıştırır.
Centroid Nasıl Bulunur?
Her şeyden önce, merkezini nasıl bulacağını bilmen gerek. Kiriş bölümleri genellikle bir veya daha fazla şekilden oluşur. Böylece, tüm bir ışın kesiti alanının ağırlık merkezini bulmak için, önce uygun bölümlere ayrılması gerekir. Bundan sonra, tüm bölümün ağırlık merkezini bulmak için her bir segmentin alanı ve ağırlık merkezi dikkate alınmalıdır.
Aşağıda gösterilen I-kiriş bölümünü düşünün. Dikey ağırlık merkezini hesaplamak için (y yönünde) bölünebilir 3 gösterildiği gibi segmentler:
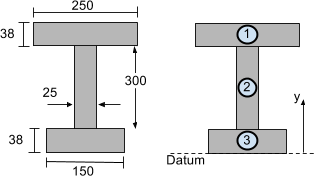
Şimdi düşey noktayı bulmak için ağırlık merkezi denklemini kullanmamız gerekiyor. (Y) çok parçalı şeklin ağırlık merkezi:

Referans veya referans çizgisini kiriş bölümünün altından alacağız.. Şimdi A'yı bulalımben ve yben yukarıda gösterilen I-kiriş bölümünün her segmenti için dikey veya y centroid bulunabilir.
[matematik]
\Metin{Bölüm 1:}\\
\başla{hizalamak}
{Bir}_{1} &= 250 times38 = 9500 {\Metin{ mm}}^{2}\\
{Y}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \Metin{ mm}\\\\
\son{hizalamak}
[matematik]
[matematik]
\Metin{Bölüm 2:}\\
\başla{hizalamak}
{Bir}_{2} &= 300 times25 = 7500 {\Metin{ mm}}^{2}\\
{Y}_{2} &= 38 + \tfrac{300}{2} = 188 \Metin{ mm}\\\\
\son{hizalamak}
[matematik]
[matematik]
\Metin{Bölüm 3:}\\
\başla{hizalamak}
{Bir}_{3} &= 38 times150 = 5700 {\Metin{ mm}}^{2}\\
{Y}_{3} &= tfrac{38}{2} = 19 text{ mm}\\\\
\son{hizalamak}
[matematik]

Kesitin iki malzemeden veya bir kompozit malzemeden oluşması durumunda, daha sonra malzemelerden birinin modüler oranla çarpılması gerekecektir, böylece denklem tüm bölüm üniform hale gelir..
[matematik]
n = frac{E_{1}}{E_{2}}
[matematik]
Tipik, E1 baskın olmayan malzemenin esneklik modülüdür, ve E2 hakim malzemenin esneklik modülüdür, hangi sıra tercih edilirse edilsin centroidin çözümünü etkilemeyecektir.. İkinci malzeme için ayarlama, centroid denklemi aşağıdaki gibi olur.
[matematik]
\bar{Y}= frac{\toplam{Bir}_{ben}{Y}_{ben}+\toplam {n}{Bir}_{ben}{Y}_{ben}}{\toplam{Bir}_{ben}+\toplam {n}{Bir}_{ben}}
[matematik]
SkyCiv ile ışının ağırlık merkezini bulun
Kirişin ağırlık merkezini bulmak önemlidir ancak bunların elle hesaplanması zaman alıcı olabilir. SkyCiv'in sunduğu bir Ücretsiz Centroid Hesap Makinesi bu süreci sizin için otomatikleştiren, dikeyi bulmanıza yardımcı olur (Y) ve yatay (x) kiriş kesitlerinin ağırlık merkezleri kolay ve doğru bir şekilde!
Bu araç ücretsiz bir sürümüdür SkyCiv Bölüm Oluşturucu, geometrik analiz için kapsamlı bir çevrimiçi kesit analiz yazılımı, bükme, kesme ve burulma kesit özellikleri ile FEA ve betonarme tasarım. Bu araçla, önceden tanımlanmış şablonları kullanarak özel bölümler oluşturabilir veya noktalarla kendi şekillerinizi tanımlayabilirsiniz, çizgiler, veya CAD'den DXF içe aktarmaları.
Tüm işlevleri keşfetmek için SkyCiv Bölüm Oluşturucu kesitinizi modellemenin ve analiz etmenin kolaylığını yaşayın, bugün ÜCRETSİZ kaydolun!
Alakalı kaynaklar


