Frekans analizinin tanımı?
Binaları tasarlarken, iki tane yük türleri değerlendırmek: statik ve dinamik. ilki için, sadece yapının uygulanan kalıcı yüklere karşı doğrudan tepkisinin yer değiştirme ve gerilmeler cinsinden hesaplanması gerekmektedir.. Bu, Sertlik veya Sonlu Elemanlar Yöntemi kullanılarak elde edilebilir..
Dinamik analiz durumunda, zamana bağlı yükler nedeniyle yapının tepkisindeki olası varyasyonların aralığını dikkate almak daha zordur.. Bu nedenle, bazı yeni araçlar veya işlevler analize dahil edilmek için gerekli hale gelir. Yani, frekans analizi, titreşim mekaniğinde temel bir yöntem, doğar.
Bu yöntem, uygulanan dinamik yükler nedeniyle yapı hareketinin zaman içindeki değişimini elde eder.. Daha spesifik olarak, bu, iç kuvvetleri hesaplamak için yapısal sistemin titreşiminin doğal özelliklerinin kullanılması anlamına gelir., yer değiştirmeler, kararlılık sorunları, vb.
Konu hakkında daha fazla bilgi için, nasıl gerçekleştirileceğini kısaca açıklayan bir SkyCiv makalesini okumanızı öneririz. Dinamik Frekans Analizi kullanma SkyCiv Yapısal Analiz Yazılımı.
Frekans analizi neden tasarımla ilgilidir??
Bir tasarımda frekans analizinin önemini ölçmenin en iyi yolu, kötü dinamik davranış nedeniyle başarısız olan bazı yapıların durumunu izlemektir.. Kuzey Amerika'daki ünlü köprülerden biri Tacoma Narrows'dur., rüzgarın neden olduğu sürekli periyodik titreşimlerden sonra nihayet çöktü. Aşağıdaki resimler, çökmeden hemen önce köprü boyunca artan yer değiştirmeyi gösterecektir., öncelikle karayoluna odaklanmış:

şekil ben. Tacoma Narrows Bridge'de yanal burulma titreşimleri

Şekil ii. Çökmeden önce Köprüde artan yer değiştirme.

Şekil iii. Feci Köprü Çöküşü
Bu vaka çalışmasında, Uygun bir frekans analizi yapılmamış ve yapı, yapının doğal frekansını dikkate alacak şekilde yeterince tasarlanmamıştır..
basit sarkaç
Frekans analizi, bir yapının dış dinamik eylemlere maruz kaldığında geliştirdiği farklı biçimleri inceler.. Bu yüzden birkaç farklı elde edersiniz modlar. Daha sonra bu formları kullanarak, dengeyi garanti etmek için gereken iç kuvvetler aracılığıyla yapının eleman boyutlarını belirleyebiliriz.
Frekans analizi için teknik ve matematiksel hususlara derinlemesine girmeden önce, Şekil iv'de gösterilen bir sarkaç kolonunun bir sonraki basit sistemini gözden geçirin.
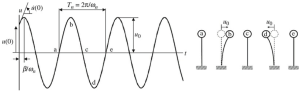
Şekil IV. Serbest titreşim sarkaç sisteminin dinamik tepkisi
Son resimde gösterildiği gibi basit bir analiz kullanarak, sarkaç kolonu için üst kütlenin hareketini her seferinde tanımlayabiliriz.. Bu makalenin temel amacı, iki tipik durum için frekans analizini ele almak olacaktır., tek ve çoklu serbestlik derecesi.
Tek serbestlik derecesi
Bu özel durum, dinamik analiz için en basit olanıdır.. Davranış, D'Alembert'in denge yasası kullanılarak tanımlanır., ikinci Newton yasasının bir uzantısı.
Aşağıdaki şekil, SDOF sisteminin öğelerini göstermektedir., sertlik (k), sönümleme (c), ve kütle kaynağı (m) atalet kuvvetleri için. Kütleye uygulanan zamanla değişen dış kuvvet şu şekilde temsil edilir: \({p(t)}\).
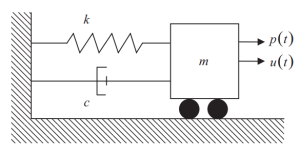
Figür 1. Tek Serbestlik Derecesi (SDOF) sistem. (Tas, 2017, sayfa 56)
Tüm elemanlar dinamik denge koşulunu sağlamalıdır.:
\({m}{\nokta{sen}}+{c}{\nokta{sen}}+{k}{sen}={p(t)}\)
Bu doğrusal ikinci dereceden bir diferansiyel denklemdir, ve çözümünün iki bileşeni vardır:
\({sen(t)}={sen}_{h}(t)+{sen}_{p}(t)\)
Nerede:
- \({sen(t)}\) mutlak yer değiştirme.
- \({sen}_{h}(t)\) homojen çözüm, genellikle serbest titreşim durumunu içerir.
- \({sen}_{p}(t)\) uygulanan uyarıma göre özel çözümdür.
Titreşim davranışını ve bir yapının sahip olduğu en kritik dinamik özellikleri açıklamak için yalnızca homojen çözüme odaklanacağız..
Aşağıdaki terimleri tanımlayalım:
\({\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{n}}={\sqrt(\çatlamak {k}{m})}\) Açısal frekans
\({\xi}={\çatlamak{c}{{2}{m}{\omega_n}}}={\çatlamak{c}{{2}{\sqrt(\çatlamak {k}{m})}}}\) Kritik sönüm oranı
Kritik sönüm oranı, 1, titreşim durumu düşük sönümlenecektir; yani, hareket durmadan önce tamamlanmış döngüler olacak.
Çözüm aşağıdaki genel formdadır
\({u_h}={e^{{-\xi}{\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{n}}{t}}}{[{Bir}{çünkü}{\omega_d}{t}+{B}{olmadan}{\omega_d}{t}]}\)
Nerede:
- A ve B, hareketin başlangıç koşullarına bağlı olan entegrasyon sabitleridir..
- \({\omega_d}={\omega_n}{\sqrt({{1}-{\xi^2}})}\) sönümlü açısal frekans
A ve B sabitlerini değerlendirdikten sonra, sönümsüz durum için genel çözüm
\({u_h}={e^{{-\xi}{\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{n}}{t}}}{[{u_0}{çünkü}{\omega_d}{t}+{\çatlamak{{\nokta{u_0}}+{\xi}{\omega_n}{u_0}}{\omega_d}}{olmadan}{\omega_d}{t}]}\)
Nerede:
- \({u_0}\) kütle başlangıç yer değiştirmesidir
- \(\nokta{u_0}\) kütle başlangıç hızıdır
Başlangıç koşullarının bazı değerleri ile çözümü çizersek, aşağıdaki rakamı elde edeceğiz.
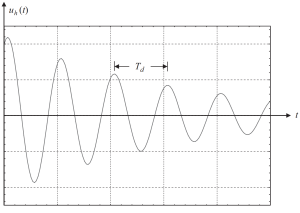
Figür 2. Yer değiştirme, kritik altı sönümlü bir durumda çözümün homojen bir parçasıyla sonuçlanır. (Tas, 2017, sayfa 58)
diğer durumda, kritik sönümleme fraksiyonunun bir değeri olduğunda ne olduğunu analiz etmek çok önemlidir. 1. \({\xi}=1). Bu durum, tam sönümlemeli bir yapıyı ifade eder..
Kullanılacak denklem
\({u_h}={e^{{-\Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{n}}{t}}}{\{u_0+({\nokta{u_0}}+{\omega_n}{u_0}){t}}\}\)
Ve farklı başlangıç koşulları durumlarını gösteren grafikleri aşağıdaki görseldedir..
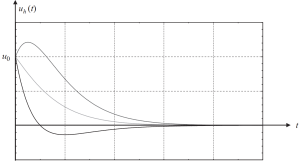
Figür 3. Yer değiştirme, kritik sönümlü bir durumda çözümün homojen bir parçasıyla sonuçlanır. (Tas, 2017, sayfa 58)
Yanıt parametreleri
Önceki bölüm, bir SDOF sisteminde serbest dinamik titreşim için çözümü tanımlamamıza yardımcı oldu.. İki ana parametre doğal frekanstır. \(\omega_n\) yapının kendi kendine nasıl titreyeceğini gösterir, ve kritik sönüm oranı \(\xi), çürüyen titreşimlerdeki hızı tanımlayan.
Genel olarak, yapıların maksimum değeri ile düşük sönüm vardır \(\xi)=10 %. Bu değeri kullanarak sönümlü doğal frekansı değerlendirirsek, sonuç \({\omega_d}=0.995{\omega_n}\). Yani, kullanılması tavsiye edilir \({\omega_d}{\kalın yaklaşık}{\omega_n}\).
Dinamik özellikleri aşağıdaki tabloda özetleyebiliriz.
| Açısal frekans (rad/s) | Doğal frekans (Hz.) | Doğal dönem (s) | |
|---|---|---|---|
| Açısal frekans \({\omega_n}\) | \({\omega_n}\) | \(2{\pi}{f_n}\) | \(\çatlamak{2{\pi}}{T_n}\) |
| Doğal frekans \({f_n}\) | \(\çatlamak{\omega_n}{2{\pi}}\) | \(f_n\) | \(\çatlamak{1}{T_n}\) |
| Doğal dönem \({T_n}\) | \(\çatlamak{2{\pi}}{\omega_n}\) | \(\çatlamak{1}{f_n}\) | \(T_n\) |
Tablo 1. Açısal frekans arasındaki ilişki, doğal frekans, ve dönem (Tas, 2017, sayfa 60)
Birden fazla serbestlik derecesi
Bir yapıda birçok kütle olduğunda, bu kütleler için herhangi bir zamanda konumu tanımlamak için birden çok koordinat tanımlamamız gerekir.. Belirli ve bariz bir örnek aşağıdaki şekilde gösterilmektedir., her hareket anında konumu belirlemek için farklı açıların gerekli olduğu karmaşık bir sarkaçtan oluşan.
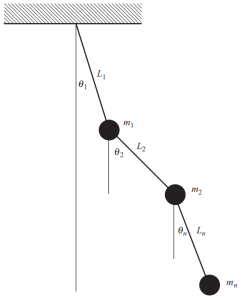
Figür 4. Çoklu kütleli sarkaç. (Tas, 2017, sayfa 53)
Bu bölümde, yapıları analiz ediyoruz’ birden çok serbestlik derecesi için özelliklerin genişletilmesi frekans analizini kullanan genel dinamik yanıt.
Gerçek bir yapıyla uğraşırken modelleme sürecinin farkında olmak zorunludur.. Aşağıdaki resimler, dinamik tepkisini açıklamak için frekans analizini uygulamaya hazır bir matematiksel model oluşturmak için gerekli adımları açıklamaktadır..
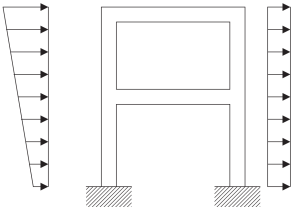
Figür 5. Sürekli bir yapısal çerçevenin fiziksel modeli. (Tas, 2017, sayfa 23)
İlk adım, kirişlerin ve kolonların her seviyedeki kesişme noktalarında kütleleri bir araya getirmeyi içerir.. Her düğümün üç olası hareketi vardır, iki doğrusal yer değiştirme, ve bir dönüş. Analizde tutarlı olmak, kütleler ve polar atalet özellikleri dikkate alınmalıdır.
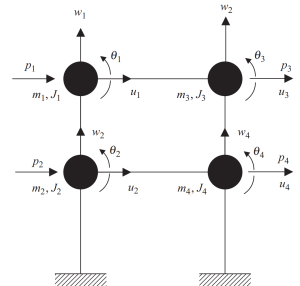
Figür 6. Yer değiştirme ve dönme serbestlik derecesine sahip düğüm noktalarında toplanmış kütleler. Ayrık Sistem. (Tas, 2017, sayfa 23)
Statik yoğunlaştırma yöntemi, analizin karmaşıklığını azaltmaya yardımcı olabilir, dönme ve öteleme eylemsizliğinin ihmal edilmesi.
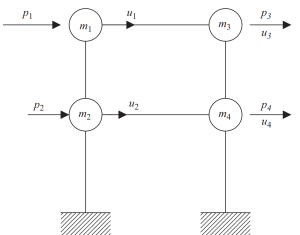
Figür 7. Serbestlik derecesinin yalnızca yatay yer değiştirmeye statik yoğunlaşması. (Tas, 2017, sayfa 23)
son adımda, bu çerçeve örneği için yatay hareketi yalnızca iki düğümde toplayabiliriz.
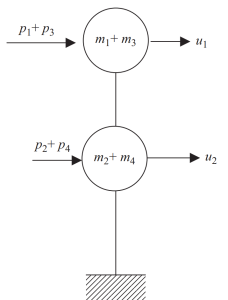
Figür 8. İki düğüm noktasında nihai statik yoğunlaşma ve yatay yer değiştirme serbestlik derecesi. (Tas, 2017, sayfa 24)
Önceki bölümde SDOF sistemi ile yaptığımız gibi, çoklu serbestlik dereceleri için hareket denkleminin çözümünü geliştireceğiz.
Hareket denklemi matris formunda şu şekilde yazar:
\([M]\{\nokta{sen}\} + [C]\{\nokta{sen}\}+[K]\{sen}={p(t)}\)
Nerede:
- \([M]\) kütle matrisidir
- \([C]\) Coulumb'un sönümleme matrisidir
- \([K]\) bu sertlik matrisi
Tepki parametrelerini elde etmek için serbest titreşim çözümünü çalışmalıyız.. Sisteme herhangi bir sönüm ve kuvvet uygulanmaz., sadece başlangıç koşulları değerlendirilecek.
\([M]\{\nokta{sen}\} +[K]\{sen}={0}\)
Bir SDOF için ilk duruma benzer şekilde, formunun sinüzoidal bir çözümünü test edebiliriz..
\({sen(t)}={\fi}{({a}{çünkü}{\omega}{t}+{b}{olmadan}{\omega}{t})}\)
\({\nokta{sen}{(t)}}={-{\omega}^ 2}{\fi}{({a}{çünkü}{\omega}{t}+{b}{olmadan}{\omega}{t})}\)
hangi vektörde \(\fi) zamana bağlı olarak değişmeyen bir şekil vektörüdür.. katsayılar “a” ve “b” başlangıç koşulları değerlendirilirken elde edilen sabitlerdir.
Test çözümü için her iki ifadeyi hareket denkleminde değiştirdikten sonra, doğrusal özdeğer-özvektör problemini elde ederiz:
\([K]{\fi}={{\omega}^ 2}[M]{\fi}\)
Nerede:
- \({{\omega}^ 2}\) özdeğerler kümesidir
- \({\fi}\) özvektörlerin kümesidir
Son şekillerdeki çerçeve örneği için bu klasik sorunun çözümü, kütlelerin nasıl titreşeceğini göstermektedir.. Bu, her kütlenin özvektörlerin değerine göre yatay yönde hareket edeceği anlamına gelir..
Bu davranışın aşağıdaki görüntüsüne bakın.
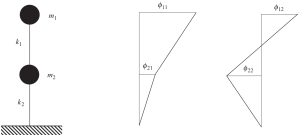
Şekil No.9. İki özvektör sonucunu gösteren frekans analizi. (Tas, 2017, Sayfa 135)
SkyCiv Yapısal 3D
İle yapılarınız için frekans analizi yapın SkyCiv Yapısal 3D. Başlamak için bugün kaydolun!
Referanslar:
- Eduardo Kausel, (2017). “Gelişmiş Yapısal Dinamikler” 1birinci baskı, Cambridge Üniversitesi Yayınları


