NBCC'nin tamamen işlenmiş bir örneği 2015 NBCC'nin tamamen işlenmiş bir örneği

NBCC'nin tamamen işlenmiş bir örneği. NS NBCC'nin tamamen işlenmiş bir örneği (2015) B Bölümü – Bölüm 4.1.6 NBCC'nin tamamen işlenmiş bir örneği. NBCC'nin tamamen işlenmiş bir örneği, NBCC'nin tamamen işlenmiş bir örneği (S3D) NBCC'nin tamamen işlenmiş bir örneği, Aşağıda gösterildiği gibi:

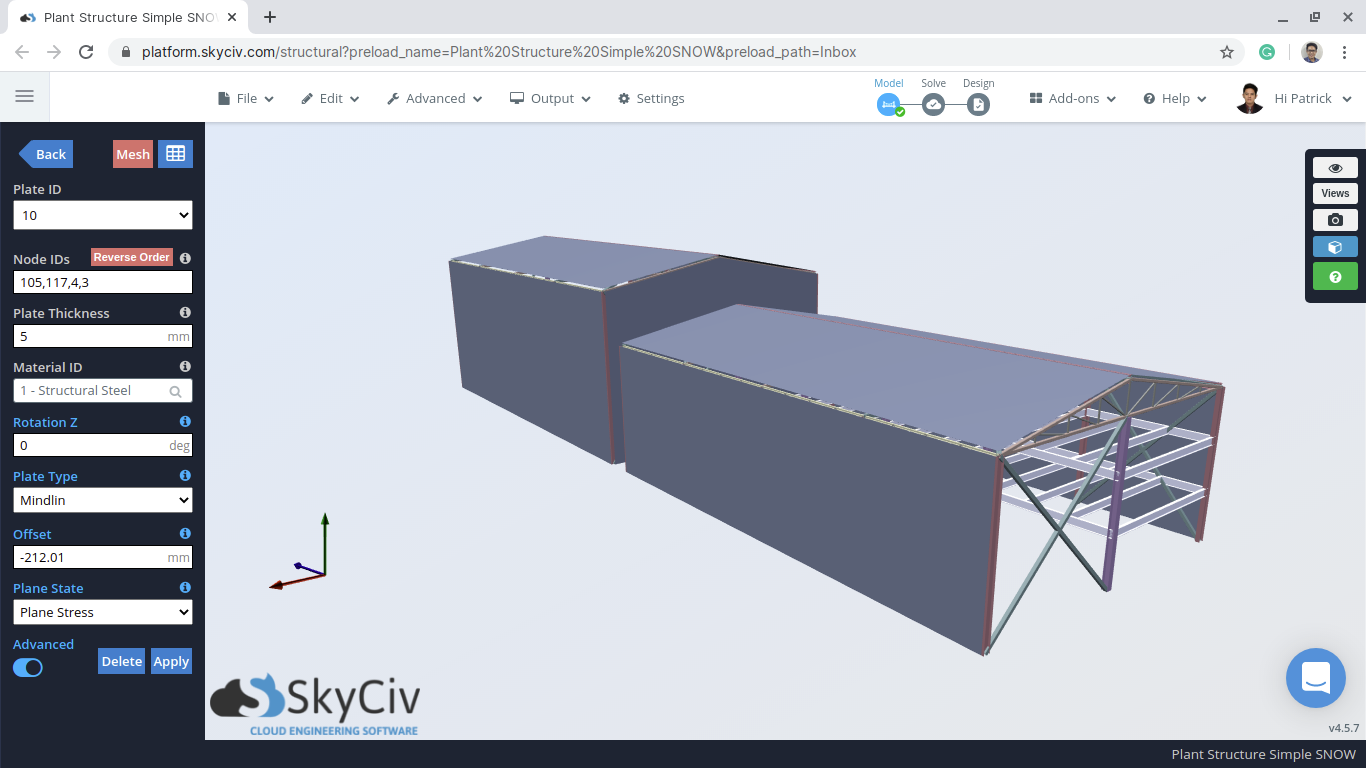
Figür 1: NBCC'nin tamamen işlenmiş bir örneği

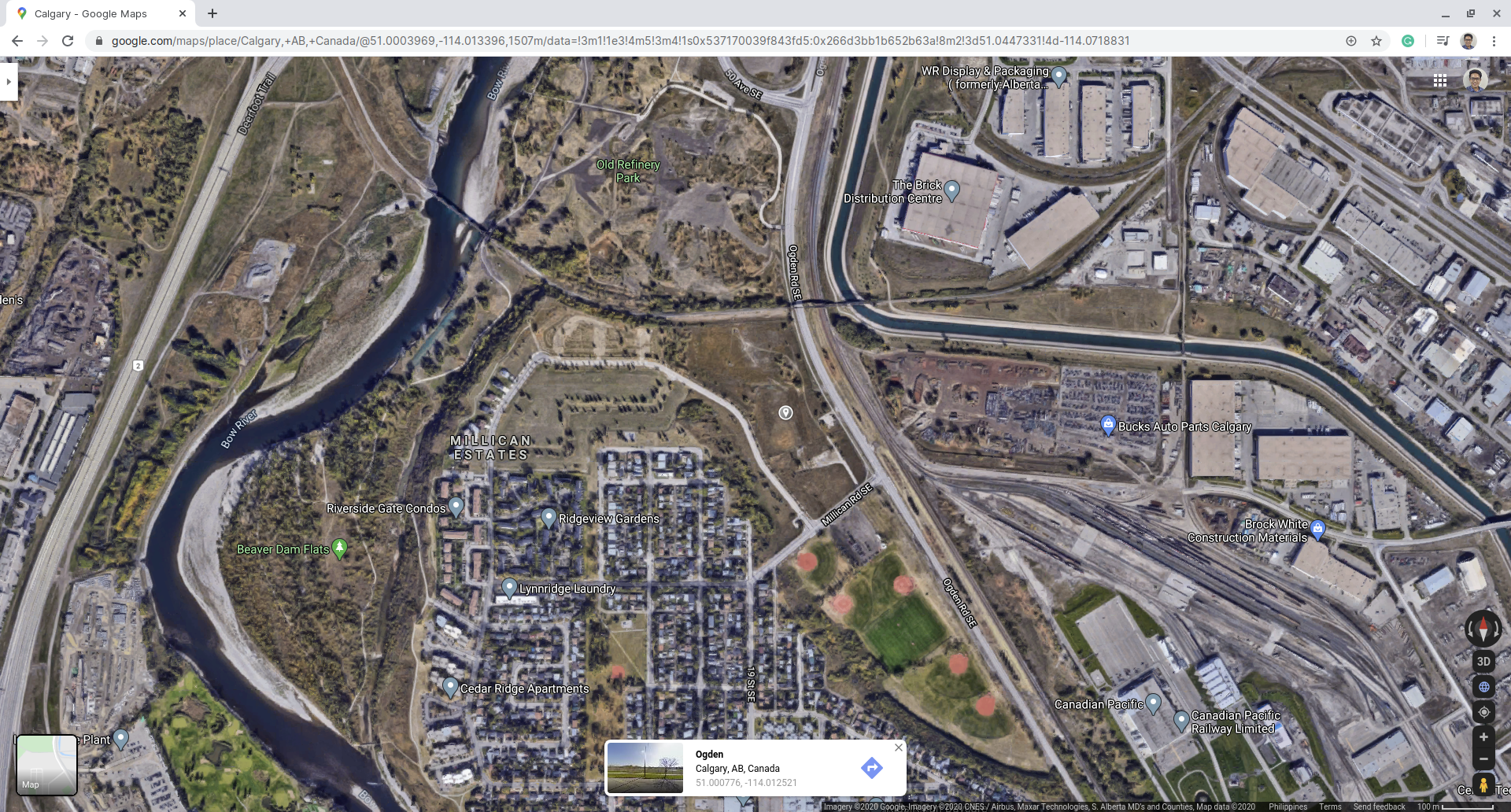
Figür 2: NBCC'nin tamamen işlenmiş bir örneği (NBCC'nin tamamen işlenmiş bir örneği).

Tablo 1: NBCC'nin tamamen işlenmiş bir örneği.

yer	NBCC'nin tamamen işlenmiş bir örneği, NBCC'nin tamamen işlenmiş bir örneği, NBCC'nin tamamen işlenmiş bir örneği (NBCC'nin tamamen işlenmiş bir örneği)
Doluluk	NBCC'nin tamamen işlenmiş bir örneği
Boyutlar	19.508 NBCC'nin tamamen işlenmiş bir örneği 31.70 NBCC'nin tamamen işlenmiş bir örneği NBCC'nin tamamen işlenmiş bir örneği 9.144 m NBCC'nin tamamen işlenmiş bir örneği 11.941 m NBCC'nin tamamen işlenmiş bir örneği 3.50 m NBCC'nin tamamen işlenmiş bir örneği 16°
NBCC'nin tamamen işlenmiş bir örneği	NBCC'nin tamamen işlenmiş bir örneği NBCC'nin tamamen işlenmiş bir örneği 2.30 m

Tablodan 1, NBCC'nin tamamen işlenmiş bir örneği, \(S), formül kullanılarak hesaplanabilir:

\(formül kullanılarak hesaplanabilir {ben}_{s}[{S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{a} +{S}_{r}]\) (1)

Nerede:

\({ben}_{s}\) formül kullanılarak hesaplanabilir, formül kullanılarak hesaplanabilir
\({S}_{s}\) = 1-formül kullanılarak hesaplanabilir, kPa, formül kullanılarak hesaplanabilir 1.1.3
\({C}_{b}\) formül kullanılarak hesaplanabilir, 4.1.6.2 (2)
\({C}_{w}\) formül kullanılarak hesaplanabilir, 4.1.6.2 (3) ve (4)
\({C}_{s}\) formül kullanılarak hesaplanabilir, 4.1.6.2 (5), (6), ve (7)
\({C}_{a}\) formül kullanılarak hesaplanabilir, 4.1.6.2 (8)
\({S}_{r}\) formül kullanılarak hesaplanabilir, kPa, formül kullanılarak hesaplanabilir 1.1.3, formül kullanılarak hesaplanabilir \({S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{a}\)

formül kullanılarak hesaplanabilir. formül kullanılarak hesaplanabilir: formül kullanılarak hesaplanabilir (formül kullanılarak hesaplanabilir), formül kullanılarak hesaplanabilir.

Önem Faktörü, \({ben}_{s}\)

formül kullanılarak hesaplanabilir, \({ben}_{s}\), formül kullanılarak hesaplanabilir formül kullanılarak hesaplanabilir formül kullanılarak hesaplanabilir. formül kullanılarak hesaplanabilir, formül kullanılarak hesaplanabilir Düşük. Dahası, hesaplama Nihai Limit Durumunda olacaktır (ULS). hesaplama Nihai Limit Durumunda olacaktır formül kullanılarak hesaplanabilir, \({ben}_{s}\) eşittir 0.80.

Önem Kategorisi	Önem Faktörü, \({ben}_{s}\)
	ULS	SLS
Düşük	0.8	0.9
Normal	1.0	0.9
Yüksek	1.15	0.9
hesaplama Nihai Limit Durumunda olacaktır	1.25	0.9

Zemin Kar Yükü, \({S}_{s}\), hesaplama Nihai Limit Durumunda olacaktır, \(({S}_{r})\)

hesaplama Nihai Limit Durumunda olacaktır, \({S}_{s}\), hesaplama Nihai Limit Durumunda olacaktır, \(({S}_{r})\), hesaplama Nihai Limit Durumunda olacaktır hesaplama Nihai Limit Durumunda olacaktır, hesaplama Nihai Limit Durumunda olacaktır 2015 hesaplama Nihai Limit Durumunda olacaktır. Bu örnek için, karşılık gelen \({S}_{s}\) ve \(({S}_{r})\) içinde hesaplama Nihai Limit Durumunda olacaktır eşittir 1.10 kPa ve 0.1 kPa, sırasıyla.

hesaplama Nihai Limit Durumunda olacaktır 2015? Deneyin NS hesaplama Nihai Limit Durumunda olacaktır hesaplama Nihai Limit Durumunda olacaktır \({S}_{s}\) ve \({S}_{r}\) hesaplama Nihai Limit Durumunda olacaktır.

SkyCiv Kar Yükü Hesaplayıcı

hesaplama Nihai Limit Durumunda olacaktır, \({C}_{w}\)

hesaplama Nihai Limit Durumunda olacaktır, \({C}_{w}\), hesaplama Nihai Limit Durumunda olacaktır 1.0 dayalı 4.1.6.2 (3). hesaplama Nihai Limit Durumunda olacaktır 4.1.6.2 (4) hesaplama Nihai Limit Durumunda olacaktır. Bu örnek için, \({C}_{w}\) eşit olacaktır 1.0 hesaplama Nihai Limit Durumunda olacaktır.

hesaplama Nihai Limit Durumunda olacaktır, \({C}_{b}\)

hesaplama Nihai Limit Durumunda olacaktır, \({C}_{b}\), hesaplama Nihai Limit Durumunda olacaktır, referans olarak 4.1.6.2 (2):

\({C}_{b} = 0.8\) (2) için \({l}_{c} ≤ (70/{{C}_{w}}^{2})\) ve
\({C}_{b} = (1/{C}_{w}) [1 – (1 – 0.8{C}_{w})hesaplama Nihai Limit Durumunda olacaktır(-0.01({l}_{c}{{C}_{w}}^{2} – 70))] \) (3) için \({l}_{c} > (70/{{C}_{w}}^{2})\)

Nerede:

\({l}_{c}\) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu: \(2w -{w}^{2}/l\)
\(l\) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu
\(w\) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu

Bu örnek için,\(l\) ve \(w\) eşittir 31.7 m ve 19.51 m, sırasıyla, dolayısıyla, \({l}_{c}\) eşittir 27.01. Dan beri \({l}_{c}\) daha az \((70/{1.0}^{2})\), = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, \({C}_{b}\), eşittir 0.8.

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, \({C}_{s}\)

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu \({C}_{s}\) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu 4.1.6.2 (5), (6), ve (7) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu.

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu:

\({C}_{s} = 1.0\) için \(α ≤ 15°\)
\({C}_{s} = 0\) için \(a > 60°\)
\({C}_{s} = (60° – a)/45°\) için \(15° < α ≤ 60°\)

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu:

\({C}_{s} = 1.0\) için \(α ≤ 30°\)
\({C}_{s} = 0\) için \(a > 70°\)
\({C}_{s} = (70° – a)/40°\) için \(30° < α ≤ 70°\)

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, \(γ\)

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu 4.1.6.13 = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu:

\(y = 0.43{S}_{s} + 2.2 = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu{m}^{3} = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu{m}^{3}\) (4)

Bu örnek için, \(γ\) eşittir \(2.673 = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu{m}^{3}\).

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, \({C}_{a}\)

= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, \({C}_{a}\), yük durumuna bağlı olarak hesaplanır ayrıntılı olarak kabul ediliyor 4.1.6.2 (8). Bu değer, her durum için ayrıntılı olarak hesaplanacaktır..

Belirtilen Kar Yükü, \(S)

Bu bölümde, Belirtilen Kar Yükü, \(S), Belirtilen Kar Yükü.

Belirtilen Kar Yükü

Belirtilen Kar Yükü, NS Yapıların beşik çatılı olması nedeniyle \({C}_{a}\) eşittir 1.0. Dahası, çatı eğim açısı nedeniyle \(α\) dır-dir \(16°\) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, \({C}_{s}\), = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu 0.978. Denklemi kullanma (1), NBCC'nin tamamen işlenmiş bir örneği, \(S), Belirtilen Kar Yükü:

\(formül kullanılarak hesaplanabilir 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa

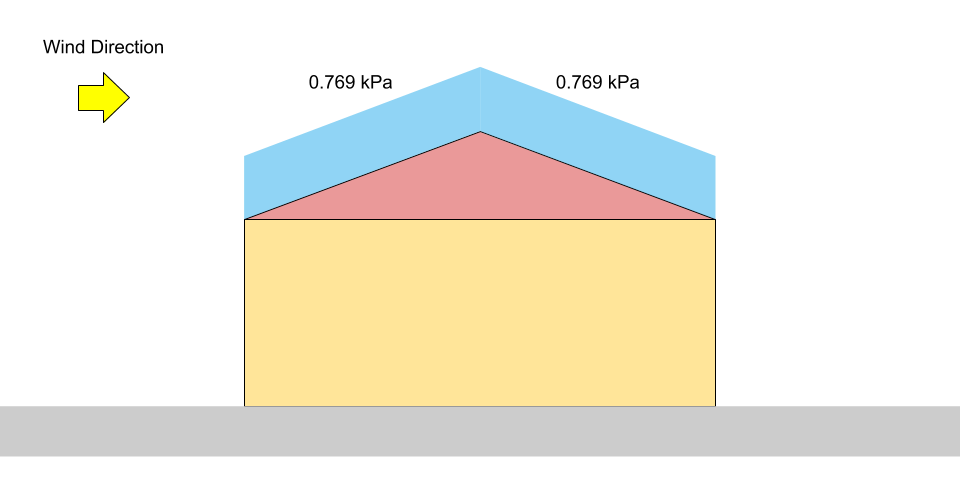
Figür 3: Belirtilen Kar Yükü.

Belirtilen Kar Yükü

Belirtilen Kar Yükü

Yapıların beşik çatılı olması nedeniyle, Yapıların beşik çatılı olması nedeniyle (Yapıların beşik çatılı olması nedeniyle) Yapıların beşik çatılı olması nedeniyle \({C}_{a}\) Yapıların beşik çatılı olması nedeniyle 4.1.6.9:

\({C}_{a, rüzgarın ters yönünde} = 0\)
\({C}_{a, rüzgar yönünde} = 0.25 +α/20\) için \(15° ≤ α ≤ 20°\)
\({C}_{a, rüzgar yönünde} = 1.25\) için \(20° < α ≤ 90°\)

Yapıların beşik çatılı olması nedeniyle, Yapıların beşik çatılı olması nedeniyle \({C}_{a, rüzgarın ters yönünde}\) ve \({C}_{a, rüzgar yönünde}\) Yapıların beşik çatılı olması nedeniyle 0 ve 1.05, sırasıyla. Dahası, çatı eğim açısı nedeniyle \(α\) dır-dir \(16°\) = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu, \({C}_{s}\), = olarak tanımlanan üst veya alt çatının karakteristik uzunluğu 0.978.

Belirtilen Kar Yükü, \({C}_{a}\) Belirtilen Kar Yükü 4.1.6.9 Belirtilen Kar Yükü. Belirtilen Kar Yükü, \({C}_{a, rüzgarın ters yönünde} = 0\) ve \({C}_{a, rüzgar yönünde} = 1.05\). Bu nedenle, Belirtilen Kar Yükü:

\({S}_{rüzgarın ters yönünde} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({p}_{1}\)
\({S}_{rüzgar yönünde} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({p}_{2}\)

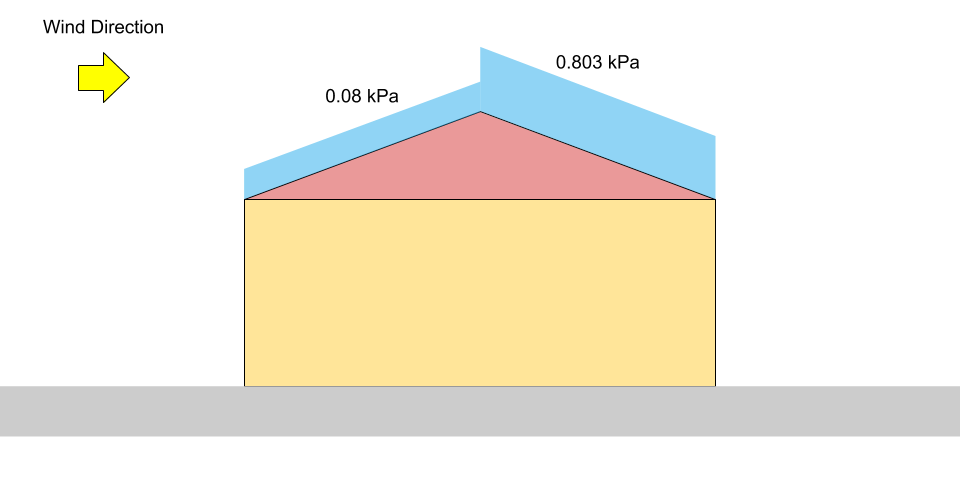
Figür 4: Belirtilen Kar Yükü (Belirtilen Kar Yükü).

Belirtilen Kar Yükü – = üst çatıdaki korkuluk yüksekliği – Belirtilen Kar Yükü

Yapıların beşik çatılı olması nedeniyle, Yapıların beşik çatılı olması nedeniyle. belirlemek için Yapıların beşik çatılı olması nedeniyle \({C}_{a}\), Yapıların beşik çatılı olması nedeniyle 4.1.6.2 (8) Yapıların beşik çatılı olması nedeniyle:

\({C}_{a} ={C}_{Yapıların beşik çatılı olması nedeniyle} – ({C}_{Yapıların beşik çatılı olması nedeniyle} – 1)(Yapıların beşik çatılı olması nedeniyle{x}_{d})\) için \(0 ≤ x ≤ {x}_{d}\)
\({C}_{a} = 1.0\) için \(x > {x}_{d}\)

Nerede:

\({C}_{Yapıların beşik çatılı olması nedeniyle}\) Yapıların beşik çatılı olması nedeniyle \({C}_{Yapıların beşik çatılı olması nedeniyle}\) x = 0
\(X) Yapıların beşik çatılı olması nedeniyle
\({x}_{d}\) Yapıların beşik çatılı olması nedeniyle 3 altında

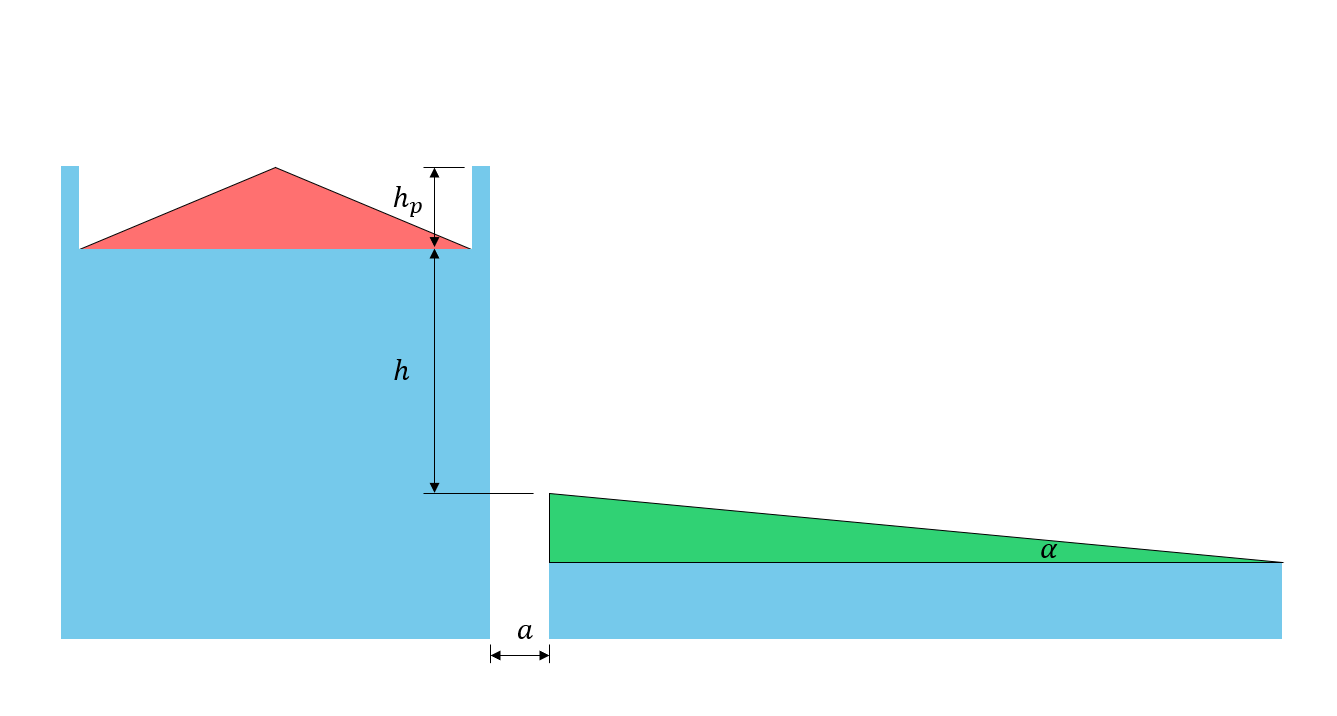
Figür 5: Yapıların beşik çatılı olması nedeniyle

 

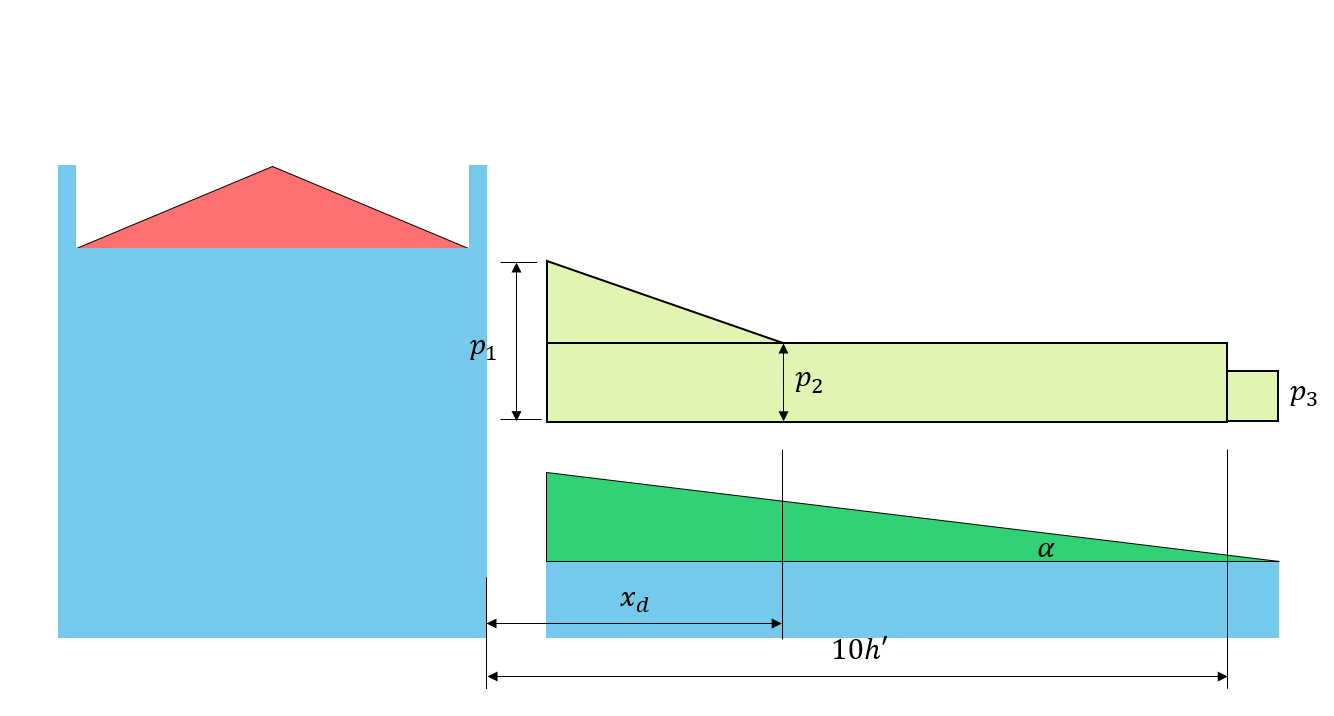
Figür 6: Yapıların beşik çatılı olması nedeniyle Yapıların beşik çatılı olması nedeniyle.

\({C}_{Yapıların beşik çatılı olması nedeniyle}\) ve \({x}_{d}\) hesaplama Nihai Limit Durumunda olacaktır:

\({C}_{Yapıların beşik çatılı olması nedeniyle} = frac{Yapıların beşik çatılı olması nedeniyle}{{C}_{b}{S}_{s}}\) veya \({C}_{Yapıların beşik çatılı olması nedeniyle} = frac{F}{{C}_{b}}\) (5), Yapıların beşik çatılı olması nedeniyle

\({x}_{d} = 5 \çatlamak{{C}_{b}{S}_{s}}{c}({C}_{Yapıların beşik çatılı olması nedeniyle} – 1)\) (6)

\(F = 0.35β\sqrt{\çatlamak{c({l}_{cs} – 5{{h}_{p}}^{'})}{{S}_{s}}} +{C}_{b}\) fakat \(Yapıların beşik çatılı olması nedeniyle 5\) için \({C}_{Yapıların beşik çatılı olması nedeniyle} = 1.0\) (7)

\({h}^{'} = h – \çatlamak{{C}_{b}{C}_{w}{S}_{s}}{c}\) (8)

\({{h}_{p}}^{'} ={h}_{p} – \çatlamak{0.8{S}_{s}}{c}\) fakat \(0 ≤ {{h}_{p}}^{'} ≤ \frac{{l}_{cs}}{5}\) (9)

Nerede:

\({h}_{p}\) = üst çatıdaki korkuluk yüksekliği (0 = üst çatıdaki korkuluk yüksekliği)
\(h) = üst çatıdaki korkuluk yüksekliği
\({C}_{Yapıların beşik çatılı olması nedeniyle}\) = üst çatıdaki korkuluk yüksekliği \({C}_{w}\) = üst çatıdaki korkuluk yüksekliği
\({l}_{cs}\) = üst çatıdaki korkuluk yüksekliği: \(2{w}_{s} -{{w}_{s}}^{2}/{l}_{s}\)
\({l}_{s}\) = üst çatıdaki korkuluk yüksekliği 7 ve 8, aşağıda gösterilen
\({w}_{s}\) = üst çatıdaki korkuluk yüksekliği 7 ve 8, aşağıda gösterilen
\(β\) = 1.0 = üst çatıdaki korkuluk yüksekliği, ve 0.67 = üst çatıdaki korkuluk yüksekliği.

 

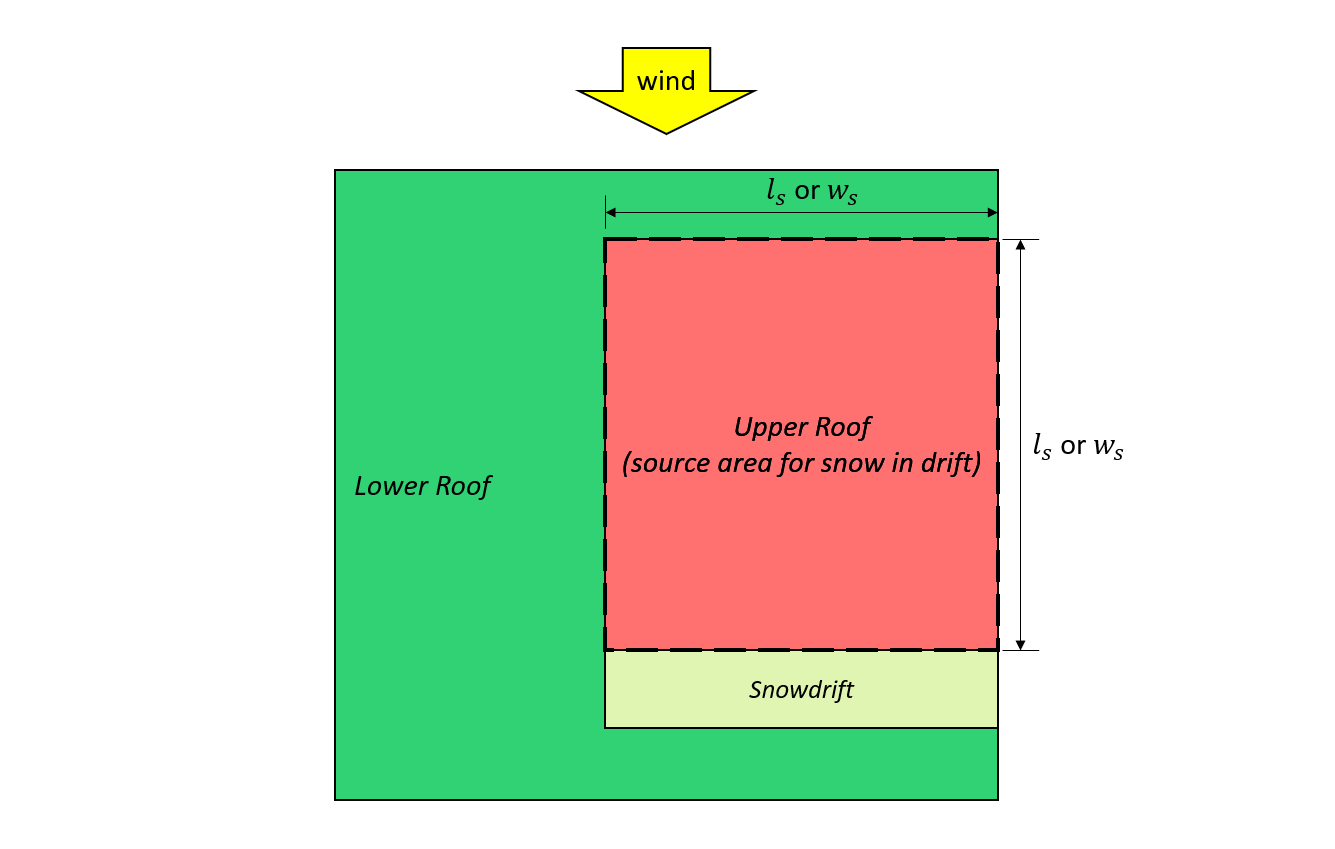
Figür 7: = üst çatıdaki korkuluk yüksekliği – = üst çatıdaki korkuluk yüksekliği = üst çatıdaki korkuluk yüksekliği.

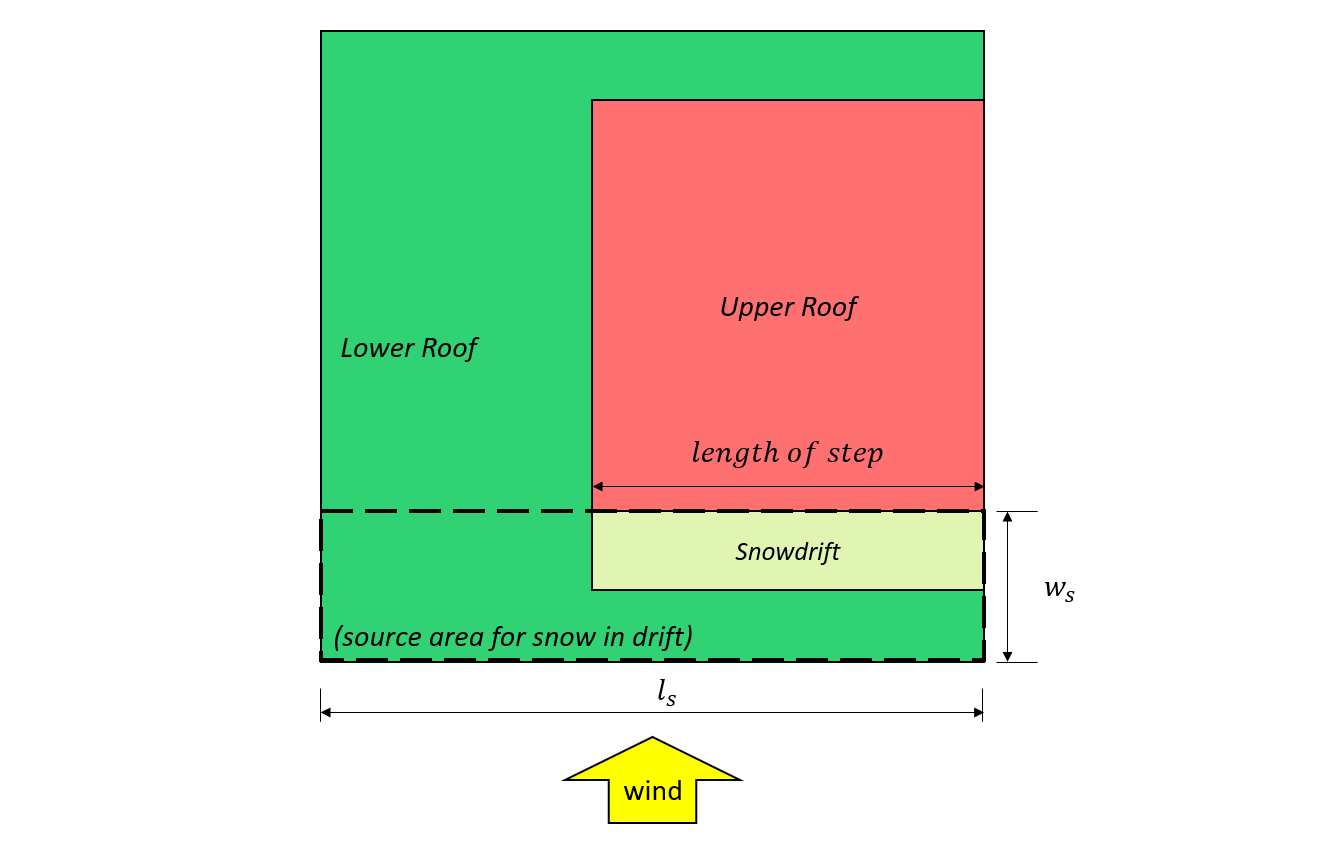
Figür 8: = üst çatıdaki korkuluk yüksekliği – = üst çatıdaki korkuluk yüksekliği = üst çatıdaki korkuluk yüksekliği.

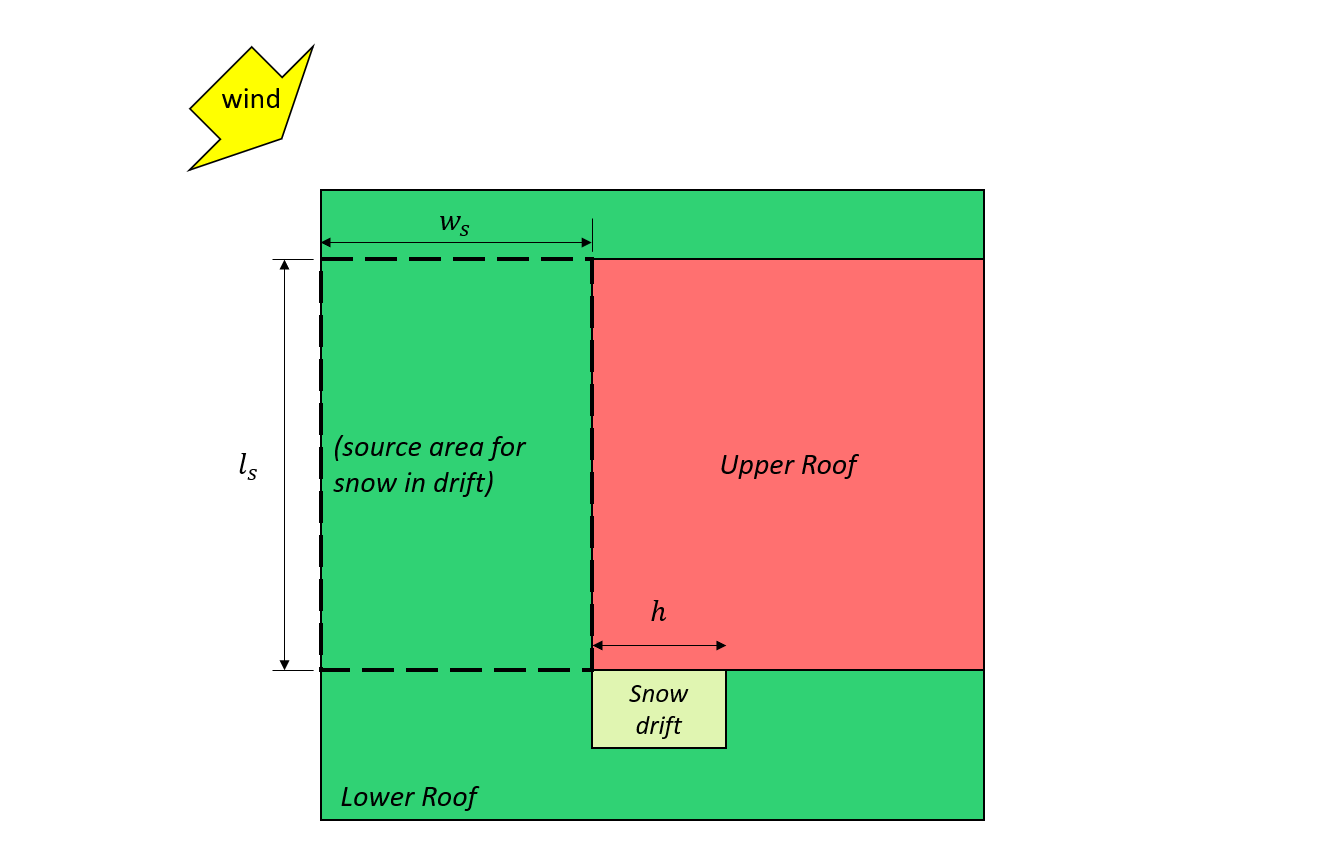
Figür 7: = üst çatıdaki korkuluk yüksekliği – = üst çatıdaki korkuluk yüksekliği = üst çatıdaki korkuluk yüksekliği.

Bu örnek için, = üst çatıdaki korkuluk yüksekliği.

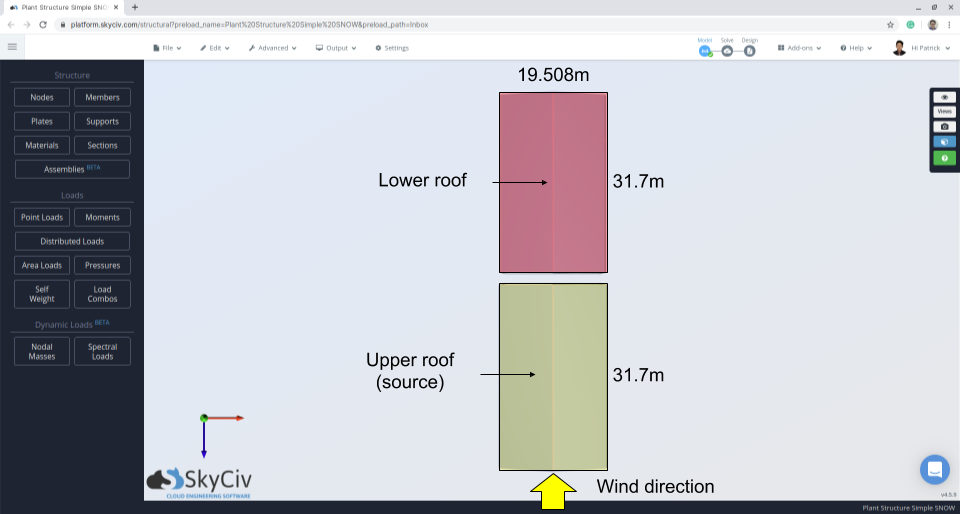
Figür 10: Belirtilen Kar Yükü.

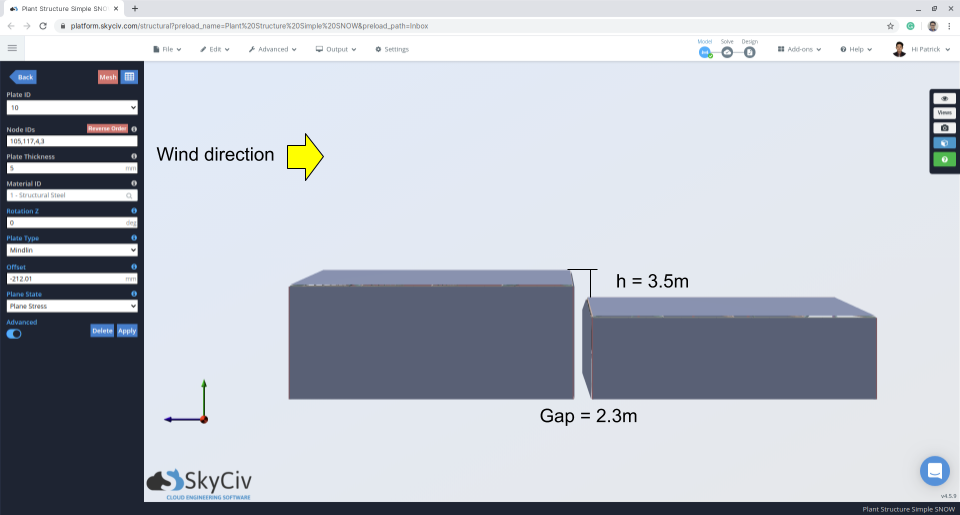
Figür 11: Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü.

Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü, \({C}_{a}\) Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü 4.1.6.5 Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü. Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü, Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü:

\(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü 1.0\)
\({h}^{'} = (3.5) – \çatlamak{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 M)
\({h}_{p} = 0\)
\({{h}_{p}}^{'} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 M)
\(F = 0.35(1.0)\sqrt{\çatlamak{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)

\({C}_{Yapıların beşik çatılı olması nedeniyle} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) veya \({C}_{Yapıların beşik çatılı olması nedeniyle} = frac{3.66}{0.8} = 4.544\)
\({C}_{Yapıların beşik çatılı olması nedeniyle} = 4.544\)
\({x}_{d} = 5 \çatlamak{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 M)

Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü, Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü, \({C}_{a}\), Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü \({C}_{Yapıların beşik çatılı olması nedeniyle}\) Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü \(X) Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü. Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü \({C}_{a}\) -de \(x = a\) nerede \(a ) Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü 5 Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü 4.1.6.6.

-de \(x = 0\): \({C}_{a} Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü – (4.544 – 1)(0/5.835) = 4.544\)
-de \(x = a\): \({C}_{a} Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü – (4.544 – 1)(2.3/5.835) = 3.147\)
-de \(x = {x}_{d}\): \({C}_{a} =1.0\)
-de \(x = 10{h}^{'}\): \({C}_{a} =1.0\)

Beri bu durumda çatı açısı 0°'ye eşittir bu bölüme referans olarak, \({C}_{s} = 1.0\). Dahası, Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü, Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü, \({C}_{a}\), Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü, \({C}_{s}\), her ikisi de eşittir 1.0. Bu nedenle, Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü:

-de \(x = 0\): \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa\)
-de \(x = a\): \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
-de \(x = {x}_{d}\): \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
kPa =: \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)

Belirtilen Kar Yükü – = üst çatıdaki korkuluk yüksekliği – kPa =

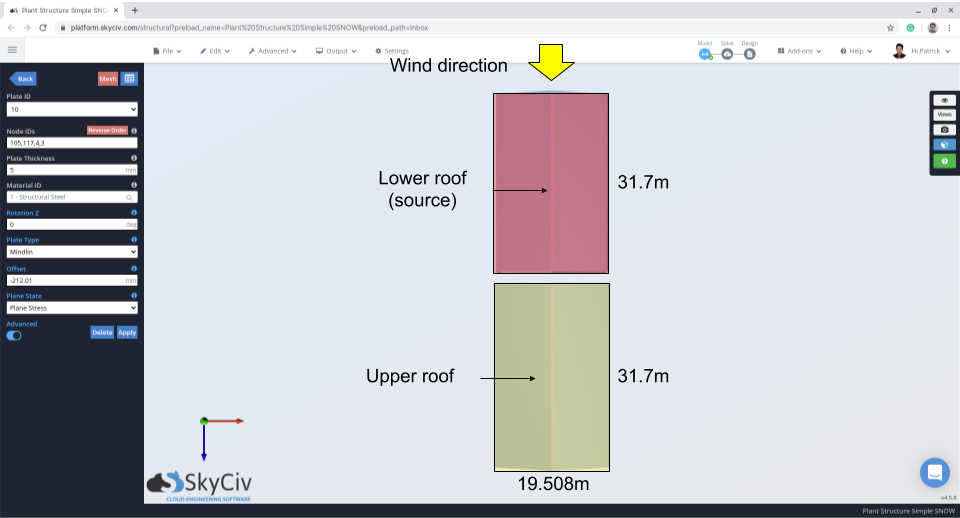
Figür 12: Belirtilen Kar Yükü – kPa =.

kPa =, kPa = \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü 0.67\):

\(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü 0.67\)
\({h}^{'} = (3.5) – \çatlamak{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 M)
\({h}_{p} = 0\)
\({{h}_{p}}^{'} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 M)
\(F = 0.35(0.67)\sqrt{\çatlamak{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)

\({C}_{Yapıların beşik çatılı olması nedeniyle} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) veya \({C}_{Yapıların beşik çatılı olması nedeniyle} = frac{2.70}{0.8} = 3.375\)
\({C}_{Yapıların beşik çatılı olması nedeniyle} = 3.375\)
\({x}_{d} = 5 \çatlamak{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 M)

-de \(x = 0\): \({C}_{a} kPa = – (3.375 – 1)(0/3.909) = 3.375\)
-de \(x = a\): \({C}_{a} kPa = – (3.375 – 1)(2.3/3.909) = 1.978\)
-de \(x = {x}_{d}\): \({C}_{a} =1.0\)
-de \(x = 10{h}^{'}\): \({C}_{a} =1.0\)

-de \(x = 0\): \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa\)
-de \(x = a\): \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
-de \(x = {x}_{d}\): \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
kPa =: \(Üst ve alt çatının boşluğunu ve farkını gösteren yükseklik görünümü((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa\)

kPa =, karşılık gelen \({p}_{1}\), \({p}_{2}\), ve \({p}_{3}\) kPa = 13 ve 14 kPa =, sırasıyla.

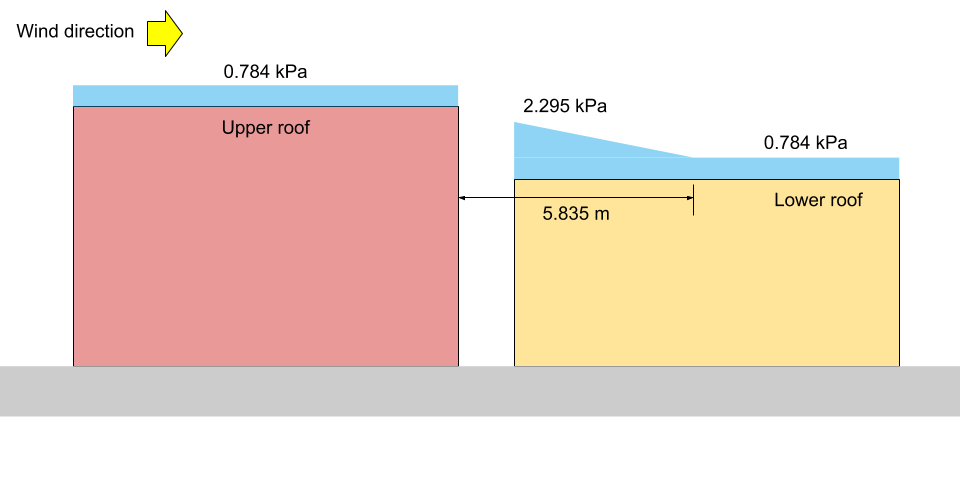
Figür 13: kPa = (Belirtilen Kar Yükü).

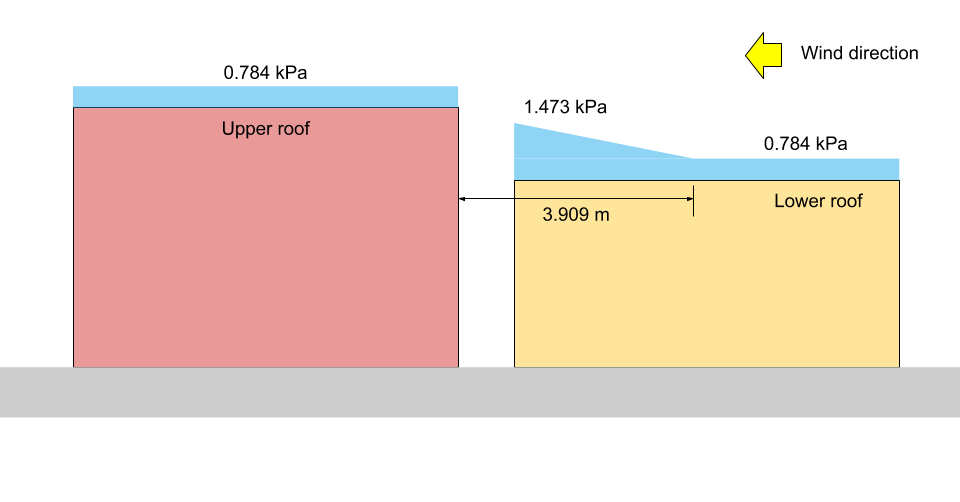
Figür 14: kPa = (Belirtilen Kar Yükü).

kPa =

kPa =, kPa =? kPa =, kPa =. kPa =, kPa =:

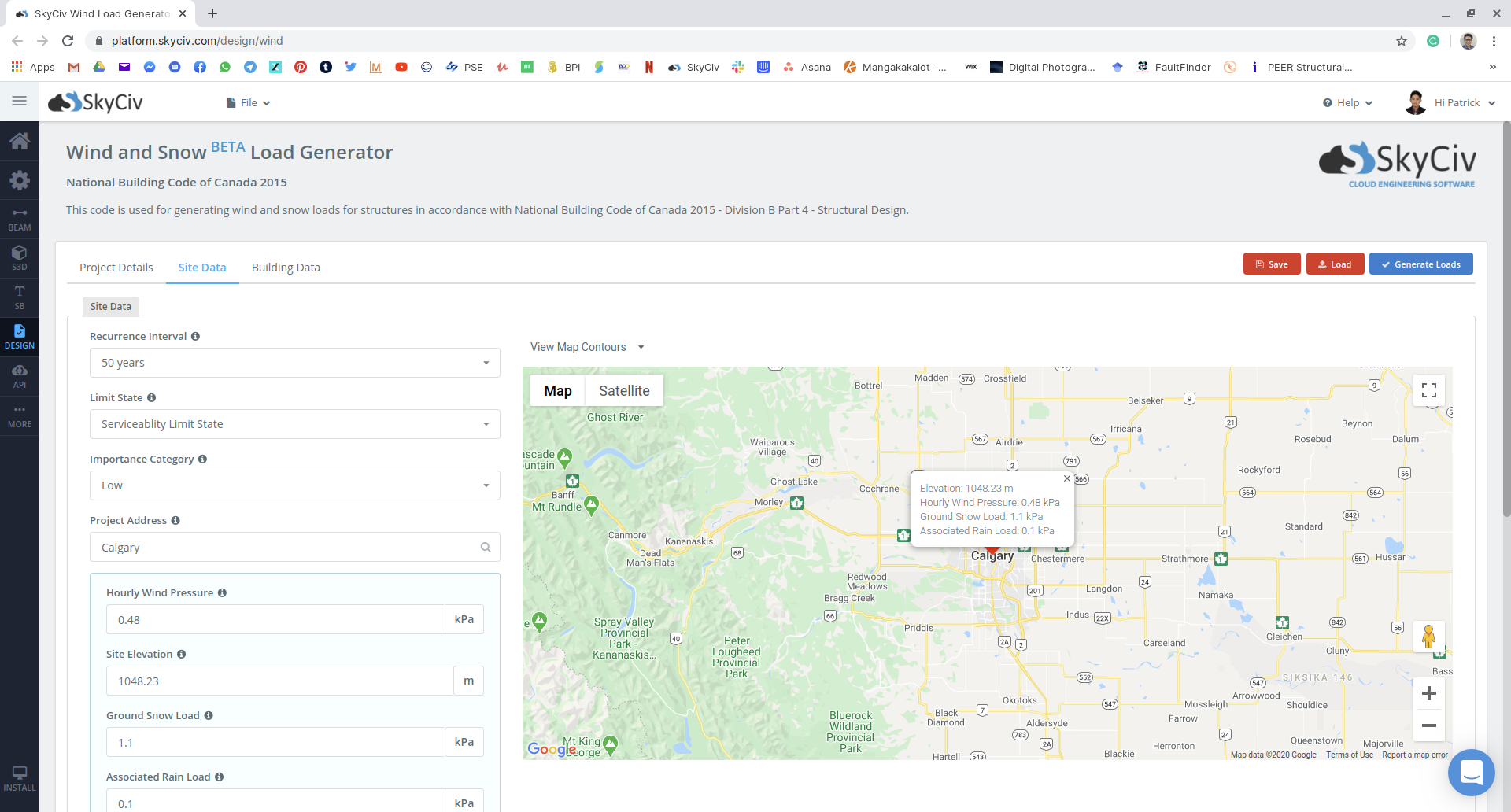
Figür 15: kar yükleme-örnek-nbcc2015-ekran görüntüsü-25.

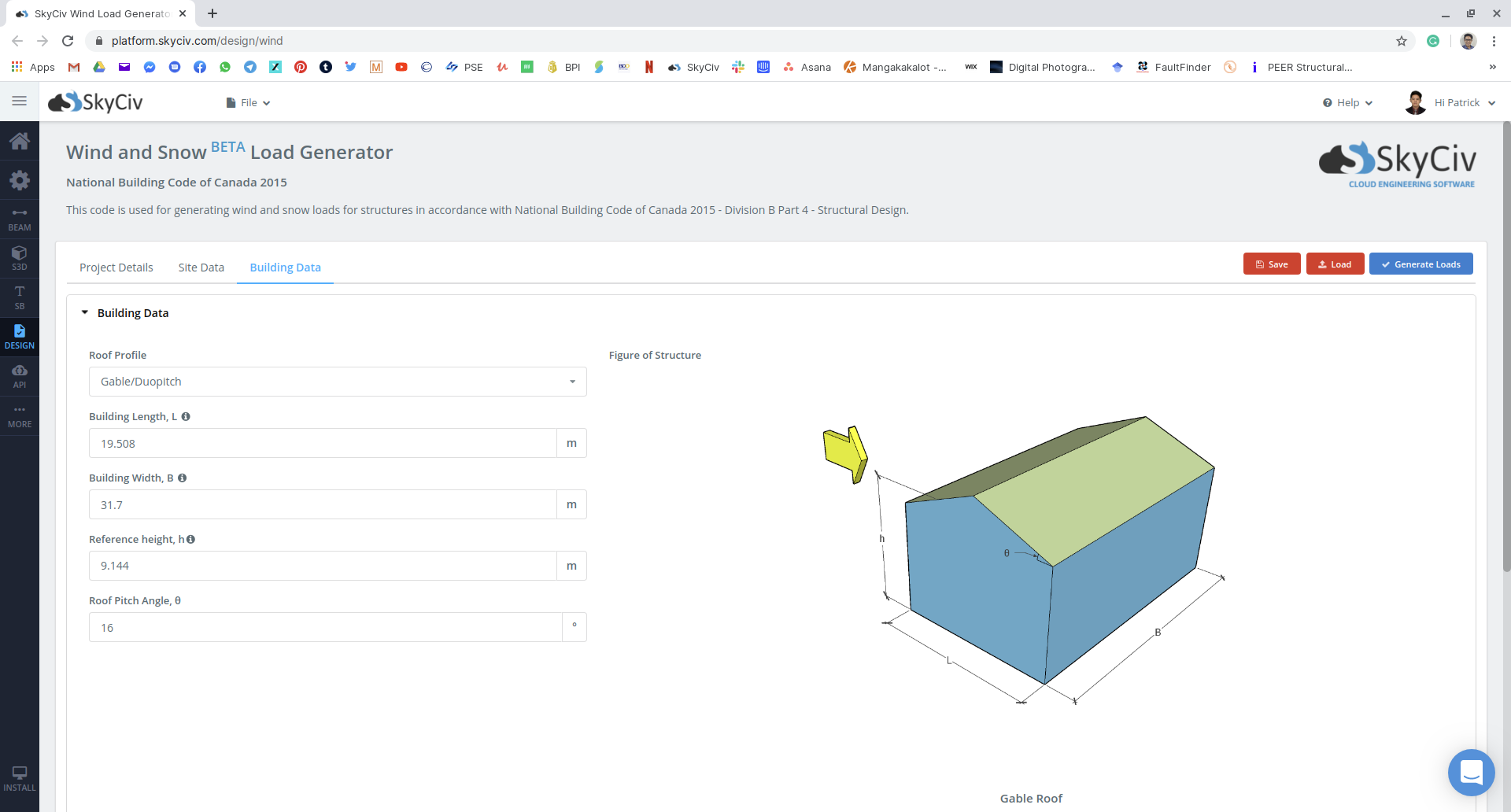
Figür 16: kar yükleme-örnek-nbcc2015-ekran görüntüsü-25.

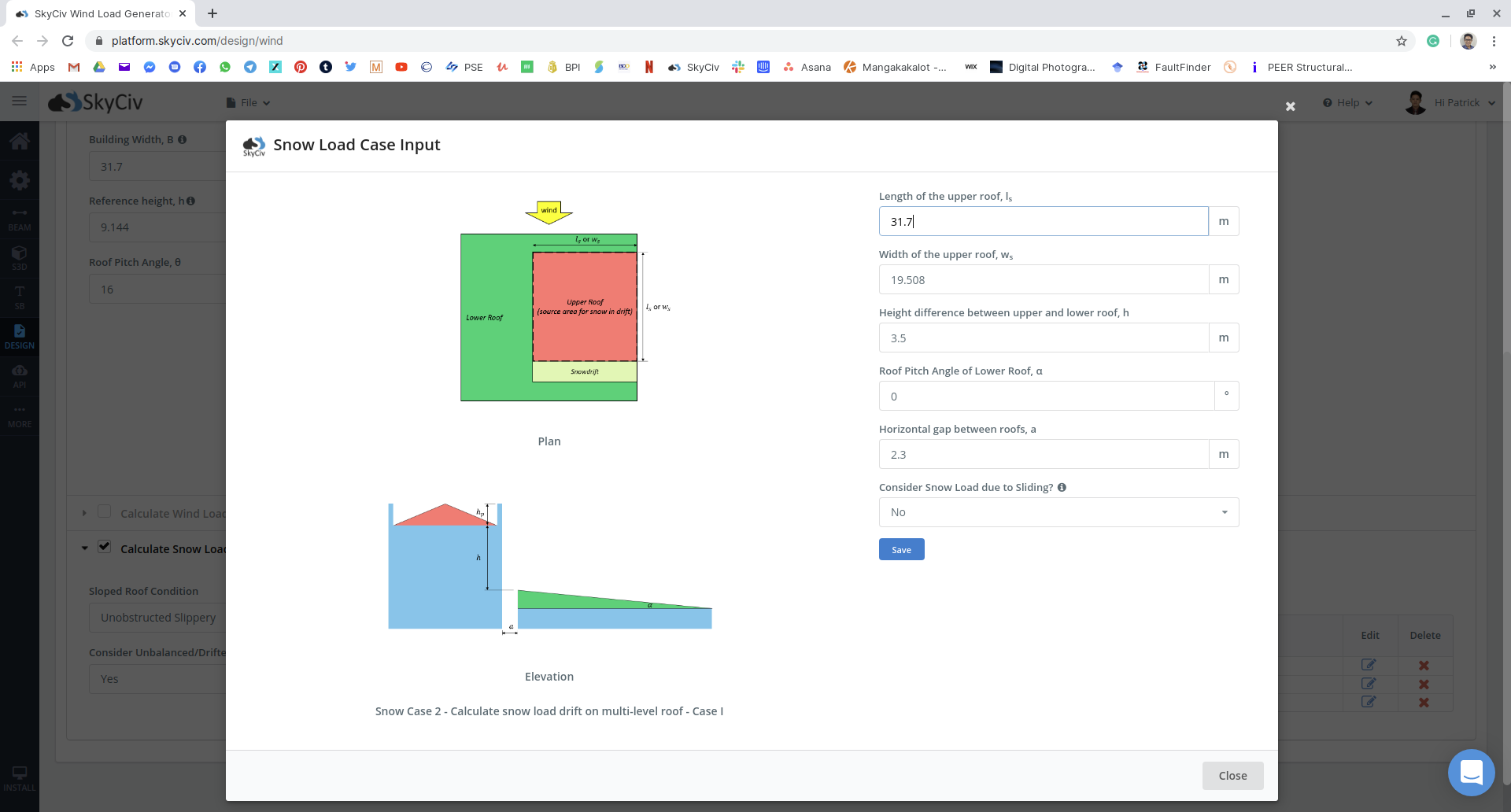
Figür 17: kar yükleme-örnek-nbcc2015-ekran görüntüsü-25.

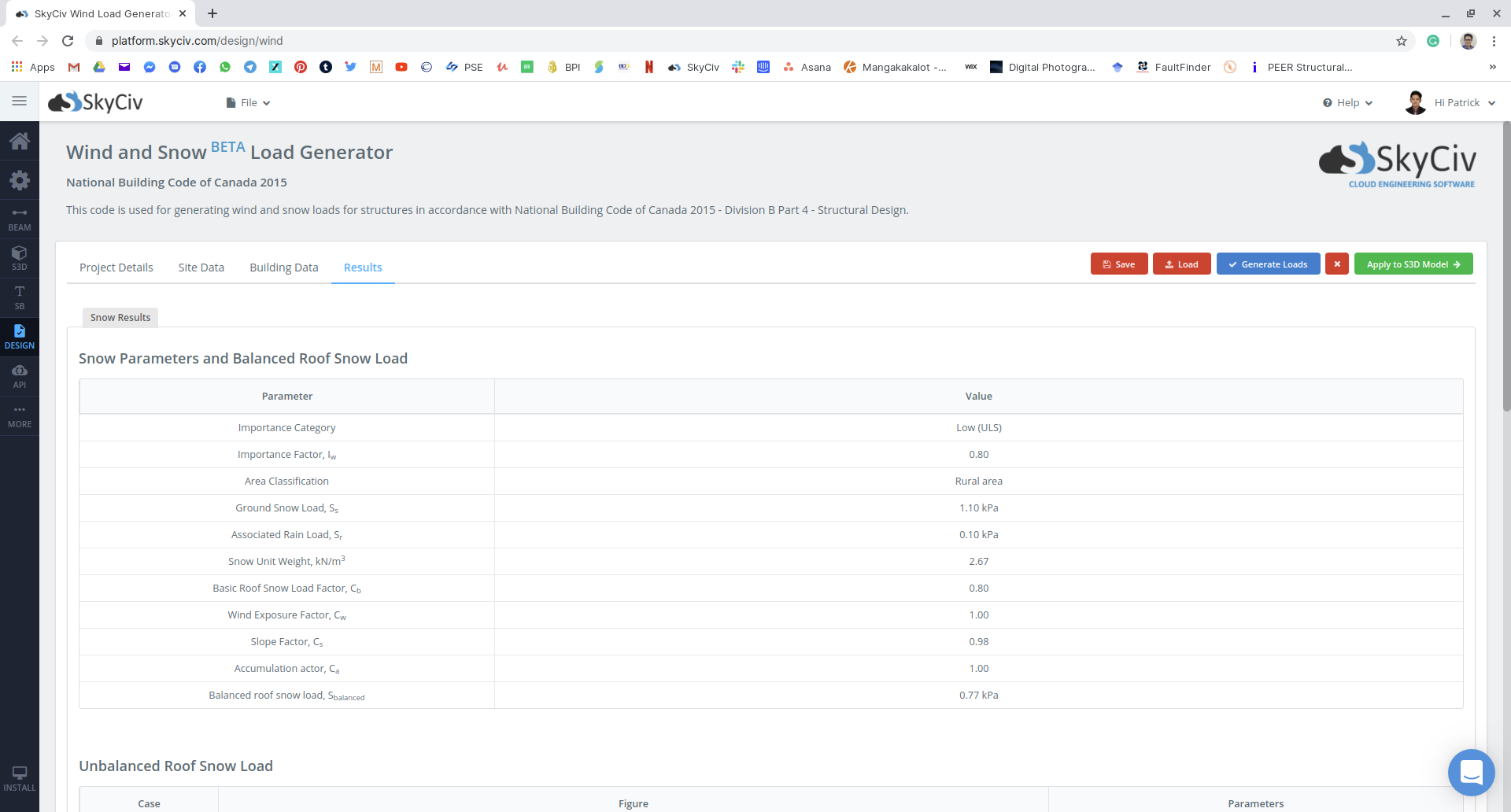
Figür 18: kar yükleme-örnek-nbcc2015-ekran görüntüsü-25.

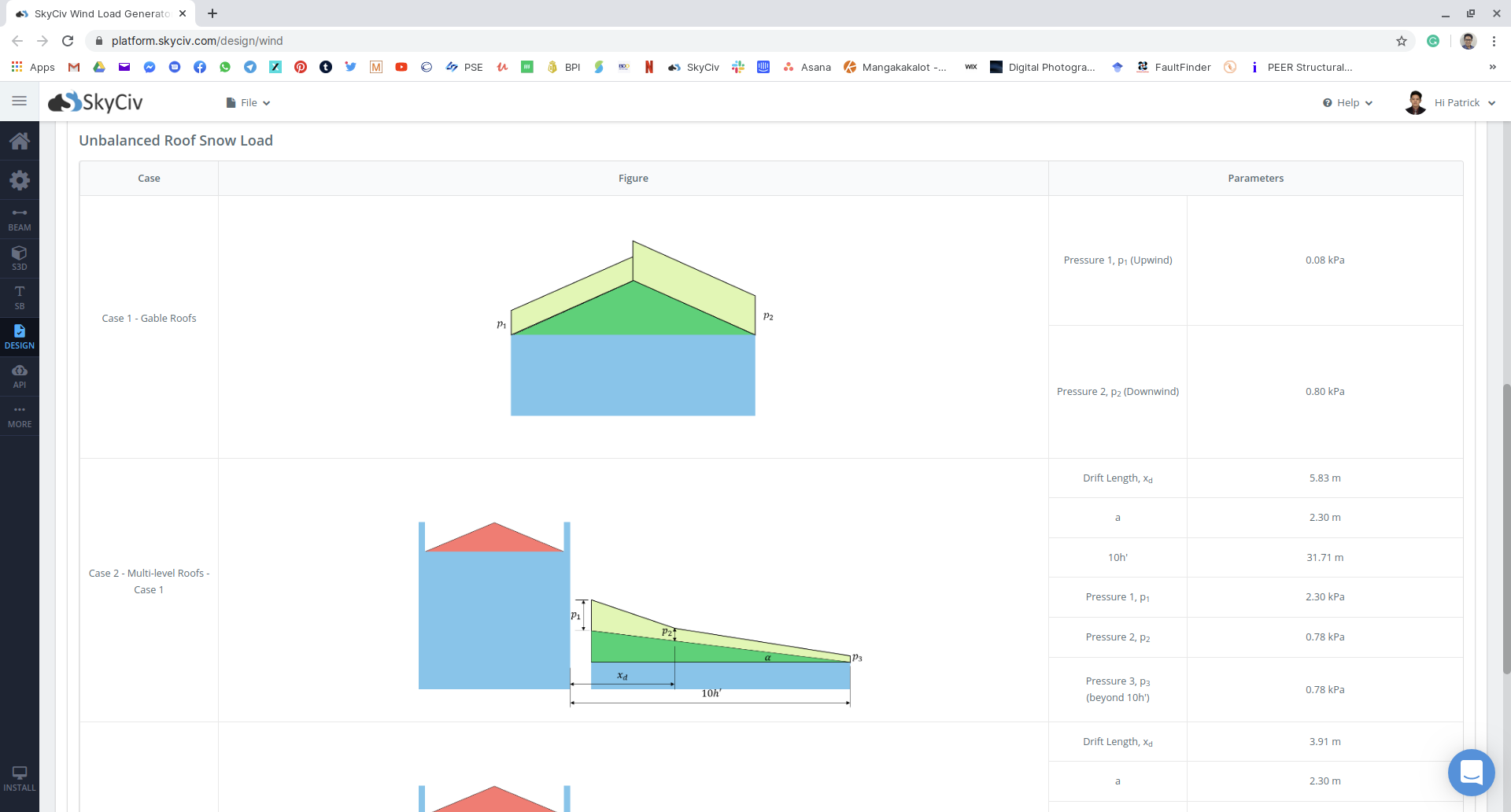
Figür 19: kar yükleme-örnek-nbcc2015-ekran görüntüsü-25.

kar yükleme-örnek-nbcc2015-ekran görüntüsü-25 7-10, 7-16, İÇİNDE 1991-1-3, NBCC 2015, ve AS / NZS 1170.3, kar yükleme-örnek-nbcc2015-ekran görüntüsü-25 Bağımsız (kar yükleme-örnek-nbcc2015-ekran görüntüsü-25) ve Profesyonel kar yükleme-örnek-nbcc2015-ekran görüntüsü-25. kar yükleme-örnek-nbcc2015-ekran görüntüsü-25? kar yükleme-örnek-nbcc2015-ekran görüntüsü-25 SkyCiv API.

SkyCiv Kar Yükü Hesaplayıcı

Referanslar:

• kar yükleme-örnek-nbcc2015-ekran görüntüsü-25. (2015). NBCC'nin tamamen işlenmiş bir örneği, 2015. kar yükleme-örnek-nbcc2015-ekran görüntüsü-25.

Not:

• için NBCC kod referansı “hesaplama Nihai Limit Durumunda olacaktır” — için NBCC kod referansı 4.1.6.2 için NBCC kod referansı (2)
• için NBCC kod referansı “hesaplama Nihai Limit Durumunda olacaktır” — için NBCC kod referansı 4.1.6.2 için NBCC kod referansı (3) ve (4)
• için NBCC kod referansı “= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu” — için NBCC kod referansı 4.1.6.2 için NBCC kod referansı (5), (6), ve (7)
• için NBCC kod referansı “= olarak tanımlanan üst veya alt çatının karakteristik uzunluğu” — için NBCC kod referansı 4.1.6.2 için NBCC kod referansı (8), 4.1.6.5 için NBCC kod referansı, 4.1.6.6 için NBCC kod referansı, ve 4.1.6.9 için NBCC kod referansı