Devrilme Momenti Hesaplama Örneği – Betonarme Konsol
Bu, örneklerle bir istinat duvarında devrilme momentinin nasıl hesaplanacağına dair basit bir kılavuzdur.. Konsollu Beton İstinat Duvarı için yapılan ilk stabilite kontrolü devrilmeye karşıdır.. Devrilme kuvvetlerinin hareketi için, direnen kuvvetlerin, tabanın en alt sol köşesine göre duvarın dönmesini engelleme kapasitesini ifade eder.. Bu iki yük grubu (direnmek ve devirmek) aşağıdaki gibi bölünür:
Dirençli yükler:
- İstinat duvarının kendi ağırlığı
- Topuk ağırlığı üzerinde aktif toprak
- ek yük
devrilme yükler:
- Aktif toprak yanal basıncı
- Ek ücretin varlığından kaynaklanan yanal basınç
Bahsedilen, hesaplama işlemi aşağıda ayrıntılı olarak açıklanacaktır:
Giriş verileri:
Kök
- Yükseklik: 3.124 m
- Genişlik: 0.305 m
- Telafi etmek: 0.686 m
Temel
- Genişlik: 2.210 m
- Kalınlık: 0.381 m
Aktif ve Pasif Toprak
- Ağırlık birimi: 18.85 kN / m3
- Sürtünme Açısı: 35 derece
Alt yapı toprağı
- Ağırlık birimi: 18.85 kN / m3
- Sürtünme Açısı: 35 derece
- Zemin-Beton Sürtünme Katsayısı: 0.55
- İzin verilen yatak basıncı: 143.641 kPa
Toprak Katmanları:
- Aktif: 3.505 m
- Pasif: 0.975 m
- alt yapı: 0.792 m
Ek Yük Değeri: -17.237 kN / m
Dikey yükler:
Beton konsol istinat duvarının maruz kaldığı tüm düşey yükler aşağıdaki resimde gösterilmiştir.:
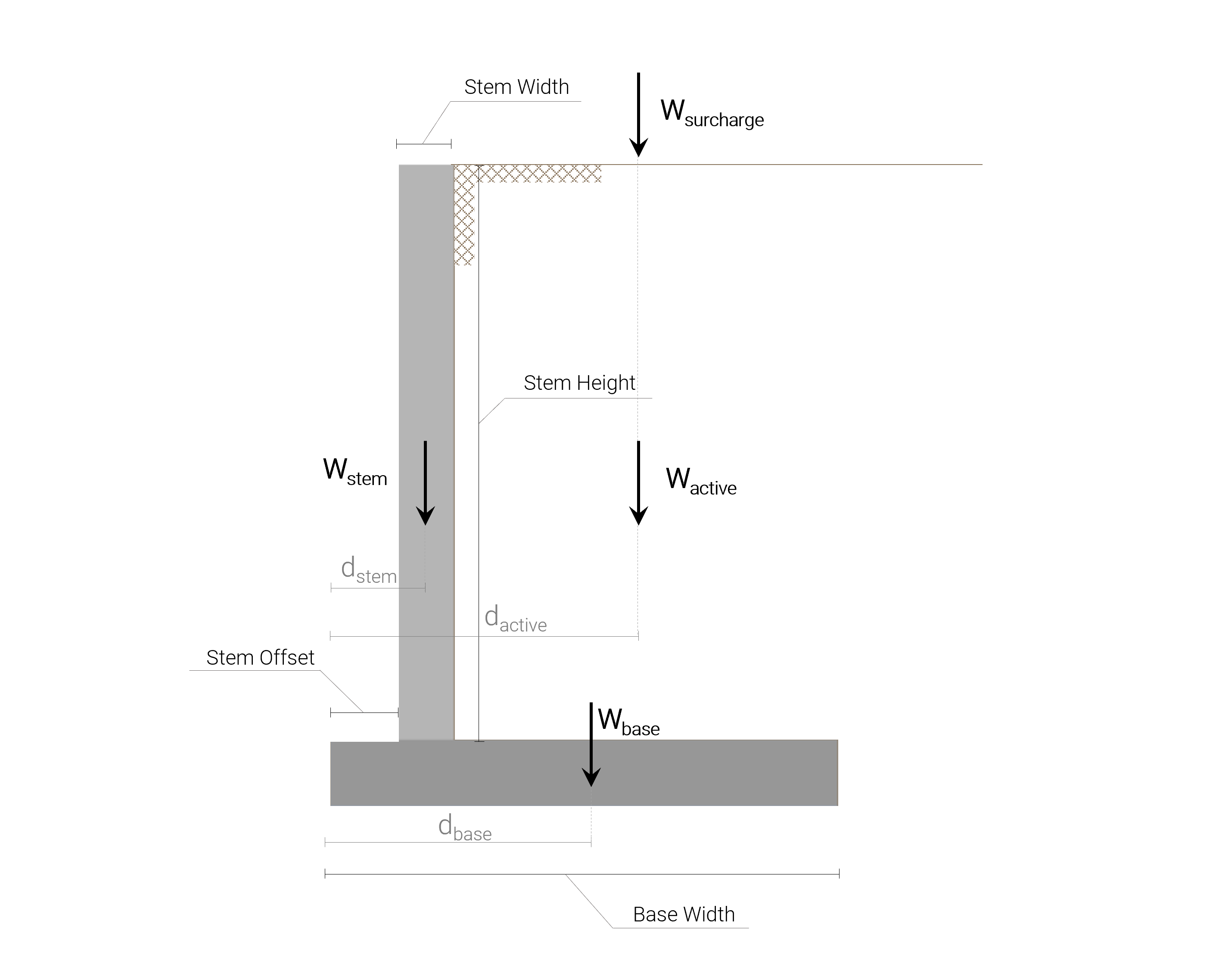
burada belirtmekte fayda var, bu ağırlık (dikey yük) ve pasif zemin kısmı ile ilişkili moment, kaldırılabileceği veya aşınabileceği için ihmal edilir ve bu muhafazakar bir varsayımdır..
\(W_{kök} = \gamma_{Somut} \cdot (kök_{yükseklik} \cdot kök_{Genişlik} ) = 23.58 \;kN/m^3 \cdot 3.124\;m \cdot 0.305\;M)
\( W_{kök}= 22.467\;kN/m\)
\(W_{temel} = \gamma_{Somut} \cdot (temel_{kalınlık} \cdot tabanı_{Genişlik} ) = 23.58 \;kN/m^3 \cdot 0.381\;m \cdot 2.210\;M)
\( W_{temel}= 18.855\;kN/m\)
\(W_{aktif} = \gamma_{toprak,\;aktif} \cdot (kök_{yükseklik}\cdot (temel_{Genişlik}-kök_{telafi etmek}-kök_{Genişlik}) ) \)
\( W_{aktif} = 18.85 \;kN/m^3 \cdot 3.124\;m \cdot (2.210-0.686-0.305)\;M)
\( W_{aktif} = 71.784\;kN/m\)
\(W_{ek ücret} = ek ücret_{değer} \cdot ( (temel_{Genişlik}-kök_{telafi etmek}-kök_{Genişlik} ) \)
\( W_{ek ücret} = 17.237 \;kN/m \cdot (2.210-0.686-0.305)\;M)
\( W_{ek ücret} = 21.012\;kN/m\)
Geri yükleme anı:
Geri yükleme momenti, duvarın tabanın en sol alt köşesine göre dönmesini önlemekle görevlidir.. Bunu hesaplamak için, tüm düşey yüklerin belirtilen noktaya göre bir moment toplamı yapılması gerekmektedir.:
\(M_{kök}=W_{kök}\cdot d_{kök} = 22.467\;kN/m \cdot 0.839\;m=18.839\;kNm/m\)
\(M_{temel}=W_{temel}\cdot d_{temel} = 18.855\;kN/m \cdot 1.105\;m=21.939\;kNm/m\)
\(M_{aktif}=W_{aktif}\cdot d_{aktif} = 71.784\;kN/m \cdot 1.601\;m=114.89\;kNm/m\)
\(M_{ek ücret}=W_{ek ücret}\cdot d_{ek ücret} = 21.012\;kN/m \cdot 1.601\;m=33.630\;kNm/m\)
\( \Sigma{M_{R}} = M_{kök}+M_{temel}+M_{aktif}+M_{ek ücret}\)
\( \Sigma{M_{R}} = 18.839+21.939+114.89+33.630\)
\( \Sigma{M_{R}} = 189.298\;kNm/m\)
yatay yükler:
Beton konsol istinat duvarının maruz kaldığı tüm yatay yükler aşağıdaki resimde gösterilmiştir.:
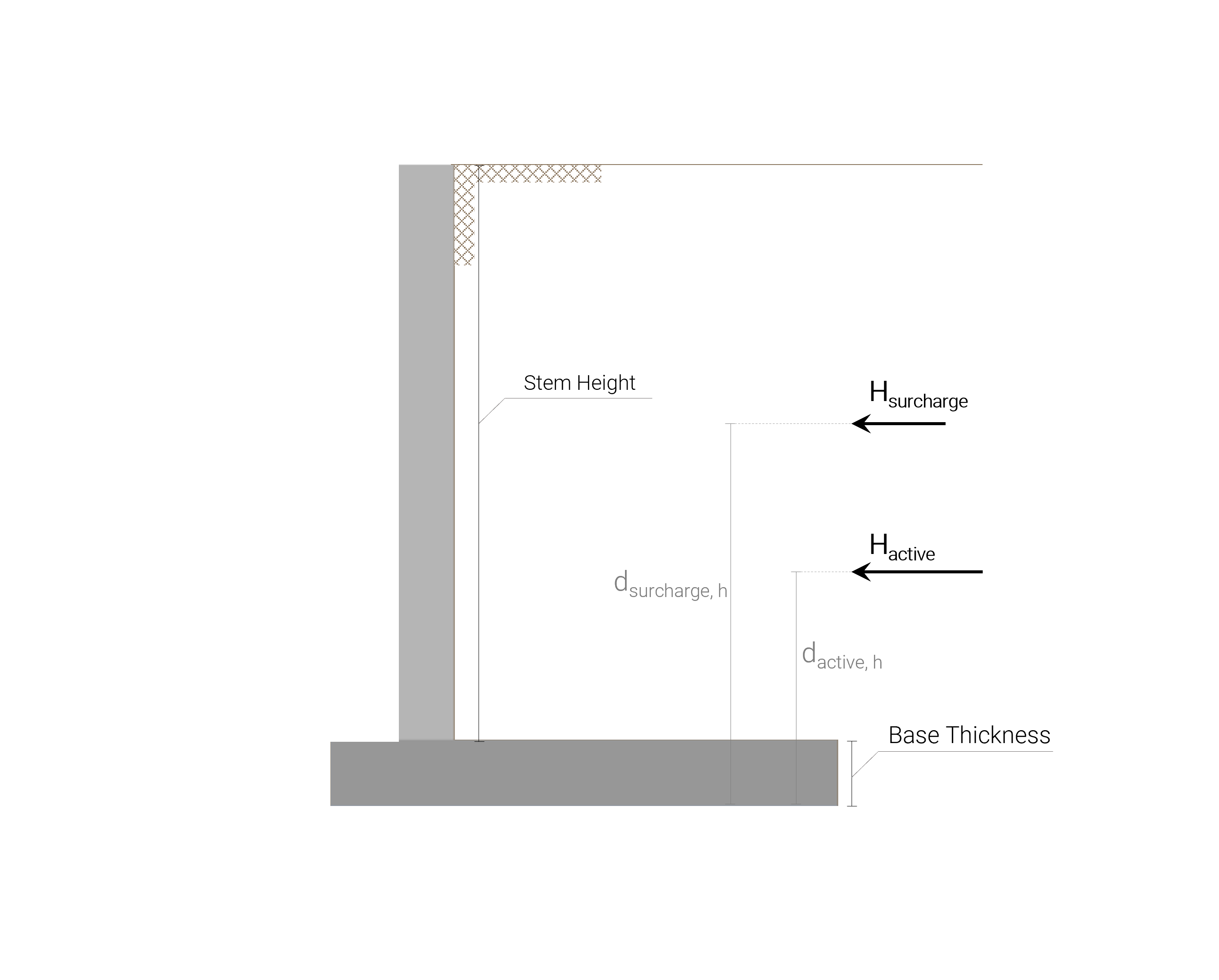
Tutulan toprak aktif basıncından kaynaklanan yanal toprak basıncını ve ek yük sonucu yanal basıncı hesaplamak için, Rankine aktif toprak basıncı katsayısını hesaplamak gerekir:
\( [object Window]{1-\olmadan(\gama_{toprak,\;aktif})}{1+\olmadan(\gama_{toprak,\;aktif})} \)
\( [object Window]{1-\olmadan(35º)}{1+\olmadan(35º)} = 0.271 \)
Bu sonuçla, artık tutulan zeminin uyguladığı yanal aktif basınçtan kaynaklanan yatay yükü hesaplamak mümkündür.:
\(H_{aktif} = frac{1}{2} \[object Window]{toprak,\;aktif} \cdot (kök_{yükseklik} + temel_{kalınlık})^{2} \cdot K_a \)
\(H_{aktif} = frac{1}{2} \cdot 18.85\;[object Window]{2} \cdot 0.271 \)
\(H_{aktif} = 31.377\;kN / m \)
Sürşarj mevcudiyeti ile ilgili yatay kuvveti hesaplamak için, önce eşdeğer bir toprak yüksekliği hesaplanır, ve sonra gerçek güç:
\( h_{toprak,\;eşdeğer} = frac{ek ücret_{değer}}{\gama_{toprak,\;aktif}} = frac{17.237 \;= gama_{2}}{18.85 \;= gama_{3}} \)
\( h_{toprak,\;eşdeğer} = 0.914 \; m \)
\( H_{ek ücret} [object Window]{toprak,\;aktif} \cdot h_{toprak,\;eşdeğer} \cdot (kök_{yükseklik} + temel_{kalınlık}) \[object Window])
\(H_{ek ücret} =\cdot 18.85\;kN/m^3 \cdot 0.914 \; m \cdot 3.505 \; m \cdot 0.271 \)
\(H_{ek ücret} = 16.372\;kN / m \)
devrilme anı
Devrilme momenti, tabanın en sol alt köşesine göre yatay yüklerin oluşturduğu moment olarak hesaplanır.. Yatay yüklerin her biri için kaldıraç mesafesi:
- Duvarın tabanın altından yüksekliğinin üçte biri için tutulan toprağın aktif basınç dağılımının sonucu. Bu basınç, yüzey seviyesinde sıfır değeri ve taban seviyesinin altında maksimum değeri olan üçgen bir dağılım izlediği için böyledir..
- Bu durumda, duvarın tabanın tabanından yüksekliğinin yarısı ek yükün varlığından kaynaklanan yatay yük. Bu basınç dikdörtgen bir dağılım izlediği için böyledir..
Bahsedilen, devrilme momenti aşağıdaki gibi hesaplanır:
\( M_{aktif} = H_{aktif} \cdot \frac{1}{3} \; (kök_{yükseklik} + temel_{kalınlık}) \)
\( M_{aktif} = 31.377\;kN/m \cdot \frac{1}{3} \; 3.505\;m \)
\( M_{aktif} = 36.659 \;kNm/m \)
\( M_{ek ücret, \;h} = H_{ek ücret} \cdot \frac{1}{2} \; (kök_{yükseklik} + temel_{kalınlık}) \)
\( M_{ek ücret, \;h} = 16.372\;kN/m \cdot \frac{1}{2} \; 3.505\;m \)
\( M_{ek ücret, \;h} = 28.692\;kNm/m \)
\( \Sigma{M_{OTM}} = M_{aktif}+M_{ek ücret, \;h}\)
\( \Sigma{M_{OTM}} = 36.659 \;kNm/m+28.692\;kNm/m\)
\( \Sigma{M_{OTM}} = 65.351\;kNm/m\)
Devrilmeye karşı Güvenlik Faktörü
ACI 318 bir güvenlik faktörünün daha büyük veya buna eşit olmasını önerir. \(2.0\). aşağıdaki gibi hesaplanır:
\( [object Window]{\Sigma{M_{R}}}{\Sigma{M_{OTM}}} \)
\( [object Window]{189.298\;kN\ast m}{65.351\;kN\ast m}= 2.897 \vermek 2.0\) GEÇMEK!
İstinat Duvarı Hesaplayıcı
Bu makalede, devrilme momenti hesaplama örneklerini tartıştık. SkyCiv, devrilme momentini kontrol edecek ve istinat duvarlarınızda stabilite analizi yapacak ücretsiz bir İstinat Duvarı Hesaplayıcısı sunar.. Ücretli sürüm ayrıca tüm hesaplamaları görüntüler., böylece istinat duvarının devrilmeye karşı stabilitesinin nasıl hesaplanacağını adım adım görebilirsiniz, sürgülü ve yatak!
Ürün geliştirici
BEng (Sivil)



