Temel, yapının toplam yüklerini zemine ileterek ve dağıtarak genel stabiliteyi sağlamak için bir yapının önemli bir unsurudur.. sığ temeller, dikdörtgen veya kare izole temel gibi, derin temellere kıyasla inşaatlarının basitliği ve toplam maliyeti nedeniyle tercih edilen temel türüdür.. Taban basıncını tahmin etmek, temelin tasarımını ve boyutunu önemli ölçüde etkiler. Tipik, Zeminin izin verilen taşıma kapasitesi ile temel altındaki geçerli taban basıncı arasındaki fayda oranı, temelin başlangıç ​​boyutunun temelidir.. İlk temel boyutları ayarlandıktan sonra, güvenlik ve stabilite için daha fazla tasarım kontrolleri, tek yönlü ve iki yönlü kesme gibi, bükme kapasitesi, ve geliştirme uzunluğu kontrolleri, hangi tasarım kodunun kullanıldığına bağlı olarak kontrol edilir.

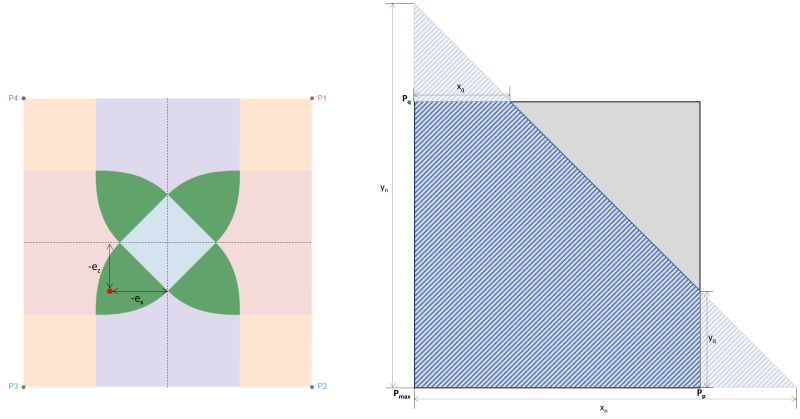
Bir temel çift eksenli bir eğilmeye maruz kaldığında (M_x, M_ile), eksenel yükün olduğu varsayılır (P) bir eksantriklik koordinatı üzerinde hareket ediyor (e_x, e_ile) merkezden dönme eğiliminin olduğu yerde. Zemin ve temel arasındaki etkileşim temel olarak temel boyutuna ve uygulanan yüklerin ortaya çıkan eksantrikliğine bağlıdır.. Ortaya çıkan eksantrikliğin konumuna bağlı olarak, taban basıncı, temelin tam veya kısmi sıkıştırmada olmasına neden olur. Uygulamada, tam sıkıştırmada bir temel tasarlamanız önerilir. Zemin ile temel arasındaki kısmi sıkışma veya temas kaybı ihmal edilmemelidir., ancak çoğu tasarımcı, hesaplama karmaşıklığı nedeniyle bu senaryodan kaçınır.. Ortaya çıkan eksantriklik karakter aralığı içinde veya Bölge C'nin altında olduğunda, temel tam sıkıştırmadadır.. Bölge C'nin dışındaki eksantriklik, temeli kısmi sıkıştırmaya sokar. Figür 1 dikdörtgen bir temel üzerinde farklı belirlenmiş bölgeleri gösterir.

Bu makale, Bellos'a dayalı farklı bölge sınıflandırmaları altında köşe basınçlarının hesaplanmasına odaklanacaktır. & İz (2017) ve SS. Ray'in (1995) çalışmalar.

Dikdörtgen bir temelin bölge sınıflandırmaları

Dikdörtgen bir temelin bölge sınıflandırmaları, farklı yazarlar tarafından, beklenen yükleme koşulları altında zemin basıncının dağılımını tahmin etmeye yönelik pratik bir yaklaşım geliştirmek için yapılan çok sayıda çalışmadan elde edilmiştir.. Şekilde gösterildiği gibi 1, beş farklı bölge var (Bölgeler A-E) Ortaya çıkan eksantrikliğin konumuna bağlı olarak. Her bölge farklı bir yüklemeye karşılık gelir, baz basınç dağılımı, ve deformasyon. Bölge C, kertenkele olarak da bilinir, ana çekirdek. Temel tasarımı için ideal bölgedir., temel üzerinde tam sıkıştırma ile sonuçlanır. Bu bölgenin boyutları şuna eşittir: 1/6 ilgili temel uzunluğunun.

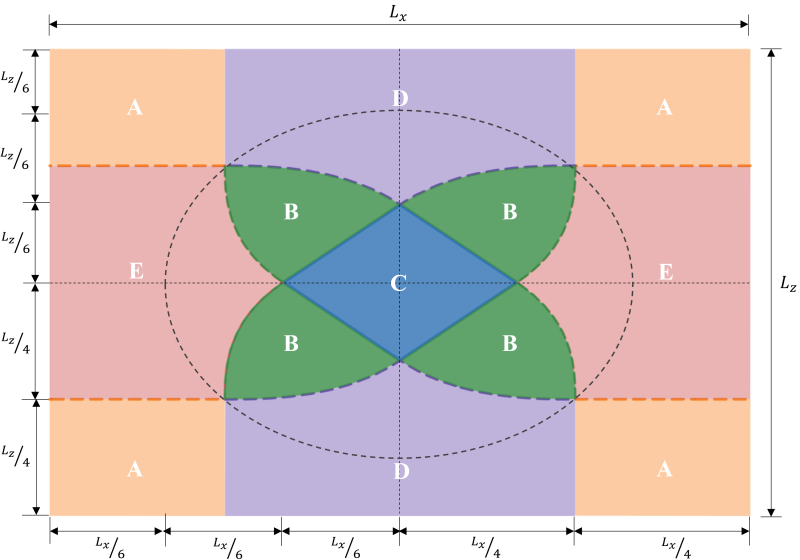
Figür 1: Dikdörtgen bir temelin bölge sınıflandırmaları

 

İkincil çekirdek eliptik alandır (Şekilde kesikli çizgi ile sınırlandırılmıştır 1) majör ve minör yarı eksenleri eşit 1/3 ilgili temel uzunluğunun. Bu bölge tüm B bölgelerini kapsar & C ve D bölgelerinin bazı bölümleri & E. İkincil çekirdek, temelin kısmen sıkıştırılmasına neden olur. Kabul edilebilir bir temel tasarımı için ikincil bölge içindeki eksantrikliği korumak iyi bir uygulamadır..

İkincil bölgenin ötesindeki eksantriklik, yüksek çift eksenli yüklemenin sonucudur. A bölgesinin tamamını ve D bölgelerinin kalan kısımlarını kapsar. & E. Devrilme riski taşıyacağından, temellerin bu bölgelerde tasarlanmasından kaçınılması tavsiye edilir.. Bu nedenle, Bu yükleme türü için temel boyutlarının yeniden tasarlanması tavsiye edilir..

 

Aşağıda, her bölge sınıflandırmasındaki köşe basınçlarını çözmek için analitik formüller sıralanmaktadır..

Bölge C (Ana çekirdek, Tam sıkıştırma bölgesi)

Söylendiği gibi, Bu, temelin tüm tabanını sıkıştırmaya ayarlayabildiğinden, temel tasarımı için en çok tercih edilen durumdur., Şekilde gösterildiği gibi 2. Bu durum, karakter aralığı içinde küçük eksantriklik veya eksantriklik olmaması ile temsil edilir.. Figür 2 P3 köşelerindeki maksimum basıncıyla çekirdek içindeki eksantrikliği gösterir & P4 ve P1 köşelerinde minimum basınç & kilo kaybı hikayeleri.net.

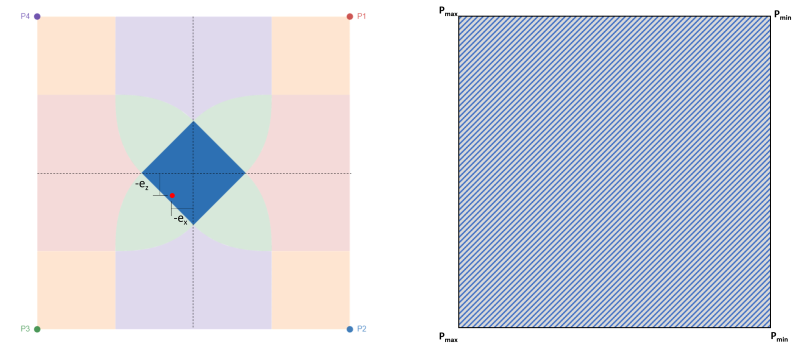
Figür 2: eksantriklik (-e_x, -e_ile) Bölge C'de & tam sıkıştırma alanı

= Etkili kesme derinliği = & minimum köşe basınçları (güzel & İz, 2017):

 

 

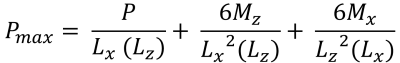
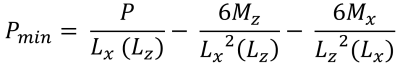
Eksantrikliğe dayalı köşe basınçları
	P1	P2	P3	P4
+ex, +eile	Pmax	Pmax	Pmin	Pmin
+ex, -eile	Pmax	Pmax	Pmin	Pmin
-ex, -eile	Pmin	Pmin	Pmax	Pmax
-ex, +eile	Pmin	Pmin	Pmax	Pmax

Bölge A (Üçgen sıkıştırma bölgesi)

Bu durum, ayağın her köşesinde dört adet dikdörtgen alana karşılık gelmektedir.. Genellikle büyük iki eksenli eksantriklik ile oluşur, köşelerden birinde yüksek üçgensel bir sıkıştırma alanı empoze etmek, Şekilde gölgeli bölge ile gösterildiği gibi 3. Kalan köşeler toprakla temasını kaybeder. Bu nedenle, bu durum tasarım için önerilmez.

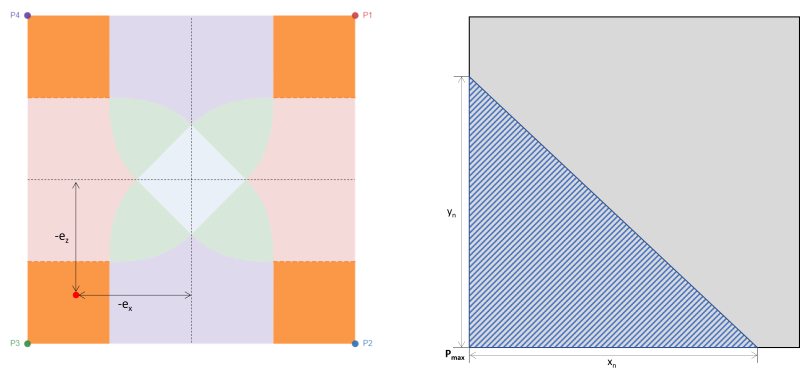Figür 3: eksantriklik (-e_x, -e_ile) Bölge A'da & P3 etrafındaki üçgen sıkıştırma alanı

 

Rulman için önerilen güvenlik faktörü (güzel & İz, 2017):

 

 

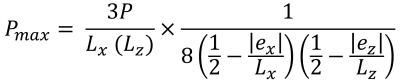
Eksantrikliğe dayalı köşe basınçları
	P1	P2	P3	P4
ex(+), eile(+)	Pmax	0	0	0
ex(+), eile(-)	0	Pmax	0	0
ex(-), eile(-)	0	0	Pmax	0
ex(-), eile(+)	0	0	0	Pmax

Bölge D (Trapez sıkıştırma bölgesi)

Bölge D ayrıca temelin x yönündeki alanlardaki büyük dışmerkezliklere karşılık gelir., Şekilde gösterildiği gibi 4. z yönündeki eksantriklik (e_ile) x yönünde olduğundan çok daha büyük (e_x). Bu durumda, Temelin iki köşesi toprakla temasını kaybeder ve yamuk şeklinde bir basınç alanı oluşturur.. A bölgesi ile karşılaştırıldığında, tamamen ikincil bölgenin dışında olan, D bölgesinin bir kısmı hala ikincil bölge tarafından kapsanmaktadır..

 

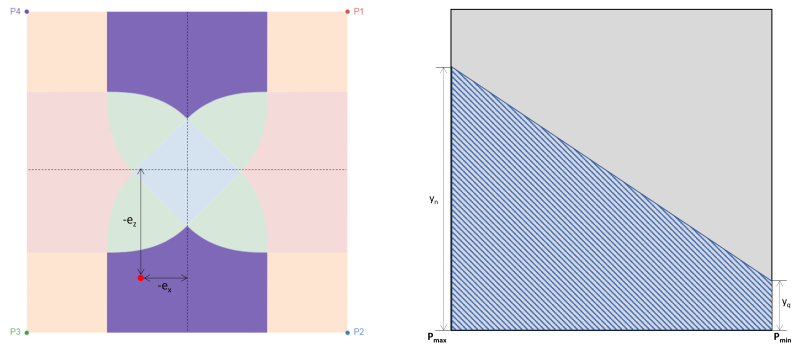
Figür 4: eksantriklik (-e_x, -e_ile) Bölge D'de & P3 etrafındaki yamuk sıkıştırma alanı

 

= Etkili kesme derinliği = & minimum köşe basınçları (güzel & İz, 2017):

 

 

 

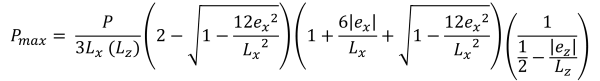
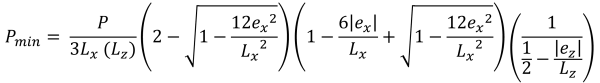
Trapez sıkıştırma alanının dikey yükseklikleri (güzel & İz, 2017):

 

 

 

 

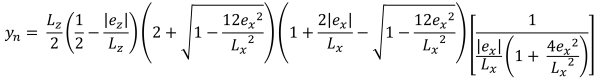
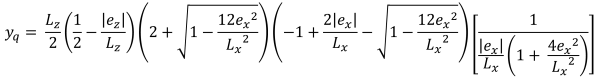
Eksantrikliğe dayalı köşe basınçları
	P1	P2	P3	P4
ex(+), eile(+)	Pmax	0	0	Pmin
ex(+), eile(-)	0	Pmax	Pmin	0
ex(-), eile(-)	0	Pmin	Pmax	0
ex(-), eile(+)	Pmin	0	0	Pmax

 

E Bölgesi (Trapez sıkıştırma bölgesi)

D bölgesine benzer, bu durum aynı zamanda yamuk bir sıkıştırma alanı üretir, ancak x yönündeki büyük bir eksantriklikten kaynaklanır.(e_x).

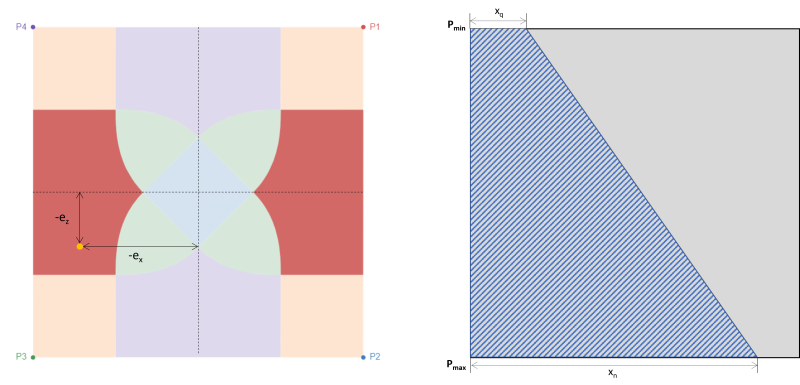Figür 5: eksantriklik (-e_x, -e_ile) Bölge E'de & P3 etrafındaki yamuk sıkıştırma alanı

 

= Etkili kesme derinliği = & minimum köşe basınçları (güzel & İz, 2017):

 

 

 

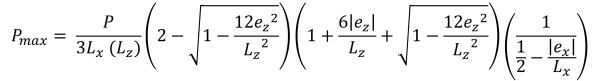
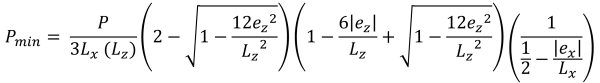
Trapez sıkıştırma alanının yatay tabanları (güzel & İz, 2017):

 

 

 

 

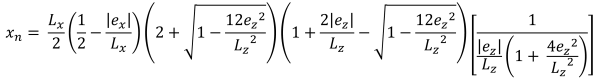
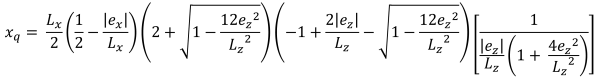
Eksantrikliğe dayalı köşe basınçları
	P1	P2	P3	P4
ex(+), eile(+)	Pmax	Pmin	0	0
ex(+), eile(-)	Pmin	Pmax	0	0
ex(-), eile(-)	0	0	Pmax	Pmin
ex(-), eile(+)	0	0	Pmin	Pmax

Bölge B (Beşgen sıkıştırma bölgesi)

Bu durum, temellere uygulanan yükler ikincil bölge içinde orta derecede bir dışmerkezlik oluşturduğunda meydana gelir.. B bölgesinin kapsadığı alanlar, C bölgesinin dış taraflarını çevreleyen iki eğimli kenar ve bir düz taban ile sınırlanmıştır.. Bu durumda, beşgen bir sıkıştırma alanı üretilir, ve temelin sadece bir köşesi toprakla temasını kaybeder. ancak, Aşağıda verilen çözümler biraz karmaşıktır ve köşe basınçları ve x için sayısal çözüm yöntemleri gerektirir. & sıkıştırma alanının y kesişimleri.

Köşe basınçları (güzel & İz, 2017):

 

 

 

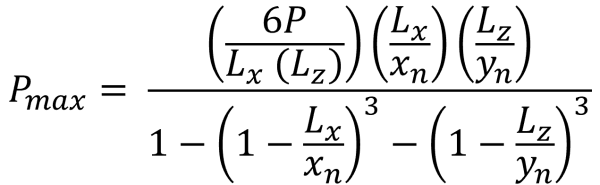
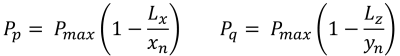
Sıkıştırma alanının beşgen kenarları (güzel & İz, 2017):

 

 

 

 

 

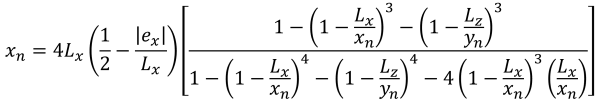
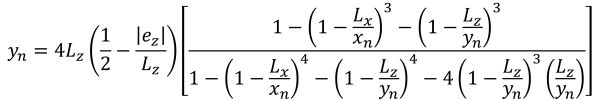
Eksantrikliğe dayalı köşe basınçları
	P1	P2	P3	P4
ex(+), eile(+)	Pmax	Pq	0	Pp
ex(+), eile(-)	Pp	Pmax	Pq	0
ex(-), eile(-)	0	Pp	Pmax	Pq
ex(-), eile(+)	Pq	0	Pp	Pmax

 

Alternatif olarak, S.S. tarafından daha doğrudan bir çözüm. Işın (1995) beşgen sıkıştırma bölgesinin köşe basınçları ve kesişmeleri için kullanılabilir. Denklemler aşağıda verilmiştir:

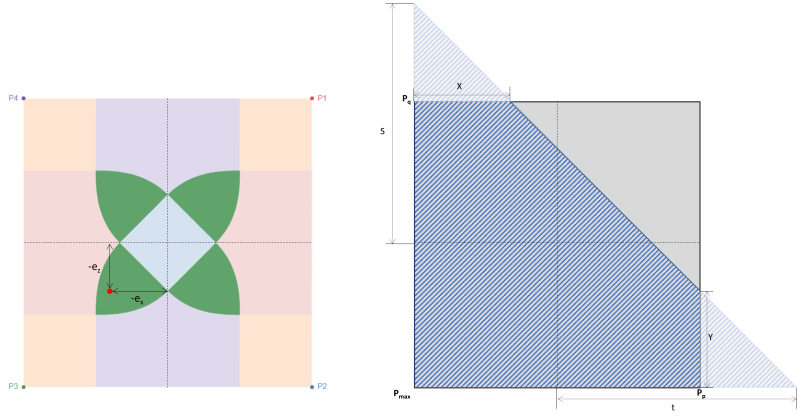
Köşe basınçları (SS. Işın, 1995):

 

 

 

 

Sıkıştırma alanının beşgen kenarları (SS. Işın, 1995):

 

 

---

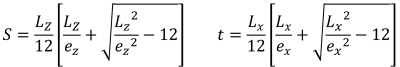
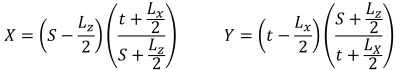
SkyCiv’in Temel Tasarım Modülü Dikdörtgen beton temelin taban basınçlarını çözebilir. Farklı tasarım kodlarına göre ek tasarım kontrolleri (ACI 318-14, Avustralya standardı 2009 & 2018, Eurocode, ve Kanada standartları) ayrıca mevcuttur.

Son Güncelleme

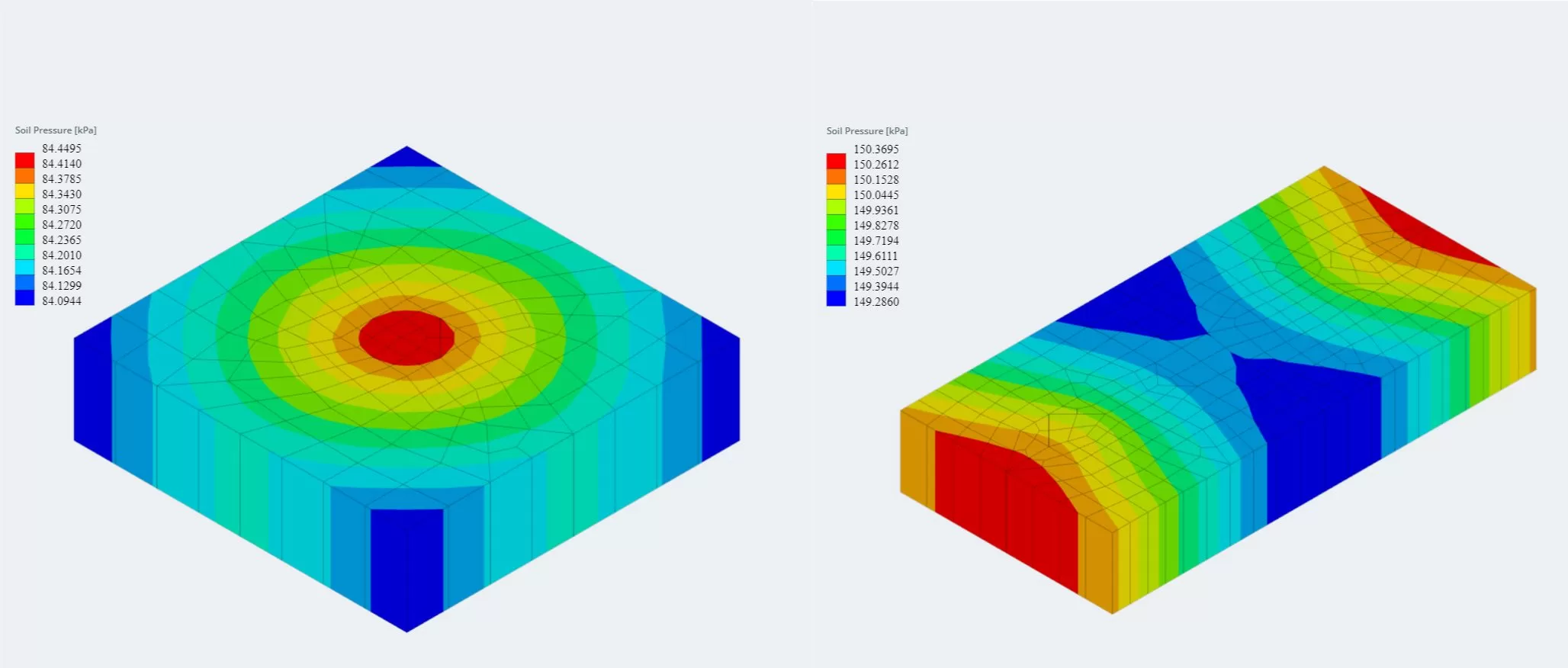
Temel modülünün en son sürümü artık Sonlu Elemanlar Analizi ile entegre edilmiştir (ÇİRKİN), Bu, daha güçlü bir toprak basıncı analizi sunar ve çok daha ayrıntılı bir bükülme kontrolü için kullanılacak ahşap armer analizini sunar. Toprak basıncı ve ahşap armer momentlerine ait FEA sonuçları 3 boyutlu olarak görüntülenebilmekte ve raporlara eklenebilmektedir..

 

SkyCiv’in Temel Tasarım yazılımını denemek ister misiniz?? Ücretsiz aracımız kullanıcıların aşağıdaki işlemleri gerçekleştirmesine olanak tanır: beton temel hesaplamaları herhangi bir indirme veya kurulum gerekmeden!

Ücretsiz Beton Temel Hesaplayıcı

Referanslar:

• güzel, J., İz, N. (2017). Rijit Dikdörtgen Yayılmış Temel Altında Doğrusal Zemin Basıncı Dağılımı için Eksiksiz Analitik Çözüm.
• İstinat duvarına etki eden yanal toprak basıncı, duvar toprak kütlesine itildiğinde pasif kabul edilir., Sonra denklemi kullanın. (2007). İstinat duvarına etki eden yanal toprak basıncı, duvar toprak kütlesine itildiğinde pasif kabul edilir. (7th Baskı). Sonra denklemi kullanın
• Rawat, S., ve. al. (2020). Çift Eksenli Eğilme Altında İzole Dikdörtgen Temeller: Eleştirel Bir Değerlendirme ve Basitleştirilmiş Analiz Metodolojisi.
• Işın, SS. (1995). Betonarme. Blackwell Bilimi