Bir Birleşik temel iki veya daha fazla sütunu destekleyen tek bir temeldir. Birleşik temeller, sütunlar çok yakın aralıklarla yerleştirildiğinde yaygın olarak kullanılır., iki izole temelin tatmin edici olmadığı durumlarda. Örneğin, birbirine çok yakın iki izole temel ile, altındaki toprak, etki bölgelerinin bölümlerini paylaşabilir, Yalıtılmış temellerden birinin veya her ikisinin gerekli bir uzantısına yol açan. Fiziksel veya diğer kısıtlamalara bağlı olarak, El Hesaplamaları Daha Fazla İşlevsellik Gerektirir.

SkyCiv Foundation Design modülü, Amerikan Beton Enstitüsü'ne uygun birleştirilmiş temellerin tasarımını içerir. (ACI 318).

SkyCiv’in Temel Tasarım yazılımını denemek ister misiniz?? Ücretsiz aracımız, kullanıcıların herhangi bir indirme veya kurulum yapmadan yük taşıma hesaplamaları yapmasına olanak tanır!

Temel Tasarım Hesaplayıcı

Birleşik Temel Tasarımı

Boyut Gereksinimleri

İzole bir temelin boyutlarını belirlemek için, servis veya yüklenmemiş yükler, ölü gibi (D), Canlı (L), Rüzgar (W), Sismik (E), vb. Yük Kombinasyonları kullanılarak uygulanacaktır, ACI tarafından tanımlandığı gibi 318-14. Hangi Yük Kombinasyonu geçerli olursa olsun, tasarım yükü olarak kabul edilecektir., ve Denklemde gösterildiği gibi izin verilen toprak basıncıyla karşılaştırılır 1, tavsiye edildiği gibi Bölüm 13.2.6 ACI 318-14.

\(\Metin{q}_{\Metin{a}} = frac{ \Metin{kilo kaybı hikayeleri.net}_{\Metin{n}} + \Metin{kilo kaybı hikayeleri.net}_{\Metin{n}} }{\Metin{Bir}} \sağ ok \) Denklem 1

nerede:
q_a = net izin verilen toprak basıncı
kilo kaybı hikayeleri.net_n = Sütundaki faktörlenmemiş yükler 1 (ayrıldı)
kilo kaybı hikayeleri.net_n = Sütundaki faktörlenmemiş yükler 2 (sağ)
A = Temel alanı

Denklemden 1, q_a ile değişiyorlar Bir.

\(\Metin{Bir} = frac{ \Metin{kilo kaybı hikayeleri.net}_{\Metin{n}} + \Metin{kilo kaybı hikayeleri.net}_{\Metin{n}} }{\Metin{q}_{\Metin{a}}} \sağ ok \) Denklem 1a

Bu noktada, temelin boyutları gerekli alan boyutundan geri hesaplanabilir, Bir.

Tek yönlü Makas

NS Tek yönlü kesme sınır durumu, Ayrıca şöyle bilinir “eğilme kayması”, Kritik bölümü temelin genişliği boyunca uzatır ve bir mesafede bulunur “d” bir sütunun yüzünden, Kritik Düzlem Makas nerede bulunur (Şekle bakın 1).

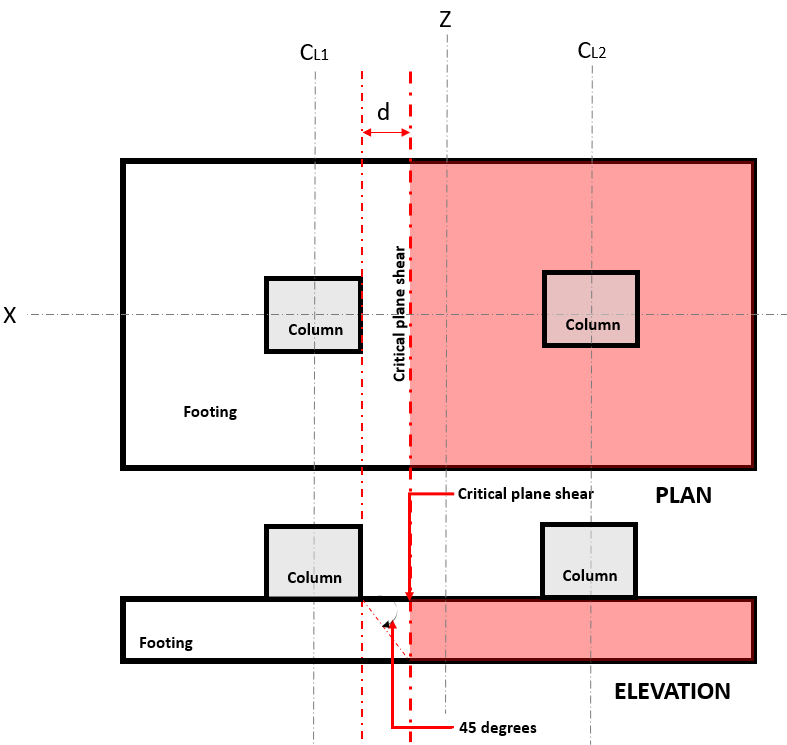
Figür 1. Tek yönlü kesmenin kritik düzlem kesmesi

NS Tek yön Kesme Talep veya V _sen , temelin alanın bulunduğu sütundan uzağa konsolda olduğu varsayılarak hesaplanır. (kırmızı) Şekilde gösterilen 1 göre ACI 318-14, Bölüm 8.5.3.1.1.

NS Tek Yönlü Kesme Kapasitesi veya ϕV_c Nihai kesme dayanımı olarak tanımlanır ve Denklem kullanılarak hesaplanır 2 başına ACI 318-14, Bölüm 22.5.5.1:

\(\phi text{V }_{\Metin{c}} = phi _{\Metin{makaslama}} \zamanlar 2 \sqrt{\Metin{f '}_{\Metin{c}}} \kere metin{b}_{\Metin{w}} \kere metin{d} \sağ ok \) Denklem 2 (ACI Eq. 22.5.5.1 acı)

veya

\(\phi text{V }_{\Metin{c}} = phi _{\Metin{makaslama}} \zamanlar 0.17 \sqrt{\Metin{f '}_{\Metin{c}}} \kere metin{b}_{\Metin{w}} \kere metin{d} \sağ ok \) Denklem 2 (ACI Eq. 22.5.5.1 Metrik)

nerede:
ϕ_makaslama = kesme tasarım faktörü
f’_c = belirtilen beton dayanımı, psi veya MPa
b_w = temelin kalınlığı, inç veya mm
d = aşırı sıkıştırma elyafından uzunlamasına gerilim takviyesinin ağırlık merkezine olan mesafe, inç veya mm

Kesme Talebi ve Kesme Kapasitesi, ACI tasarım gereksinimlerini karşılamak için aşağıdaki denklemi karşılamalıdır 318-14:

\(\Metin{V }_{\Metin{sen}} \leq phi text{V }_{\Metin{c}} \sağ ok \) Denklem 3 (ACI Eq. 7.5.1.1(b))

SkyCiv Vakfı, Denklem uyumlu 3, tek yönlü kayma birimi oranını hesaplar (Denklem 4) Kesme Kapasitesi yerine Kesme Talebini alarak.

\( \Metin{oran} = frac{\Metin{Kesme Talebi}}{\Metin{Kesme Kapasitesi}} \sağ ok \) Denklem 4

İki yönlü Makas

NS İki yönlü Makas sınır durumu, Ayrıca şöyle bilinir “delme makası”, kritik bölümü kolonun yüzünden ve kolonun çevresinden “d/2” kadar uzatır. Kritik Kayma Düzlemi, temelin bu bölümünde bulunur (Şekle bakın 2).

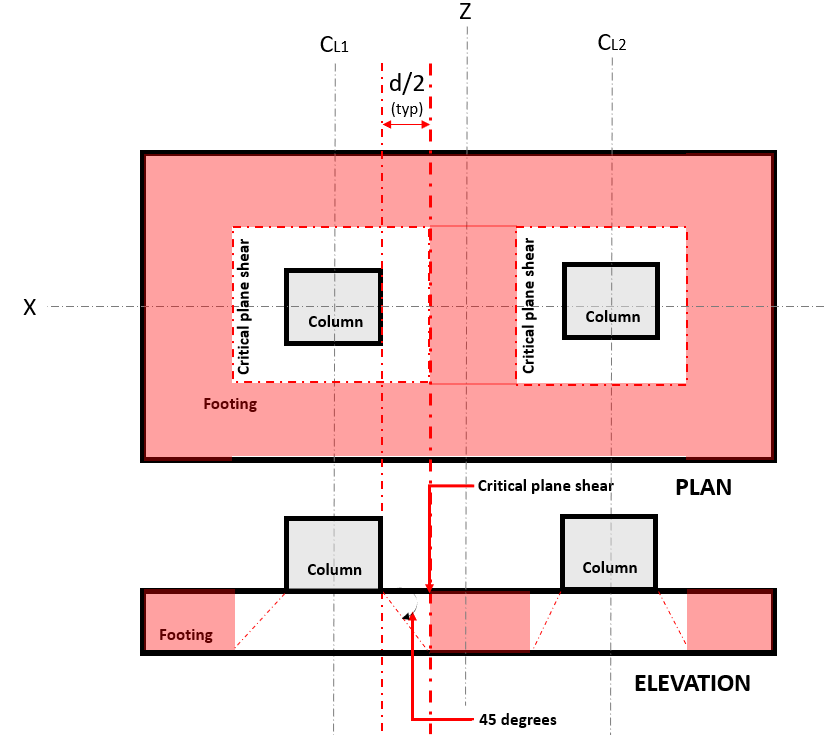
Figür 2. İki yönlü kesmenin kritik düzlem kesmesi

NS İki yolTalebi duymak veya V _sen Kritik Kesme Düzleminde meydana gelir, "d/2" uzaklıkta bulunan (kırmızı) taranmış alan, Şekilde gösterilen 2, göre ACI 318-14, Bölüm 22.6.4.

NS Kesme Kapasitesi veya ϕV_c Denklem kullanılarak hesaplanan en küçük değer tarafından yönetilir 5, 6, ve 7 başına ACI 318-14, Bölüm 22.6.5.2:

\(\phi text{V }_{\Metin{c}} = phi _{\Metin{makaslama}} \zamanlar 4 \times lambda times sqrt{\Metin{f '}_{\Metin{c}}} \sağ ok \) Denklem 5 (ACI Eq. 22.6.5.2(a) acı)

\(\phi text{V }_{\Metin{c}} = sol ( 2 + \çatlamak{4}{\beta } \sağ ) \times lambda times sqrt{f’_{c}} \sağ ok \) Denklem 6 (ACI Eq. 22.6.5.2(b) acı)

\(\phi text{V }_{\Metin{c}} = sol ( 2 + \çatlamak{\alpha _{s} \kere d }{b{Ö}} \sağ ) \times lambda times sqrt{f’_{c}} \sağ ok \) Denklem 7 (ACI Eq. 22.6.5.2(c) acı)

veya

\(\phi text{V }_{\Metin{c}} = phi _{\Metin{makaslama}} \zamanlar 0.33 \times lambda times sqrt{\Metin{f '}_{\Metin{c}}} \sağ ok \) Denklem 5 (ACI Eq. 22.6.5.2(a) Metrik)

\(\phi text{V }_{\Metin{c}} = 0.17 \kez kaldı ( 1 + \çatlamak{2}{\beta } \sağ ) \times lambda times sqrt{f’_{c}} \sağ ok \) Denklem 6 (ACI Eq. 22.6.5.2(b) Metrik)

\(\phi text{V }_{\Metin{c}} = 0.0083 \kez kaldı ( 2 + \çatlamak{\alpha _{s} \kere d }{b{Ö}} \sağ ) \times lambda times sqrt{f’_{c}} \sağ ok \) Denklem 7 (ACI Eq. 22.6.5.2(c) Metrik)

Not: β kolonun uzun kenarının kısa kenarına oranıdır, konsantre yük, veya reaksiyon alanı ve α_s verilmiş 22.6.5.3

nerede:
λ = aynı basınç dayanımına sahip normal ağırlıklı betona göre hafif betonun azaltılmış mekanik özelliklerini yansıtan modifikasyon faktörü
f’_c = belirtilen beton dayanımı, psi veya MPa
d = aşırı sıkıştırma elyafından uzunlamasına gerilim takviyesinin ağırlık merkezine olan mesafe, veya mm

Kesme Talebi ve Kesme Kapasitesi, ACI tasarım gereksinimlerini karşılamak için aşağıdaki denklemi karşılamalıdır 318-14:

\(\Metin{V }_{\Metin{sen}} \leq phi text{V }_{\Metin{c}} \sağ ok \) Denklem 8 (ACI Eq. 7.5.1.1(b))

SkyCiv Vakfı, Denklem uyumlu 8, iki yönlü kayma birim oranını hesaplar (Denklem 9) Kesme Kapasitesi yerine Kesme Talebini alarak.

\( \Metin{oran} = frac{\Metin{Kesme Talebi}}{\Metin{Kesme Kapasitesi}} \sağ ok \) Denklem 9

Eğilme

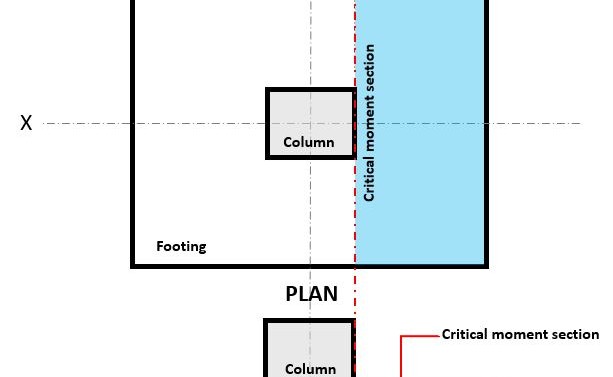
Figür 3. Flexure'ın kritik moment bölümü

NS Eğilme sınır durumu şu saatte oluşur Kritik Eğilme Bölümü, temelin üstünde sütunun yüzünde bulunur (Şekle bakın 3).

NS Eğilme Talebi, veya M_sen Kritik Eğilme Bölümünde bulunur (mavi tarama alanı) Şekilde gösterilen 3, ve Denklem kullanılarak hesaplanır 10:

\( \Metin{M}_{sen} = text{q}_{sen} \kez kaldı ( \çatlamak{l_{x}}{2} – \çatlamak{c_{x}}{2} \sağ ) \kere l_{ile} \kez kaldı ( \çatlamak{\çatlamak{l_{x}}{2} – \çatlamak{c_{x}}{2} }{2} \sağ ) \sağ ok \) Denklem 10

nerede:
q_sen = faktörlü toprak basıncı, ksf veya kpa
l_x = x eksenine paralel temel boyutu, inç veya mm
l_ile = z eksenine paralel temel boyutu, inç veya mm
c_x = x eksenine paralel sütun boyutu, inç veya mm

NS Eğilme Kapasitesi, veya ϕMn Denklem kullanılarak hesaplanır 11:

\( \phi text{M}_{n} = phi_{\Metin{eğilme}} \kere A_{s} \kere f_{Y} \kez kaldı( d – \çatlamak{a}{2} \sağ) \sağ ok \) Denklem 11

nerede:
ϕ = eğilme tasarım faktörü
l_x = x eksenine paralel temel boyutu, inç veya mm
l_ile = z eksenine paralel temel boyutu, inç veya mm
d = aşırı sıkıştırma elyafından uzunlamasına gerilim takviyesinin ağırlık merkezine olan mesafe, inç veya mm
Bir_s = takviye alanı, içinde² veya mm²
a = eşdeğer dikdörtgen gerilme bloğunun derinliği, inç veya mm
fy = çelik mukavemeti, ksi veya MPa

Referanslar

1. Yapısal Beton için Bina Kodu Gereklilikleri (ACI 318-14) Yapısal Beton için Yapı Kodu Gerekliliklerine İlişkin Yorum (ACI 318R-14). Amerikan Beton Enstitüsü, 2014.
2. McCormac, Jack C., ve Russell H. Kahverengi. Betonarme ACI Tasarımı 318-11 Kod Sürümü. Wiley, 2014.
3. Taylor, Andrew, ve diğerleri. Betonarme Tasarım El Kitabı: ACI-318-14 için bir Arkadaş. Amerikan Beton Enstitüsü, 2015.