EN kullanan baz plaka tasarım örneği 1993-1-8:2005, İÇİNDE 1993-1-1:2005, İÇİNDE 1992-1-1:2004, ve EN 1992-4:2018.
Sorun Bildirimi
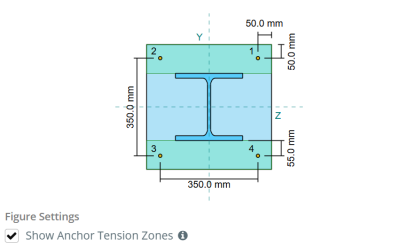
50 kn gerilimli bir yük için tasarlanmış sütun-taban plakası bağlantısının yeterli olup olmadığını belirleyin.
Verilen Veriler
Sütun:
Sütun bölümü: O 240 B
Sütun alanı: 10600 mm2
Sütun malzemesi: S235
Taban plakası:
Taban plaka boyutları: 450 mm x 450 mm
Taban plakası kalınlığı: 20 mm
Taban plaka malzemesi: S235
Izgara:
Grout kalınlığı: 20 mm
Somut:
Somut boyutlar: 500 mm x 500 mm
Beton kalınlığı: 350 mm
Beton malzeme: C25/30
Çatlamış veya çatlaksız: Çatlak
Çapa:
Çapa: 12 mm
Etkili gömme uzunluğu: 300.0 mm
Gömülü plaka çapı: 60 mm
Gömülü plaka kalınlığı: 10 mm
Çapa: 8.8
Diğer bilgiler:
- Kez olmayan çapalar.
- Kesilmiş ipliklerle çapa.
Kaynaklar:
Kaynak tipi: FPBW
Dolgu Metal Sınıflandırması: E35
Çapa Verileri (itibaren SkyCiv Hesap Makinesi):
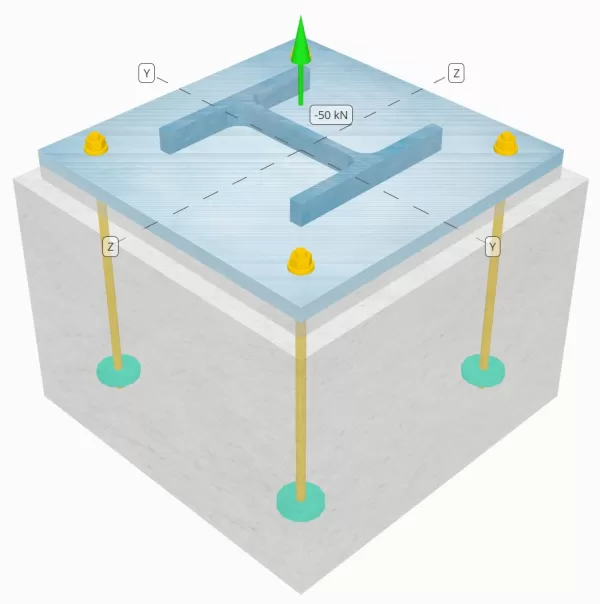
SkyCiv Ücretsiz Aracındaki Model
Ücretsiz çevrimiçi aracımızı kullanarak yukarıdaki taban plakası tasarımını bugün modelleyin! Kayıt olmanıza gerek yok.
Tanımlar
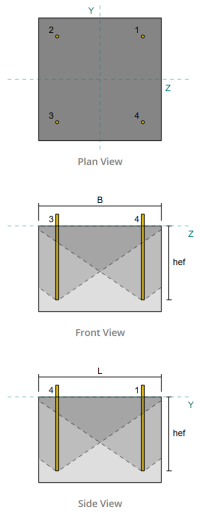
Çapa gerilim bölgesi:
İçinde SkyCiv Taban Plakası Tasarım Yazılımı, sadece içinde bulunan ankrajlar çapa gerilim bölgesi yükselişe direnmede etkili kabul edilir. Bu bölge tipik olarak sütun flanşlarının veya web'in yakınındaki alanları içerir. Bu bölgenin dışındaki ankrajlar gerilim direncine katkıda bulunmaz ve yükselme hesaplamalarından hariç tutulur.
Varsayım, yükselme kuvvetinin plakadan nasıl yayıldığını tahmin ederek taban plakası analizini basitleştirir..
Çapa:
NS SkyCiv Taban Plakası Tasarım Yazılımı Hangi çapaların değerlendirmek için bir çapa grubunun parçası olduğunu belirleyen sezgisel bir özellik içerir. beton patlaması ve beton yan yüzlü patlama başarısızlık.
Bir çapa Benzer etkili gömme derinlikleri ve aralıklı çoklu ankrajlardan oluşur, ve onların Öngörülen direnç alanları örtüşüyor. Çapalar gruplandığında, Gruba uygulanan toplam gerilim kuvvetine direnmek için kapasiteleri birleştirilir.
Gruplama kriterlerini karşılamayan çapalar, tek çapa. Bu durumda, Sadece bireysel çapa üzerindeki gerilim kuvveti kendi etkili direnç alanına göre kontrol edilir.
Adım adım hesaplamalar
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #1: Kaynak kapasitesini hesapla
Verilen bilgilerden, Bu tasarım örneğinde kullanılan kaynak bir Tam penetrasyon popo kaynağı (FPBW). Kaynak direncini belirlemek için sütunun ve taban plakasının temel metal kapasitelerini hesaplayacağız.. Bunu yapmak için, Önce hesaplamamız gerekiyor Toplam kaynak uzunluğu sütunda ve kaynak stresini elde edin.
\(
F_{w,Ed} = frac{N_x}{2 b_f t_f + \ayrıldı( d_{seri} – 2 T_F – 2 r_{seri} \sağ) t_w}
\)
\(
F_{w,Ed} = frac{50 \, \Metin{kN}}{2 \zamanlar 240 \, \Metin{mm} \zamanlar 17 \, \Metin{mm} + \ayrıldı( 240 \, \Metin{mm} – 2 \zamanlar 17 \, \Metin{mm} – 2 \zamanlar 21 \, \Metin{mm} \sağ) \zamanlar 10 \, \Metin{mm}} = 5.102 \, \Metin{MPa}
\)
Sonraki, Belirliyoruz gerilme mukavemeti kolon ve taban plakası arasındaki zayıf malzemenin.
\(
f_y = min ( f_{Y,\Metin{seri}}, f_{Y,\Metin{bp}} \sağ) = dak sol( 225 \, \Metin{MPa}, 225 \, \Metin{MPa} \sağ) = 225 \, \Metin{MPa}
\)
Sonra kullanıyoruz İÇİNDE 1993-1-8:2005 Madde 4.7.1 ve İÇİNDE 1993-1-1:2005 Eşitlik. 6.6 FPBW tasarım kaynak direncini hesaplamak için.
\(
F_{w,RD3} = frac{f_y}{\gama_{M0}} = frac{225 \, \Metin{MPa}}{1} = 225 \, \Metin{MPa}
\)
Dan beri 5.102 MPa < 225 MPa, Kaynak kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #2: Gerginlik yükü nedeniyle taban plakası eğilme verme kapasitesini hesaplayın
hesaplamak için Taban plakası bükülme kapasitesi gerginlik yüküne karşı, kullanacağız Verim Çizgisi Desenleri dairesel desenler ve dairesel olmayan desenler gibi. Sonra, Yönetim kapasitesini belirliyoruz, Nöbet Kuvvetleri olmadığını varsaymak, Plakanın akma mukavemetini ankraj cıvatalarının gerilme direnci ile karşılaştırarak.
Başlamak, Gerekli olanı hesaplıyoruz boyutlar Verilen cıvata düzenine dayanarak. Anmak İÇİNDE 1992-1-8:2005 Tablo 6.2 rehberlik için.
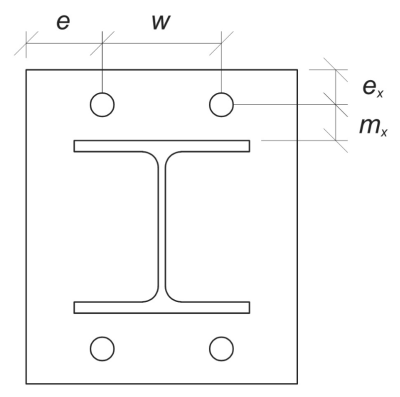
\(
m_x = frac{S_ – d_{seri}}{2} = frac{350 \, \Metin{mm} – 240 \, \Metin{mm}}{2} = 55 \, \Metin{mm}
\)
\(
w = s_z ( N_{a,\Metin{taraf}} – 1 \sağ) = 350 \, \Metin{mm} \kez kaldı( 2 – 1 \sağ) = 350 \, \Metin{mm}
\)
\(
E_X = frac{L_{bp} – S_}{2} = frac{450 \, \Metin{mm} – 350 \, \Metin{mm}}{2} = 50 \, \Metin{mm}
\)
\(
e = frak{B_{bp} – w}{2} = frac{450 \, \Metin{mm} – 350 \, \Metin{mm}}{2} = 50 \, \Metin{mm}
\)
\(
b_p = b_{bp} = 450 \, \Metin{mm}
\)
Ayrıca taban plakasındaki çapa kenarı mesafesini hesaplayalım, bu da sınırlıdır \( M_X \) başına boyut
\(
n = min sol( eski, 1.25 M_X Right) = dak sol( 50 \, \Metin{mm}, 1.25 \zamanlar 55 \, \Metin{mm} \sağ) = 50 \, \Metin{mm}
\)
Sonra, Aşağıdakilerin etkili uzunluklarını hesaplıyoruz dairesel desenler (başvurmak SCI P398 Tablosu 5.3).
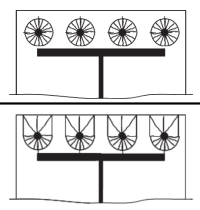
Dairesel desen 1:
\(
l_{eff,CP1} = n_{a,\Metin{taraf}} \pi m_x = 2 \Times pi Times 55 \, \Metin{mm} = 345.58 \, \Metin{mm}
\)
Dairesel desen 2:
\(
l_{eff,CP2} = sol( \çatlamak{N_{a,\Metin{taraf}}}{2} \sağ) (\Pi M_X + 2 eski) = sol( \çatlamak{2}{2} \sağ) \zamanlar (\Pi Times 55 \, \Metin{mm} + 2 \zamanlar 50 \, \Metin{mm}) = 272.79 \, \Metin{mm}
\)
Yöneten dairesel desen etkili uzunluk:
\(
l_{eff,cp} = min (l_{eff,CP1}, l_{eff,CP2}) = min (345.58 \, \Metin{mm}, 272.79 \, \Metin{mm}) = 272.79 \, \Metin{mm}
\)
Şimdi, Aşağıdakilerin etkili uzunluklarını hesaplıyoruz dairesel olmayan desenler (başvurmak SCI P398 Tablosu 5.3)
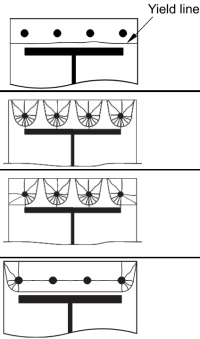
Dairesel olmayan desen 1:
\(
l_{eff,NC1} = frac{B_P}{2} = frac{450 \, \Metin{mm}}{2} = 225 \, \Metin{mm}
\)
Dairesel olmayan desen 2:
\(
l_{eff,NC2} = sol( \çatlamak{N_{a,\Metin{taraf}}}{2} \sağ) (4 M_X + 1.25 eski) = sol( \çatlamak{2}{2} \sağ) \zamanlar (4 \zamanlar 55 \, \Metin{mm} + 1.25 \zamanlar 50 \, \Metin{mm}) = 282.5 \, \Metin{mm}
\)
Dairesel olmayan desen 3:
\(
l_{eff,NC3} = 2 M_X + 0.625 eski + e = 2 \zamanlar 55 \, \Metin{mm} + 0.625 \zamanlar 50 \, \Metin{mm} + 50 \, \Metin{mm} = 191.25 \, \Metin{mm}
\)
Dairesel olmayan desen 4:
\(
l_{eff,NC4} = 2 M_X + 0.625 eski + \çatlamak{(N_{a,\Metin{taraf}} – 1) S_Z}{2} = 2 \zamanlar 55 \, \Metin{mm} + 0.625 \zamanlar 50 \, \Metin{mm} + \çatlamak{(2 – 1) \zamanlar 350 \, \Metin{mm}}{2} = 316.25 \, \Metin{mm}
\)
Yönetici Dairesel Olmayan Desen etkili uzunluk:
\(
l_{eff,NC} = min (l_{eff,NC1}, l_{eff,NC2}, l_{eff,NC3}, l_{eff,NC4}) = min (225 \, \Metin{mm}, 282.5 \, \Metin{mm}, 191.25 \, \Metin{mm}, 316.25 \, \Metin{mm}) = 191.25 \, \Metin{mm}
\)
Sonra, Dairesel ve dairesel olmayan desenlerin etkili uzunlukları arasındaki daha az değeri belirleriz.
\(
l_{eff,1} = min (l_{eff,cp}, l_{eff,NC}) = min (272.79 \, \Metin{mm}, 191.25 \, \Metin{mm}) = 191.25 \, \Metin{mm}
\)
Şimdi, Bu hesaplanmış etkili uzunluğu, eğilme verim direncini hesaplamak için kullanıyoruz. Göre İÇİNDE 1993-1-8:2005 Tablo 6.2, Arıza modu için plaka moment direnci 1 dır-dir:
\(
M_{lütfen,1,Yol} = frac{0.25 l_{eff,1} (t_{bp})^2 f_{ve _bp}}{\gama_{M0}} = frac{0.25 \zamanlar 191.25 \, \Metin{mm} \zamanlar (20 \, \Metin{mm})^2 Times 225 \, \Metin{MPa}}{1} = 4303.1 \, \Metin{kN} \cdot metin{mm}
\)
Varsayarak Meraklı Yok, EN kullanıyoruz 1993-1-8:2005 Tablo 6.2 belirlemek için tasarım taban plakasının direnci başarısızlık için Modlar 1 ve 2.
\(
F_{T,1,Yol} = frac{2 M_{lütfen,1,Yol}}{M_X} = frac{2 \zamanlar 4303.1 \, \Metin{kN} \cdot metin{mm}}{55 \, \Metin{mm}} = 156.48 \, \Metin{kN}
\)
Sonra, Ankraj çubuğunun gerilme direncini kullanarak hesaplıyoruz. İÇİNDE 1992-4:2018 Madde 7.2.1.3. Bu, sonraki çapa kontrollerinde daha ayrıntılı olacak.
\(
F_{t,Yol} = frac{C K_2 F_{u _anc} Olarak}{\gama_{M2, çapa}} = frac{0.85 \zamanlar 0.9 \zamanlar 800 \, \Metin{MPa} \zamanlar 113.1 \, \Metin{mm}^ 2}{1.25} = 55.372 \, \Metin{kN}
\)
Daha sonra hesaplamak için ankraj çubuğu başına direnci kullanacağız. taban plakasının tasarım direnci başarısızlık altında mod 3, toplam cıvata arızası.
\(
F_{T,3,Yol} = n_{a,taraf} F_{t,Yol} = 2 \zamanlar 55.372 \, \Metin{kN} = 110.74 \, \Metin{kN}
\)
En sonunda, Arıza modları arasındaki yönetici direnç değerini belirleriz.
\(
F_{T,Yol} = min (F_{T,1,Yol}, F_{T,3,Yol}) = min (156.48 \, \Metin{kN}, 110.74 \, \Metin{kN}) = 110.74 \, \Metin{kN}
\)
Hesaplanıyor Flanş başına gerilim yükü, sahibiz:
\(
F_{T,Ed} = frac{N_x}{2} = frac{50 \, \Metin{kN}}{2} = 25 \, \Metin{kN}
\)
Dan beri 25 kN < 110.74 kN, taban plakası bükülme verim kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #3: Ankraj çubuğu gerilme kapasitesini hesaplayın
Ankraj çubuğu gerilme kapasitesinin değerini zaten biliyoruz, Ama daha ayrıntılı olarak ele alalım.
İlk, Ankraj çubuğunun gerilme gerilimi alanını hesaplayalım.
\(
A_s = frac{\pi}{4} (d_{anc})^2 = frac{\pi}{4} \zamanlar (12 \, \Metin{mm})montaj yüksekliğinde 113.1 \, \Metin{mm}^ 2
\)
Sonra, Değerleri uygulayalım \( c \) faktör ve \( Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{2} \) faktör. Bu değerler SkyCiv Base Plaka Tasarım Yazılımının ayarlarında değiştirilebilir. Ücretsiz sürümü burada deneyin.
- \( c = 0.85 \) Kesilmiş dişleri olan ankrajlar için
- \( Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{2} = 0.9\) Küvet olmayan çapa için
Şimdi, Hadi Kullanalım İÇİNDE 1992-4:2018 Madde 7.2.1.3 hesaplamak için Ankraj çubuğunun tasarım direnci gerginlikte.
\(
N_{Yol,s} = frac{C K_2 F_{u _anc} Olarak}{\gama_{M2, çapa}} = frac{0.85 \zamanlar 0.9 \zamanlar 800 \, \Metin{MPa} \zamanlar 113.1 \, \Metin{mm}^ 2}{1.25} = 55.372 \, \Metin{kN}
\)
Hesaplanıyor Ankraj başına gerilim yükü, sahibiz:
\(
N_{Ed} = frac{N_x}{N_{a,t}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Dan beri 12.5 kN < 55.372 kN, Ankraj çubuğu gerilme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #4: Gerginlikte beton kırılma kapasitesini hesaplayın

Kırılma kapasitesini hesaplamadan önce, Öncelikle üyenin bir dar üye. Göre İÇİNDE 1992-4:2008 Madde 7.2.1.4(8), Üye, dar bir üye için kriterleri karşılıyor. Bu nedenle, a değiştirilmiş Etkili gömme uzunluğu Breakout kapasitesi hesaplamalarında kullanılmalıdır. Bu ayar aynı zamanda karakteristik aralık ve karakteristik kenar mesafesi, buna göre değiştirilmesi gereken.
Dar üye kriterlerine göre, NS değiştirilmiş değerler Çünkü çapa grubu aşağıdaki gibidir:
- Modifiye Etkili Gömme Uzunluğu, \( H'_{ef} = 100 mm \)
- değiştirilmiş karakteristik aralık, \( S'_{sonucu AISI S100-12'ye göre hesaplayacaktır} = 300 mm )
- değiştirilmiş karakteristik kenar mesafesi, \( C'_{sonucu AISI S100-12'ye göre hesaplayacaktır} = 150 mm )
kullanma İÇİNDE 1992-4:2018 Eşitlik. 7.3, hesaplıyoruz referans yansıtılan beton koni alanı tek bir çapa için.
\(
A0_{c,N} = s’_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} S'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} = 350 \, \Metin{mm} \zamanlar 350 \, \Metin{mm} = 122500 \, \Metin{mm}^ 2
\)
benzer şekilde, hesaplıyoruz gerçek öngörülen beton koni alanı çapa grubunun.
\(
bir_{Nc} = L_{Nc} B_{Nc} = 500 \, \Metin{mm} \zamanlar 500 \, \Metin{mm} = 250000 \, \Metin{mm}^ 2
\)
Nerede,
\(
L_{Nc} = dak sol( c_{ayrıldı,G1}, C'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} \sağ)
+ \ayrıldı( \Min Sol( S_{toplam,ile,G1}, S'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} \ayrıldı( N_{ile,G1} – 1 \sağ) \sağ) \sağ)
+ \Min Sol( c_{sağ,G1}, C'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} \sağ)
\)
\(
L_{Nc} = dak sol( 75 \, \Metin{mm}, 175 \, \Metin{mm} \sağ)
+ \ayrıldı( \Min Sol( 350 \, \Metin{mm}, 350 \, \Metin{mm} \zamanlar (2 – 1) \sağ) \sağ)
+ \Min Sol( 75 \, \Metin{mm}, 175 \, \Metin{mm} \sağ)
\)
\(
L_{Nc} = 500 \, \Metin{mm}
\)
\(
B_{Nc} = dak sol( c_{üst,G1}, C'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} \sağ)
+ \ayrıldı( \Min Sol( S_{toplam,Y,G1}, S'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} \ayrıldı( N_{Y,G1} – 1 \sağ) \sağ) \sağ)
+ \Min Sol( c_{alt,G1}, C'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1} \sağ)
\)
\(
B_{Nc} = dak sol( 75 \, \Metin{mm}, 175 \, \Metin{mm} \sağ)
+ \ayrıldı( \Min Sol( 350 \, \Metin{mm}, 350 \, \Metin{mm} \zamanlar (2 – 1) \sağ) \sağ)
+ \Min Sol( 75 \, \Metin{mm}, 175 \, \Metin{mm} \sağ)
\)
\(
B_{Nc} = 500 \, \Metin{mm}
\)
Sonraki, değerlendiriyoruz karakteristik güç kullanan tek bir çapanın İÇİNDE 1992-4:2018 Eşitlik. 7.2
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} = k_1 sqrt{\çatlamak{f_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}}{\Metin{MPa}}} \ayrıldı( \çatlamak{H'_{ef,G1}}{\Metin{mm}} \sağ)^{1.5} N
\)
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} = 8.9 \kez sqrt{\çatlamak{25 \, \Metin{MPa}}{1 \, \Metin{MPa}}} \kez kaldı( \çatlamak{116.67 \, \Metin{mm}}{1 \, \Metin{mm}} \sağ)^{1.5} \zamanlar 0.001 \, \Metin{kN} = 56.076 \, \Metin{kN}
\)
Nerede,
- \(Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{1} = 8.9\) dökme ankrajlar için
Şimdi, Gerekli olanı hesaplayarak geometrinin etkilerini değerlendiriyoruz parametreleri Breakout direnci için.
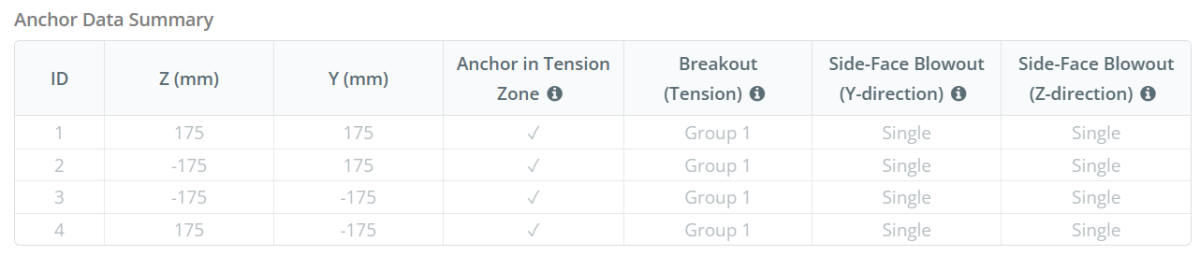
Çapa grubunun en kısa kenar mesafesi olarak belirlenir.:
\(
c_{min,N} = dak sol( c_{ayrıldı,G1}, c_{sağ,G1}, c_{üst,G1}, c_{alt,G1} \sağ)
= dak sol( 87.5 \, \Metin{mm}, 87.5 \, \Metin{mm}, 150 \, \Metin{mm}, 150 \, \Metin{mm} \sağ)
= 87.5 \, \Metin{mm}
\)
Göre İÇİNDE 1992-4:2018 Eşitlik. 7.4, Betondaki stresin dağılımını hesaba katan parametrenin değeri:
\(
\Psi_{s,N} = dak sol( 0.7 + 0.3 \ayrıldı( \çatlamak{c_{min,N}}{C'_{sonucu AISI S100-12'ye göre hesaplayacaktır,G1}} \sağ), 1.0 \sağ)
= dak sol( 0.7 + 0.3 \kez kaldı( \çatlamak{75 \, \Metin{mm}}{175 \, \Metin{mm}} \sağ), 1 \sağ)
= 0.82857
\)
NS Kabuk Spalling Etkisi kullanılmak üzere muhasebeleştirilir İÇİNDE 1992-4:2018 Eşitlik. 7.5, verme:
\(
\Psi_{= c times A_,N} = dak sol( 0.5 + \çatlamak{H'_{ef,G1}}{\Metin{mm} \, / \, 200}, 1.0 \sağ)
= dak sol( 0.5 + \çatlamak{116.67 \, \Metin{mm}}{1 \, \Metin{mm} \, / \, 200}, 1 \sağ)
= 1
\)
Ek olarak, her ikisi de eksantriklik faktörü ve Sıkıştırma etki faktörü olarak alınır:
\(
\Psi_{ec,N} = 1
\)
\(
\Psi_{M,N} = 1
\)
Daha sonra tüm bu faktörleri birleştiriyoruz ve uyguluyoruz GİBİ 5216:2021 Denklem 6.2.3.1 değerlendirmek için Tasarım Beton Koni Kırılma Direnci Çapa grubu için:
\(
N_{Yol,c} = frac{N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} \ayrıldı( \çatlamak{bir_{Nc}}{A0_{c,N}} \sağ) \Psi_{s,N} \Psi_{= c times A_,N} \Psi_{ec,N} \Psi_{M,N}}{\gama_{= c times A_}}
\)
\(
N_{Yol,c} = frac{56.076 \, \Metin{kN} \kez kaldı( \çatlamak{250000 \, \Metin{mm}^ 2}{122500 \, \Metin{mm}^ 2} \sağ) \zamanlar 0.82857 \zamanlar 1 \zamanlar 1 \zamanlar 1}{1.5} = 63.215 \, \Metin{kN}
\)
NS Toplam uygulanan gerilim yükü Ankraj grubunda, ankraj başına gerilim yükünün ankraj sayısı ile çarpılmasıyla hesaplanır.:
\(
N_{FA} = sol( \çatlamak{N_x}{N_{a,t}} \sağ) N_{a,G1} = sol( \çatlamak{50 \, \Metin{kN}}{4} \sağ) \zamanlar 4 = 50 \, \Metin{kN}
\)
Dan beri 50 kN < 63.215 kN Beton kırılma kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #5: Çapa çekme kapasitesini hesaplayın
NS çekilme kapasitesi bir çapanın, gömülü ucundaki direnç tarafından yönetilir. Başlamak, hesaplıyoruz rulman alanı gömülü plakanın, Ankraj çubuğu tarafından işgal edilen alanı çıkardıktan sonra net alan.
İlk, Çekme direnci için etkili maksimum ankraj kafası boyutunu hesaplıyoruz, göre İÇİNDE 1992-4:2018 Madde 7.2.1.5 Not.
\(
d_{h,\Metin{max}} = dak sol( b_{\Metin{Gömme _plate}}, 6 \ayrıldı( t_{\Metin{Gömme _plate}} \sağ) + d_{\Metin{anc}} \sağ)
= dak sol( 60 \, \Metin{mm}, 6 \zamanlar (10 \, \Metin{mm}) + 12 \, \Metin{mm} \sağ)
= 60 \, \Metin{mm}
\)
Sonraki, Dairesel gömülü plakanın net yatak alanını kullanarak hesaplıyoruz.:
\(
bir_{brg} = frac{\pi}{4} \ayrıldı( \ayrıldı( d_{h,\Metin{max}} \sağ)^ 2 – \ayrıldı( d_{\Metin{anc}} \sağ)^2 doğru)
\)
\(
bir_{brg} = frac{\pi}{4} \kez kaldı( \ayrıldı( 60 \, \Metin{mm} \sağ)^ 2 – \ayrıldı( 12 \, \Metin{mm} \sağ)^2 doğru) = 2714.3 \, \Metin{mm}^ 2
\)
Sonra hesaplıyoruz Tasarım Beton çekme direnci gerginlik içinde döküm ankrajı İÇİNDE 1992-4:2018 Madde 7.2.1.5:
\(
N_{Yol,s} = frac{K_2 A_{brg} f_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}}{\gama_{Milletvekili}}
= frac{7.5 \zamanlar 2714.3 \, \Metin{mm}^2 Times 25 \, \Metin{MPa}}{1.5}
= 339.29 \, \Metin{kN}
\)
Daha önce hesaplananları hatırlayın Ankraj başına gerilim yükü:
\(
N_{Ed} = frac{N_x}{N_{a,t}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Dan beri 12.5 kN < 339.29 kN, Çapa çekme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #6: Y yönünde yan yüz patlama kapasitesini hesaplayın

Ankraj kimliğini düşünelim #3. Kenar mesafesini hesaplayarak başlıyoruz. başarısızlık kenarı.
\(
c_{ile,\Metin{min}} = dak sol( c_{\Metin{ayrıldı,kip-ft}}, c_{\Metin{sağ,kip-ft}} \sağ)
= dak sol( 75 \, \Metin{mm}, 425 \, \Metin{mm} \sağ)
= 75 \, \Metin{mm}
\)
Sonraki, Kenar mesafesini belirliyoruz dik uç.
\(
c_{Y,\Metin{min}} = dak sol( c_{\Metin{üst,kip-ft}}, c_{\Metin{alt,kip-ft}} \sağ)
= dak sol( 425 \, \Metin{mm}, 75 \, \Metin{mm} \sağ)
= 75 \, \Metin{mm}
\)
kullanma İÇİNDE 1992-4:2018 Eşitlik. 7.27, Hadi hesaplayalım Referans Yansıtılan Alan tek bir bağlantı elemanı.
\(
A0_{c,NB} = sol( 4 c_{ile,\Metin{min}} \sağ)^ 2
= sol( 4 \zamanlar 75 \, \Metin{mm} \sağ)^ 2
= 90000 \, \Metin{mm}^ 2
\)
Çapa grubunun kapasitesini kontrol ettiğimiz için, Hadi alalım Gerçek öngörülen alan Çapa grubunun İÇİNDE 1992-4:2018 Eşitlik. 7.27.
\(
bir_{Nc} = B_{c,NB} H_{c,NB} = 225 \, \Metin{mm} \zamanlar 200 \, \Metin{mm} = 45000 \, \Metin{mm}^ 2
\)
Nerede,
\(
B_{c,NB} = 2 c_{ile,\Metin{min}} + \Min Sol( 2 c_{ile,\Metin{min}}, c_{Y,\Metin{min}} \sağ)
= 2 \zamanlar 75 \, \Metin{mm} + \Min Sol( 2 \zamanlar 75 \, \Metin{mm}, 75 \, \Metin{mm} \sağ)
= 225 \, \Metin{mm}
\)
\(
H_{c,NB} = 2 c_{ile,\Metin{min}} + \ayrıldı( \Min Sol( t_{\Metin{conc}} – h_{\Metin{ef}}, 2 c_{ile,\Metin{min}} \sağ) \sağ)
= 2 \zamanlar 75 \, \Metin{mm} + \ayrıldı( \Min Sol( 350 \, \Metin{mm} – 300 \, \Metin{mm}, 2 \zamanlar 75 \, \Metin{mm} \sağ) \sağ)
= 200 \, \Metin{mm}
\)
Hesaplamada karakteristik beton patlama gücü bireysel bir çapa, kullanacağız İÇİNDE 1992-4:2018 Eşitlik. 7.26.
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = k_5 ( \çatlamak{c_{ile,\Metin{min}}}{\Metin{mm}} \sağ)
\ayrıldı( \sqrt{\çatlamak{bir_{\Metin{brg}}}{\Metin{mm}^ 2}} \sağ)
\ayrıldı( \sqrt{\çatlamak{f_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}}{\Metin{MPa}}} \sağ) N
\)
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = 8.7 \kez kaldı( \çatlamak{75 \, \Metin{mm}}{1 \, \Metin{mm}} \sağ)
\kez kaldı( \sqrt{\çatlamak{2714.3 \, \Metin{mm}^ 2}{1 \, \Metin{mm}^ 2}} \sağ)
\kez kaldı( \sqrt{\çatlamak{25 \, \Metin{MPa}}{1 \, \Metin{MPa}}} \sağ)
\zamanlar 0.001 \, \Metin{kN}
\)
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = 169.97 \, \Metin{kN}
\)
Sonra, Biz alacağız Yan yüzlü patlama parametreleri.
Streslerin betondaki dağılımının bozulmasının muhasebesi parametre hesaplanabilir. İÇİNDE 1992-4:2018 Eşitlik. 7.28.
\(
\Psi_{s,NB} = dak sol( 0.7 + 0.3 \ayrıldı( \çatlamak{c_{Y,\Metin{min}}}{2 c_{ile,\Metin{min}}} \sağ), 1.0 \sağ)
= dak sol( 0.7 + 0.3 \kez kaldı( \çatlamak{75 \, \Metin{mm}}{2 \zamanlar 75 \, \Metin{mm}} \sağ), 1 \sağ)
= 0.85
\)
Ek olarak, Grup etkisi için faktörler ve eksantrikliğin etkisini faktörler aşağıdaki gibidir.:
\(
\Psi_{g,NB} = 1
\)
\(
\Psi_{ec,N} = 1
\)
En sonunda, referans olarak GİBİ 5216:2021 Eşitlik. 6.2.7 Başlı Ankraj Çubukları için, NS Tasarım Beton patlama direnci dır-dir:
\(
N_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = frac{N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} \ayrıldı( \çatlamak{bir_{Nc}}{A0_{c,NB}} \sağ) \ayrıldı( \Psi_{s,NB} \sağ) \ayrıldı( \Psi_{g,NB} \sağ) \ayrıldı( \Psi_{ec,N} \sağ)}{\gama_{= c times A_}}
\)
\(
N_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = frac{169.97 \, \Metin{kN} \kez kaldı( \çatlamak{45000 \, \Metin{mm}^ 2}{90000 \, \Metin{mm}^ 2} \sağ) \kez kaldı( 0.85 \sağ) \kez kaldı( 1 \sağ) \kez kaldı( 1 \sağ)}{1.5} = 48.159 \, \Metin{kN}
\)
Hatırlamak Ankraj başına gerilim yükü:
\(
N_{Ed} = frac{N_x}{N_{a,t}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Dan beri 12.5 kN < 48.159 kN, Y yönü boyunca beton yan yüz patlaması yeterli.
Başka herhangi bir çapa kimliği numarası da kullanılabilir ve aynı sonucu verir, Tasarım simetrik olduğu için.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #7: Z yönünde yan yüz patlama kapasitesini hesaplayın

Z yönündeki yan yüzlü patlama kapasitesinin hesaplanmasında aynı prosedür kullanılır. Ankraj kimliğini düşünelim #2 bu sefer. Tekrar, Kenar mesafesini hesaplayarak başlıyoruz. başarısızlık kenarı.
\(
c_{Y,\Metin{min}} = dak sol( c_{\Metin{üst},kip-ft}, c_{\Metin{alt},kip-ft} \sağ)
= dak sol( 75 \, \Metin{mm}, 425 \, \Metin{mm} \sağ)
= 75 \, \Metin{mm}
\)
Sonraki, Kenar mesafesini belirliyoruz dik uç.
\(
c_{ile,\Metin{min}} = dak sol( c_{\Metin{ayrıldı},kip-ft}, c_{\Metin{sağ},kip-ft} \sağ)
= dak sol( 75 \, \Metin{mm}, 425 \, \Metin{mm} \sağ)
= 75 \, \Metin{mm}
\)
kullanma İÇİNDE 1992-4:2018 Eşitlik. 7.27, Hadi hesaplayalım Referans Yansıtılan Alan tek bir bağlantı elemanı.
\(
A0_{c,NB} = sol( 4 c_{Y,\Metin{min}} \sağ)^ 2
= sol( 4 \zamanlar 75 \, \Metin{mm} \sağ)^ 2
= 90000 \, \Metin{mm}^ 2
\)
Çapa grubunun kapasitesini kontrol ettiğimiz için, Hadi alalım Gerçek öngörülen alan Çapa grubunun İÇİNDE 1992-4:2018 Eşitlik. 7.27.
\(
bir_{Nc} = B_{c,NB} H_{c,NB}
= 225 \, \Metin{mm} \zamanlar 200 \, \Metin{mm}
= 45000 \, \Metin{mm}^ 2
\)
Nerede,
\(
B_{c,NB} = 2 c_{Y,\Metin{min}} + \Min Sol( 2 c_{Y,\Metin{min}}, c_{ile,\Metin{min}} \sağ)
= 2 \zamanlar 75 \, \Metin{mm} + \Min Sol( 2 \zamanlar 75 \, \Metin{mm}, 75 \, \Metin{mm} \sağ)
= 225 \, \Metin{mm}
\)
\(
H_{c,NB} = 2 c_{Y,\Metin{min}} + \ayrıldı( \Min Sol( t_{\Metin{conc}} – h_{\Metin{ef}}, 2 c_{Y,\Metin{min}} \sağ) \sağ)
= 2 \zamanlar 75 \, \Metin{mm} + \ayrıldı( \Min Sol( 350 \, \Metin{mm} – 300 \, \Metin{mm}, 2 \zamanlar 75 \, \Metin{mm} \sağ) \sağ)
= 200 \, \Metin{mm}
\)
Hesaplamada karakteristik beton patlama gücü bireysel bir çapa, kullanacağız İÇİNDE 1992-4:2018 Eşitlik. 7.26.
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = k_5 ( \çatlamak{c_{Y,\Metin{min}}}{\Metin{mm}} \sağ)
\sqrt{\ayrıldı( \çatlamak{bir_{brg}}{\Metin{mm}^ 2} \sağ)}
\sqrt{\ayrıldı( \çatlamak{f_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}}{\Metin{MPa}} \sağ)} \, \Metin{N}
\)
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = 8.7 \ayrıldı( \çatlamak{75 \, \Metin{mm}}{1 \, \Metin{mm}} \sağ)
\sqrt{\ayrıldı( \çatlamak{2714.3 \, \Metin{mm}^ 2}{1 \, \Metin{mm}^ 2} \sağ)}
\sqrt{\ayrıldı( \çatlamak{25 \, \Metin{MPa}}{1 \, \Metin{MPa}} \sağ)}
\cdot 0.001 \, \Metin{kN}
\)
\(
N0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,cb} = 169.97 \, \Metin{kN}
\)
Sonra, Biz alacağız Yan yüzlü patlama parametreleri.
Streslerin betondaki dağılımının bozulmasının muhasebesi parametre hesaplanabilir. İÇİNDE 1992-4:2018 Eşitlik. 7.28.
\(
\Psi_{s,NB} = dak sol( 0.7 + 0.3 \ayrıldı( \çatlamak{c_{ile,\Metin{min}}}{2 c_{Y,\Metin{min}}} \sağ), 1.0 \sağ)
= dak sol( 0.7 + 0.3 \kez kaldı( \çatlamak{75 \, \Metin{mm}}{2 \zamanlar 75 \, \Metin{mm}} \sağ), 1 \sağ)
= 0.85
\)
Ek olarak, Grup etkisi için faktörler ve eksantrikliğin etkisini faktörler aşağıdaki gibidir.:
\(
\Psi_{g,NB} = 1
\)
\(
\Psi_{ec,N} = 1
\)
En sonunda, referans olarak GİBİ 5216:2021 Eşitlik. 6.2.7 Başlı Ankraj Çubukları için, NS Tasarım Beton patlama direnci dır-dir:
Hatırlamak Ankraj başına gerilim yükü:
\(
N_{Ed} = frac{N_x}{N_{a,t}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Dan beri 12.5 kN < 48.159 kN, Z yönü boyunca beton yan yüz patlaması yeterli.
Başka herhangi bir çapa kimliği numarası da kullanılabilir ve aynı sonucu verir, Tasarım simetrik olduğu için.
Tasarım Özeti
NS Skyciv Base Plaka Tasarım Yazılımı Bu tasarım örneği için otomatik olarak adım adım hesaplama raporu oluşturabilir. Ayrıca gerçekleştirilen kontrollerin ve bunların sonuç oranlarının bir özetini sağlar, Bir bakışta bilginin anlaşılmasını kolaylaştırmak. Aşağıda bir örnek özet tablosu var, rapora dahildir.
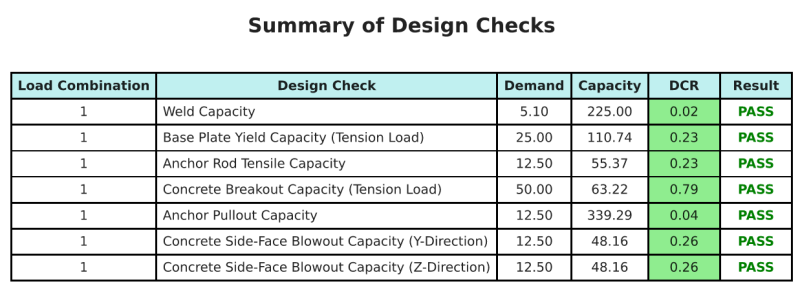
Skyciv Örnek Raporu
SkyCiv Taban Plakası Tasarım Raporundan bekleyebileceğiniz ayrıntı ve netlik düzeyini görün. Rapor tüm önemli tasarım kontrollerini içerir, denklemler, ve sonuçların net ve okunması kolay bir formatta sunulması. Tasarım standartlarıyla tam uyumludur. SkyCiv Taban Plakası Hesaplayıcısı kullanılarak oluşturulan örnek raporu görüntülemek için aşağıya tıklayın.
Base Plaka Yazılımı Satın Alın
Base Plaka Tasarım Modülünün tam sürümünü başka bir SkyCiv modül olmadan kendi başına satın alın. Bu size taban plakası tasarımı için tam bir dizi sonuç verir, ayrıntılı raporlar ve daha fazla işlevsellik dahil.