CSA S16 kullanarak taban plaka tasarımı örneği:19 ve CSA A23.3:19
Sorun Bildirimi:
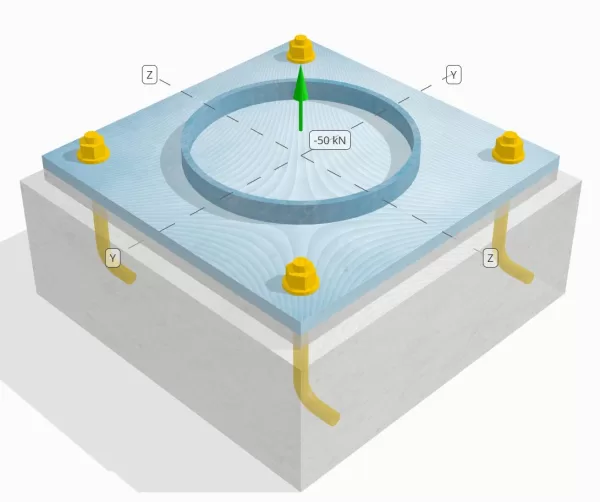
50 kn gerilimli bir yük için tasarlanmış sütun-taban plakası bağlantısının yeterli olup olmadığını belirleyin.
Verilen Veriler:
Sütun:
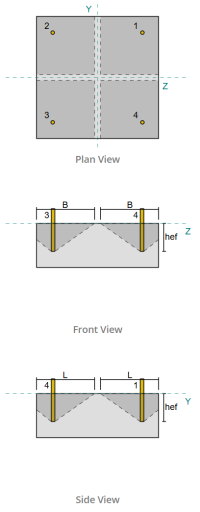
Sütun bölümü: Hs324x9.5
Sütun alanı: 9410 mm2
Sütun malzemesi: 230G
Taban plakası:
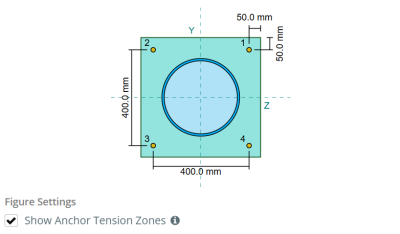
Taban plaka boyutları: 500 mm x 500 mm
Taban plakası kalınlığı: 20 mm
Taban plaka malzemesi: 230G
Izgara:
Grout kalınlığı: 20 mm
Somut:
Somut boyutlar: 550 mm x 550 mm
Beton kalınlığı: 200 mm
Beton malzeme: 20.68 MPa
Çatlamış veya çatlaksız: Çatlak
Çapa:
Çapa: 19.1 mm
Etkili gömme uzunluğu: 130.0 mm
Kanca uzunluğu: 60mm
Çapa ofseti sütunun yüzünden mesafe: 120.84 mm
Kaynaklar:
Kaynak tipi: CJP
Dolgu Metal Sınıflandırması: E43xx
Çapa Verileri (itibaren SkyCiv Hesap Makinesi):
Tanımlar:
Yük yolu:
Bir taban plakası yükselmeye tabi tutulduğunda (çekme) kuvvetler, Bu kuvvetler ankraj çubuklarına aktarılır, bu da taban plakadaki bükülme momentlerini indükler. Bükme eylemi şöyle görülebilir. konsol bükme sütun bölümünün flanşlarının veya ağının etrafında meydana gelir, Ankrajların nerede konumlandırıldığına bağlı olarak.
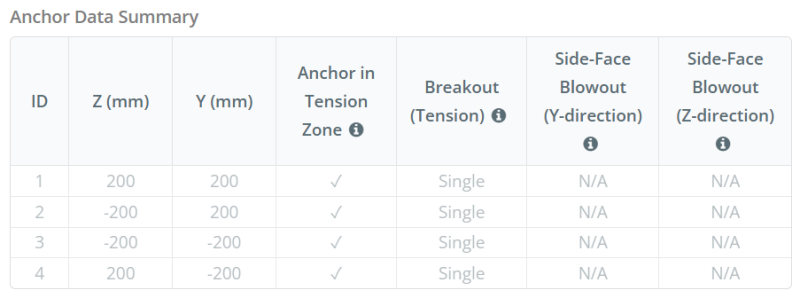
İçinde SkyCiv Taban Plakası Tasarım Yazılımı, sadece içinde bulunan ankrajlar çapa gerilim bölgesi yükselişe direnmede etkili kabul edilir. Bu bölge tipik olarak sütun flanşlarının veya web'in yakınındaki alanları içerir. Bir durumunda dairesel sütun, Ankraj gerginliği bölgesi, sütun çevresinin dışındaki tüm alanı içerir. Bu bölgenin dışındaki ankrajlar gerilim direncine katkıda bulunmaz ve yükselme hesaplamalarından hariç tutulur.
Bükülmeye direnen taban plakasının etkili alanını belirlemek için, a 45-derece dispersiyon her çapa çubuğunun merkez çizgisinden sütun yüzüne doğru varsayılır. Bu dağılım, Etkili kaynak uzunluğu ve kurulmaya yardımcı olur Etkili bükülme genişliği plakanın.
Varsayım, yükselme kuvvetinin plakadan nasıl yayıldığını tahmin ederek taban plakası analizini basitleştirir..
Çapa:
NS SkyCiv Taban Plakası Tasarım Yazılımı Hangi çapaların değerlendirmek için bir çapa grubunun parçası olduğunu belirleyen sezgisel bir özellik içerir. beton patlaması ve beton yan yüzlü patlama başarısızlık.
Bir çapa Benzer etkili gömme derinlikleri ve aralıklı çoklu ankrajlardan oluşur, ve onların Öngörülen direnç alanları örtüşüyor. Çapalar gruplandığında, Gruba uygulanan toplam gerilim kuvvetine direnmek için kapasiteleri birleştirilir.
Gruplama kriterlerini karşılamayan çapalar, tek çapa. Bu durumda, Sadece bireysel çapa üzerindeki gerilim kuvveti kendi etkili direnç alanına göre kontrol edilir.
Adım adım hesaplamalar:
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #1: Kaynak kapasitesini hesapla
Başlamak, Ankraj başına yükü hesaplamamız ve her bir çapa için etkili kaynak uzunluğunu belirlememiz gerekir.. NS Etkili kaynak uzunluğu bir 45° dispersiyon hattı çapanın merkezinden sütunun yüzüne çizilmiş. Bu 45 ° hat sütunla kesişmiyorsa, NS Teğet Noktalar bunun yerine kullanılır. bunlara ek olarak, Çapalar yakın aralıktıysa, Çakışmayı önlemek için etkili kaynak uzunluğu azalır. En sonunda, Tüm etkili kaynak uzunluklarının toplamı, sütun çevresi boyunca mevcut olan gerçek kaynaklı uzunluğu aşmamalıdır.
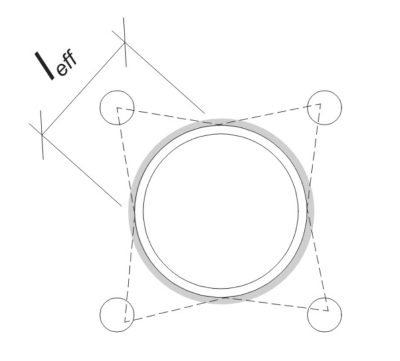
Bunu örneğimize uygulayalım. Verilen geometriye dayanarak, Ankrajdan 45 ° çizgi, sütunla kesişmez. Sonuç olarak, bunun yerine teğet noktalar arasındaki ark uzunluğu kullanılır. Bu ark uzunluğu, bitişik ankrajları da açıklamalıdır., Çift sayımdan kaçınmak için örtüşen kısımlar çıkarıldı. Hesaplanan ark uzunluğu:
\(
l_{\Metin{yay}} = 254.47 \, \Metin{mm}
\)
Bu ark uzunluğu hesaplaması SkyCiv Base Plaka Tasarım Yazılımında tamamen otomatiktir., ancak trigonometrik yöntemler kullanılarak manuel olarak yapılabilir. Bu bağlantıdan ücretsiz aracı deneyebilirsiniz.
Sütunun çevresi boyunca mevcut kaynaklanabilir uzunluğu göz önünde bulundurarak, final Etkili kaynak uzunluğu dır-dir:
\(
l_{\Metin{eff}} = dak sol( l_{\Metin{yay}}, \çatlamak{\Pi D_{\Metin{seri}}}{N_{a,t}} \sağ) = dak sol( 254.47 \, \Metin{mm}, \çatlamak{\Pi Times 324 \, \Metin{mm}}{4} \sağ) = 254.47 \, \Metin{mm}
\)
Sonraki, Hadi hesaplayalım Ankraj başına yük. Belirli bir dört set için (4) çapalar, Ankraj başına yük:
\(
T_{sen,\Metin{Çapa}} = frac{N_x}{N_{a,t}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Hesaplanan etkili kaynak uzunluğunu kullanarak, Şimdi hesaplayabiliriz Birim uzunluk başına gerekli kuvvet Kaynakta hareket etmek.
\(
v_f = frac{T_{sen,\Metin{Çapa}}}{l_{\Metin{eff}}} = frac{12.5 \, \Metin{kN}}{254.47 \, \Metin{mm}} = 0.049122 \, \Metin{kN/mm}
\)
Şimdi, Bahsediyoruz CSA S16:19 Madde 13.13.3.1 hesaplamak için Tam eklem penetrasyonunun faktored direnci (CJP) kaynak. Bu temel metal direncini gerektirir, birim uzunluk başına yürürlükte ifade edildi, hem sütun hem de taban plaka malzemeleri için.
\(
v_{r,\Metin{BM}} = Phi Sol( \Min Sol( F_{Y,\Metin{seri}} t_{\Metin{seri}}, F_{Y,\Metin{bp}} t_{\Metin{bp}} \sağ) \sağ)
\)
\(
v_{r,\Metin{BM}} = 0.9 \kez kaldı( \Min Sol( 230 \, \Metin{MPa} \zamanlar 9.53 \, \Metin{mm}, 230 \, \Metin{MPa} \zamanlar 20 \, \Metin{mm} \sağ) \sağ) = 1.9727 \, \Metin{kN/mm}
\)
Dan beri 0.049122 kN/mm < 1.9727 kN/mm, Kaynak kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #2: Gerginlik yükü nedeniyle taban plakası eğilme verme kapasitesini hesaplayın
Ankraj başına yükü kullanmak ve ofset mesafesi çapanın merkezinden sütunun yüzüne kadar, Taban plakasına uygulanan an bir konsol varsayım. Dairesel bir sütun için, Yük eksantrikliği, kaynaklı arkın sagitası dikkate alınarak belirlenir, ve aşağıdaki gibi hesaplanabilir:
\(
e_{\Metin{boru}} = d_o + r_{\Metin{seri}} \ayrıldı( 1 – \çünkü sol( \çatlamak{l_{\Metin{eff}}}{2 r_{\Metin{seri}}} \sağ) \sağ)
\)
\(
e_{\Metin{boru}} = 120.84 \, \Metin{mm} + 162 \, \Metin{mm} \kez kaldı( 1 – \çünkü sol( \çatlamak{254.47 \, \Metin{mm}}{2 \zamanlar 162 \, \Metin{mm}} \sağ) \sağ) = 168.29 \, \Metin{mm}
\)
İndüklenen an olarak hesaplanır:
\(
M_f = t_{sen,\Metin{Çapa}} e_{\Metin{boru}} = 12.5 \, \Metin{kN} \zamanlar 168.29 \, \Metin{mm} = 2103.6 \, \Metin{kN} \cdot metin{mm}
\)
Sonraki, Taban plakasının bükülme genişliğini belirleyeceğiz. Bunun için, Kullanıyoruz akor uzunluğu etkili kaynak arkına karşılık gelir.
\(
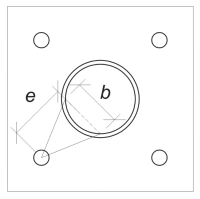
\teta_{\Metin{rad}} = frac{l_{\Metin{eff}}}{0.5 d_{\Metin{seri}}} = frac{254.47 \, \Metin{mm}}{0.5 \zamanlar 324 \, \Metin{mm}} = 1.5708
\)
\(
b = d_{\Metin{seri}} \ayrıldı( \günah sol( \çatlamak{\teta_{\Metin{rad}}}{2} \sağ) \sağ) = 324 \, \Metin{mm} \kez kaldı( \günah sol( \çatlamak{1.5708}{2} \sağ) \sağ) = 229.1 \, \Metin{mm}
\)
En sonunda, hesaplayabiliriz faktörlü bükülme direnci taban plakasının CSA S16:19 Madde 13.5.
\(
M_r = Phi f_{Y,\Metin{bp}} Z_{\Metin{eff}} = 0.9 \zamanlar 230 \, \Metin{MPa} \zamanlar 22910 \, \Metin{mm}^3 = 4742.4 \, \Metin{kN} \cdot metin{mm}
\)
Nerede,
\(
Z_{\Metin{eff}} = frac{b (t_{\Metin{bp}})^ 2}{4} = frac{229.1 \, \Metin{mm} \zamanlar (20 \, \Metin{mm})^ 2}{4} = 22910 \, \Metin{mm}^3
\)
Dan beri 2103.6 KN-MM < 4742.4 KN-MM, taban plakası bükülme verim kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #3: Ankraj çubuğu gerilme kapasitesini hesaplayın
Ankraj çubuğunun gerilme kapasitesini değerlendirmek için, CSA A23.3'ten bahsediyoruz:19 D.6.1.2 ve CSA S16:19 Madde 25.3.2.1.
İlk, Belirliyoruz Belirtilen gerilme mukavemeti Çapa çeliğinin. Bu, izin verilen en düşük değerdir CSA A23.3:19 Madde D.6.1.2.
\(
f_{\Metin{uta}} = dak sol( F_{sen,\Metin{anc}}, 1.9 F_{Y,\Metin{anc}}, 860 \sağ) = dak sol( 400 \, \Metin{MPa}, 1.9 \zamanlar 248.2 \, \Metin{MPa}, 860.00 \, \Metin{MPa} \sağ) = 400 \, \Metin{MPa}
\)
Sonraki, Belirliyoruz Etkili kesit alanı gerginlikteki ankraj çubuğunun CAC Beton Tasarım El Kitabı, 3Rd Edition, Tablo 12.3.
\(
bir_{biliyorum,N} = 215 \, \Metin{mm}^ 2
\)
Bu değerlerle, uyguluyoruz CSA A23.3:19 Eşitlik. D.2 hesaplamak için faktörlü gerilme direnci ankraj çubuğunun.
\(
N_{\Metin{SAR}} = A_{biliyorum,N} \phi_s f_{\Metin{uta}} R = 215 \, \Metin{mm}^2 Times 0.85 \zamanlar 400 \, \Metin{MPa} \zamanlar 0.8 = 58.465 \, \Metin{kN}
\)
bunlara ek olarak, değerlendiriyoruz faktörlü gerilme direnci buna göre CSA S16:19 Madde 25.3.2.1.
\(
T_r = phi_{AR} 0.85 bir_{AR} F_{sen,\Metin{anc}} = 0.67 \zamanlar 0.85 \zamanlar 285.02 \, \Metin{mm}^2 Times 400 \, \Metin{MPa} = 64.912 \, \Metin{kN}
\)
İkisini karşılaştırdıktan sonra, CSA A23.3 kullanılarak hesaplanan faktör direncinin:19 Bu durumda yönetir.
Daha önce hesaplananları hatırlayın Ankraj başına gerilim yükü:
\(
N_{FA} = frac{N_x}{N_{a,t}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Dan beri 12.5 kN < 58.465 kN, Ankraj çubuğu gerilme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #4: Gerginlikte beton kırılma kapasitesini hesaplayın
Kırılma kapasitesini hesaplamadan önce, Öncelikle üyenin bir dar üye. Göre CSA A23.3:19 Madde D.6.2.3, Üye, dar bir üye için kriterleri karşılamıyor. Bu nedenle, verilen Etkili gömme uzunluğu hesaplamalarda kullanılacak.
kullanma CSA A23.3:19 Eşitlik. D.5, hesaplıyoruz maksimum yansıtılan beton koni alanı tek bir çapa için, Etkili gömme uzunluğuna göre.
\(
bir_{Hatırlamak} = 9 (h_{ef,kip-ft})montaj yüksekliğinde 9 \zamanlar (130 \, \Metin{mm})montaj yüksekliğinde 152100 \, \Metin{mm}^ 2
\)
benzer şekilde, Hesaplamak için etkili gömme uzunluğunu kullanıyoruz. gerçek öngörülen beton koni alanı tek çapa.
\(
bir_{Nc} = L_{Nc} B_{Nc} = 270 \, \Metin{mm} \zamanlar 270 \, \Metin{mm} = 72900 \, \Metin{mm}^ 2
\)
Nerede,
\(
L_{Nc} = sol( \Min Sol( c_{\Metin{ayrıldı},kip-ft}, 1.5 h_{ef,kip-ft} \sağ) \sağ) + \ayrıldı( \Min Sol( c_{\Metin{sağ},kip-ft}, 1.5 h_{ef,kip-ft} \sağ) \sağ)
\)
\(
L_{Nc} = sol( \Min Sol( 475 \, \Metin{mm}, 1.5 \zamanlar 130 \, \Metin{mm} \sağ) \sağ) + \ayrıldı( \Min Sol( 75 \, \Metin{mm}, 1.5 \zamanlar 130 \, \Metin{mm} \sağ) \sağ)
\)
\(
L_{Nc} = 270 \, \Metin{mm}
\)
\(
B_{Nc} = sol( \Min Sol( c_{\Metin{üst},kip-ft}, 1.5 h_{ef,kip-ft} \sağ) \sağ) + \ayrıldı( \Min Sol( c_{\Metin{alt},kip-ft}, 1.5 h_{ef,kip-ft} \sağ) \sağ)
\)
\(
B_{Nc} = sol( \Min Sol( 75 \, \Metin{mm}, 1.5 \zamanlar 130 \, \Metin{mm} \sağ) \sağ) + \ayrıldı( \Min Sol( 475 \, \Metin{mm}, 1.5 \zamanlar 130 \, \Metin{mm} \sağ) \sağ)
\)
\(
B_{Nc} = 270 \, \Metin{mm}
\)
Sonraki, değerlendiriyoruz faktörlü Temel beton kırılma direnci kullanan tek bir çapanın CSA A23.3:19 Eşitlik. D.6
\(
N_{br} = k_c Phi lambda_a sqrt{\çatlamak{f'_c}{\Metin{MPa}}} \ayrıldı( \çatlamak{h_{ef,kip-ft}}{\Metin{mm}} \sağ)^{1.5} RN
\)
\(
N_{br} = 10 \zamanlar 0.65 \zamanlar 1 \kez sqrt{\çatlamak{20.68 \, \Metin{MPa}}{1 \, \Metin{MPa}}} \kez kaldı( \çatlamak{130 \, \Metin{mm}}{1 \, \Metin{mm}} \sağ)^{1.5} \zamanlar 1 \zamanlar 0.001 \, \Metin{kN} = 43.813 \, \Metin{kN}
\)
Nerede,
- \(Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{c} = 10\) dökme ankrajlar için
- \(\Lambda = 1.0 \) Normal ağırlıklı beton için
Şimdi, Geometrinin etkilerini hesaplayarak değerlendiriyoruz. kenar etki faktörü.
Çapa grubunun en kısa kenar mesafesi olarak belirlenir.:
\(
c_{a,\Metin{min}} = dak sol( c_{\Metin{ayrıldı},kip-ft}, c_{\Metin{sağ},kip-ft}, c_{\Metin{üst},kip-ft}, c_{\Metin{alt},kip-ft} \sağ) = dak sol( 475 \, \Metin{mm}, 75 \, \Metin{mm}, 75 \, \Metin{mm}, 475 \, \Metin{mm} \sağ) = 75 \, \Metin{mm}
\)
Göre CSA A23.3:19 Eşitlik. D.10 ve D.11, Breakout kenar etki faktörü dır-dir:
\(
\Psi_{ed,N} = dak sol( 1.0, 0.7 + 0.3 \ayrıldı( \çatlamak{c_{a,\Metin{min}}}{1.5 h_{ef,kip-ft}} \sağ) \sağ) = dak sol( 1, 0.7 + 0.3 \kez kaldı( \çatlamak{75 \, \Metin{mm}}{1.5 \zamanlar 130 \, \Metin{mm}} \sağ) \sağ) = 0.81538
\)
Ek olarak, her ikisi de çatlak faktörü ve bölme faktörü olarak alınır:
\(
\Psi_{c,N} = 1
\)
\(
\Psi_{cp,N} = 1
\)
Sonra, Tüm bu faktörleri birleştiriyoruz ve kullanıyoruz ACI 318-19 Eşitlik. 17.6.2.1b değerlendirmek için faktörlü beton kırılma direnci tek çapa:
\(
N_{CBR} = sol( \çatlamak{bir_{Nc}}{bir_{Hatırlamak}} \sağ) \Psi_{ed,N} \Psi_{c,N} \Psi_{cp,N} N_{br} = sol( \çatlamak{72900 \, \Metin{mm}^ 2}{152100 \, \Metin{mm}^ 2} \sağ) \zamanlar 0.81538 \zamanlar 1 \zamanlar 1 \zamanlar 43.813 \, \Metin{kN} = 17.122 \, \Metin{kN}
\)
Daha önce hesaplananları hatırlayın Ankraj başına gerilim yükü:
\(
N_{FA} = frac{N_x}{N_{a,s}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Dan beri 12.5 kN < 17.122 kN Beton kırılma kapasitesi yeterli.
Bu somut koparma hesaplaması, ankraj kimliğine dayanmaktadır #1. Simetrik tasarım nedeniyle diğer ankrajlar için aynı kapasite uygulanacaktır.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #5: Çapa çekme kapasitesini hesaplayın
Bir çapanın çekilme kapasitesi, gömülü ucundaki direnç tarafından yönetilir. Bağlı çapalar için, kanca uzunluğuna bağlıdır.
Hesaplıyoruz Factored temel çapa çekme direnci başına CSA A23.3:19 Eşitlik. D.17.
\(
N_{PR} = Psi_{c,p} 0.9 \fi (f'_c) E_H D_A R = 1 \zamanlar 0.9 \zamanlar 0.65 \zamanlar (20.68 \, \Metin{MPa}) \zamanlar 60 \, \Metin{mm} \zamanlar 19.05 \, \Metin{mm} \zamanlar 1 = 13.828 \, \Metin{kN}
\)
Daha önce hesaplananları hatırlayın Ankraj başına gerilim yükü:
\(
N_{FA} = frac{N_x}{N_{a,t}} = frac{50 \, \Metin{kN}}{4} = 12.5 \, \Metin{kN}
\)
Dan beri 12.5 kN < 13.828 kN, Çapa çekme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #6: Y yönünde yan yüz patlama kapasitesini hesaplayın
Bu hesaplama, kancalı ankrajlar için geçerli değildir.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #7: Z yönünde yan yüz patlama kapasitesini hesaplayın
Bu hesaplama, kancalı ankrajlar için geçerli değildir.
Tasarım Özeti
NS Skyciv Base Plaka Tasarım Yazılımı Bu tasarım örneği için otomatik olarak adım adım hesaplama raporu oluşturabilir. Ayrıca gerçekleştirilen kontrollerin ve bunların sonuç oranlarının bir özetini sağlar, Bir bakışta bilginin anlaşılmasını kolaylaştırmak. Aşağıda bir örnek özet tablosu var, rapora dahildir.
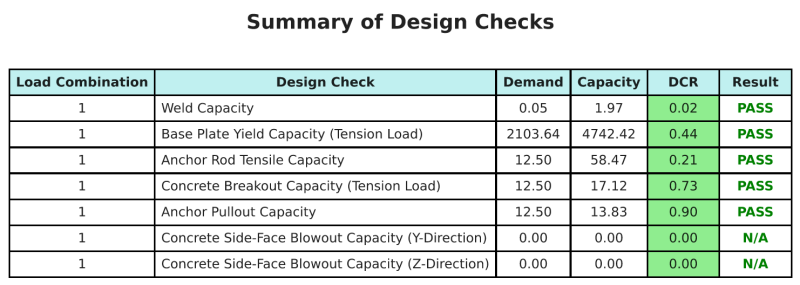
Skyciv Örnek Raporu
Örnek rapor yakında eklenecek.
Base Plaka Yazılımı Satın Alın
Diğer Skyciv modülleri olmadan temel plaka tasarım modülü onits'in tam sürümünü satın alın. Bu size taban plakası tasarımı için tam bir dizi sonuç verir, ayrıntılı raporlar ve daha fazla işlevsellik dahil.
