AISC Kullanarak Base Plaka Tasarım Örneği 360-22 ve ACI 318-19
Sorun Bildirimi
20 kip gerginlik yükü için tasarlanmış sütun-baz plaka bağlantısının yeterli olup olmadığını belirleyin.
Verilen Veriler
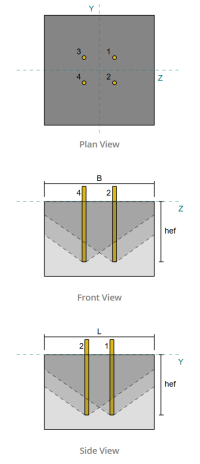
Sütun:
Sütun bölümü: W12x53
Sütun alanı: 15.6 içinde2
Sütun malzemesi: A992
Taban plakası:
Taban plaka boyutları: 18 x içinde 18 içinde
Taban plakası kalınlığı: 3/4 içinde
Taban plaka malzemesi: A36
Izgara:
Grout kalınlığı: 1 içinde
Somut:
Somut boyutlar: 22 x içinde 22 içinde
Beton kalınlığı: 15 içinde
Beton malzeme: 4000 psi
Çatlamış veya çatlaksız: Çatlak
Çapa:
Çapa: 3/4 içinde
Etkili gömme uzunluğu: 12 içinde
Gömülü plaka genişliği: 3 içinde
Gömülü plaka kalınlığı: 1/4 içinde
Sütun ağının yüzünden ankraj ofset mesafesi: 2.8275 içinde
Kaynaklar:
kaynak boyutu: 1/4 içinde
Dolgu Metal Sınıflandırması: E70XX
Çapa Verileri (itibaren SkyCiv Hesap Makinesi):
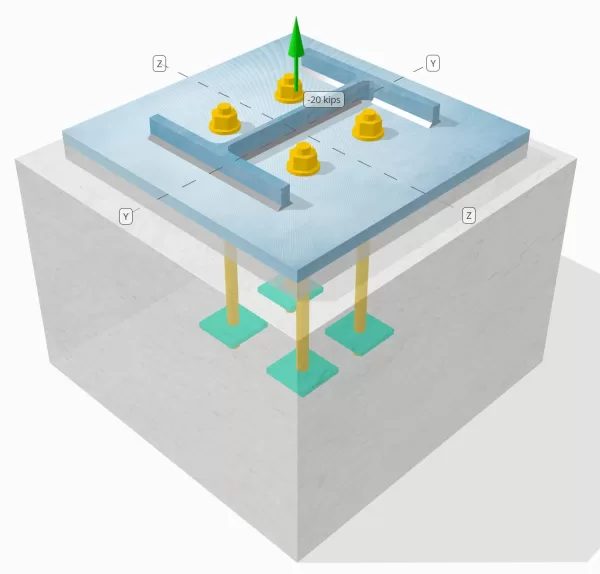
SkyCiv Ücretsiz Aracındaki Model
Ücretsiz çevrimiçi aracımızı kullanarak yukarıdaki taban plakası tasarımını bugün modelleyin! Kayıt olmanıza gerek yok.
Tanımlar
Yük yolu:
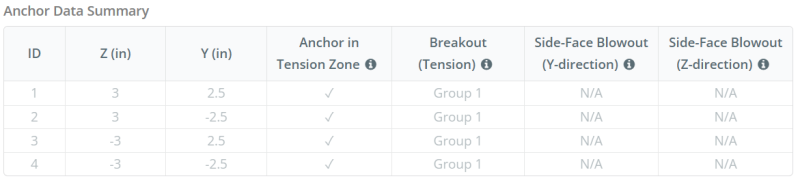
Bir taban plakası yükselmeye tabi tutulduğunda (çekme) kuvvetler, Bu kuvvetler ankraj çubuklarına aktarılır, bu da taban plakadaki bükülme momentlerini indükler. Bükme eylemi şöyle görülebilir. konsol bükme sütun bölümünün flanşlarının veya ağının etrafında meydana gelir, Ankrajların nerede konumlandırıldığına bağlı olarak.
İçinde SkyCiv Taban Plakası Tasarım Yazılımı, sadece içinde bulunan ankrajlar çapa gerilim bölgesi yükselişe direnmede etkili kabul edilir. Bu bölge tipik olarak sütun flanşlarının veya web'in yakınındaki alanları içerir. Bu bölgenin dışındaki ankrajlar gerilim direncine katkıda bulunmaz ve yükselme hesaplamalarından hariç tutulur.
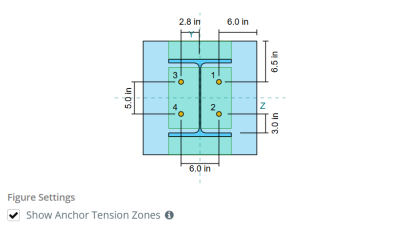
Bükülmeye direnen taban plakasının etkili alanını belirlemek için, a 45-derece dispersiyon her çapa çubuğunun merkez çizgisinden sütun yüzüne doğru varsayılır. Bu dağılım, Etkili kaynak uzunluğu ve kurulmaya yardımcı olur Etkili bükülme genişliği plakanın.
Varsayım, yükselme kuvvetinin plakadan nasıl yayıldığını tahmin ederek taban plakası analizini basitleştirir..
Çapa:
NS SkyCiv Taban Plakası Tasarım Yazılımı Hangi çapaların değerlendirmek için bir çapa grubunun parçası olduğunu belirleyen sezgisel bir özellik içerir. beton patlaması ve Beton SidE-yüz patlama başarısızlık.
Bir çapa Benzer etkili gömme derinlikleri ve aralıklı çoklu ankrajlardan oluşur, ve onların Öngörülen direnç alanları örtüşüyor. Çapalar gruplandığında, Gruba uygulanan toplam gerilim kuvvetine direnmek için kapasiteleri birleştirilir.
Gruplama kriterlerini karşılamayan çapalar, tek çapa. Bu durumda, Sadece bireysel çapa üzerindeki gerilim kuvveti kendi etkili direnç alanına göre kontrol edilir.
Adım adım hesaplamalar
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #1: Kaynak kapasitesini hesapla
Başlamak, Ankraj başına yükü ve ankraj başına etkili kaynak uzunluğunu hesaplamamız gerekiyor. Etkili kaynak uzunluğu, en kısa uzunlukta belirlenir. 45° Dispersiyon, gerçek kaynak uzunluğu ve ankraj aralığı ile kısıtlanmıştır.
Bu hesaplama için, çapalar ya olarak sınıflandırılır son çapa veya ara ankraj. Uç ankrajlar, bir satırın uçlarında veya çapa sütununda bulunur, ara ankrajlar aralarında konumlandırılır. Hesaplama yöntemi her biri için farklılık gösterir ve sütun geometrisine bağlıdır. Bu örnekte, Web boyunca iki çapa var, ve her ikisi de uç ankraj olarak sınıflandırılır.
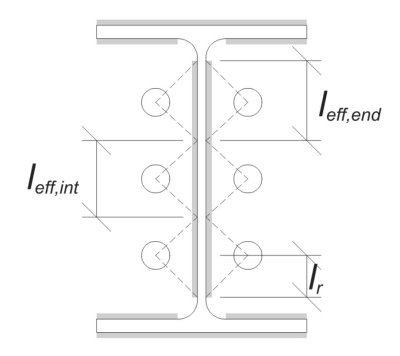
Uç Ankrajlar için, Etkili kaynak uzunluğu, ankraj merkez çizgisinden sütun filetosuna mevcut mesafe ile sınırlıdır.. 45 ° dispersiyon bu sınırın ötesine geçmemelidir.
\(
l_r = frac{d_{seri} – 2T_F – 2r_{seri} – S_(N_{a,taraf} – 1)}{2} = frac{12.1 \, \Metin{içinde} – 2 \zamanlar 0.575 \, \Metin{içinde} – 2 \zamanlar 0.605 \, \Metin{içinde} – 5 \, \Metin{içinde} \zamanlar (2 – 1)}{2} = 2.37 \, \Metin{içinde}
\)
İç tarafta, Etkili uzunluk, ankraj aralığının yarısı ile sınırlıdır. Uç ankrajı için toplam etkili kaynak uzunluğu, dış ve iç uzunlukların toplamıdır.
\(
l_{eff,son} = min(Yapmak, 0.5S_) + \min(Yapmak, l_r)
\)
\(
l_{eff,son} = min(2.8275 \, \Metin{içinde}, 0.5 \zamanlar 5 \, \Metin{içinde}) + \min(2.8275 \, \Metin{içinde}, 2.37 \, \Metin{içinde}) = 4.87 \, \Metin{içinde}
\)
Bu örnek için, NS Son etkili kaynak uzunluğu Web çapası için son çapanın etkili uzunluğu olarak alınır.
\(
l_{eff} = l_{eff,son} = 4.87 \, \Metin{içinde}
\)
Sonraki, Hadi hesaplayalım Ankraj başına yük. Belirli bir dört set için (4) çapalar, Ankraj başına yük:
\(
T_{sen,Çapa} = frac{N_x}{N_{a,t}} = frac{20 \, \Metin{kip}}{4} = 5 \, \Metin{kip}
\)
Hesaplanan etkili kaynak uzunluğunu kullanarak, Şimdi belirleyebiliriz Kaynak üzerindeki birim uzunluk başına gerekli kuvvet.
\(
r_u = frac{T_{sen,Çapa}}{l_{eff}} = frac{5 \, \Metin{kip}}{4.87 \, \Metin{içinde}} = 1.0267 \, \Metin{Kip/in}
\)
Şimdi, kullanacağız AISC 360-22, Bölüm J2.4 Fileto kaynağının tasarım gücünü hesaplamak için.
Uygulanan yük tamamen eksenel gerilim olduğundan, açı \(\teta) 90 ° olarak alınır, ve yönlü mukavemet katsayısı KDS AISC 360-22 Eşitlik. J2-5.
\(
Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{ds} = 1.0 + 0.5(\olmadan(\teta))^{1.5} = 1 + 0.5 \zamanlar (\olmadan(1.5708))^{1.5} = 1.5
\)
En sonunda, başvuracağız AISC 360-22 Eşitlik. J2-4 belirlemek için Birim uzunluk başına fileto kaynağının tasarım gücü.
\(
\Phi r_n = Phi 0.6 F_{EXX} E_{w,ağ} Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{ds} = 0.75 \zamanlar 0.6 \zamanlar 70 \, \Metin{ksi} \zamanlar 0.177 \, \Metin{içinde} \zamanlar 1.5 = 8.3633 \, \Metin{Kip/in}
\)
Dan beri 1.0267 KPI < 8.3633 KPI, Kaynak kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #2: Gerginlik yükü nedeniyle taban plakası eğilme verme kapasitesini hesaplayın
T kullanmaAnkraj başına yük ve oFFSET Ankrajın merkezinden sütunun yüzüne mesafe (yük eksantrikliği olarak hizmet etmek), Taban plakasına uygulanan an bir konsol varsayım.
\(
M_U = T_{sen,\Metin{Çapa}} e = 5 \, \Metin{kip} \zamanlar 2.8275 \, \Metin{içinde} = 14.137 \, \Metin{kip} \cdot metin{içinde}
\)
Sonraki, Hesaplama kullanarakD Etkili kaynak uzunluğum bükme genişliği olarak önceki kontrol, hesaplayabiliriz Taşıma kapasitesini hesaplar taban plakasının AISC 360-22, Denklem 2-1:
\(
\non -m_n = Phi f_{Y,\Metin{bp}} Z_{\Metin{eff}} = 0.9 \zamanlar 36 \, \Metin{ksi} \zamanlar 0.68484 \, \Metin{içinde}^3 = 22.189 \, \Metin{kip} \cdot metin{içinde}
\)
Nerede,
\(
Z_{\Metin{eff}} = frac{l_{\Metin{eff}} (t_{\Metin{bp}})^ 2}{4} = frac{4.87 \, \Metin{içinde} \zamanlar (0.75 \, \Metin{içinde})^ 2}{4} = 0.68484 \, \Metin{içinde}^3
\)
Dan beri 14.137 tavuklu < 22.189 tavuklu, taban plakası bükülme verim kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #3: Ankraj çubuğu gerilme kapasitesini hesaplayın
Ankraj çubuğunun gerilme kapasitesini değerlendirmek için, kullanacağız ACI 318-19 Denklem 17.6.1.2.
İlk, Belirliyoruz Belirtilen gerilme mukavemeti Çapa çeliğinin. Bu, izin verilen en düşük değerdir ACI 318-19 Madde 17.6.1.2, Malzeme özelliklerine referansla AISC 360-22 Tablo J3.2.
\(
f_{\Metin{uta}} = dak sol( 0.75 F_{sen,\Metin{anc}}, 1.9 F_{Y,\Metin{anc}}, 125 \sağ) = dak sol( 0.75 \zamanlar 120 \, \Metin{ksi}, 1.9 \zamanlar 92 \, \Metin{ksi}, 125.00 \, \Metin{ksi} \sağ) = 90 \, \Metin{ksi}
\)
Sonraki, hesaplıyoruz Etkili kesit alanı ankraj çubuğunun. Bu temeldir ACI 318-19 Yorum Maddesi R17.6.1.2, iplik geometrisini açıklayan. İnç başına iplik sayısı alınır ASME B1.1-2019 Tablo 1.
\(
bir_{biliyorum,N} = frac{\pi}{4} \ayrıldı( D_A – \çatlamak{0.9743}{n_t} \sağ)^2 = frac{\pi}{4} \kez kaldı( 0.75 \, \Metin{içinde} – \çatlamak{0.9743}{10 \, \Metin{içinde}^{-1}} \sağ)montaj yüksekliğinde 0.33446 \, \Metin{içinde}^ 2
\)
Bu değerlerle, uyguluyoruz ACI 318-19 Denklem 17.6.1.2 hesaplamak için Tasarım gerilme mukavemeti ankraj çubuğunun.
\(
\phi N_{için} = phi A_{biliyorum,N} f_{\Metin{uta}} = 0.75 \zamanlar 0.33446 \, \Metin{içinde}^2 Times 90 \, \Metin{ksi} = 22.576 \, \Metin{kip}
\)
Daha önce hesaplananları hatırlayın Ankraj başına gerilim yükü:
\(
N_{Yapmak} = frac{N_x}{N_{a,t}} = frac{20 \, \Metin{kip}}{4} = 5 \, \Metin{kip}
\)
Dan beri 5 kip < 22.576 kip, Ankraj çubuğu gerilme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #4: Gerginlikte beton kırılma kapasitesini hesaplayın

Kırılma kapasitesini hesaplamadan önce, Öncelikle üyenin bir dar üye. Göre ACI 318-19 Madde 17.6.2.1.2, Üye, dar bir üye için kriterleri karşılıyor. Bu nedenle, Hesaplamalarda değiştirilmiş etkili bir gömme uzunluğu kullanılmalıdır.
Belirlenir Modifiye Etkili Gömme Uzunluğu, H’ef, çapa grubunun:
\(
H'_{\Metin{ef}} = 5.667 \, \Metin{içinde}
\)
kullanma ACI 318-19 Madde 17.6.2, hesaplıyoruz maksimum yansıtılan beton koni alanı tek bir çapa için, değiştirilmiş etkili gömme uzunluğuna göre.
\(
bir_{N_{ortak}} = 9 \ayrıldı( H'_{ef,G1} \sağ)montaj yüksekliğinde 9 \kez kaldı( 5.6667 \, \Metin{içinde} \sağ)montaj yüksekliğinde 289 \, \Metin{içinde}^ 2
\)
benzer şekilde, hesaplamak için değiştirilmiş etkili gömme uzunluğunu kullanıyoruz. gerçek öngörülen beton koni alanı çapa grubunun.
\(
bir_{N_C} = dak sol( N_{a,G1} bir_{N_{ortak}}, L_{N_C} B_{N_C} \sağ) = dak sol( 4 \zamanlar 289 \, \Metin{içinde}^ 2, 22 \, \Metin{içinde} \zamanlar 22 \, \Metin{içinde} \sağ) = 484 \, \Metin{içinde}^ 2
\)
Nerede,
\(
L_{N_C} = dak sol( c_{\Metin{ayrıldı},G1}, 1.5 H'_{\Metin{ef},G1} \sağ)
+ \ayrıldı( \Min Sol( S_{\Metin{toplam},ile,G1}, 3 H'_{\Metin{ef},G1} \ayrıldı( N_{ile,G1} – 1 \sağ) \sağ) \sağ)
+ \Min Sol( c_{\Metin{sağ},G1}, 1.5 H'_{\Metin{ef},G1} \sağ)
\)
\(
L_{N_C} = dak sol( 8 \, \Metin{içinde}, 1.5 \zamanlar 5.6667 \, \Metin{içinde} \sağ)
+ \ayrıldı( \Min Sol( 6 \, \Metin{içinde}, 3 \zamanlar 5.6667 \, \Metin{içinde} \kez kaldı( 2 – 1 \sağ) \sağ) \sağ)
+ \Min Sol( 8 \, \Metin{içinde}, 1.5 \zamanlar 5.6667 \, \Metin{içinde} \sağ)
\)
\(
L_{N_C} = 22 \, \Metin{içinde}
\)
\(
B_{N_C} = dak sol( c_{\Metin{üst},G1}, 1.5 H'_{\Metin{ef},G1} \sağ)
+ \ayrıldı( \Min Sol( S_{\Metin{toplam},Y,G1}, 3 H'_{\Metin{ef},G1} \ayrıldı( N_{Y,G1} – 1 \sağ) \sağ) \sağ)
+ \Min Sol( c_{\Metin{alt},G1}, 1.5 H'_{\Metin{ef},G1} \sağ)
\)
\(
B_{N_C} = dak sol( 8.5 \, \Metin{içinde}, 1.5 \zamanlar 5.6667 \, \Metin{içinde} \sağ)
+ \ayrıldı( \Min Sol( 5 \, \Metin{içinde}, 3 \zamanlar 5.6667 \, \Metin{içinde} \kez kaldı( 2 – 1 \sağ) \sağ) \sağ)
+ \Min Sol( 8.5 \, \Metin{içinde}, 1.5 \zamanlar 5.6667 \, \Metin{içinde} \sağ)
\)
\(
B_{N_C} = 22 \, \Metin{içinde}
\)
Sonraki, değerlendiriyoruz Temel beton kırılma gücü kullanan tek bir çapanın ACI 318-19 Madde 17.6.2.2.1
\(
N_b = k_c lambda_a sqrt{\çatlamak{f'_c}{\Metin{psi}}} \ayrıldı( \çatlamak{H'_{\Metin{ef},G1}}{\Metin{içinde}} \sağ)^{1.5} \, \Metin{lbf}
\)
\(
N_b = 24 \zamanlar 1 \kez sqrt{\çatlamak{4 \, \Metin{ksi}}{0.001 \, \Metin{ksi}}} \kez kaldı( \çatlamak{5.6667 \, \Metin{içinde}}{1 \, \Metin{içinde}} \sağ)^{1.5} \zamanlar 0.001 \, \Metin{kip} = 20.475 \, \Metin{kip}
\)
Nerede,
- \(Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.{c} = 24\) dökme ankrajlar için
- \(\Lambda = 1.0 \) Normal ağırlıklı beton için
Şimdi, Geometrinin etkilerini hesaplayarak değerlendiriyoruz. kenar etki faktörü ve eksantriklik faktörü.
Çapa grubunun en kısa kenar mesafesi olarak belirlenir.:
\(
c_{a,\Metin{min}} = dak sol( c_{\Metin{ayrıldı},G1}, c_{\Metin{sağ},G1}, c_{\Metin{üst},G1}, c_{\Metin{alt},G1} \sağ)
= dak sol( 8 \, \Metin{içinde}, 8 \, \Metin{içinde}, 8.5 \, \Metin{içinde}, 8.5 \, \Metin{içinde} \sağ) = 8 \, \Metin{içinde}
\)
Göre ACI 318-19 Madde 17.6.2.4.1, Breakout kenar etki faktörü dır-dir:
\(
\Psi_{ed,N} = dak sol( 1.0, 0.7 + 0.3 \ayrıldı( \çatlamak{c_{a,\Metin{min}}}{1.5 H'_{\Metin{ef},G1}} \sağ) \sağ)
= dak sol( 1, 0.7 + 0.3 \kez kaldı( \çatlamak{8 \, \Metin{içinde}}{1.5 \zamanlar 5.6667 \, \Metin{içinde}} \sağ) \sağ) = 0.98235
\)
Çapa grubunun sentroidine gerilim yükü uygulandığından, Eksantriklik sıfırdır. Böylece, NS eksantriklik faktörü, Ayrıca maddeden 17.6.2.4.1, dır-dir:
\(
\Psi_{ec,N} = dak sol( 1.0, \çatlamak{1}{1 + \çatlamak{2 ve'_N}{3 H'_{\Metin{ef},G1}}} \sağ)
= dak sol( 1, \çatlamak{1}{1 + \çatlamak{2 \zamanlar 0}{3 \zamanlar 5.6667 \, \Metin{içinde}}} \sağ) = 1
\)
Ek olarak, her ikisi de çatlak faktörü ve bölme faktörü olarak alınır:
\(
\Psi_{c,N} = 1
\)
\(
\Psi_{cp,N} = 1
\)
Sonra, Tüm bu faktörleri birleştiriyoruz ve kullanıyoruz ACI 318-19 Eşitlik. 17.6.2.1b değerlendirmek için Çapa grubunun beton kırılma gücü:
\(
\phi N_{cbg} = Phi Sol( \çatlamak{bir_{N_C}}{bir_{N_{ortak}}} \sağ) \Psi_{ec,N} \Psi_{ed,N} \Psi_{c,N} \Psi_{cp,N} N_b
\)
\(
\phi N_{cbg} = 0.7 \kez kaldı( \çatlamak{484 \, \Metin{içinde}^ 2}{289 \, \Metin{içinde}^ 2} \sağ) \zamanlar 1 \zamanlar 0.98235 \zamanlar 1 \zamanlar 1 \zamanlar 20.475 \, \Metin{kip} = 23.58 \, \Metin{kip}
\)
NS Toplam uygulanan gerilim yükü Çapa grubunda, ayrı çapa yükünün ürünü ve ankraj sayısı:
\(
N_{Yapmak} = sol( \çatlamak{N_x}{N_{a,t}} \sağ) N_{a,G1} = sol( \çatlamak{20 \, \Metin{kip}}{4} \sağ) \zamanlar 4 = 20 \, \Metin{kip}
\)
Dan beri 20 kips < 23.58 kips , Beton kırılma kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #5: Çapa çekme kapasitesini hesaplayın
Bir çapanın çekilme kapasitesi, gömülü ucundaki direnç tarafından yönetilir. Başlamak, Gömülü plakanın yatak alanını hesaplıyoruz, Ankraj çubuğu tarafından işgal edilen alanı çıkardıktan sonra net alan.
Dikdörtgen gömülü bir plaka için, NS rulman alanı olarak hesaplanır:
\(
bir_{brg} = sol( \ayrıldı( b_{Gömme _plate} \sağ)^2 doğru) – bir_{kamış} = sol( \ayrıldı( 3 \, \Metin{içinde} \sağ)^2 doğru) – 0.44179 \, \Metin{içinde}montaj yüksekliğinde 8.5582 \, \Metin{içinde}^ 2
\)
Nerede,
\(
bir_{kamış} = frac{\pi}{4} \ayrıldı( d_a doğru)^2 = frac{\pi}{4} \kez kaldı( 0.75 \, \Metin{içinde} \sağ)montaj yüksekliğinde 0.44179 \, \Metin{içinde}^ 2
\)
Sonraki, Belirliyoruz Temel Çapa Çekme Gücü kullanma ACI 318-19 Denklem 17.6.3.2.2a.
\(
N_b = 8 bir_{brg} \ayrıldı( f’_c doğru) = 8 \zamanlar 8.5582 \, \Metin{içinde}^2 Times Sol( 4 \, \Metin{ksi} \sağ) = 273.86 \, \Metin{kip}
\)
Daha sonra uygun direnç faktörünü uyguluyoruz ve Çekme Çatlama Faktörü:
- İçin çatlak Somut, \(\Psi_{cp} = 1.0\)
- İçin çatlak Somut, \(\Psi_{cp} = 1.4\)
Bunları kullanmak, hesaplıyoruz Tasarım Çapma Çekme Mukavemeti Gerilim başına ACI 318-19 Denklem 17.6.3.1.
\(
\phi N_{pn} = Phi Psi_{c,p} N_b = 0.7 \zamanlar 1 \zamanlar 273.86 \, \Metin{kip} = 191.7 \, \Metin{kip}
\)
Daha önce hesaplananları hatırlayın Ankraj başına gerilim yükü:
\(
N_{Yapmak} = frac{N_x}{N_{a,t}} = frac{20 \, \Metin{kip}}{4} = 5 \, \Metin{kip}
\)
Dan beri 5 kips < 191.7 kips , Çapa çekme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #6: Gömme tabağı eğilme kapasitesini hesaplayın
Bu, Skyciv Base Plaka Tasarım Yazılımı Gömülü plakanın yeterli bükülme kapasitesine sahip olduğunu ve uygulanan çekme yükleri altında verilmeyeceğini doğrulamak için.
İlk, Özgürün uzunluğunu belirleriz (desteklenmeyen) gömülü plakanın ucu, desteğin kenarından çubuğun yüzüne kadar ölçüldü.
\(
b’ = frac{b_{Gömme _plate} – D_A}{2} = frac{3 \, \Metin{içinde} – 0.75 \, \Metin{içinde}}{2} = 1.125 \, \Metin{içinde}
\)
Sonraki, hesaplıyoruz bükülme anı tek tip yatak basıncı tarafından indüklenen. Bu basınç, ankraj çekme eyleminden gömülü plakaya aktarılan kuvveti temsil eder.
\(
m_f = frac{\ayrıldı( \çatlamak{T_A}{bir_{brg}} \sağ) \ayrıldı( b’ \sağ)^ 2}{2} = frac{\ayrıldı( \çatlamak{5 \, \Metin{kip}}{8.5582 \, \Metin{içinde}^ 2} \sağ) \kez kaldı( 1.125 \, \Metin{içinde} \sağ)^ 2}{2} = 0.36971 \, \Metin{kip}
\)
En sonunda, hesaplanan moment ve verilen malzeme özelliklerini kullanma, Belirleyeceğiz Minimum gerekli plaka kalınlığı direnmek bükülme verimi.
\(
t_{min} = sqrt{\çatlamak{4 M_F}{\Phi F_{Evet}}} = sqrt{\çatlamak{4 \zamanlar 0.36971 \, \Metin{kip}}{0.9 \zamanlar 36 \, \Metin{ksi}}} = 0.21364 \, \Metin{içinde}
\)
Gerçek gömülü plaka kalınlığını hatırlayın:
\(
t_{gerçek} = t_{Gömme _plate} = 0.25 \, \Metin{içinde}
\)
Dan beri 0.21364 içinde < 0.25 içinde, Gömülü plaka bükülme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #7: Y yönünde yan yüz patlama kapasitesini hesaplayın
Bu hesaplama bu örnek için geçerli değildir, belirtilen koşullar gibi ACI 318-19 Madde 17.6.4 karşılanmıyor. Bu nedenle, Y yönü boyunca yan yüz patlama hatası gerçekleşmeyecek.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #8: Z yönünde yan yüz patlama kapasitesini hesaplayın
Bu hesaplama bu örnek için geçerli değildir, belirtilen koşullar gibi ACI 318-19 Madde 17.6.4 karşılanmıyor. Bu nedenle, Z yönü boyunca yan yüz patlama hatası gerçekleşmeyecek.
Tasarım Özeti
NS Skyciv Base Plaka Tasarım Yazılımı Bu tasarım örneği için otomatik olarak adım adım hesaplama raporu oluşturabilir. Ayrıca gerçekleştirilen kontrollerin ve bunların sonuç oranlarının bir özetini sağlar, Bir bakışta bilginin anlaşılmasını kolaylaştırmak. Aşağıda bir örnek özet tablosu var, rapora dahildir.
Skyciv Örnek Raporu
SkyCiv Taban Plakası Tasarım Raporundan bekleyebileceğiniz ayrıntı ve netlik düzeyini görün. Rapor tüm önemli tasarım kontrollerini içerir, denklemler, ve sonuçların net ve okunması kolay bir formatta sunulması. Tasarım standartlarıyla tam uyumludur. SkyCiv Taban Plakası Hesaplayıcısı kullanılarak oluşturulan örnek raporu görüntülemek için aşağıya tıklayın.
Base Plaka Yazılımı Satın Alın
Base Plaka Tasarım Modülünün tam sürümünü başka bir SkyCiv modül olmadan kendi başına satın alın. Bu size taban plakası tasarımı için tam bir dizi sonuç verir, ayrıntılı raporlar ve daha fazla işlevsellik dahil.