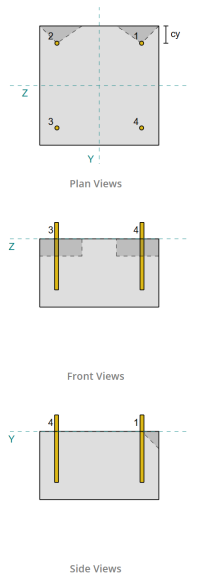
EN kullanan baz plaka tasarım örneği 1993-1-8:2005, İÇİNDE 1993-1-1:2005, İÇİNDE 1992-1-1:2004, ve EN 1992-4:2018.
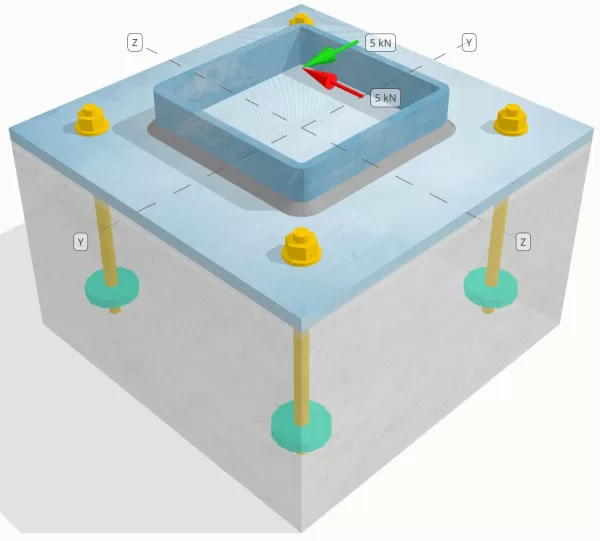
Sorun Bildirimi
Tasarlanan sütun-tabaka plaka bağlantısının bir Sen = 5-kn ve VZ = 5-KN kesme yükleri.
Verilen Veriler
Sütun:
Sütun bölümü: Shs 180x180x8
Sütun alanı: 5440 mm2
Sütun malzemesi: S235
Taban plakası:
Taban plaka boyutları: 350 mm x 350 mm
Taban plakası kalınlığı: 12 mm
Taban plaka malzemesi: S235
Izgara:
Grout kalınlığı: 6 mm
Grout Malzemesi: ≥ 30 MPa
Somut:
Somut boyutlar: 350 mm x 350 mm
Beton kalınlığı: 350 mm
Beton malzeme: C25/30
Çatlamış veya çatlaksız: Çatlak
Çapa:
Çapa: 12 mm
Etkili gömme uzunluğu: 150 mm
Gömülü plaka çapı: 60 mm
Gömülü plaka kalınlığı: 10 mm
Çapa: 8.8
Diğer bilgiler:
- Kez olmayan çapalar.
- Kesilmiş ipliklerle çapa.
- Ankraj çelik kesme arızası için K7 faktörü: 1.0
- Bağlantı elemanı kısıtlama derecesi: Kısıtlama yok
Kaynaklar:
Kaynak tipi: Fileto kaynağı
Kaynak Bacak Boyutu: 8mm
Dolgu Metal Sınıflandırması: E35
Çapa Verileri (itibaren SkyCiv Hesap Makinesi):
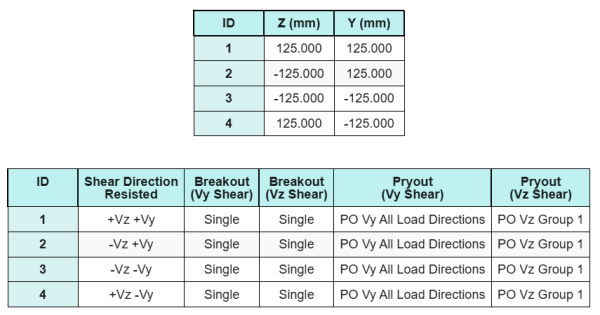
SkyCiv Ücretsiz Aracındaki Model
Ücretsiz çevrimiçi aracımızı kullanarak yukarıdaki taban plakası tasarımını bugün modelleyin! Kayıt olmanıza gerek yok.
Tanımlar
Yük yolu:
NS SkyCiv Taban Plakası Tasarım Yazılımı takip etmek İÇİNDE 1992-4:2018 Ankraj çubuğu tasarımı için. Kolona uygulanan kesme yükleri, taban plakasına kaynaklardan ve daha sonra ankraj çubuklarından destekleyici betona aktarılır. Bu örnekte sürtünme ve kesme pabuçları dikkate alınmaz, Bu mekanizmalar mevcut yazılımda desteklenmediğinden.
Çapa:
Yazılım, hangi çapaların değerlendirilmesi için bir çapa grubunun parçası olduğunu belirleyen sezgisel bir özellik içerir. beton kesme kırılması ve Beton Kesme Pryout başarısızlık.
Bir çapa örtüşen öngörülen direnç alanlarına sahip iki veya daha fazla ankraj olarak tanımlanır. Bu durumda, Çapalar birlikte hareket eder, ve birleşik dirençleri gruptaki uygulanan yüke karşı kontrol edilir.
Bir tek çapa Öngörülen direnç alanı başka biriyle örtüşmeyen bir çapa olarak tanımlanır.. Bu durumda, Çapa tek başına hareket eder, ve bu çapa üzerindeki uygulanan kesme kuvveti doğrudan bireysel direncine göre kontrol edilir.
Bu ayrım, kayma ile ilgili arıza modlarını değerlendirirken yazılımın hem grup davranışını hem de bireysel çapa performansını yakalamasını sağlar..
Adım adım hesaplamalar
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #1: Kaynak kapasitesini hesapla
Varsayıyoruz Vz Kesme yükü, Üst ve Alt Kaynaklar, iken Sen Kesme yükü, sadece sol ve sağ kaynaklar.
Kaynak kapasitesini belirlemek için Üst ve Alt Kaynaklar, Önce onların Toplam kaynak uzunlukları.
\(
L_{w,top\&alt} = 2 \ayrıldı(b_{seri} – 2t_{seri} – 2r_{seri}\sağ)
= 2 \kez kaldı(180 \,\Metin{mm} – 2 \zamanlar 8 \,\Metin{mm} – 2 \zamanlar 4 \,\Metin{mm}\sağ)
= 312 \,\Metin{mm}
\)
Sonraki, hesaplıyoruz Kaynaklardaki stresler.
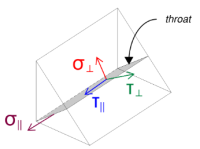
Uygulanan VZ kesme, kaynak eksenine paralel davrandığını unutmayın, başka hiçbir güç bulunmadan. Bu, dik gerilmelerin sıfır olarak alınabileceği anlamına gelir, Ve sadece Paralel yönde kesme gerilimi hesaplanması gerekiyor.
\(
\sigma_{\suçlu} = frac{N}{(L_{w,top\&alt})\,a\sqrt{2}}
= frac{0 \,\Metin{kN}}{(312 \,\Metin{mm}) \zamanlar 5.657 \,\Metin{mm} \kez sqrt{2}}
= 0
\)
\(
\sizin_{\suçlu} = frac{0}{(L_{w,top\&alt})\,a\sqrt{2}}
= frac{0 \,\Metin{kN}}{(312 \,\Metin{mm}) \zamanlar 5.657 \,\Metin{mm} \kez sqrt{2}}
= 0
\)
\(
\sizin_{\paralel} = frac{V_{ile}}{(L_{w,top\&alt})\,a}
= frac{5 \,\Metin{kN}}{(312 \,\Metin{mm}) \zamanlar 5.657 \,\Metin{mm}}
= 2.8329 \,\Metin{MPa}
\)
kullanma İÇİNDE 1993-1-8:2005, Eşitlik. 4.1, Tasarım kaynağı stresi, yön yöntemini kullanılarak elde edilir.
\(
F_{w,ED1} = sqrt{ (\sigma_{\suçlu})^ 2 + 3 \ayrıldı( (\sizin_{\suçlu})^ 2 + (\sizin_{\paralel})^2 doğru) }
= sqrt{ (0)^ 2 + 3 \kez kaldı( (0)^ 2 + (2.8329 \,\Metin{MPa})^2 doğru) }
= 4.9067 \,\Metin{MPa}
\)
Ek olarak, Base metal kontrolü için tasarım normal stresi, başına İÇİNDE 1993-1-8:2005, Eşitlik. 4.1, sıfır olarak alınır, dan beri Normal stres yok mevcut.
\(
F_{w,ED2} = sigma_{\suçlu} = 0
\)
Şimdi, Değerlendirelim sol ve sağ kaynaklar. Üst ve alt kaynaklarda olduğu gibi, Önce hesaplıyoruz Toplam kaynak uzunluğu.
\(
L_{w,left\&sağ} = 2 \ayrıldı(d_{seri} – 2t_{seri} – 2r_{seri}\sağ)
= 2 \kez kaldı(180 \,\Metin{mm} – 2 \zamanlar 8 \,\Metin{mm} – 2 \zamanlar 4 \,\Metin{mm}\sağ)
= 312 \,\Metin{mm}
\)
Daha sonra bileşenlerini hesaplarız Kaynak stresleri.
\(
\sigma_{\suçlu} = frac{N}{(L_{w,left\&sağ})\,a\sqrt{2}}
= frac{0 \,\Metin{kN}}{(312 \,\Metin{mm}) \zamanlar 5.657 \,\Metin{mm} \kez sqrt{2}}
= 0
\)
\(
\sizin_{\suçlu} = frac{0}{(L_{w,left\&sağ})\,a\sqrt{2}}
= frac{0 \,\Metin{kN}}{(312 \,\Metin{mm}) \zamanlar 5.657 \,\Metin{mm} \kez sqrt{2}}
= 0
\)
\(
\sizin_{\paralel} = frac{V_y}{(L_{w,left\&sağ})\,a}
= frac{5 \,\Metin{kN}}{(312 \,\Metin{mm}) \zamanlar 5.657 \,\Metin{mm}}
= 2.8329 \,\Metin{MPa}
\)
kullanma İÇİNDE 1993-1-8:2005, Eşitlik. 4.1, Ana metal kontrolü için hem tasarım kaynağı stresini hem de tasarım normal stresini belirliyoruz.
\(
F_{w,ED1} = sqrt{ \ayrıldı( \sigma_{\suçlu} \sağ)^ 2 + 3 \ayrıldı( \ayrıldı( \sizin_{\suçlu} \sağ)^ 2 + \ayrıldı( \sizin_{\paralel} \sağ)^2 doğru) }
\)
\(
F_{w,ED1} = sqrt{ \ayrıldı( 0 \sağ)^ 2 + 3 \kez kaldı( \ayrıldı( 0 \sağ)^ 2 + \ayrıldı( 2.8329 \,\Metin{MPa} \sağ)^2 doğru) }
\)
\(
F_{w,ED1} = 4.9067 \,\Metin{MPa}
\)
Bir sonraki adım, Hükümlü Kaynak Stresi Üst/alt kaynaklar ile sol/sağ kaynaklar arasında. Çünkü kaynak uzunlukları eşittir ve uygulanan yükler aynı büyüklüğe sahiptir, Ortaya çıkan kaynak gerilmeleri eşittir.
\(
F_{w,ED1} = \max(F_{w,ED1}, \, F_{w,ED1})
= \max(4.9067 \,\Metin{MPa}, \, 4.9067 \,\Metin{MPa})
= 4.9067 \,\Metin{MPa}
\)
Ana metal stresi sıfır kalır.
\(
F_{w,ED2} = \max(F_{w,ED2}, \, F_{w,ED2}) = \max(0, \, 0) = 0
\)
Şimdi, Kaynak kapasitesini hesaplıyoruz. İlk, Direnci dolgu kaynağı hesaplandı. Sonra, Direnci metal belirlendi. EN kullanma 1993-1-8:2005, Eşitlik. 4.1, Kapasiteler aşağıdaki gibi hesaplanır:
\(
F_{w,RD1} = frac{f_u}{\beta_w \left(\gama_{M2, yakında}\sağ)}
= frac{360 \,\Metin{MPa}}{0.8 \zamanlar (1.25)}
= 360 \,\Metin{MPa}
\)
\(
F_{w,RD2} = frac{0.9 f_u}{\gama_{M2, yakında}}
= frac{0.9 \zamanlar 360 \,\Metin{MPa}}{1.25}
= 259.2 \,\Metin{MPa}
\)
En sonunda, Kaynak gerilmelerini kaynak kapasiteleriyle karşılaştırıyoruz, ve ana metal taban metal kapasiteleri ile strese sahiptir.
Dan beri 4.9067 MPa < 360 MPa ve 0 MPa < 259.2 MPa, Kaynaklı bağlantının kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #2: VY kesme nedeniyle beton kırılma kapasitesini hesaplayın
Hükümlerini takip ederek İÇİNDE 1992-4:2018, Uygulanan yüke dik kenar, kesme kırılma arızası için değerlendirilir. Sadece Bu kenara en yakın çapalar nişanlanmış kabul edilir, Kalan ankrajların kesme direnmediği varsayılırken.
Bu kenar ankrajları, 10 · HEF ve 60 · D'den daha büyük bir beton kenar mesafesine sahip olmalıdır, nerede sahip olmak gömme uzunluğu ve d çapa çapı. Bu durum karşılanmazsa, Taban plakasının kalınlığı 0,25'ten az olmalıdır · HEF.
Eğer gereksinimler İÇİNDE 1992-4:2018, Madde 7.2.2.5(1), memnun değil, Skyciv yazılımı tasarım kontrollerine devam edemez, ve kullanıcının diğer ilgili standartlara atıfta bulunması tavsiye edilir.

Skyciv yazılım sonuçlarından, kenar çapaları gibi davranır tek çapa, Öngörülen alanları örtüşmediğinden. Bu hesaplama için, Çapa 1 düşünülecek.
Çapa ile taşınan VY kesme yükünün kısmını hesaplamak için 1, Toplam VY kesme, kenara en yakın ankrajlar arasında dağıtılır. Bu verir dikey kuvvet çapa üzerinde 1.
\(
V_{\suçlu} = frac{V_y}{N_{a,s}}
= frac{5 \,\Metin{kN}}{2}
= 2.5 \,\Metin{kN}
\)
İçin paralel kuvvet, Tüm ankrajların yüke eşit olarak direndiği varsayılmaktadır.. Bu nedenle, Yükün paralel bileşeni olarak hesaplanır.:
\(
V_{\paralel} = frac{V_Z}{N_{anc}}
= frac{5 \,\Metin{kN}}{4}
= 1.25 \,\Metin{kN}
\)
NS Toplam kesme yükü çapa üzerinde 1 bu nedenle:
\(
V_{Ed} = sqrt{ \ayrıldı( V_{\suçlu} \sağ)^ 2 + \ayrıldı( V_{\paralel} \sağ)^ 2 }
\)
\(
V_{Ed} = sqrt{ \ayrıldı( 2.5 \,\Metin{kN} \sağ)^ 2 + \ayrıldı( 1.25 \,\Metin{kN} \sağ)^ 2 } = 2.7951 \,\Metin{kN}
\)
Kapasite hesaplamasının ilk kısmı, alfa ve beta faktörleri. Kullanıyoruz İÇİNDE 1992-4:2018, Madde 7.2.2.5, ayarlamak için LF Boyutu, ve Kazıkların yüzey sürtünme direnci, kazık uzunluğu boyunca geliştirilir 7.42 ve 7.43 faktörleri belirlemek için.
\(
l_f = \min(h_{ef}, \, 12d_{anc})
= min(150 \,\Metin{mm}, \, 12 \zamanlar 12 \,\Metin{mm})
= 144 \,\Metin{mm}
\)
\(
\alfa = 0.1 \ayrıldı(\çatlamak{l_f}{c_{1,kip-ft}}\sağ)^{0.5}
= 0.1 \kez kaldı(\çatlamak{144 \,\Metin{mm}}{50 \,\Metin{mm}}\sağ)^{0.5}
= 0.16971
\)
\(
\beta = 0.1 \ayrıldı(\çatlamak{d_{anc}}{c_{1,kip-ft}}\sağ)^{0.2}
= 0.1 \kez kaldı(\çatlamak{12 \,\Metin{mm}}{50 \,\Metin{mm}}\sağ)^{0.2}
= 0.07517
\)
Bir sonraki adım hesaplamaktır. bağlantı elemanının karakteristik direncinin başlangıç değeri. kullanma İÇİNDE 1992-4:2018, Denklem 7.41, değer:
\(
V^{0}_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} = k_9 \left( \çatlamak{d_{anc}}{\Metin{mm}} \sağ)^{\Sunulan dağılım ve sonuç hesaplama yaklaşımının yalnızca dikey bir arka yüzey üzerinde hareket eden zemin basınçları için geçerli olduğunu belirtmek önemlidir.}
\ayrıldı( \çatlamak{l_f}{\Metin{mm}} \sağ)^{\beta}
\sqrt{ \çatlamak{f_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.}}{\Metin{MPa}} }
\ayrıldı( \çatlamak{c_{1,kip-ft}}{\Metin{mm}} \sağ)^{1.5} N
\)
\(
V^{0}_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} = 1.7 \kez kaldı( \çatlamak{12 \,\Metin{mm}}{1 \,\Metin{mm}} \sağ)^{0.16971}
\kez kaldı( \çatlamak{144 \,\Metin{mm}}{1 \,\Metin{mm}} \sağ)^{0.07517}
\kez sqrt{ \çatlamak{20 \,\Metin{MPa}}{1 \,\Metin{MPa}} }
\kez kaldı( \çatlamak{50 \,\Metin{mm}}{1 \,\Metin{mm}} \sağ)^{1.5}
\zamanlar 0.001 \,\Metin{kN}
\)
\(
V^{0}_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} = 5.954 \,\Metin{kN}
\)
Sonra, hesaplıyoruz Referans Yansıtılan Alan tek bir çapa, takip etme İÇİNDE 1992-4:2018, Denklem 7.44.
\(
bir_{c,V }^{0} = 4.5 \ayrıldı( c_{1,kip-ft} \sağ)^ 2
= 4.5 \kez kaldı( 50 \,\Metin{mm} \sağ)^ 2
= 11250 \,\Metin{mm}^ 2
\)
Daha sonra, hesaplıyoruz Gerçek öngörülen alan çapa 1.
\(
B_{c,V } = min(c_{ayrıldı,kip-ft}, \, 1.5c_{1,kip-ft}) + \min(c_{sağ,kip-ft}, \, 1.5c_{1,kip-ft})
\)
\(
B_{c,V } = min(300 \,\Metin{mm}, \, 1.5 \zamanlar 50 \,\Metin{mm}) + \min(50 \,\Metin{mm}, \, 1.5 \zamanlar 50 \,\Metin{mm}) = 125 \,\Metin{mm}
\)
\(
H_{c,V } = min(1.5c_{1,kip-ft}, \, t_{conc}) = min(1.5 \zamanlar 50 \,\Metin{mm}, \, 200 \,\Metin{mm}) = 75 \,\Metin{mm}
\)
\(
bir_{c,V } = H_{c,V } B_{c,V } = 75 \,\Metin{mm} \zamanlar 125 \,\Metin{mm} = 9375 \,\Metin{mm}^ 2
\)
Ayrıca kesme kırılması için parametreleri hesaplamamız gerekiyor. Kullanıyoruz İÇİNDE 1992-4:2018, Denklem 7.4, açıklayan faktörü elde etmek için Stres dağılımının bozulması, Denklem 7.46 açıklayan faktör için üye kalınlığı, ve Denklem 7.48 açıklayan faktör için Kenara eğimli bir kesme yükünün etkisi. Bunlar aşağıdaki gibi hesaplanır:
\(
\Psi_{s,V } = dak sol( 0.7 + 0.3 \ayrıldı( \çatlamak{c_{2,kip-ft}}{1.5c_{1,kip-ft}} \sağ), \, 1.0 \sağ)
= dak sol( 0.7 + 0.3 \kez kaldı( \çatlamak{50 \,\Metin{mm}}{1.5 \zamanlar 50 \,\Metin{mm}} \sağ), \, 1 \sağ)
= 0.9
\)
\(
\Psi_{h,V } = maks sol( \ayrıldı( \çatlamak{1.5c_{1,kip-ft}}{t_{conc}} \sağ)^{0.5}, \, 1 \sağ)
= maks sol( \ayrıldı( \çatlamak{1.5 \zamanlar 50 \,\Metin{mm}}{200 \,\Metin{mm}} \sağ)^{0.5}, \, 1 \sağ)
= 1
\)
\(
\alfa_{V } = tan^{-1} \ayrıldı( \çatlamak{V_{\paralel}}{V_{\suçlu}} \sağ)
= tan^{-1} \ayrıldı( \çatlamak{1.25 \,\Metin{kN}}{2.5 \,\Metin{kN}} \sağ)
= 0.46365 \,\Metin{rad}
\)
\(
\Psi_{\Sunulan dağılım ve sonuç hesaplama yaklaşımının yalnızca dikey bir arka yüzey üzerinde hareket eden zemin basınçları için geçerli olduğunu belirtmek önemlidir.,V } = maks sol(
\sqrt{ \çatlamak{1}{(\çünkü(\alfa_{V }))^ 2 + \ayrıldı( 0.5 \, (\olmadan(\alfa_{V })) \sağ)^ 2 } }, \, 1 \sağ)
\)
\(
\Psi_{\Sunulan dağılım ve sonuç hesaplama yaklaşımının yalnızca dikey bir arka yüzey üzerinde hareket eden zemin basınçları için geçerli olduğunu belirtmek önemlidir.,V } = maks sol(
\sqrt{ \çatlamak{1}{(\çünkü(0.46365 \,\Metin{rad}))^ 2 + \ayrıldı( 0.5 \times \sin(0.46365 \,\Metin{rad}) \sağ)^ 2 } }, \, 1 \sağ)
\)
\(
\Psi_{\Sunulan dağılım ve sonuç hesaplama yaklaşımının yalnızca dikey bir arka yüzey üzerinde hareket eden zemin basınçları için geçerli olduğunu belirtmek önemlidir.,V } = 1.0847
\)
Alfa faktörünü belirlerken önemli bir not, dik kesme ve paralel kesimin doğru şekilde tanımlanmasını sağlamaktır..
En sonunda, hesaplıyoruz kırılma direnci tek çapanın kullanımı İÇİNDE 1992-4:2018, Denklem 7.1.
\(
V_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} = V^0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} \ayrıldı(\çatlamak{bir_{c,V }}{A^0_{c,V }}\sağ)
\Psi_{s,V } \Psi_{h,V } \Psi_{ec,V } \Psi_{\Sunulan dağılım ve sonuç hesaplama yaklaşımının yalnızca dikey bir arka yüzey üzerinde hareket eden zemin basınçları için geçerli olduğunu belirtmek önemlidir.,V } \Psi_{= c times A_,V }
\)
\(
V_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c} = 5.954 \,\Metin{kN} \kez kaldı(\çatlamak{9375 \,\Metin{mm}^ 2}{11250 \,\Metin{mm}^ 2}\sağ)
\zamanlar 0.9 \zamanlar 1 \zamanlar 1 \zamanlar 1.0847 \zamanlar 1
= 4.8435 \,\Metin{kN}
\)
Kısmi faktörü uygulamak, Tasarım direnci 3.23 kN.
\(
V_{Yol,c} = frac{V_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c}}{\gama_{= c times A_}}
= frac{4.8435 \,\Metin{kN}}{1.5}
= 3.229 \,\Metin{kN}
\)
Dan beri 2.7951 kN < 3.229 kN, Vy kesme için kesme kırılma kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #3: VZ kesme nedeniyle beton kırılma kapasitesini hesaplayın
Aynı yaklaşım, kenardaki kapasiteyi VZ kesimine dik olarak belirlemek için kullanılır..

Simetrik tasarım nedeniyle, VZ kesme dirençli ankrajlar da tek çapa. Hadi düşünelim Çapa 1 tekrar hesaplamalar için.
hesaplamak için dik yük çapa üzerinde 1, VZ kesimini sadece kenara en yakın toplam ankraj sayısına bölüyoruz. hesaplamak için paralel yük çapa üzerinde 1, Vy kesimi toplam ankraj sayısına bölüyoruz.
\(
V_{\suçlu} = frac{V_{ile}}{N_{a,s}}
= frac{5 \,\Metin{kN}}{2}
= 2.5 \,\Metin{kN}
\)
\(
V_{\paralel} = frac{V_{Y}}{N_{anc}}
= frac{5 \,\Metin{kN}}{4}
= 1.25 \,\Metin{kN}
\)
\(
V_{Ed} = sqrt{ \ayrıldı( V_{\suçlu} \sağ)^ 2 + \ayrıldı( V_{\paralel} \sağ)^ 2 }
\)
\(
V_{Ed} = sqrt{ \ayrıldı( 2.5 \,\Metin{kN} \sağ)^ 2 + \ayrıldı( 1.25 \,\Metin{kN} \sağ)^ 2 }
= 2.7951 \,\Metin{kN}
\)
Kontrol etmek için benzer bir yaklaşım kullanmak #2, ortaya çıkan kırılma direnci VZ kesimine dik kenar için:
\(
V_{Yol,c} = frac{V_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,c}}{\gama_{= c times A_}}
= frac{4.8435 \,\Metin{kN}}{1.5}
= 3.229 \,\Metin{kN}
\)
Dan beri 2.7951 kN < 3.229 kN, VZ kesme için kesme kırılma kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #4: Beton Pryout kapasitesini hesaplayın
İçin hesaplama Kesme Pryout Direnci belirlemeyi içerir Ankrajların gerilim kırılmasına karşı nominal kapasitesi. Gerilim kırılma kapasitesi için referans İÇİNDE 1992-4:2018, Madde 7.2.1.4. Gerilim kırılmasının ayrıntılı bir tartışması zaten Gerilim yüklü Skyciv tasarım örneği ve bu tasarım örneğinde tekrarlanmayacak.
Skyciv yazılım hesaplamalarından, Gerilim kırılma bölümünün nominal kapasitesi 44.61 kN.
Sonra kullanıyoruz İÇİNDE 1992-4:2018, Denklem 7.39a, Tasarım karakteristik direncini elde etmek için. kullanma K8 = 2, Kapasite 59.48 kN.
\(
V_{Yol,cp} = frac{K_8 N_{cbg}}{\Gamma_c}
= frac{2 \zamanlar 44.608 \,\Metin{kN}}{1.5}
= 59.478 \,\Metin{kN}
\)
Kesme pryout kontrolünde, Tüm çapalar etkilidir tam kesme yüküne direnirken. Skyciv yazılımı tarafından oluşturulan görüntüden, Tüm başarısızlık koni projeksiyonları birbirleriyle örtüşüyor, çapaların bir çapa.

Bu nedenle, Ankraj grubunun gerekli direnci, sonuçta ortaya çıkan kesme yüküdür. 7.07 kN.
\(
V_{arındırma} = sqrt{(V_y)^ 2 + (V_Z)^ 2}
= sqrt{(5 \,\Metin{kN})^ 2 + (5 \,\Metin{kN})^ 2}
= 7.0711 \,\Metin{kN}
\)
\(
V_{Ed} = sol(\çatlamak{V_{arındırma}}{N_{anc}}\sağ) N_{a,G1}
= sol(\çatlamak{7.0711 \,\Metin{kN}}{4}\sağ) \zamanlar 4
= 7.0711 \,\Metin{kN}
\)
Dan beri 7.0711 kN < 59.478 kN, Kesme pryout kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #5: Ankraj çubuğu kesme kapasitesini hesaplayın
Ankraj çubuğu kesme kapasitesinin hesaplanması, kesme yükünün bir an kolu ile uygulanıp uygulanmadığına bağlıdır.. Bunu belirlemek için, Bahsediyoruz İÇİNDE 1992-4:2018, Madde 6.2.2.3, Harçın kalınlığı ve malzemesi nerede, Tasarımdaki bağlantı elemanlarının sayısı, bağlantı elemanlarının boşluğu, ve diğer faktörler kontrol edilir.
NS Skyciv Base Plaka Tasarım Yazılımı gerekli tüm kontrolleri gerçekleştirir. Kesme yükü kol kollu veya kol kolu olmadan hareket eder. Bu tasarım örneği için, Kesme yükünün değil bir kol koluyla uygulandı. Bu nedenle, kullanıyoruz İÇİNDE 1992-4:2018, Madde 7.2.2.3.1, Kapasite denklemleri için.
Çelik bağlantı elemanının karakteristik direncini hesaplayarak başlıyoruz. İÇİNDE 1992-4:2018, Denklem 7.34.
\(
V^0_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,s} = k_6 a_s f_{sen,anc}
= 0.5 \zamanlar 113.1 \,\Metin{mm}^2 Times 800 \,\Metin{MPa}
= 45.239 \,\Metin{kN}
\)
Sonraki, Faktörü için uyguluyoruz süneklik tek çapa veya çapa grubunun, alıcı K7 = 1.
\(
V_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,s} = k_7 v^{0}_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,s}
= 1 \zamanlar 45.239 \,\Metin{kN}
= 45.239 \,\Metin{kN}
\)
Sonra elde ederiz Çelik kesme arızası için kısmi faktör kullanma İÇİNDE 1992-4:2018, Tablo 4.1. Bir çapa için 8.8 malzeme, Ortaya çıkan kısmi faktör:
\(
\gama_{= c times A_,makaslama}
= maks sol( 1.0 \ayrıldı( \çatlamak{F_{sen,anc}}{F_{Y,anc}} \sağ), \, 1.25 \sağ)
= maks sol( 1 \[object Window]{800 \,\Metin{MPa}}{640 \,\Metin{MPa}}, \, 1.25 \sağ)
= 1.25
\)
Bu faktörü karakteristik dirence uygulamak, Tasarım direnci 36.19 kN.
\(
V_{Yol,s} = frac{V_{Böylece mühendisler bu hesaplamaların tam olarak nasıl yapıldığını gözden geçirebilirler.,s}}{\gama_{= c times A_,makaslama}}
= frac{45.239 \,\Metin{kN}}{1.25}
= 36.191 \,\Metin{kN}
\)
NS Gerekli kesme direnci Ankraj çubuğu, sonuçta ortaya çıkan kesme yükünün toplam ankraj çubuğu sayısına bölünmesiyle, ki hesaplanır 1.77 kN.
\(
V_{Ed} = frac{\sqrt{ (V_y)^ 2 + (V_Z)^ 2 }}{N_{anc}}
\)
\(
V_{Ed} = frac{\sqrt{ (5 \,\Metin{kN})^ 2 + (5 \,\Metin{kN})^ 2 }}{4}
= 1.7678 \,\Metin{kN}
\)
Dan beri 1.7678 kN < 36.191 kN, Ankraj çubuğu çelik kesme kapasitesi yeterli.
Soğuk şekillendirilmiş elemanlar aşağıdakilere uygun olarak tasarlanırken #6: Taban plakası taşıma kapasitesini hesaplayın
çatı yüzeyinin altındaki engel taban plakası yatak direnci kontrolü yazılımın daha sonraki bir güncellemesinde tanıtıldı. Lütfen bu bağlantıya bakın örnek hesaplama ve ayrıntılı açıklama için.
Tasarım Özeti
NS Skyciv Base Plaka Tasarım Yazılımı Bu tasarım örneği için otomatik olarak adım adım hesaplama raporu oluşturabilir. Ayrıca gerçekleştirilen kontrollerin ve bunların sonuç oranlarının bir özetini sağlar, Bir bakışta bilginin anlaşılmasını kolaylaştırmak. Aşağıda bir örnek özet tablosu var, rapora dahildir.
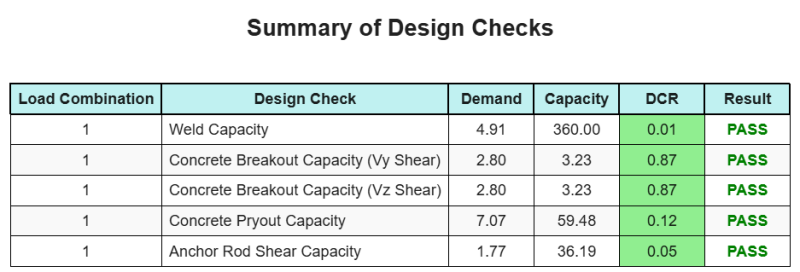
Skyciv Örnek Raporu
SkyCiv Taban Plakası Tasarım Raporundan bekleyebileceğiniz ayrıntı ve netlik düzeyini görün. Rapor tüm önemli tasarım kontrollerini içerir, denklemler, ve sonuçların net ve okunması kolay bir formatta sunulması. Tasarım standartlarıyla tam uyumludur. SkyCiv Taban Plakası Hesaplayıcısı kullanılarak oluşturulan örnek raporu görüntülemek için aşağıya tıklayın.
Base Plaka Yazılımı Satın Alın
Base Plaka Tasarım Modülünün tam sürümünü başka bir SkyCiv modül olmadan kendi başına satın alın. Bu size taban plakası tasarımı için tam bir dizi sonuç verir, ayrıntılı raporlar ve daha fazla işlevsellik dahil.